6.4А-6. Средняя скорость. Методические рекомендации к уроку

Методические рекомендации к уроку

Тема урока " Решение задач на нахождение средней скорости движения. Решение комбинаторных задач методом перебора"

Цели обучения:

6.5.1.5

решать задачи на нахождение средней скорости движения;

6.4.2.1

решать комбинаторные задачи методом перебора.

Критерии оценивания

Учащиеся

 знают:

·         как найти среднюю скорость движения;

·         как решать задачи на нахождение средней скорости движения;.

·         как решать комбинаторные задачи методом перебора;

умеют

·         определять среднюю скорость движения;

·         решать комбинаторные задачи методом перебора.

Теоретический материал

Средняя скорость вычисляется по формуле

                                    где S – путь пройденный телом

                                    t – время, за которое этот путь пройден.

Комбинаторика – раздел математики, в котором изучается, сколько различных комбинаций, подчиненных тем или иным условиям, можно составить из заданных объектов.

Решить комбинаторную задачу– это значит выписать все возможные комбинации, составленные из чисел, слов, предметов и др., отвечающих условию задачи.

Задачей комбинаторики считают  задачу размещения объектов по специальным правилам и нахождение числа способов таких размещений.

Ход урока

Организационный момент. Актуализация опорных знаний.

Проверить домашнее задание.

Совместно с учащимися определить тему и цели урока, "зону ближайшего развития".

Работа в парах. Взаимное обучение.

Создать пары из представителей разных групп. Предложить ученикам процесс взаимного обучения: объяснить напарнику ход решения задания, затем вместе решить их. Определяем умение распределять обязанности в паре.

Приложение 1

1) Какой путь проходит автобус за 4 ч, если его средняя скорость 50 км/ч?

Решение

t = 4 ч;

υ_ср = 50 км/ч;

s – ?

Средняя скорость пути υ_cp=st .

Тогда s = υ_ср·t; 50 км/ч · 4 ч = 200 км.

2) Первый участок длиной 120 м лыжник прошел за 2 мин, а второй длиной 27 м он прошел за 1,5 мин. Найдите среднюю скорость движения лыжника на всем пути.

Решение

 s₁ = 120 м; s₂ = 27 м;

t₁ = 2 мин = 120 с; t₂= 1,5 мин = 90 с;

υ_ср – ?

Средняя скорость пути υ_cp=st, где s = s₁ + s₂; t = t₁ + t₂, тогда ,

υ_ср= (120 м + 27 м)/(120 с + 90 с) = 0,7 м/с.

Ответ: 0,7 м/с.

3) Двигаясь по шоссе, велосипедист проехал 20 км за 40 мин, затем проселочную дорогу длиной 600 м он преодолел за 2 мин, а оставшиеся 39 км 400 м по шоссе он проехал за 78 мин. Чему равна средняя скорость на всем пути?

Решение

s₁ = 20 км = 20000 м; t₁ = 40 мин = 2400 с;

s₂ = 600 м; t₂ = 2 мин = 120 с;

s₃ = 39 км 400 м = 39400 м; t₃= 78 мин = 4680 с.

Тогда

υ_ср = (20000 + 600 + 39400)/(2400 + 120 + 4680) ≈ 8,3 м/с.

Ответ: 8,3 м/с.

4) Мальчик за 25 мин прошел 1,2 км, затем полчаса отдыхал, а затем пробежал еще 800 м за 5 мин. Какова была его средняя скорость на всем пути?

Решение

Средняя скорость пути υ_cp=st, где s = s₁ + s₂+ s₃; t = t₁ + t₂ + t₃; s₁ = 1,2 км = 1200 м;
t₁ = 25 мин = 1500 с; s₂ = 0 м (отдыхал); t₂ = 0,5 ч; = 1800 с; s₃ = 800 м; t₃ = 5 мин = 300 с. Тогда υ_ср = (1200 + 0 + 800)/(1500 + 1800 + 300) ≈ 0,56 м/с.

Дополнительное задание:

5)

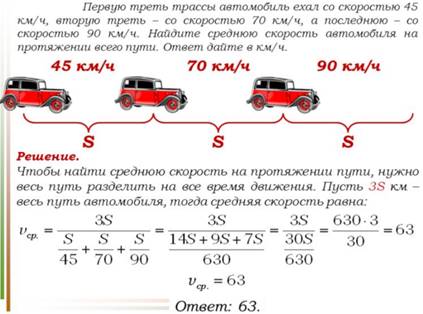
Предоставить достаточно времени для выполнения задания.

Подвести итог после решения этих заданий.

Пригласите к доске ученика, попросите его записать подробное решение задания. Учащиеся на местах решают все примеры и сверяют свои решения с записями на доске, внимательно слушают одноклассников. С целью развития математической речи попросите одного из учащихся подробно прокомментировать решение любого задания, акцентируйте их внимание на обоснование решений. Для учащихся с более высокой скоростью решения организуйте "уголок Знайки", куда они могли бы подходить и проверять свое решение или читать идею решения. Это позволяет не отвлекаться на объяснение задачи, а работать в это время с остальной частью класса.

При наличии компьютера, просмотреть презентацию для визуального закрепления материала.

Групповая работа. Объединить учащихся в разноуровневые малые группы. Раздать каждой группе карточки с заданиями.

Приложение 2

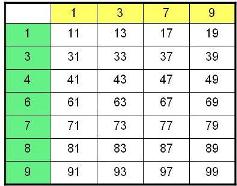
Задача 1. Сколько нечетных двузначных чисел можно составить из цифр 1, 3, 4, 6, 7, 8, 9?

Решение. Составим таблицу: слева первый столбец — первые цифры искомых чисел, вверху первая строка — вторые цифры.

Ответ: 28.

Задача 2. Для своих двух книг Маша купила три разные обложки. Сколькими различными способами она может обернуть книги купленными обложками?

Ответ: Для решения обозначим обложки буквами а, б, в. Составим из букв всевозможные пары: аб, ав, бв, ба, ва, вб. Всего получилось 6 способов.

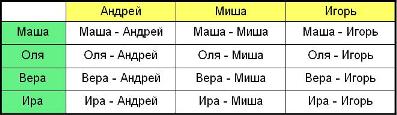
Задача 3. Маша, Оля, Вера, Ира, Андрей, Миша и Игорь готовились стать ведущими на Новогоднем празднике. Назовите возможные варианты, если ведущими могут быть только одна девочка и один мальчик.

Решение. Составим таблицу: слева первый столбец — имена девочек, вверху первая строка — имена мальчиков.

Ответ: Все возможные варианты перечисляются в строках и столбцах таблицы. Всего 12 вариантов.

Задача 4. В школьной столовой приготовили на завтрак плов (П), кашу (К), блины (Б), а из напитков – сок (С), чай (Ч) и молоко (М). сколько различных вариантов завтрака можно составить?

Ответ: 9 вариантов.

Задача 5. В кружок бального танца записались Петя, Коля, Витя, Олег, Таня, Оля, Наташа, Света. Какие танцевальные пары девочки и мальчика могут образоваться?

Ответ: 1) Таня — Петя, 2) Таня — Коля, 3) Таня — Витя, 4) Таня — Олег, 5) Оля — Петя, 6) Оля — Коля, 7) Оля — Витя, 8) Оля — Олег, 9) Наташа — Петя, 10) Наташа — Коля, 11) Наташа — Витя, 12) Наташа — Олег, 13) Света — Петя, 14) Света — Коля, 15) Света — Витя, 16) Света — Олег. А теперь рассмотрим варианты организованного перебора.

Учитель проходит по рядам, слушает, при необходимости задает дополнительные вопросы, корректирует решения учащихся, проверяет и оценивает похвалой работу групп, оказывает помощь слабоуспевающим.

Предоставить учащимся достаточно времени для выполнения заданий.

Проверить правильность ответов, провести анализ ошибок. Выслушать выводы учащихся по заданиям. Каждая группа демонстрирует свой результат выполнения заданий.

Старший группы оценивает вклад каждого, выставляя отметку.

Беседа. Рефлексия.

Вопросы учащимся:

Как найти среднюю скорость?

Что значит «решить комбинаторную задачу»?

В конце урока учащиеся проводят рефлексию, прикрепляя стикер со своим именем на слайде и или на бумаге, прикрепленной к доске.

Домашнее задание.  Знать определения, решить из уровня В учебного пособия "Математика 6" №...№.

На уроке предусмотрена дифференциация в виде работы в разнородных парах На уроке предусмотрена дифференциация в виде работы в разнородных парах (разного уровня обучаемости).

Предусмотрена взаимопроверка по ключу, в ходе которой оценивается умение учеников применять теоретические знания. В ходе групповой деятельности при выполнении задании оцениваются умение находить результат, а также решать задания по теме, опираясь на понятие и свойства, изученные на данном уроке и прошлый опыт.

Запланированы виды деятельности на уроке, способствующие передвижению учащихся по классу, поэтому необходимо обеспечить безопасность. Следить за осанкой учащихся.

Литература:

1.                  "Математика 6", Абылкасымова А.Е., Кучер Т.П., Жумагулова З.А.;

2.                  "Математика 6", Алдамуратова Т.А, Байшоланов Т.С.; Алматы. «Атамура». 2011 год.

3.                  Ершова А.П., Голобородько В.В. Самостоятельные и контрольные работы по математике для 6 класса. – 5-е изд., испр. – М.: Илекса, - 2010 – 192

4.                  Г.В.Дорофеев, Л.Г. Петерсон. Математика. 6 класс. Часть 3. Москва. Ювента. 2011 год.

5.                  Математика - 6» автор Н.Я.Виленкин, Жохов В.И, Чесноков А.С. и др., Москва «Мнемозина», 2010г.

Интернет ресурсы:

1.                  http://www.yaklass.ru

2.                  https://school-assistant.ru

3.