АБСОЛЮТНАЯ ПОГРЕШНОСТЬ

Абсолютная погрешность
приближенного значения

Цели: ввести понятие абсолютной погрешности приближенного значения; формировать умение находить абсолютную погрешность приближенного значения и значение величины по точности её измерения.

Ход урока

I. Организационный момент.

II. Проверочная работа.

В а р и а н т  1

1. Пусть 2 < a < 3 и 1 < b < 2. Оцените значение выражения:

а) a + b;           б) a – b;           в) ab;           г) .

2. Зная, что  1,7 <  < 1,8  и  2,4 <  < 2,5, оцените значение выражения:

а) +;           б) –.

В а р и а н т  2

1. Известно, что 5 < х < 6 и 2 < у < 3. Оцените значение выражения:

а) х + у;           б) х – у;           в) ху;           г) .

2. Зная, что  1,4 <  < 1,5  и  2,2 <  < 2,3, оцените значение выражения:

а) +;           б) –.

В а р и а н т  3

1. Известно, что 8 <a < 10 и 1 < b < 2. Оцените значение выражения:

а) a + b;           б) a – b;           в) ab;           г) .

2. Зная, что  2,4 <  < 2,5  и  3,1 <  < 3,2, оцените значение выражения:

а) +;           б) –.

III. Устная работа.

1. Округлите число:

а) 35,7 до единиц;                                г) 0,53748 до тысячных;

б) 289 до десятков;                              д) 3847,5 до сотен;

в) 82,3591 до десятых;            е) 1,384795 до десятитысячных.

2. a < b и b 0, найдите значение выражения:

а) | a + b | = *;                             в) | b – a | = *;

б) | a | + | b | = *;             г) | a ∙  b | = *.

3. Представьте в виде десятичной дроби.

а) ;           б) ;           в) ;           г) .

IV. Объяснение нового материала.

1. М о т и в а ц и я   и з у ч е н и я.

Многочисленные приложения математических методов в различных областях знаний и жизненной практике часто осуществляются в форме решения задач на вычисление. Значения таких непрерывных величин как расстояние, скорость, стоимость, сила тока и др. обязательно являются приближенными числами, так как точные измерения таких величин принципиально невозможны. Это связано с особенностями как самих измерительных приборов, так и с погрешностями, которые допускает человек, пользующийся этими приборами.

Практическое использование полученного приближенного числа без оценки его погрешности может оказаться опасным. Например, изготовление хотя бы одной детали самолёта по расчётным данным, точность которых неизвестна, может обернуться катастрофой.

2. В в е д е н и е   п о н я т и я  абсолютной погрешности.

Объяснение проводить в соответствии с пунктом учебника. На доску выносится запись:

Обращаем внимание учащихся, что абсолютная погрешность показывает разницу между точным и приближённым значением в абсолютном выражении, не указывая, в какую сторону ошиблись при вычислении – увеличения или уменьшения числа.

3. Для первичного закрепления понятия абсолютной погрешности выполним упражнения из учебника № 782 и № 783 (а, б).

Р е ш е н и е

№ 782.

1) 17,26 ≈ 17,3.

Абсолютная погрешность равна | 17,26 – 17,3 | = | –0,04 | = 0,04.

2) 12,034 ≈ 12,0.

Абсолютная погрешность равна | 12,034 – 12,0 | = | 0,034 | = 0,034.

3) 8,654 ≈ 8,7.

Абсолютная погрешность равна | 8,654 – 8,7 | = | –0,046 | = 0,046.

№ 783.

а) 9,87 ≈ 10.

Абсолютная погрешность равна | 9,87 – 10 | = | –0,13 | = 0,13.

б) 124 ≈ 120.

Абсолютная погрешность равна | 124 – 120 | = | 4 | = 4.

4. Рассматриваем случаи, когда абсолютную погрешность найти невозможно (мы не знаем точного значения). В подобных ситуациях мы указываем число, больше которого абсолютная погрешность быть не может.

Вообще, если х ≈ а и абсолютная погрешность этого приближённого значения не превосходит некоторого числа h, то число а называют приближённым значением х с точностью до h.

На доску выносим соответствующую запись:

или

Просим  ребят  привести  примеры,  где  они  встречали  подобную  запись  (надпись  на  рулоне  обоев:  18 ± 0,3 м;  надпись  на  коробке  с конфетами:  300 ± 5 г;  надпись  на  упаковке  с  замороженными  продуктами: –20 ± 2 °С).

V. Формирование умений и навыков.

1. № 784, № 785 (а).

Р е ш е н и е

№ 784.

 ≈ 0,14. Абсолютная погрешность равна

.

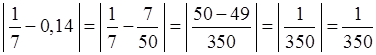№ 785 (а).

у = 6,5 ± 0,1, значит, 6,5 – 0,1 ≤ у ≤ 6,5 + 0,1;

6,4 ≤ у ≤ 6,6.

2. Представьте обыкновенную дробь в виде десятичной и округлите до тысячных. Найдите абсолютную погрешность приближения:

а) ;          б) 1.

Р е ш е н и е

а)  = 0,8(3) = 0,83333... ≈ 0,833. Абсолютная погрешность равна

.

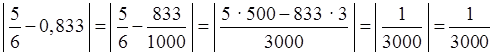б) 1 =  = 1,(45) = 1,4545... ≈ 1,455.

Абсолютная погрешность равна

.

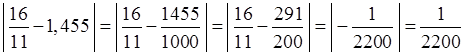3. № 787, № 789.

Р е ш е н и е

№ 787.

а = 420 г ± 3 %, значит, 420 – 3 % ≤ а ≤ 420 + 3 %.

 ∙  3 = 12,6; 420 – 12,6 ≤ а ≤ 420 + 12,6;

407,4 ≤ а ≤ 432,6.

О т в е т: 407,4 ≤ а ≤ 432,6.

№ 789.

Масса мешка картофеля равна  32 ± 1 кг,  то есть  32 – 1 ≤ т ≤ 32 + 1;
31 ≤ т ≤ 33.

Пусть а – приближённое значение массы мешка картофеля с точностью до 0,1 кг, тогда

а – 0,1 ≤ т ≤ а + 0,1.

а) Если а = 31,4, то 31,3 ≤ т ≤ 31,5.

31,3 > 31   и   31,5 < 33, значит, масса может оказаться равной 31,4 кг.

б) Если а = 32,5, то 32,4 ≤ т ≤ 32,6.

32,4 > 31   и   32,6 < 33, значит, масса может оказаться равной 32,5 кг.

в) Если а = 33,2, то 33,1 ≤ т ≤ 33,3.

33,1 > 33, значит, масса не может оказаться равной 33,2 кг.

г) Если а = 30,7, то 30,6 ≤ т ≤ 30,8.

30,8 < 31, значит, масса не может оказаться равной 30,7 кг.

О т в е т: а) Да. б) Да. в) Нет. г) Нет.

VI. Итоги урока.

В о п р о с ы   у ч а щ и м с я:

– Сформулируйте правило округления чисел.

– Что называют абсолютной погрешностью приближенного значения?

– Объясните смысл записи х = а ± h.

– От чего зависит точность приближённого значения?

Домашнее задание: № 783 (в, г), № 785 (б), № 786, № 788.