
1. Заново прочитать условие задачи.
2. Найти в нем слова-ключи и подчеркнуть их.
3. На основе слов-ключей и физических законов сформулировать обоснование.
P.S. Слова-ключи – это подсказки от авторов, наводящие на решение задачи.
Пример:
На горизонтальной поверхности неподвижно закреплена абсолютно гладкая полусфера радиусом R = 2,5 м. С её верхней точки из состояния покоя соскальзывает маленькое тело. В некоторой точке тело отрывается от сферы и летит свободно. Найдите скорость тела в момент отрыва от сферы. Сопротивлением воздуха пренебречь. Обоснуйте применимость используемых законов к решению задачи.
Найденные слова-ключи: абсолютно гладкая поверхность, из состояния покоя, маленькое тело, отрыв, свободное падение, сопротивления воздуха нет.
Теперь на основе найденных слов-ключей сформулируем обоснование:
1. Рассмотрим задачу в системе отсчёта, связанной с Землёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Так как по условию задачи дано маленькое тело, то его можно рассматривать как материальную точку.
3. Тело начинает движение из состояния покоя, значит его начальная скорость равна 0.
4. Сопротивлением воздуха можно пренебречь, а сфера имеет абсолютно гладкую поверхность, следовательно трения при движении тела по сфере нет, поэтому его механическая энергия при движении по поверхности сферы сохраняется. (Силы сопротивления и трения не вводим, записываем ЗСЭ).
5. Поскольку тело описывается моделью материальной точки, условие его отрыва от поверхности сферы 2-м законом Ньютона. В момент отрыва сила реакции опоры N = 0. (отрыв => сила реакции опоры в момент отрыва N=0).
Мы видим, что каждому слову-ключу соответствует определенный пункт в обосновании к решению данной задачи. Таким образом, обоснование формируется путем анализа слов-ключей, найденных в тексте условия, и законов, применяемых для решения данной задачи.
Лайфхак: Зачастую проще сначала решить задачу на черновике. Глядя на использованные при решении законы и формулы, распознать слова-ключи в условии становится намного легче. Поэтому рекомендуется сначала решить задачу на черновике и только потом начинать писать обоснование.
Важно:
1. Чтобы ваше решение всей задачи выглядело красиво и логично, на «беловик» (листы КИМ) переписывается сначала обоснование, а потом уже текст решения, как это и было сделано в авторском примере, приведённом выше.
2. Приведённые слова-ключи не всегда встречаются в тексте условий задач в том виде, в котором они приведены в данном пособии. Приведённые слова отражают лишь общий смысл фраз, которые нужно искать.
3. Например, существуют следующие аналоги слова-ключа «гладкая поверхность»: абсолютно гладкое тело, коэффициент трения отсутствует / пренебрежимо мал, трения нет, потери на трение пренебрежимо малы.
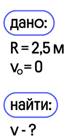
Обоснование
1. Рассмотрим задачу в системе отсчёта, связанной с 3емлёй. Будем считать эту систему отсчёта инерциальной (ИСО).
2. Так как по условию задачи дано маленькое тело, то его можно рассматривать как материальную точку.
3. Тело начинает движение из состояния покоя, значит его начальная скорость равна 0.
4. Сопротивлением воздуха можно пренебречь, а сфера имеет абсолютно гладкую поверхность, следовательно трения при движении тела по сфере нет, поэтому его механическая энергия при движении по поверхности сферы сохраняется. (Силы сопротивления и трения не вводим, записываем ЗСЭ).
5. Поскольку мы имеем дело с моделью материальной точки, условие его отрыва от поверхности сферы описывается вторым законом Ньютона. В момент отрыва сила реакции опоры N = 0. (Отрыв -> сила реакции опоры в момент отрыва N = 0).
Решение
1. Запишем закон сохранения энергии для двух состояний тела (на вершине сферы и в момент отрыва):

где m – масса тела, v – скорость тела в момент отрыва.
1. Запишем в точке отрыва второй закон Ньютона в проекциях на ось x:
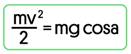
1. Используя (1), (2) и условие
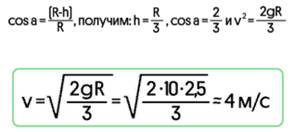
Ответ: ≃ 4 м/с.
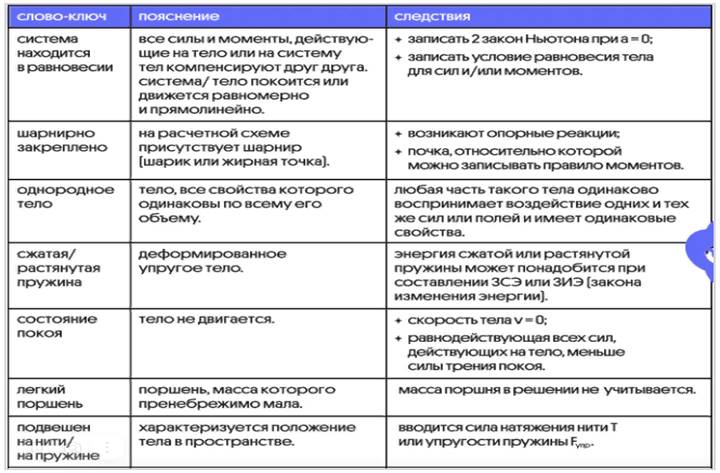
Перечень слов-ключей
Важно: существует огромное число вариаций задач и совокупностей условий, поэтому в данной таблице приведены только самые основные следствия, на которые указывают слова-ключи.
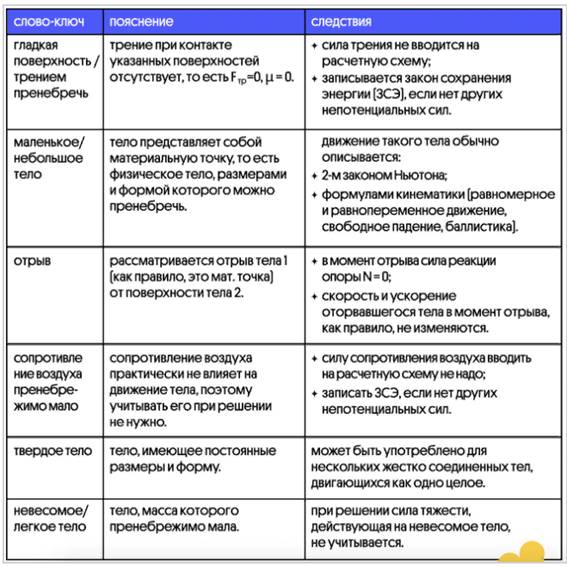

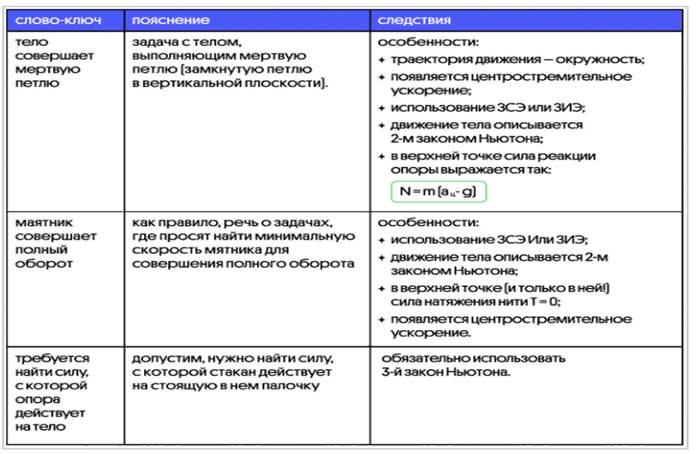
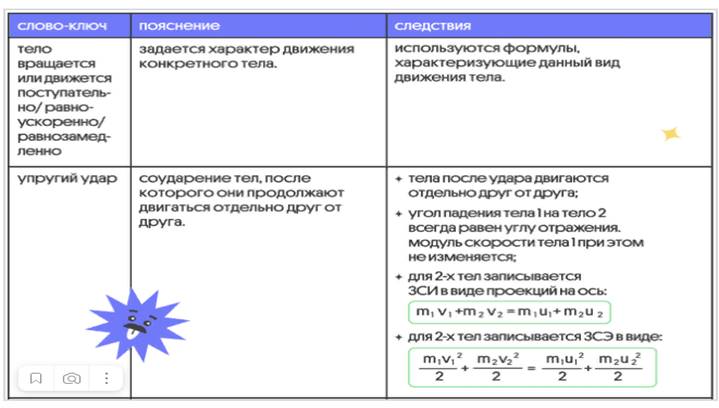

Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.