Алгоритм работы с дробями

Эталоны

А₁  Алгоритм сложения смешанных чисел:

Ш. 1: привести дробные части к наименьшему общему знаменателю (найти НОК знаменателей дробных частей);

Ш. 2: выполнить отдельно сложение целых частей и сложение дробных частей;

Ш. 3: если дробная часть суммы окажется сократимой дробью, то сократить эту дробь;

Ш. 4: если дробная часть суммы окажется неправильной дробью, то выделить из нее целую часть и прибавить к целой части суммы.

А₂ Алгоритм вычитания смешанных чисел:

Ш. 1: привести дробные части к наименьшему общему знаменателю (найти НОК знаменателей дробных частей);

Ш. 2: если дробная часть уменьшаемого меньше дробной части вычитаемого, «занять» единицу из целой части;

Ш. 3: отдельно вычесть целые части и дробные части;

Ш. 4: если дробная часть разности окажется сократимой дробью, то сократить эту дробь.

Чтобы записать смешанное число в виде неправильной дроби:

1) знаменатель умножить на целую часть;

2) к произведению прибавить числитель дробной части;

3) полученную сумму записать в числитель, а знаменатель оставить без изменения.

Чтобы преобразовать неправильную дробь в смешанное число, числитель делят на знаменатель с остатком: частное даёт целую часть, остаток – числитель, а делитель – знаменатель дробной части.

А₃ Алгоритм умножения дробей

Ш.1: Произведение дробей записать в виде дроби, в числители,  которой записано произведение числителей, в знаменателе произведение знаменателей.

Ш.2: Если возможно сократить, получившуюся дробь.

Ш.3: Найти произведение чисел, стоящих в числителе и чисел, стоящих в знаменателе.

Ш.4:  Если получилась неправильная дробь, выделить целую часть.

А₄ Алгоритм умножения дроби на натуральное число

Ш.1: Записать дробь: в числители произведение числителя дроби и натурального числа, в знаменателе старый знаменатель.

Ш.2: Если возможно сократить, получившуюся дробь.

Ш.3: Найти произведение чисел в числителе.

Ш.4: Если результат неправильная дробь, выделить целую часть.

, a; b; n Î N.

А₅ Алгоритм умножения смешанных чисел:

Ш.1: Смешанные числа представить в виде не правильных дробей.

Ш.2: Перемножить, получившиеся дроби по известному алгоритму умножения дробей.

Ш.3: Если получилась неправильная дробь, выделить целую часть.

А₆ Алгоритм умножения смешанного числа на натуральное число

Ш.1: Умножить целую часть на натуральное число.

Ш.2: Умножить дробную часть на натуральное число.

Ш.3: Найти сумму результатов первого и второго шага.

А₇  Алгоритм деления дробей

Ш.1:  Деление заменить умножением.

Ш.2:  Делитель заменить числом, обратным.

Ш.3: Выполнить умножение по известному алгоритму: .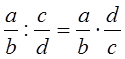

Первый алгоритм деление дроби на натуральное число

Ш.1: Заменить деление умножением.

Ш.2: Натуральное число заменить дробью с числителем 1.

Ш.3: Выполнить умножение по известному алгоритму.

Второй алгоритм деление дроби на натуральное число

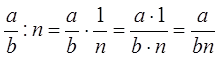
Ш.1: В частном записать дробь.

Ш.2: Числитель оставить без изменения.

Ш.3: В знаменателе записать произведение знаменателя дроби и натурального числа.

Ш.4: Сократить если возможно дробь.

Ш.5: Выделить целую часть, если дробь не правильная.

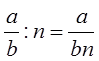
А₈: Алгоритм деления смешанных чисел

Ш.1: Перевести смешанные числа в неправильные дроби.

Ш.2: Выполнить деление по известному алгоритму деления дробей.

Первый алгоритм деления смешанных чисел на натуральное число

1. Перевести смешанное число в неправильную дробь.

2. Выполнить деление дроби на натуральное число.

Второй алгоритм деления смешанных чисел на натуральное число

1. Разделить целую часть на натуральное число.

2. Разделить дробную часть на натуральное число по алгоритму деления дроби на натуральное число.

3. Найти сумму, получившихся результатов.

Алгоритм решения задач на дроби

1. Прочти задачу.

2. Составить схему к условию задачи.

3. Запишите формулу.

4. Поставить в формулу значения переменных из условия задачи.

5. Найдите значение неизвестной переменной.

6. Ответить на вопрос задачи.

Алгоритм решения задачи

1 способ:                                                           2 способ:

1. Построить схему;                                     1. Построить схему;

2. Найти часть от числа,

 выраженную дробью;                                  2. Найти, какая часть приходится на остаток;

3. Найти остаток от числа.                       3. Найти часть от числа, выраженную дробью.