Асимптоты дробно-рациональных функций

 

 

 

 

 

 

 

 

 

 

 

 

«Асимптоты  дробно-рациональных функций»

 

 

 

 

 

 

Секция: математика

 

 

 

 

           

Автор:

 

Мантрова Марина Николаевна,

учитель математики МБУ «Школа № 11»

г.о. Тольятти Самарской обл.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Тольятти 2022

СОДЕРЖАНИЕ.

Введение…………………………………………………………………………...3

Раздел 1. Теоретические сведения об асимптотах……………………...............5

1.     Понятие асимптоты………………………………………….……………..5

2.     Виды асимптот графиков………………………………………………….5

3.     Связь между наклонной и горизонтальной асимптотами……………….6

4.     Правила нахождения асимптот…………………………………................7

Раздел 2. Образцы дробно-рациональных функций, при построении графиков которых асимптотами являются параболы и гиперболы………………….…..10

1.     Задача № 1405, Берман…………………………………………………...10

2.     Задача № 1215, Минорский………………………………………………11

3.     Задача № 1217, Минорский………………………………………………13

4.     Задача №1400, Берман……………………………………………………15

5.     Задача №5………………………………………………………………...17

Выводы…………………………………………………………………………...20

Литература……………………………………………………………………….21

 

 

 

 

 

 

 

ВВЕДЕНИЕ.

Графики функций являются неотъемлемой частью школьного курса математики. От точности их построения зависит, насколько правильно будут определены свойства тех или иных функций. Для более точного построения графиков необходимо выявить наличие у них асимптот.

Цель работы -  выяснить, могут ли графики дробно-рациональных функций асимптотически приближаться к кривым: параболам и гиперболам.

           Для достижения цели исследования  поставлены конкретные задачи:

1.     Изучить состояние вопроса по источникам информации.

2.     Выдвинуть гипотезу о том, что в качестве асимптот могут выступать параболы и гиперболы.

3.     Экспериментально проверить свою гипотезу в процессе построения графиков.

          При решении сформулированных задач были использованы следующие методы: изучение и анализ литературы по проблеме исследования, наблюдение, синтез, индукция.

          Объектом исследования являются графики дробно-рациональных функций.

          Предмет исследования: асимптоты.

         

         

 

 

РАЗДЕЛ 1. ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ ОБ АСИМПТОТАХ.

1.     Понятие асимптоты.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении этой точки по кривой от начала координат или, что то же, когда расстояние точки от начала координат неограниченно растет. [1, с 238]

2.     Виды асимптот графиков.

Вертикальная

Вертикальная асимптота — прямая вида   при условии существования предела .

Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Итак, для того, чтобы ветвь кривой у=f(х) имела вертикальную асимптоту х=а, необходимо и достаточно, чтобы выполнялось одно из соотношений:

. [2,c.391]

Горизонтальная

Горизонтальная асимптота — прямая вида   при условии существования предела

.

Наклонная

Наклонная асимптота — асимптота, не перпендикулярная оси Ох. Уравнение этой асимптоты должно иметь вид    . [2, с.392]

 Если существуют конечные пределы  

    , ,

 то кривая  у=f(х)  имеет асимптоту . [1, с. 239]

Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот!

Замечание: Если хотя бы один из двух упомянутых выше пределов не существует (или равен ), то наклонной асимптоты при (или ) не существует!

3.     Связь между наклонной и горизонтальной асимптотами

Если при вычислении предела , то очевидно, что наклонная асимптота совпадает с горизонтальной. Какова же связь между этими двумя видами асимптот?

Дело в том, что горизонтальная асимптота является частным случаем наклонной при , и из выше указанных замечаний следует, что

А.   Функция имеет или только одну наклонную асимптоту, или одну горизонтальную асимптоту, или одну наклонную и одну горизонтальную, или две наклонных, или две горизонтальных, либо же вовсе не имеет асимптот.

Б.     Существование указанных в п. А. асимптот напрямую связано с существованием соответствующих пределов. 

 

 

 

 

 

4.     Правила нахождения асимптот.

Алгоритм нахождения асимптот через пределы:

1.     Нахождение вертикальных асимптот.

2.     Нахождение двух пределов

3.     Нахождение двух пределов

если   в п. 2., то , и предел  ищется по формуле горизонтальной асимптоты,

Наклонная асимптота может быть получена также путем выделения целой части из рациональной дроби [3, с.240]. Для кривой у=Р(х)/G(х) существует наклонная асимптота при условии, что степень многочлена Р(х) на единицу больше степени многочлена G(х) [3, с.240].

Рассмотрим конкретный пример: Задача №1409, Берман[4,]

Построить график функции у=.

Преобразуем функцию к виду у= и выделим из неё целую часть  

=, где целая часть   и есть наклонная асимптота.

Можно было её найти  и через пределы.

 

У=кх+b,  у=    - наклонная асимптота.

Проведём полное исследование функции для построения её графика.

D(у)=, следовательно х=-1 вертикальная асимптота.

,  при  х=0, х=-1, х=-3.

х		-3		-1		0
У				Не сущ.		0
	+	0	-	не сущ.	+	0	+
		Точка максимума		Точка разрыва		Точка перегиба

 

Дополнительные точки:

х	-2	-0,5	1	2
у	-4	-0,25

 

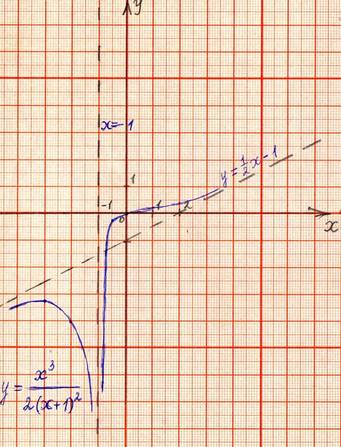Таблица для наклонной асимптоты у=:

х	4	0
у	1	-1

 

Используя исследование функции, строим её график.

 

 

 

 

 

 

Рассмотренный выше пример показывает, как искать наклонные асимптоты для графиков дробно-рациональных функций: надо представить, если это возможно, данную функцию в виде суммы линейной функции и функции, бесконечно малой при х→∞. Тогда график линейной функции и будет наклонной асимптотой. Из разобранного примера видно, что наклонная асимптота к графику рациональной функции существует, если степень числителя на единицу больше степени знаменателя.[3, c.137 – 138]

Изучая учебное пособие для углубленного изучения математики Виленкина Н. Я. « Алгебра и математический анализ для 10 класса» [3],  я нашла задание № 300, в котором говорится найти параболу, к которой неограниченно приближаются при х→∞ графики следующих: функций: [3]

У меня возник вопрос, а что будет, если степень числителя на 2 или 3 единицы больше знаменателя, или на 1,2 единицы меньше степени знаменателя? Ответа на свой вопрос в книжных источниках и интернете найти не удалось.  После анализа сборников задач по высшей математике [4],  [5] я нашла ряд функций, которые меня заинтересовали. Например,

 у=,  у=, у=, у=.  Более подробно рассмотрим эти функции в следующем разделе и попробуем к ним применить метод выделения целой части для нахождения криволинейных асимптот.

 

 

РАЗДЕЛ 2. ОБРАЗЦЫ ДРОБНО-РАЦИОНАЛЬНЫХ ФУНКЦИЙ, ПРИ ПОСТРОЕНИИ ГРАФИКОВ КОТОРЫХ АСИМПТОТАМИ ЯВЛЯЮТСЯ ПАРАБОЛЫ И ГИПЕРБОЛЫ.

1.     Задача № 1405, Берман. [4]

Построить график функции  у= .

 По аналогии с рассмотренным выше примером выделим целую часть из дроби . Можно предположить, что  - это асимптота, но явно, что это не линейная функция, а квадратичная. Проверим, действительно ли это так экспериментальным путём.  Построим график функции, опираясь на её исследование, и график предполагаемой асимптоты.

D(у)= , поэтому х=0 – вертикальная асимптота.

==0,    если   х=0,5.

=0, если   х=0,  х=.

 

х				0		0,5
у		0		Не сущ.		3
	-		-	Не сущ.	-	0	+
	+	0	-	Не сущ.	+		+
		Точка перегиба		Точка разрыва		Точка минимума

 

Дополнительные точки:

Х	1	2	-1
у	5	16,5	3

 

Таблица для асимптоты у=:

Х	-2	-1	0	1	2
у	16	4	0	4	16

 

На основании исследования функции строим её график и её асимптоты.

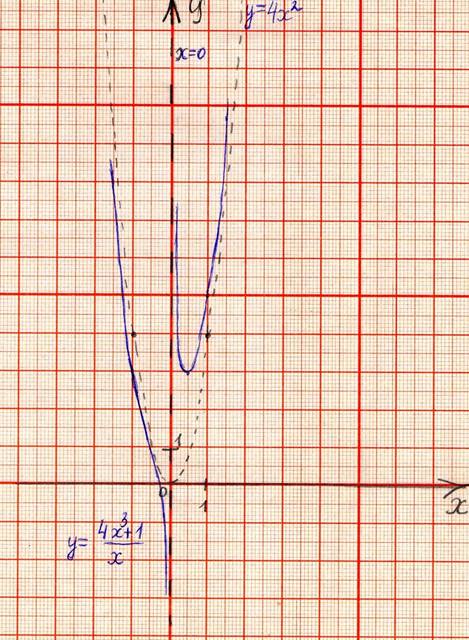
Вывод: очевидно, что график функции у= действительно приближается к квадратичной параболе у=4х²

2.     Задача № 1215, Минорский. [5]

Построить график функции у= . 

Преобразуем функцию к виду у=  и выделим из дроби целую часть .

Предположим, что целая часть  - это параболическая асимптота данного графика. Убедимся в этом на практике.

D(у)= , значит х=2 – вертикальная асимптота.

=0,  если х=1 и х=4.

Х		1		2		4
У		3		Не сущ.		0
	-	0	+	Не сущ.	+	0	+
		Точка минимума		Точка разрыва		Точка перегиба

 

Дополнительные точки:

Х	0	1	3	4	5	6
у		3	-	0

 

Таблица для параболической асимптоты   у= :

Вершина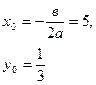

х	3	4	5	6
у

 

Используя результаты исследования функции,  строим её график и  асимптоты.

Вывод: убеждаемся, что у= квадратичная парабола является асимптотой для графика функции у=

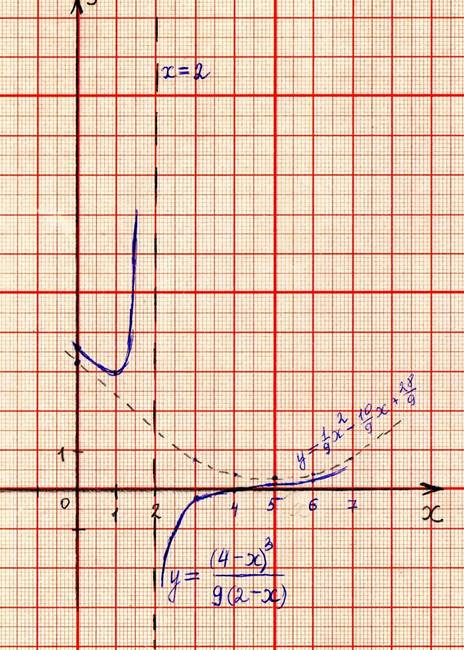
3.     Задача № 1217, Минорский. [5]

Построить график функции У=.

Преобразуем функцию к виду у =  .  Предположим, что

  у= гиперболическая асимптота. Проверим это, выполнив построения.

D(у)=. Следовательно, х=0 – вертикальная асимптота.

Найдём  к=

               b=

Значит, у=0 = горизонтальная асимптота.

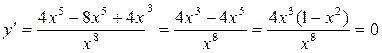,  если х=1,  х= -1, х=0.

Вычислим

х		-1		0		1
у		1		Не сущ.		1
	+	0	-	Не сущ.	+	0	-
		Точка максимума		Точка разрыва		Точка максимума

 

Дополнительные точки:

Х	1	2	3	0,5
у	1			-8

 

Таблица для асимптоты  у=

Х	1	2	3	0,5
у	2	0,5		8

 

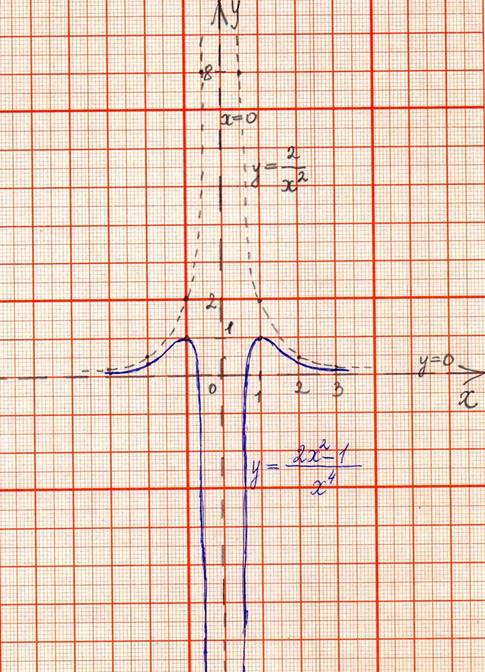
Вывод: график функции у= имеет гиперболическую асимптоту у=

4.     Задача №1400, Берман. [4]

Провести полное исследование данной функции и начертить её график

У= .

Приведём данную функцию к виду у= .

Можно предположить, что у=  является криволинейной асимптотой для данного графика. Проверим это экспериментальным путём, сделав полное исследование функции, построив её график и асимптоту у= .

D(у)= , следовательно х=1 и х=-1 – вертикальные асимптоты.

Найдём к=,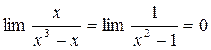

              в= .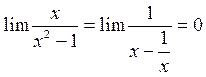

У=0 – горизонтальная асимптота.

Вычислим 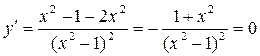 ни при каких значения х.

Х		-1		1
У		Не сущ.		Не сущ.
	-	Не сущ.	-	Не сущ.	-
		Точка разрыва		Точка разрыва

 

Дополнительные точки для построения данного графика:

Х	0	0,5	1,5	2	2,5	3
у	0	-	1,2		0,48	0,375

 

Таблица для построения асимптоты:

Х	0,5	1	1,5	2
у	2	1		0,5

 

Основываясь на исследовании, построим график функции.

 

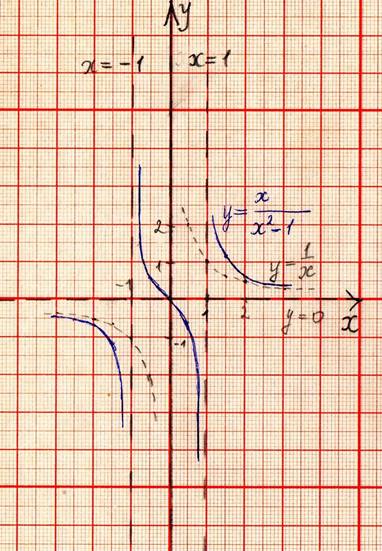
Вывод: кривая у=(гипербола) служит асимптотой для графика функции у=.

5.  Задача 5.  Попробую сама взять дробно – рациональную функцию, у которой степень числителя на 3 единицы больше степени знаменателя .

 Найдём асимптоту путём выделения целой  части.. Значит, g(x)= - асимптота.

Таблица точек для построения асимптоты:

Х	0	1	2	3	-1	-2
у	-1	0	5	20	-4	-15

 

Проведём исследование функции при помощи аппарата производной.

     при х=0 и х=-.

Х				-1		0
	+	0	-	Не сущ.	-	0	+
у		-9,5		Не сущ.		0
		Точка максимума		Точка разрыва		Точка минимума

 

Дополнительные  точки для построения функции  :

х	-2	-1,5	-0,5	0,5	1	2
у	-16	-10,1	-0,125	0,04	0,5	5,3

 

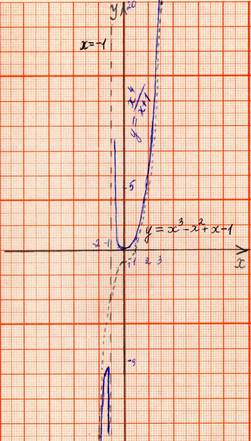
Вывод: график функции   приближается к кубической асимптоте  g(x)=.

ВЫВОДЫ.

       Таким образом, на основании проделанной работы мною были сделаны следующие выводы:

1.     Графики дробно рациональных функций могут иметь не только асимптоты, представленные линейной функцией, но и кривые линии, к которым они асимптотически приближаются: квадратичную, кубическую параболы, а также гиперболы.

2.     Если степень многочлена числителя больше степени многочлена знаменателя на 2 единицы, то асимптотой будет квадратичная парабола, если разность степеней равна 3 единицам, то асимптотой будет кубическая парабола. Логически можно предположить, что если разница между степенью многочлена числителя больше степени многочлена знаменателя на четное число единиц, то асимптотой будет квадратичная парабола, ветви которой ближе к оси ординат; если же эта разность составляет нечетное число, например 5, 7, 9, то асимптотой будет парабола вида кубической, ветви которой приближены к оси ординат.

3.     Если степень многочлена числителя меньше степени многочлена знаменателя на 1(также все нечетные числа) единицу, то асимптотой будет нечётная гипербола, а если степень знаменателя на 2 (все четные числа) единицы больше степени числителя, то асимптотой будет чётная гипербола.

4.     Знание криволинейных асимптотических линий  необходимо тогда, когда дробная рациональная функция не имеет прямолинейных асимптот. Криволинейные асимптотические линии позволяют точнее построить график той или иной функции.

 

 

ЛИТЕРАТУРА.

1.     Игнатьева А. В. и др. Курс высшей математики /А. В. Игнатьева, Т. И. Краснощекова, В. Ф. Смирнов; Под редакцией П.И.Романовского. – 2-е изд. – М.: «Высшая школа», 1968. - 670с.

2.     Уваренков И.М., Малер М.З. Курс  математического анализа. - Том 1. -  М.: «Просвещение», 1966. - 640с.

3.     Виленкин Н. Я. и др. Алгебра и математический анализ для 10 класса: Учеб. пособие для учащихся школ и классов с углубл. изуч. математики / Н.Я.Виленкин, О.С.Ивашев–Мусатов, С.И. Шварцбурд. – 4-е изд. - М.: «Просвещение», 1995. - 335с.

4.     Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие для высш. учеб. заведений. - 17-е изд. – М.: «Наука», 1972. -  412с.

5.     Минорский В.П. Сборник задач по высшей математике: Учеб. пособие для студ. высш. технич. учеб. заведений – 12-е изд., стереотип. -  М.: «Наука», 1978. -  352с.