Автоматизированный морфометрический анализ рельефа

Тема 3. Автоматизированный морфометрический анализ рельефа

3.1. Теоретические основы морфометрии рельефа

Морфометрия - научное направление геоморфологии, исследует количественные (геометрические) свойства рельефа земной поверхности с целью их выявления и описания; своими методами она способствует изучению происхождения и истории развития рельефа, создает морфологические основания, необходимые для познания основных закономерностей формирования и развития рельефа земной поверхности.

Для этих целей она использует любую количественную информацию о рельефе изучаемой территории. Это могут быть не только результаты картометрических работ, но и данные профилирования территории (нивелирные ходы, профили эхолотирования, бурения, различных видов геофизического зондирования и др.). Морфометрия представляет собой научное направление, продолжающее на новом уровне морфологические исследования. Морфометрия развивается как отрасль знания, пограничная между геоморфологией, картографией, математикой и теорией измерений. Ее положение в системе наук схематично можно показать на рис. 1.

Рис.3.1 Положение морфометрии в системе наук

Для решения собственных задач специалисту-геоморфологу, ведущему морфометрические исследования, приходится собирать информацию не только о самом рельефе, но и о факторах и условиях его образования. Этим определяется предметная область или область интересов морфометрии. Эта область может расширяться или сужаться в зависимости от цели и задач конкретного исследования.

Базовой теоретической концепцией современной морфометрии является представление о том, что рельеф земной поверхности возникает вследствие перемещения вещества земной коры и что различные виды и способы этого перемещения должны отражаться и некоторое время сохраняться во внешнем облике рельефа. Свои суждения о происхождении и возрасте тех или иных форм рельефа морфометрия строит на принципах актуализма, сопоставляя ранее созданные формы рельефа с теми из них, которые формируются на глазах наблюдателя.

Значительной опорой для формирования суждений о происхождении рельефа являются результаты физического моделирования. Физическое моделирование дополняет визуальный анализ местности, создавая возможность для исследователя наблюдать изменение геометрических свойств рельефа в его динамике. В последние годы с развитием геоинформационных систем особую роль в морфометрических исследованиях приобрели автоматизированные методы морфометрического анализа цифровых моделей рельефа.

Внешний облик рельефа определяется закономерными сочетаниями характерных точек, линий, на которые как бы натянуты поверхности. Они то и образуют каркас рельефа (Ефремов, 1949; Спиридонов, 1970; и др.). Сочетания точек, линий и поверхностей создают в пространстве геометрические единства (или комплексы), определяющие внешний облик рельефа. Выделяя их в каждой форме рельефа, мы раскрываем морфологическое строение этих форм или их морфологическую структуру, а точки, линии и поверхности можно рассматривать в качестве ее элементов - элементов морфологической структуры. Анализ морфологической структуры и ее элементов составляет основу морфометрического анализа.

Нетрудно заметить, что каждый из элементов морфологической структуры выполняет определенные функции. Каждый из них не только позволяет увидеть различия внешнего облика форм рельефа, но определяет ход процессов современного рельефообразования. Отсюда можно говорить, что у каждого из элементов рельефа есть свои особые функции. Эти функции наиболее полно выявляются с помощью их геометрических характеристик. Точки и линии в рельефа обычно указывают на пространственное положение областей конвергенции (тальвеги, точки их слияния, центры воронок и впадин) и дивергенции (вершины, водораздельные линии и их аналоги) потоков вещества, участвующего в современном рельефообразовании.

Элементы морфологической структуры нетрудно объединить в геометрические классы: точки, линии, и поверхности. Каждый из классов можно изучать отдельно, выявляя их морфометрические особенности. В другом случае можно выяснять структуру сочетаний точек, линий и поверхностей. Последнее важно для анализа морфологических комплексов.

Морфометрические карты

В специальных работах, посвященных возможностям геоморфологического картографирования, можно увидеть большее разнообразие морфометрических карт. Число их растет по мере увеличения предложений по созданию морфометрических коэффициентов. К сожалению, систематического анализа этого морфометрического творчества никто не проводит. Один из наиболее полных систематических обзоров морфометрических карт был сделан достаточно давно А. И. Спиридоновым (1975). В этой работе он раздельно рассматривает существующие морфографические и морфометрические карты. Для морфометрических карт А. И. Спиридоновым предложен ряд классификаций. Основанием для их создания служит достаточно обоснованное мнение о том, что все разнообразие форм и количественных характеристик рельефа нельзя выразить каким-либо одним из существующих количественных показателей. По его мнению, лучше использовать 2-3 показателя. Среди них он в первую очередь называет характеристики густоты и глубины расчленения, а также крутизны земной поверхности.

Анализируя все многообразие уже имеющихся морфометрических карт, можно видеть, что они разделяются на две группы по способам изображения количественных характеристик рельефа. В первой из них количественная характеристика рельефа показывается с помощью изолиний. Предполагается, что в пространстве изображаемое свойство изменяется постепенно и непрерывно. Во второй группе карт те же характеристики относятся к определенной площади, которая подчеркивается проведением границ. На границах характеристика может не изменяться, подчеркивая тем самым сходство объектов, или изменяться скачкообразно, выявляя их различия. Изображение в этом случае подчеркивает дискретный характер происходящих в природе изменений. Дискретные морфометрические карты представляют собой картограммы.

Все морфометрические карты следует также разделять по способу получения количественных характеристик. Здесь также можно выделить два класса. Первый из них объединяет те карты, в которых количественная характеристик получена с помощью прямых измерений таких показателей, как абсолютная высота; относительные превышения объектов по отношению к базису денудации или какому-либо другому реперу; экспозиция и углы наклона поверхностей; длины линейных и иных объектов: их площади и объемы. Эти геометрические характеристики обычно важны для целей составления классификаций рельефа или для других морфогенетических, морфолитодина-мических или палеогеоморфологических целей.

Второй класс образуют карты, для составления которых требуются специальные расчеты некоторых коэффициентов. Они отражают не просто реальные геометрические параметры, а их соотношения. В последних наряду с геометрическими характеристиками форм содержится точка зрения их авторов на возможность использования этих отношений для описания качественных различий элементов и форм рельефа. Карты такого содержания чаще всего составляются в ходе решения прикладных геоморфологических задач. В настоящее время еще не выработаны правила их составления, а в некоторых из них просто нет ни геометрического, ни геоморфологического смысла.

3.2. Операции над морфометрическими картами и их преобразования

Большинство морфометрических карт представляют собой картографо-математические модели местности. Это позволяет проводить над ними некоторые операции, подобные арифметическим. В результате возникают как бы производные или преобразованные карты. Самыми простыми являются графические преобразования. С картами, как и с цифрами, можно проводить операции сложения, вычитания, деления, умножения, возведения в степень, извлечения корня и логарифмирования, можно дифференцировать и интегрировать, можно определять степень их корреляции. Действия над изолинейными и дискретными картами могут быть различными (Берлянт, 1978).

Примером графических преобразований карт является построение карт тектоморфоизогипс и карт изобазит, по В. П. Философову. В обоих случаях основанием служит топографическая карта. При построении карты тектоморфоизогипс спрямляют горизонтали, уничтожая формы рельефа эрозионного происхождения. Сначала убирают самые мелкие, затем все более крупные. Эта процедура проводится до тех пор, пока упрощенные в рисунке горизонтали (тектоморфоизогипсы) не будут рисовать горсты и грабены, своды и бассейны. Многоэтапное и последовательное упрощение рельефа позволяет специалисту выявить ту грань (тот рубеж) обобщения горизонталей, которая разделяет рисунок эрозионного расчленения от рисунка тектонического рельефа. Для построения карты изобазит необходимо уже две карты: топографическая и карта порядков эрозионных форм. Сначала на топографической карте выделяют только водотоки 1 порядка. Затем на основании анализа их гипсометрического положения, проводятся изолинии базисной поверхности. Эта поверхность как бы касается днищ эрозионных форм первого порядка снизу. Высота водораздельных пространств и тальвегов более высоких порядков при этом не учитывается. Затем выявляются долины 2 порядка, и строится базисная поверхность для водотоков второго порядка. Автор этой методики В. П. Философов считает, что с помощью карт изобазит последовательно выделяются тектонические структуры все более и более высокого порядка.

Сложение и вычитание карт и картограмм. Если на территорию имеется две морфометрические карты или картограммы одинакового масштаба и одинаковой проекции, то можно, если это имеет геоморфологический смысл, сложить их друг с другом или вычесть одну карту из другой. Для этого лучше всего сначала карту переделать в картограмму (перевести ее в растровый способ представления), показывающую те же свойства, но с помощью квадратной сетки. Чем мельче сетка, тем лучше результат. После получения картограмм обе карты можно представить в виде географических матриц. Сложение и вычитание карт производится поэлементно.

Не всякое сложение и вычитание карт-матриц целесообразно. Так, если из одной гипсометрической карты вычесть другую, например, из карты рельефа современной поверхности вычесть карту погребенного рельефа, то полученная карта будет картой мощности слоя. Такое действие имеет смысл. Сложение этих же карт явного смысла не имеет. Хотя последующее сравнение их с одной из карт-слагаемых может дать информацию о степени сходства погребенного и современного рельефа. Сложение карты подстилающего рельефа и карты мощности залегающей на нем толщи представляет собой действие, противоположное описанному выше вычитанию.

Произведение карт и картограмм. Морфометрическую карту (картограмму) можно умножить на некоторое постоянное число (скаляр), что даст преобразованную карту, на которой, по сравнению с исходной, увеличатся контрасты изображенных величин. Это кажется целесообразным тогда, когда необходимо подчеркнуть различия так, чтобы малые контрасты оставались малыми, а большие возросли тем больше, чем больше они на исходной карте. Можно умножать две гипсометрические карты друг на друга, если, хотя бы одна из них, характеризует погребенный рельеф, а другая - современный. Тогда, представив карты или картограммы в виде карт-матриц, их можно умножить поэлементно друг на друга.

Деление карт и картограмм. Морфометрическую карту и картограмму можно разделить на некоторое число (скаляр). Для этого следует представить карту в виде географической матрицы определенного порядка, и каждый ее элемент разделить на одно и то же число. Полученная карта-частное будет обладать меньшей контрастностью, что может в дальнейшем облегчить классификацию рельефа территории (в частности, объединение малых по размерам территорий в более крупные). При делении двух карт друг на друга, если на них показано одно и то же свойство (например, карту современного рельефа разделить на карту погребенного рельефа), образуется карта-отношение, на которой будет показано, во сколько раз современный рельеф в каждом своем элементе выше, чем погребенный. Это может оказаться полезным при совместном рассмотрении этой карты с картой-произведением. Здесь будут получены количественные значения величины инверсий и характер унаследованное™.

При делении друг на друга двух морфометрических карт различного содержания проводится поэлементное деление одной карты-матрицы на другую. Карта-частное имеет смысл пространственной характеристики удельной плотности величин. Она будет полезной в том случае, если частное двух величин будет иметь геоморфологический смысл. Например, если карта-частное будет иметь малую контрастность, то можно думать, что исходные карты обладают сходной пространственной структурой. При полном однообразии можно говорить о полной коррелированности карт. Во всех случаях полезно карту-частное сравнить с исходными картами. Сравнение позволит раскрыть разные отношения этих величин в пространстве. Здесь также могут быть хорошо видны и унаследованные (сопряженные) отношения, и инверсии.

Возведение в степень карт и картограмм. Поэлементное возведение в степень морфометрических карт и картограмм в определенном смысле аналогично произведению карты-матрицы на скаляр. Оно дает увеличение контрастности изображения, но степень контрастности окажется большей, чем при умножении карты-матрицы на скаляр.

Извлечение корня и логарифмирование карт и картограмм. Извлечение корня и логарифмирование морфометрических карт и картограмм, которые предварительно представлены в виде карт - географических матриц, если оно проводится поэлементно, направлены на сглаживание контрастов. Поэтому результат этих действий похож на результат процедуры деления, только он окажется иным, так как характер сглаживания будет более сильным.

Дифференцирование и интегрирование карт и картограмм. Эти процедуры возможны лишь для карт изолинейного типа. Для этой операции сначала необходимо получить конкретный вид функции анализируемого рельефа z=J(x,y). Это могут быть функции, описывающие современный рельеф или любые его морфометрические свойства (ведь и высота - это тоже одно из таких свойств) как функцию географических координат. Таким образом, в данном уравнении z -это любая морфометрическая характеристика; х и у - координаты. После дифференцирования будет получена другая функция z'=f(x,y). Если с ее помощью построить карту, то она будет уже характеризовать не z, а его градиент. Так, если продифференцировать функцию, описывающую поле высот, то мы получим поле уклонов.

Смысл интегрирования любой из морфометрических карт не всегда понятен. Но интегрирование карты углов наклона даст нам представления о распределении высот без их конкретной привязки к абсолютным их значениям. Содержательность интегрирования других морфометрических карт предстоит еще раскрыть.

Корреляционный анализ карт и картограмм. Если мы имеем две изолинейные карты, то, накладывая их друг на друга, можно получить много точек с характеристикой их пространственной корреляции. Легко можно принять, что две карты независимы, если их изолинии взаимно перпендикулярны друг другу. Если они параллельны, то между ними есть корреляция. Если они пересекаются под углом меньше 90°, то коэффициент их корреляции в точке пересечения изолиний равен косинусу угла пересечения.

Если на карте выделить достаточное число точек (лучше, если они будут набраны по регулярной сетке правильных треугольников), то можно построить карту изокоррелят. Степень коррелированности двух карт можно определить и иначе. Накладывая их друг на друга и измеряя в одних и тех же местах пары значений характеристик, мы получим два массива чисел. Корреляция между ними определяется аналитически.

В современных геоинформационных технологиях большинство морфометрических карт хранится в виде цифровых моделей. Для операций с ними разработаны специальные пакеты программ. Вышеперечисленные процедуры при использовании ЦМР можно проводить автоматически при помощи программных приложений: МАГ; Surfer; ArcGIS: 3D Analyst, Spatial Analyst, Geostatistical Analyst и др.

3.3. Основные алгоритмы составления производных морфометрических карт по ЦМР

После создания ЦМР и оценки ее качества можно приступать к описанию территории. Некоторые характеристики получаются непосредственно по имеющейся ЦМР. Это такие показатели, как высота поверхности в каждой точке, статистические показатели распределения высот, среднее значение высоты, максимальная и минимальная высоты в пределах участка. Анализ этих показателей может быть отображен на картах: высот рельефа (горизонталями, послойной окраской), гипсометрической и других.

Следующий этап - это построение производных ЦМР, к которым можно отнести модели углов наклона и экспозиции склонов, расстояния до водотоков (тальвегов) и т.п. По каждой из них или их комбинациям можно построить производные карты.

Создание производных цифровых моделей

Операции по исследованию цифровой модели для определения морфометрических характеристик рельефа, гидрологического анализа и решения многих других задач выполняют также на основе просмотра ЦМР скользящим окном. Порядок просмотра в алгоритмах задают одним из двух вариантов:

• рассматривают только четыре возможных направления (вверх, вниз, вправо, влево);

• рассматривают восемь возможных направлений (добавляются направления по диагоналям квадратной ячейки).

В обоих случаях направления просмотра нумеруют по часовой стрелке, как правило, начиная с направления вверх.

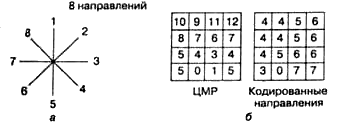
Рис.3.2 РИсследование ЦМР: а — кодирование направлений просмотра; б — кодирование направлений стока

Расчет углов наклона и экспозиций склонов

Использование ЦМР обеспечивает расчет разнообразных «частных характеристик» рельефа, под которыми понимаются производные от функции высот значения углов наклона, экспозиций и формы склонов. В первую очередь появились алгоритмы расчета углов наклона и экспозиций, которые параллельно и независимо разрабатывались в самых разнообразных целях, вошли в инструментарий практически всех программных средств ГИС, использовались для решения множества задач. Под углом наклона (крутизной ската, крутизной склона) понимается одна из характеристик пространственной ориентации элементарного склона — угол, образуемый направлением ската с горизонтальной плоскостью, выражаемый в градусах или в безразмерных величинах уклонов, равных тангенсам углов наклона, а также в процентах или промилле. Экспозиция склона численно равна азимуту проекции нормали склона на горизонтальную плоскость и выражается в градусах либо по 4, 8, 16 или 32 румбам (при этом экспозиция плоского склона с нулевой крутизной не определена).

Предложено множество формул и алгоритмов расчета углов наклона и экспозиций склонов, используемых при обработке растровых ЦМР в виде квадратной матрицы высот. Все они основаны на методе скользящего окна размером 2x2 или 3x3 точки с высотными отметками в узлах регулярной квадратной сети.

Оценка формы склонов

В продолжение анализа геометрических свойств окрестности точки на заданной криволинейной поверхности, соответствующей элементарному склону, можно оценить его форму. Методы такой оценки предлагались неоднократно. К примеру, в работе, посвященной автоматизации построения карт ориентации, формы и относительной освещенности склонов, предлагался алгоритм классификации элементарных склонов по типам их поперечного и продольного профилей в соответствии с подходом к типологии элементарных форм Ю. К. Ефремова [А. В. Кошкарев, 1980]. При этом под профилем склона понималась величина (или знак) радиуса кривизны нормального сечения склона в направлении линии наибольшего ската (поперечный профиль) или в перпендикулярном ему направлении (продольный профиль). С точки зрения формализмов дифференциальной геометрии им будут соответствовать частные производные второго порядка от функции рельефа (градиенты изогради-ентной поверхности). Пример расчета формы склонов в среде ГИС, основанного на сходной типологии элементарных форм (рис. 3), приводит Р.Дикау  в рамках предложенной им «цифровой геоморфологической модели рельефа», включающей не только собственно ЦМР, но и процедуры ее обработки и расчетные результаты в форме набора 30 морфометрических характеристик рельефа.

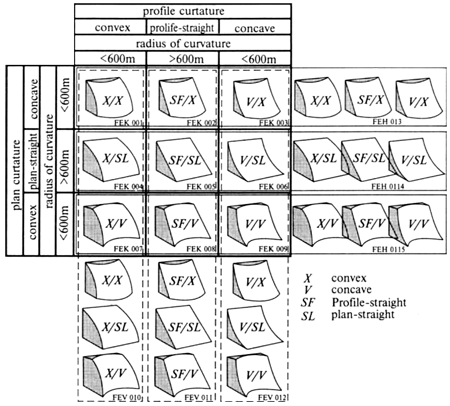
Рис.3.3 Классификация элементарных форм склонов по соотношению радиусов кривизны (radius of curvature) их продольного и поперечного сечений (plan curvature и profile curvature) с подразделением на выпуклые (convex), плоские (plan) и вогнутые (concave) (рисунок из учебника «Геоинформатика» под ред. В.С. Тикунова, 2005):
X — выпуклые; V — вогнутые; SF — плоские в плане; SL — плоские в поперечном сечении. Порог плоскости — значение радиуса кривизны более 600 м. Помимо 9 сочетаний (выпукло-вогнутые, плосковыпуклые и т. п.), выраженных элементарными классами FEK 001 —FEK 009, рассматриваются обобщенные классы форм, индексированные как FEV 010—FEV 012 и FEH 013 —FEH 015 в профиле и плане соответственно

Очевидным продолжением этой линии «элементаризации земной поверхности» следует считать систематику А. Н. Ласточкина, включающую характерные точки и структурные линии рельефа (в том числе линии перегиба продольного и поперечного профилей), а также элементарные поверхности — морфологические элементы, ограниченные морфоизографами (линиями с нулевыми значениями горизонтальной кривизны, отделяющими выпуклые, вогнутые и прямолинейные в плане элементы) и классифицируемые по типам профиля склона и другим морфографическим признакам.

Генерация сети тальвегов и водоразделов

Расчет структурных элементов рельефа, образующих его каркас, т.е. экстракция из ЦМР линейных элементов, обычно называемых линиями тальвегов и линиями водоразделов, а в более общем виде, имея в виду рельеф не только суши, но и дна океанов и внутренних водоемов, — килевыми и гребневыми, или базисными и вершинными, предполагает моделирование линий поверхностного стока. Для матричной ЦМР направление стока из каждой ее ячейки будет определяться соотношением ее высотной отметки с высотными отметками 4 или 8 соседних ячеек. Таким образом могут быть найдены все ячейки, образующие водосбор, и оконтурена его граница (линия водораздела), а линии стока будут определять эрозионную сеть, примерно соответствующую тальвегам. Рис. 4 иллюстрирует результаты выделения элементарных водосборов для целей их классификации.

Более «изощренные» и эффективные способы выделения линий тальвегов и водоразделов основаны на формализмах дифференциальной геометрии (подобных тем, какие используются в ранее упомянутых алгоритмах расчета кривизны склонов для оценки их формы), позволяя экстрагировать из ЦМР не только тальвеги и водоразделы, но иные структурные линии, включая бровки, швы, ребра и гребни, небезынтересные с точки зрения морфометрических приложений функций обработки ЦМР.

Рис.3.4 Классификация элементарных водосборов по их площади (catchment area sizes), полученная путем каскадной обработки ЦМР в виде модели TIN; стрелки соответствуют линиям наибольшего ската и указывают направление стока

Аналитическая отмывка рельефа. Автоматизация светотеневой отмывки рельефа — наиболее пластического и широко рас пространенного способа картографического изображения рельефа на средне- и мелкомасштабных топографических и общегеографических картах в сочетании с гипсометрической его характеристикой или изображением в горизонталях (изобатах) — одна из прикладных задач, поставленных и решенных уже в первых экспериментах по обработке ЦМР в 60-х годах, в условиях использования современных программных средств ГИС стала рутинной процедурой. Ее реализация основана на расчете относительных освещенностей склонов, точнее участков склонов, «элементарных склонов», образованных треугольными гранями модели TIN или плоскостями ячеек матрицы высот. Освещенность вычисляется по формуле

I = cosφ,

где I — относительная освещенность; φ — угол между вектором направления на источник освещения и вектором нормали к плоскости элементарного склона [Ю.Л.Костюк, 2000], или по другой формуле, удобной для вычислений при уже известных значениях угла наклона и экспозиции и пригодной для расчета реального солнечного освещения (инсоляции):

I = sin β,

где β — угол падения луча на плоскость элементарного склона; или

I = sin{arctg[tgαcos(A_ε –   A₀)] + β₀},

где α — угол наклона элементарного склона; A_ε — экспозиция склона, измеряемая истинным (астрономическим) азимутом; β₀ — высота источника света (Солнца) над горизонтом; A₀ — истинный азимут источника света. Освещенность принимается равной нулю, если источник освещения находится под плоскостью элементарного склона (φ≥90° или β≤0°). Обычно источник помещают на северо-западе, как это принято при ручном исполнении отмывки рельефа.

Трехмерное представление рельефа

Трехмерное представление рельефа в виде светотеневого или нитяного (каркасного) изображения (блок-диаграммы) — еще одна из широко распространенных функций обработки ЦМР (рис. 5).

Рис.3.5 Трехмерное светотеневое изображение рельефа участка строительства Рогунской ГЭС (Таджикистан)

В основе построения таких изображений (по крайней мере, основанных на представлении ЦМР моделью TIN) лежат алгоритмы компьютерной графики, разрешающие проблему удаления невидимых поверхностей при формировании трехмерных сцен и их проецировании на плоскость.

В сочетании с «драпировкой» цифровым изображением местности такое трехмерное (точнее, 2,5-мерное) изображение рельефа способно дать ее высокореалистичный вид с высоты «птичьего полета». Динамическая серия таких изображений, имитирующая полет летательного аппарата, принадлежащая к классу виртуально-реальностных изображений, широко используется в оборонных приложениях при обучении авиаэкипажей.