Билет № 16 Практическое задание Решение задачи по теме «Системы счисления» с использованием стандартной программы «Калькулятор». Перевод чисел из десятичной системы счисления в двоичную, и обратно. Проверка с помощью «Калькулятора».

Билет № 16

Практическое задание Решение задачи по теме «Системы счисления» с использованием стандартной программы «Калькулятор». Перевод чисел из десятичной  системы счисления в двоичную, и обратно. Проверка с помощью «Калькулятора».

В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от позиции. Количество используемых цифр называется основанием позиционной системы счисления.

К позиционным системам счисления относятся двоичная, десятичная, восьмеричная, шестнадцатеричная.

Здесь любое число записывается последовательностью цифр соответствующего алфавита, причем значение каждой цифры зависит от места (позиции), которое она занимает в этой последовательности. Например, в записи 555, сделанной в десятичной системе счисления, использована одна цифра 5, но в зависимости от занимаемого ею места она имеет разное количественное значение – 5 единиц, 5 десятков или 5 сотен. Поэтому справедливы равенства (подстрочные индексы применим для указания, в какой системе счисления записано число):

555,5₁₀=5*10²+5* 10¹+5* 10⁰+5* 10^-1;

В современных компьютерах применяются позиционные системы счисления, в основном двоичная система.

Перевод числа из десятичной системы счисления в двоичную Пусть требуется найти представление числа 12₁₀ в двоичной системе счисления

Поступаем следующим образом: делим, начиная с 12, каждое получающееся частное на основание системы, в которую переводим число, то есть на 2. Получаем:

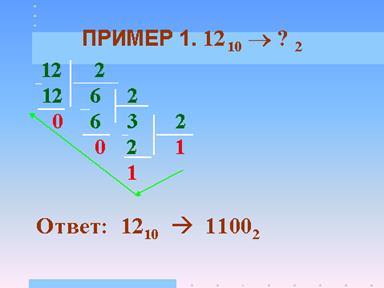Затем в направлении, указанном стрелкой, начиная с последнего частного (в нашем случае оно всегда будет равно 1), записываемого в старший разряд формируемого двоичного представления, фиксируем все остатки. В итоге получаем ответ: 12₁₀= 1100₂.

Перевод числа из двоичной системы счисления в десятичную. Это перевод – как бы обратный к изложенному выше. Его наиболее просто осуществить, основываясь на позиционности двоичной системы счисления. Уже отмечалась правомерность записи двоичного числа в виде суммы степеней основания системы счисления, то есть степеней двойки. Сделав такую запись, надо подсчитать десятичное значение полученной суммы:

101₂=(1· 2² +0· 2¹ + 1· 2⁰)₁₀=(4+1)₁₀=5₁₀

1101₂=(1· 2³ + 1· 2² + 0· 2¹ + 1· 2⁰)₁₀ = (8+4)₁₀=12₁₀

Действительно, известно, что

2⁰ = 1, 2¹ = 2, 2² = 4, 2³ = 8, 2⁴ = 16, 2⁵ = 32, 2⁶ = 64, 2⁷=128,

2⁸ = 256, 2⁹=512, 2¹⁰ = 1024.

Задание:

1. Переведите в двоичную систему десятичные числа:

·   45

·   99

·   123

2. Переведите в двоичную систему десятичные числа:

·         111₂

·         10110₂

·         1010101₂

Проверить с помощью «Калькулятора».