Быстрый способ решения задач по физике

Быстрый способ решения задач по физике или как решить задачу с помощью метода размерностей.

Самой главной задачей учителя, на мой взгляд, является умение заинтересовать учащегося, вызвать у него желание заниматься данным предметом. Физика – это один из таких предметов, которого бояться многие школьники, поскольку считают его очень сложным и непонятным. Поэтому мне хотелось бы предложить один из необычных способов решения школьных задач, который очень заинтересовал учеников моего класса, и , надеюсь, заинтересует и остальных школьников и учителей. К тому же стоит подчеркнуть, что  решение задач, с помощью метода размерностей, позволяет развивать логическое мышление у учеников , учит их рассуждать и делать осознанные умозаключения.

Очень часто нам приходится сталкиваться с задачами, которые на первый взгляд просто невозможно решить. Но стоит только воспользоваться методом размерностей, как задача моментально решается! Данный метод позволяется получать формулы, описывающие сложные физические закономерности, исходя из простых логических соображений. Для того чтобы воспользоваться методом размерности совсем не обязательно быть ассом в физике, достаточно знать основные законы природы и..получается готовая формула для решения задачи.  Итак, перейдём от слов к практике –сформулируем основные правила, пользуясь которыми можно решить задачу с помощью данного метода. Но самое главное, дадим определение понятию «размерность».

Выражение единиц измерения произвольной  физической величины через единицы измерения основных величин называется размерностью.

1.     Размерность произвольной физической величины может быть только произведением степеней размерностей величин, принятых за основные.

2.     Размерности обеих частей равенства, отражающие некоторую физическую закономерность, должны быть одинаковыми.

Конечно, на первый взгляд эти правила кажутся непонятными, но мы разберём их применение на практике и рассмотрим, как можно решить задачу, применяя данный метод.

Задача 1.

Найти выражение для периода колебаний математического маятника.

Решение

Первым делом нам необходимо определить от чего будет зависеть период колебаний T. Сделаем предположение, что он будет зависеть от длины подвеса l, массы груза m и ускорения свободного падения g.

Примем за основные три  единицы измерения: единицу массы M килограммы, единицу длины L метры и единицу времени T секунды.

А теперь выразим единицы измерения всех, используемых нами, величин с помощью основных единиц.

[T]=с=T               [l]=м=L                [m]=кг=M            [g]=м*с^-2=L*T^-2

Мы ищем зависимость вида

Составим таблицу, которая будет отражать степени, в которые возводятся основные величины.

Обозначим степени l за α, m-за β, а g-за γ. А теперь, пользуясь нашими правилами, составим безразмерную комбинацию, которая позволит определить нам вид функции, для нахождения периода колебаний.

А теперь, пользуясь свойствами показателя степени, получим систему уравнений.

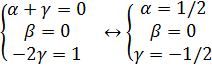
А теперь, зная все степени, можем получить выражение для периода колебаний математического маятника.

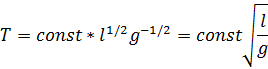
Как видно из решения, мы сделали не совсем верное предположение, когда включили массу груза в выражение для периода, но данное допущение не принесло нам никаких неприятностей. На мой взгляд, в этом и заключается прелесть данного метода - он позволяет самостоятельно размышлять и делать предположения.

Выражение для периода мы получили с точностью до константы, которую можно определить из эксперимента, как известно, она равна 2π.

Мне хотелось бы рассмотреть ещё одну задачу, на примере которой можно продемонстрировать «силу» метода размерности.

Задача 2

В атмосфере произошёл сильный точечный взрыв. Найти выражение для нахождения радиуса поражения.

Решение

Будем предполагать, что радиус зависит от следующих величин: плотность воздуха ρ, энергия взрыва E и продолжительность взрыва t.

Найдём размерности каждой величины:

[r]=L           [E]=L²*M*T^-2                [t]=T           [ρ]=M*L^-3

Обозначим показатель степени Е через α, t – через β, а ρ – через γ

Получим систему уравнений

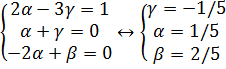
Итого, подставляя полученные степени, получаем исходную формулу:

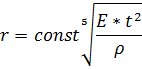
Итак, с помощью простых соображений мы получили формулу, с помощью которой можно рассчитать радиус поражения при сильном взрыве в атмосфере.

В заключение мне хочется сказать, что данный метод мне кажется очень полезным для школьников, поскольку учит их размышлять, выходя за рамки материала урока. Надеюсь, данная статья будет полезна и для других учителей.

Агарёва Анастасия Александровна учитель физики «Лицей №4»

Список литературы

1.      В.А. Фабрикант « О современной физике – учителю» М., «Знание», 1975

2.      Р. Курт « Анализ размерностей в астрофизике» М., «Мир», 1975

3.      Д.И. Трубецков « Колебания. Волны. Электроны». Государственный учебно-научный центр» Колледж», 1993.

4.