Диагностическая работа по математике 11 класс Профильный уровень

Диагностическая работа№2        Профильный уровень                           15.12.2016

ВАРИАНТ№1

1. Уста­нов­ка двух счётчи­ков воды (хо­лод­ной и го­ря­чей) стоит 2500 руб­лей. До уста­нов­ки счётчи­ков за воду пла­ти­ли 800 руб­лей еже­ме­сяч­но. После уста­нов­ки счётчи­ков еже­ме­сяч­ная опла­та воды стала со­став­лять 600 руб­лей. Через какое наи­мень­шее ко­ли­че­ство ме­ся­цев эко­но­мия по опла­те воды пре­вы­сит за­тра­ты на уста­нов­ку счётчи­ков, если та­ри­фы на воду не из­ме­нят­ся?

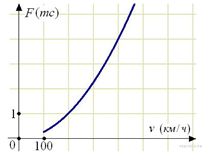
2.  Когда са­мо­лет на­хо­дит­ся в го­ри­зон­таль­ном по­ле­те, подъ­ем­ная сила, дей­ству­ю­щая на кры­лья, за­ви­сит толь­ко от ско­ро­сти. На ри­сун­ке изоб­ра­же­на эта за­ви­си­мость для не­ко­то­ро­го са­мо­ле­та. На оси абс­цисс от­кла­ды­ва­ет­ся ско­рость (в ки­ло­мет­рах в час), на оси ор­ди­нат – сила (в тон­нах силы). Опре­де­ли­те по ри­сун­ку, при какой ско­ро­сти (в ки­ло­мет­рах в час) подъ­ем­ная сила до­сти­га­ет 1 тонн силы?

                        

 

3. На клет­ча­той бу­ма­ге изоб­ра­же­ны два круга. Пло­щадь внут­рен­не­го круга равна 4. Най­ди­те пло­щадь за­штри­хо­ван­ной фи­гу­ры.

  4. На чем­пи­о­на­те по прыж­кам в воду вы­сту­па­ют 50 спортс­ме­нов, среди них 8 пры­гу­нов из Рос­сии и 10 пры­гу­нов из Мек­си­ки. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Най­ди­те ве­ро­ят­ность того, что пят­на­дца­тым будет вы­сту­пать пры­гун из Рос­сии.

5. Най­ди­те корни урав­не­ния:      В ответ за­пи­ши­те наи­боль­ший от­ри­ца­тель­ный ко­рень.

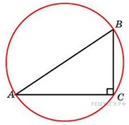
6. Ра­ди­ус окруж­но­сти, опи­сан­ной около пря­мо­уголь­но­го тре­уголь­ни­ка, равен 4. Най­ди­те ги­по­те­ну­зу этого тре­уголь­ни­ка.

                            

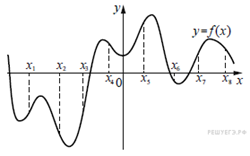
7. На ри­сун­ке изоб­ражён гра­фик функ­ции y = f(x). На оси абс­цисс от­ме­че­ны во­семь точек: x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈. В сколь­ких из этих точек про­из­вод­ная функ­ции f(x) от­ри­ца­тель­на?

 

8. Объем куба равен    . Най­ди­те его диа­го­наль.

 

 

9. Най­ди­те зна­че­ние вы­ра­же­ния              .

10. Ко­эф­фи­ци­ент по­лез­но­го дей­ствия (КПД) не­ко­то­ро­го дви­га­те­ля опре­де­ля­ет­ся фор­му­лой , где – тем­пе­ра­ту­ра на­гре­ва­те­ля (в гра­ду­сах Кель­ви­на), – тем­пе­ра­ту­ра хо­ло­диль­ни­ка (в гра­ду­сах Кель­ви­на). При какой ми­ни­маль­ной тем­пе­ра­ту­ре на­гре­ва­те­ля КПД этого дви­га­те­ля будет не мень­ше , если тем­пе­ра­ту­ра хо­ло­диль­ни­ка К? Ответ вы­ра­зи­те в гра­ду­сах Кель­ви­на.

11. То­вар­ный поезд каж­дую ми­ну­ту про­ез­жа­ет на 300 мет­ров мень­ше, чем ско­рый, и на путь в 420 км тра­тит вре­ме­ни на 3 часа боль­ше, чем ско­рый. Най­ди­те ско­рость то­вар­но­го по­ез­да. Ответ дайте в км/ч.

12. Най­ди­те точку мак­си­му­ма функ­ции     ,   при­над­ле­жа­щую про­ме­жут­ку .

13. а) Ре­ши­те урав­не­ние      

б) Ука­жи­те корни урав­не­ния, при­над­ле­жа­щие от­рез­ку

14. В пра­виль­ной тре­уголь­ной приз­ме ABCA₁B₁C₁, все рёбра ко­то­рой равны 1, най­ди­те рас­сто­я­ние между пря­мы­ми AA₁ и BC₁.

15. Ре­ши­те не­ра­вен­ство:

16. Внев­пи­сан­ной окруж­но­стью тре­уголь­ни­ка на­зы­ва­ет­ся окруж­ность, ка­са­ю­ща­я­ся одной сто­ро­ны тре­уголь­ни­ка и про­дол­же­ний двух дру­гих его сто­рон. Ра­ди­у­сы двух внев­пи­сан­ных окруж­но­стей пря­мо­уголь­но­го тре­уголь­ни­ка равны 1 и 7. Най­ди­те рас­сто­я­ние между их цен­тра­ми.

17. Из­вест­но, что вклад, на­хо­дя­щий­ся в банке с на­ча­ла года, воз­рас­та­ет к концу года на опре­де­лен­ный про­цент, свой для каж­до­го банка. В на­ча­ле года Сте­пан по­ло­жил 60% не­ко­то­рой суммы денег в пер­вый банк, а остав­шу­ю­ся часть суммы во вто­рой банк. К концу года сумма этих вкла­дов стала равна 590 000 руб., а к концу сле­ду­ю­ще­го года 701 000 руб. Если бы Сте­пан пер­во­на­чаль­но по­ло­жил 60% своей суммы во вто­рой банк, а остав­шу­ю­ся часть в пер­вый, то по ис­те­че­нии од­но­го года сумма вкла­дов стала бы рав­ной 610 000 руб. Ка­ко­ва была бы сумма вкла­дов в этом слу­чае к концу вто­ро­го года?

18. Най­ди­те все зна­че­ния а, при каж­дом из ко­то­рых ре­ше­ния не­ра­вен­ства об­ра­зу­ют от­ре­зок длины 1.

19. На доске на­пи­са­ли не­сколь­ко не обя­за­тель­но раз­лич­ных дву­знач­ных на­ту­раль­ных чисел без нулей в де­ся­тич­ной за­пи­си. Сумма этих чисел ока­за­лась рав­ной 2970. В каж­дом числе по­ме­ня­ли ме­ста­ми первую и вто­рую цифры (на­при­мер, число 16 за­ме­ни­ли на число 61).

а) При­ве­ди­те при­мер ис­ход­ных чисел, для ко­то­рых сумма по­лу­чив­ших­ся чисел ровно в 3 раза мень­ше, чем сумма ис­ход­ных чисел.

б) Могла ли сумма по­лу­чив­ших­ся чисел быть ровно в 5 раз мень­ше, чем сумма ис­ход­ных чисел?

в) Най­ди­те наи­мень­шее воз­можн­ное зна­че­ние суммы по­лу­чив­шиъ­ся чисел.

 

Диагностическая работа№2                                   15.12.2016

ВАРИАНТ№2

 

1. В доме, в ко­то­ром живет Вася, один подъ­езд. На каж­дом этаже на­хо­дит­ся по 4 квар­ти­ры. Вася живет в квар­ти­ре №71. На каком этаже живет Вася?

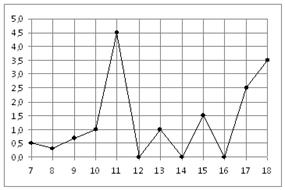
2. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­но су­точ­ное ко­ли­че­ство осад­ков, вы­па­дав­ших в Эли­сте с 7 по 18 де­каб­ря 2001 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство осад­ков, вы­пав­ших в со­от­вет­ству­ю­щий день, в мил­ли­мет­рах. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, сколь­ко дней за дан­ный пе­ри­од не вы­па­да­ло осад­ков.

            

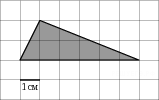
3. Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

4. Кон­курс ис­пол­ни­те­лей про­во­дит­ся в 3 дня. Всего за­яв­ле­но 40 вы­ступ­ле­ний — по од­но­му от каж­дой стра­ны. Ис­пол­ни­тель из Рос­сии участ­ву­ет в кон­кур­се. В пер­вый день 18 вы­ступ­ле­ний, осталь­ные рас­пре­де­ле­ны по­ров­ну между остав­ши­ми­ся днями. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что вы­ступ­ле­ние пред­ста­ви­те­ля Рос­сии со­сто­ит­ся в тре­тий день кон­кур­са?

5. Най­ди­те ко­рень урав­не­ния               .

6. Най­ди­те пе­ри­метр пря­мо­уголь­ни­ка, если его пло­щадь равна 176, а от­но­ше­ние со­сед­них сто­рон 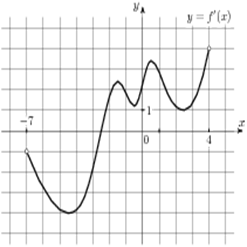равно 4 : 11.

7. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции , опре­де­лен­ной на ин­тер­ва­ле (−7; 4). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции . В от­ве­те ука­жи­те сумму целых точек, вхо­дя­щих в эти про­ме­жут­ки.

8. Конус впи­сан в шар. Ра­ди­ус ос­но­ва­ния ко­ну­са равен ра­ди­у­су шара. Объем ко­ну­са равен 6. Най­ди­те объем шара.

 

9. Най­ди­те зна­че­ние вы­ра­же­ния .

10. Сила тока в цепи (в ам­пе­рах) опре­де­ля­ет­ся на­пря­же­ни­ем в цепи и со­про­тив­ле­ни­ем элек­тро­при­бо­ра по за­ко­ну Ома: , где  — на­пря­же­ние в воль­тах,  — со­про­тив­ле­ние элек­тро­при­бо­ра в омах. В элек­тро­сеть включeн предо­хра­ни­тель, ко­то­рый пла­вит­ся, если сила тока пре­вы­ша­ет 2,5 А. Опре­де­ли­те, какое ми­ни­маль­ное со­про­тив­ле­ние долж­но быть у элек­тро­при­бо­ра, под­клю­ча­е­мо­го к ро­зет­ке в 220 вольт, чтобы сеть про­дол­жа­ла ра­бо­тать. Ответ вы­ра­зи­те в омах.

11. Пер­вая труба про­пус­ка­ет на 4 литра воды в ми­ну­ту мень­ше, чем вто­рая. Сколь­ко лит­ров воды в ми­ну­ту про­пус­ка­ет вто­рая труба, если ре­зер­ву­ар объ­е­мом 96 лит­ров она за­пол­ня­ет на 4 ми­ну­ты быст­рее, чем пер­вая труба?

12. Най­ди­те точку мак­си­му­ма функ­ции .

13. а) Ре­ши­те урав­не­ние          

б) Ука­жи­те корни этого урав­не­ния, при­над­ле­жа­ще­го от­рез­ку

14. В пра­виль­ной че­ты­рех­уголь­ной приз­ме KLMNK₁L₁M₁N₁ точка E делит бо­ко­вое ребро KK₁ в от­но­ше­нии KE : EK₁ = 1 : 3. Через точки L и E про­ве­де­на плос­кость па­рал­лель­ная пря­мой KM и пе­ре­се­ка­ю­щая ребро NN₁ в точке F.

а) До­ка­жи­те, что плос­кость делит ребро NN₁ по­по­лам.

б) Най­ди­те угол между плос­ко­стью и плос­ко­стью грани KLMN, если из­вест­но, что KL = 6 , KK₁ = 4 .

15. Ре­ши­те не­ра­вен­ство: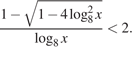

16. Точка M лежит на от­рез­ке AB. На окруж­но­сти с диа­мет­ром AB взята точка C, уда­лен­ная от точек A, M и B на рас­сто­я­ния 20, 14 и 15 со­от­вет­ствен­но. Най­ди­те пло­щадь тре­уголь­ни­ка BMC.

17. В банк был по­ло­жен вклад под бан­ков­ский про­цент 10%. Через год хо­зя­ин вкла­да снял со счета 2000 руб­лей, а еще через год снова внес 2000 руб­лей. Од­на­ко, вслед­ствие этих дей­ствий через три года со вре­ме­ни пер­во­на­чаль­но­го вло­же­ния вкла­да он по­лу­чил сумму мень­ше за­пла­ни­ро­ван­ной (если бы не было про­ме­жу­точ­ных опе­ра­ций со вкла­дом). На сколь­ко руб­лей мень­ше за­пла­ни­ро­ван­ной суммы по­лу­чил в итоге вклад­чик?

18. Най­ди­те все по­ло­жи­тель­ные зна­че­ния а, при каж­дом из ко­то­рых си­сте­ма 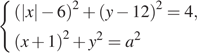     имеет един­ствен­ное ре­ше­ние.

19. В игре «Дро­ти­ки» есть 20 на­руж­ных сек­то­ров, про­ну­ме­ро­ван­ных от 1 до 20 и два цен­траль­ных сек­то­ра. При по­па­да­нии в на­руж­ный сек­тор игрок по­лу­ча­ет ко­ли­че­ство очков, сов­па­да­ю­щее с но­ме­ром сек­то­ра, а за по­па­да­ние в цен­траль­ные сек­то­ра он по­лу­ча­ет 25 или 50 очков со­от­вет­ствен­но. В каж­дом из на­руж­ных сек­то­ров есть об­ла­сти удво­е­ния и утро­е­ния, ко­то­рые, со­от­вет­ствен­но, удва­и­ва­ют или утра­и­ва­ют но­ми­нал сек­то­ра. Так, на­при­мер, по­па­да­ние в сек­тор 10 (не в зоны удво­е­ния и утро­е­ния) дает 10 очков, в зону удво­е­ния сек­то­ра ― 20 очков, в зону утро­е­ния ― 30 очков.

а) Может ли игрок тремя брос­ка­ми на­брать ровно 167 очков?

б) Может ли игрок ше­стью брос­ка­ми на­брать ровно 356 очков?

в) С по­мо­щью ка­ко­го наи­мень­ше­го ко­ли­че­ства брос­ков, игрок может на­брать ровно 1001 очко?

 

Диагностическая работа№2     Профильный уровень                               15.12.2016

ВАРИАНТ№3

1. Бегун про­бе­жал 180 мет­ров за 20 се­кунд. Най­ди­те сред­нюю ско­рость бе­гу­на. Ответ дайте в ки­ло­мет­рах в час.

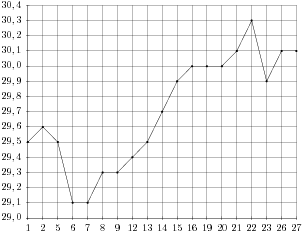
2. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­зан курс ав­стра­лий­ско­го дол­ла­ра, уста­нов­лен­ный Цен­тро­бан­ком РФ, во все ра­бо­чие дни с 1 по 27 ок­тяб­ря 2010 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — цена дол­ла­ра в руб­лях. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, какой был курс дол­ла­ра 12 ок­тяб­ря. Ответ дайте в руб­лях.

 

              

 

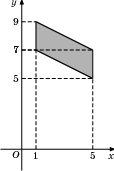
3. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, вер­ши­ны ко­то­ро­го имеют ко­ор­ди­на­ты (1;7), (5;5), (5;7), (1;9).

4. На кла­ви­а­ту­ре те­ле­фо­на 10 цифр, от 0 до 9. Ка­ко­ва ве­ро­ят­ность того, что слу­чай­но на­жа­тая цифра будет боль­ше 2, но мень­ше 7?

 5. Ре­ши­те урав­не­ние .

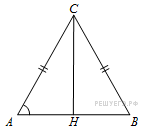
6. В тре­уголь­ни­ке ABC AC = BC = 5,             Най­ди­те АВ.

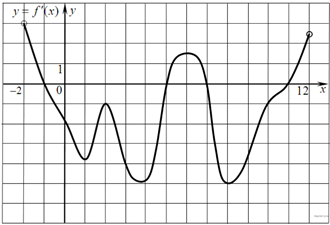
7. На ри­сун­ке изоб­ра­жен гра­фик про­из­вод­ной функ­ции f(x), опре­де­лен­ной на ин­тер­ва­ле (−2; 12). Най­ди­те про­ме­жут­ки убы­ва­ния функ­ции f(x). В от­ве­те ука­жи­те длину наи­боль­ше­го из них.

                          

8. Пло­щадь бо­ко­вой по­верх­но­сти ци­лин­дра равна , а вы­со­та — 4. Най­ди­те диа­метр ос­но­ва­ния.

9. Най­ди­те зна­че­ние вы­ра­же­ния                 .

10. Мяч бро­си­ли под углом к плос­кой го­ри­зон­таль­ной по­верх­но­сти земли. Время полeта мяча (в се­кун­дах) опре­де­ля­ет­ся по фор­му­ле     . При каком зна­че­нии угла (в гра­ду­сах) время полeта со­ста­вит 3 се­кун­ды, если мяч бро­са­ют с на­чаль­ной ско­ро­стью м/с? Счи­тай­те, что уско­ре­ние сво­бод­но­го па­де­ния м/с.

11. Игорь и Паша кра­сят забор за 9 часов. Паша и Во­ло­дя кра­сят этот же забор за 12 часов, а Во­ло­дя и Игорь – за 18 часов. За сколь­ко часов маль­чи­ки по­кра­сят забор, ра­бо­тая втро­ем?

12. Най­ди­те точку ми­ни­му­ма функ­ции .

13. а) Ре­ши­те урав­не­ние        

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку      

14. Все рёбра пра­виль­ной тре­уголь­ной пи­ра­ми­ды SBCD с вер­ши­ной S равны 9.

Ос­но­ва­ние O вы­со­ты SO этой пи­ра­ми­ды яв­ля­ет­ся се­ре­ди­ной от­рез­ка SS₁, M — се­ре­ди­на ребра SB , точка L лежит на ребре CD так, что CL : LD = 7 : 2.

а) До­ка­жи­те, что се­че­ние пи­ра­ми­ды SBCD плос­ко­стью S₁LM — рав­но­бо­кая тра­пе­ция.

б) Вы­чис­ли­те длину сред­ней линии этой тра­пе­ции.

15. Ре­ши­те не­ра­вен­ство:

16. В тре­уголь­ни­ке из­вест­ны сто­ро­ны: Окруж­ность, про­хо­дя­щая через точки и пе­ре­се­ка­ет пря­мые и со­от­вет­ствен­но в точ­ках и от­лич­ных от вер­шин тре­уголь­ни­ка. От­ре­зок ка­са­ет­ся окруж­но­сти, впи­сан­ной в тре­уголь­ник Най­ди­те длину от­рез­ка

17. В банк был по­ло­жен вклад под бан­ков­ский про­цент 10%. Через год хо­зя­ин вкла­да снял со счета 2000 руб­лей, а еще через год снова внес 2000 руб­лей. Од­на­ко, вслед­ствие этих дей­ствий через три года со вре­ме­ни пер­во­на­чаль­но­го вло­же­ния вкла­да он по­лу­чил сумму мень­ше за­пла­ни­ро­ван­ной (если бы не было про­ме­жу­точ­ных опе­ра­ций со вкла­дом). На сколь­ко руб­лей мень­ше за­пла­ни­ро­ван­ной суммы по­лу­чил в итоге вклад­чик?

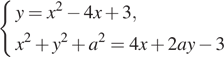18. При каких зна­че­ни­ях па­ра­мет­ра си­сте­ма имеет ре­ше­ния?

19. По­след­ние члены двух ко­неч­ных ариф­ме­ти­че­ских про­грес­сий a₁ = 5, a₂ = 8, ..., a_N и b₁ = 9, b₂ = 14, ..., b_M сов­па­да­ют, а сумма всех сов­па­да­ю­щих (взя­тых по од­но­му разу) чле­нов этих про­грес­сий равна 815. Най­ди­те число чле­нов в каж­дой про­грес­сии.

 

 

 

Диагностическая работа№2     Профильный уровень                               15.12.2016

ВАРИАНТ№4

1. Поезд Москва-Орен­бург от­прав­ля­ет­ся в 17:25, а при­бы­ва­ет в 19:25 на сле­ду­ю­щий день (время мос­ков­ское). Сколь­ко часов поезд на­хо­дит­ся в пути?

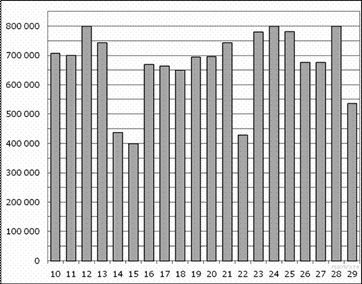
2. На диа­грам­ме по­ка­за­но ко­ли­че­ство по­се­ти­те­лей сайта РИА Но­во­сти во все дни с 10 по 29 но­яб­ря 2009 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся дни ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство по­се­ти­те­лей сайта за дан­ный день. Опре­де­ли­те по диа­грам­ме, во сколь­ко раз наи­боль­шее ко­ли­че­ство по­се­ти­те­лей боль­ше, чем наи­мень­шее ко­ли­че­ство по­се­ти­те­лей за день.

             

3. Най­ди­те пло­щадь па­рал­ле­ло­грам­ма, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

4. Кон­курс ис­пол­ни­те­лей про­во­дит­ся в 4 дня. Всего за­яв­ле­но 50 вы­ступ­ле­ний — по од­но­му от каж­дой стра­ны, участ­ву­ю­щей в кон­кур­се. Ис­пол­ни­тель из Рос­сии участ­ву­ет в кон­кур­се. В пер­вый день 20 вы­ступ­ле­ний, осталь­ные рас­пре­де­ле­ны по­ров­ну между остав­ши­ми­ся днями. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что вы­ступ­ле­ние пред­ста­ви­те­ля Рос­сии со­сто­ит­ся в тре­тий день кон­кур­са?

5. Ре­ши­те урав­не­ние      .   = - от­ве­те на­пи­ши­те наи­мень­ший по­ло­жи­тель­ный ко­рень. 6.В тре­уголь­ни­ке ABC угол C равен 90°, АС = 4.   Най­ди­те АВ. 

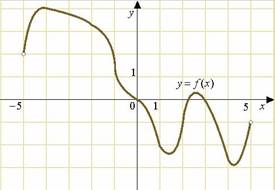
7. На ри­сун­ке изоб­ра­жен гра­фик функ­ции  y = f(x), опре­де­лен­ной на ин­тер­ва­ле (-5;5). Опре­де­ли­те ко­ли­че­ство целых точек, в ко­то­рых про­из­вод­ная функ­ции  y = f(x)   от­ри­ца­тель­на.

                

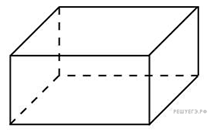
8. Три ребра пря­мо­уголь­но­го па­рал­ле­ле­пи­пе­да, вы­хо­дя­щие из одной вер­ши­ны, равны 1, 4 и 16. Най­ди­те ребро рав­но­ве­ли­ко­го ему куба.

9. Най­ди­те зна­че­ние вы­ра­же­ния .

10. Во­до­лаз­ный ко­ло­кол, со­дер­жа­щий моля воз­ду­ха при дав­ле­нии ат­мо­сфе­ры, мед­лен­но опус­ка­ют на дно водоёма. При этом про­ис­хо­дит изо­тер­ми­че­ское сжа­тие воз­ду­ха до ко­неч­но­го дав­ле­ния . Ра­бо­та, со­вер­ша­е­мая водой при сжа­тии воз­ду­ха, опре­де­ля­ет­ся вы­ра­же­ни­ем , где — по­сто­ян­ная, К — тем­пе­ра­ту­ра воз­ду­ха. Най­ди­те, какое дав­ле­ние (в атм) будет иметь воз­дух в ко­ло­ко­ле, если при сжа­тии воз­ду­ха была со­вер­ше­на ра­бо­та в 6900 Дж.

11. Поезд, дви­га­ясь рав­но­мер­но со ско­ро­стью 60 км/ч, про­ез­жа­ет мимо при­до­рож­но­го стол­ба за 9 се­кунд. Най­ди­те длину по­ез­да в мет­рах.

12. Най­ди­те точку мак­си­му­ма функ­ции .

13. а) Ре­ши­те урав­не­ние

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку

14. В кубе ABCDA₁B₁C₁D₁ все реб­ра равны 1. Най­ди­те рас­сто­я­ние от точки C до пря­мой AD₁

15. Ре­ши­те не­ра­вен­ство:

16. Точка M — се­ре­ди­на сто­ро­ны AD па­рал­ле­ло­грам­ма ABCD . Из вер­ши­ны A про­ве­де­ны два луча, ко­то­рые раз­би­ва­ют от­ре­зок BM на три рав­ные части.

а) До­ка­жи­те, что один из лучей со­дер­жит диа­го­наль па­рал­ле­ло­грам­ма.

б) Най­ди­те пло­щадь четырёхуголь­ни­ка, огра­ни­чен­но­го двумя про­ведёнными лу­ча­ми и пря­мы­ми BD и BC , если пло­щадь па­рал­ле­ло­грам­ма ABCD равна 120.

17. В банк был по­ло­жен вклад под бан­ков­ский про­цент 10%. Через год хо­зя­ин вкла­да снял со счета 2000 руб­лей, а еще через год снова внес 2000 руб­лей. Од­на­ко, вслед­ствие этих дей­ствий через три года со вре­ме­ни пер­во­на­чаль­но­го вло­же­ния вкла­да он по­лу­чил сумму мень­ше за­пла­ни­ро­ван­ной (если бы не было про­ме­жу­точ­ных опе­ра­ций со вкла­дом). На сколь­ко руб­лей мень­ше за­пла­ни­ро­ван­ной суммы по­лу­чил в итоге вклад­чик?

18. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние

    имеет хотя бы один ко­рень.

19. Вин­ти­ки можно раз­ло­жить в па­ке­ти­ки, а па­ке­ти­ки упа­ко­вать в ко­роб­ки, по 3 па­ке­ти­ка в одну ко­роб­ку. Можно эти же вин­ти­ки раз­ло­жить в па­ке­ти­ки так, что в каж­дом па­ке­ти­ке будет на 3 вин­ти­ка боль­ше, чем рань­ше, но тогда в каж­дой ко­роб­ке будет ле­жать по 2 па­ке­ти­ка, а ко­ро­бок по­тре­бу­ет­ся на 2 боль­ше. Какое наи­боль­шее число вин­ти­ков может быть при таких усло­ви­ях?

 

 

Диагностическая работа№2     Профильный уровень                               15.12.2016

ВАРИАНТ№5

1. В книге Елены Мо­ло­хо­вец «По­да­рок мо­ло­дым хо­зяй­кам» име­ет­ся ре­цепт пи­ро­га с чер­но­с­ли­вом. Для пи­ро­га на 10 че­ло­век сле­ду­ет взять     фунта чер­но­сли­ва. Сколь­ко грам­мов чер­но­сли­ва сле­ду­ет взять для пи­ро­га, рас­счи­тан­но­го на 6 че­ло­век. Счи­тай­те, что 1 фунт равен 0,4 кг.

2. На ри­сун­ке жир­ны­ми точ­ка­ми по­ка­за­но су­точ­ное ко­ли­че­ство осад­ков, вы­па­дав­ших в Ка­за­ни с 3 по 15 фев­ра­ля 1909 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся числа ме­ся­ца, по вер­ти­ка­ли — ко­ли­че­ство осад­ков, вы­пав­ших в со­от­вет­ству­ю­щий день, в мил­ли­мет­рах. Для на­гляд­но­сти жир­ные точки на ри­сун­ке со­еди­не­ны ли­ни­ей. Опре­де­ли­те по ри­сун­ку, сколь­ко дней из дан­но­го пе­ри­о­да вы­па­да­ло более 3 мил­ли­мет­ров осад­ков.

  

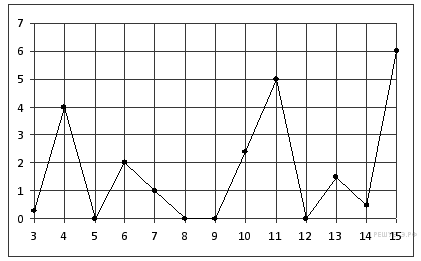
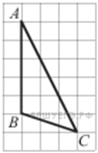
3. На клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1×1 изоб­ражён тре­уголь­ник ABC. Най­ди­те длину его вы­со­ты, опу­щен­ной на сто­ро­ну AB.

 4. Игорь с папой решил по­ка­тать­ся на ко­ле­се обо­зре­ния. Всего на ко­ле­се сорок ка­би­нок, из них 21 – серые, 13 – зе­ле­ные, осталь­ные – крас­ные. Ка­бин­ки по оче­ре­ди под­хо­дят к плат­фор­ме для по­сад­ки. Най­ди­те ве­ро­ят­ность того, что Игорь про­ка­тит­ся в крас­ной ка­бин­ке.

5. Най­ди­те ко­рень урав­не­ния .

6. Пе­ри­метр пря­мо­уголь­ной тра­пе­ции, опи­сан­ной около окруж­но­сти, равен 100, ее боль­шая бо­ко­вая сто­ро­на равна 42. Най­ди­те ра­ди­ус окруж­но­сти.

                

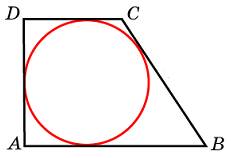
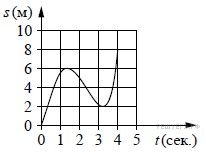
7. Ма­те­ри­аль­ная точка дви­жет­ся от на­чаль­но­го до ко­неч­но­го по­ло­же­ния. На ри­сун­ке изоб­ражён гра­фик её дви­же­ния. На оси абс­цисс от­кла­ды­ва­ет­ся время в се­кун­дах, на оси ор­ди­нат — рас­сто­я­ние от на­чаль­но­го по­ло­же­ния точки (в мет­рах). Най­ди­те сред­нюю ско­рость дви­же­ния точки. Ответ дайте в мет­рах в се­кун­ду.

 

8. Объем тре­уголь­ной пи­ра­ми­ды равен 30. Плос­кость про­хо­дит через сто­ро­ну ос­но­ва­ния этой пи­ра­ми­ды и пе­ре­се­ка­ет про­ти­во­по­лож­ное бо­ко­вое ребро в точке, де­ля­щей его в от­но­ше­нии 7:8, счи­тая от вер­ши­ны пи­ра­ми­ды. Най­ди­те боль­ший из объ­е­мов пи­ра­мид, на ко­то­рые плос­кость раз­би­ва­ет ис­ход­ную пи­ра­ми­ду.

9. Най­ди­те зна­че­ние вы­ра­же­ния      при .

10. Груз мас­сой 0,4 кг ко­леб­лет­ся на пру­жи­не. Его ско­рость v ме­ня­ю­ется по за­ко­ну где — время с мо­мен­та на­ча­ла ко­ле­ба­ний, T = 2 с — пе­ри­од ко­ле­ба­ний, м/с. Ки­не­ти­че­ская энер­гия E (в джо­у­лях) груза вы­чис­ля­ет­ся по фор­му­ле где m — масса груза в ки­ло­грам­мах, v — ско­рость груза в м/с. Най­ди­те ки­не­ти­че­скую энер­гию груза через 36 се­кунд после на­ча­ла ко­ле­ба­ний. Ответ дайте в джо­у­лях.

11. Две трубы на­пол­ня­ют бас­сейн за 48 минут, а одна пер­вая труба на­пол­ня­ет бас­сейн за 1 час. За сколь­ко часов на­пол­ня­ет бас­сейн одна вто­рая труба?

12. Най­ди­те наи­боль­шее зна­че­ние функ­ции        на от­рез­ке .

13. а) Ре­ши­те урав­не­ние         

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку

14. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA₁B₁C₁D₁ из­вест­ны AB = 2, AD = AA₁ = 1. Най­ди­те угол между пря­мой AB₁ и плос­ко­стью ABC₁.

15. Ре­ши­те не­ра­вен­ство .

16. В тре­уголь­ни­ке АВС про­ве­де­ны две вы­со­ты ВМ и CN, причём   и .

а) До­ка­жи­те, что угол АВС тупой.

б) Най­ди­те от­но­ше­ние пло­ща­дей тре­уголь­ни­ков BMN и ABC.

17. По биз­нес-плану пред­по­ла­га­ет­ся вло­жить в четырёхлет­ний про­ект 10 млн руб­лей. По ито­гам каж­до­го года пла­ни­ру­ет­ся при­рост вло­жен­ных средств на 15% по срав­не­нию с на­ча­лом года. На­чис­лен­ные про­цен­ты оста­ют­ся вло­жен­ны­ми в про­ект. Кроме этого, сразу после на­чис­ле­ний про­цен­тов нужны до­пол­ни­тель­ные вло­же­ния: целое число n млн руб­лей в пер­вый и вто­рой годы, а также целое число m млн руб­лей в тре­тий и четвёртый годы.  Най­ди­те наи­мень­шие зна­че­ния n и m, при ко­то­рых пер­во­на­чаль­ные вло­же­ния за два года как ми­ни­мум удво­ят­ся, а за че­ты­ре года как ми­ни­мум утро­ят­ся.

18. Най­ди­те все зна­че­ния па­ра­мет­ра       при каж­дом из ко­то­рых си­сте­ма урав­не­ний     имеет ровно че­ты­ре ре­ше­ния.

19. Най­ди­те все пары на­ту­раль­ных чисел m и n, яв­ля­ю­щи­е­ся ре­ше­ни­я­ми урав­не­ния 3ⁿ − 2^m = 1.

 

 

Диагностическая работа№2     Профильный уровень                               15.12.2016

ВАРИАНТ№6

1. В го­ро­де N живет 1 500 000 жи­те­лей. Среди них 20% детей и под­рост­ков. Среди взрос­лых 35% не ра­бо­та­ет (пен­си­о­не­ры, сту­ден­ты, до­мо­хо­зяй­ки и т. п.). Сколь­ко взрос­лых жи­те­лей ра­бо­та­ет?

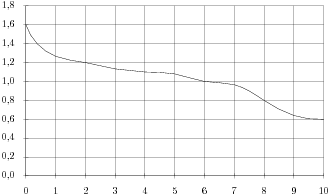
2. При ра­бо­те фо­на­ри­ка ба­та­рей­ка по­сте­пен­но раз­ря­жа­ет­ся, и на­пря­же­ние в элек­три­че­ской цепи фо­на­ри­ка па­да­ет. На ри­сун­ке по­ка­за­на за­ви­си­мость на­пря­же­ния в цепи от вре­ме­ни ра­бо­ты фо­на­ри­ка. На го­ри­зон­таль­ной оси от­ме­ча­ет­ся время ра­бо­ты фо­на­ри­ка в часах, на вер­ти­каль­ной оси — на­пря­же­ние в воль­тах.

Опре­де­ли­те по ри­сун­ку, какое на­пря­же­ние будет в цепи через 2 часа ра­бо­ты фо­на­ри­ка. Ответ дайте в воль­тах.

 

             

 

3. Най­ди­те пло­щадь тра­пе­ции, изоб­ра­жен­ной на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

   4. Кон­курс ис­пол­ни­те­лей про­во­дит­ся в 3 дня. Всего за­яв­ле­но 50 вы­ступ­ле­ний — по од­но­му от каж­дой стра­ны, участ­ву­ю­щей в кон­кур­се. Ис­пол­ни­тель из Рос­сии участ­ву­ет в кон­кур­се. В пер­вый день 18 вы­ступ­ле­ний, осталь­ные рас­пре­де­ле­ны по­ров­ну между остав­ши­ми­ся днями. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что вы­ступ­ле­ние пред­ста­ви­те­ля Рос­сии со­сто­ит­ся в тре­тий день кон­кур­са?

5. Най­ди­те ко­рень урав­не­ния        

6. В тре­уголь­ни­ке    , угол   равен . Най­ди­те вы­со­ту .   

7. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну (где x — рас­сто­я­ние от точки от­сче­та в мет­рах, t — время в се­кун­дах, из­ме­рен­ное с на­ча­ла дви­же­ния). Най­ди­те ее ско­рость в (м/с) в мо­мент вре­ме­ни с.

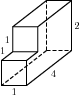
 8. Най­ди­те объем мно­го­гран­ни­ка, изоб­ра­жен­но­го на ри­сун­ке (все дву­гран­ные углы пря­мые).

 

9. Най­ди­те зна­че­ние вы­ра­же­ния         .

 10. Перед от­прав­кой теп­ло­воз издал гудок с ча­сто­той  Гц. Чуть позже издал гудок подъ­ез­жа­ю­щий к плат­фор­ме теп­ло­воз. Из-за эф­фек­та До­пле­ра ча­сто­та вто­ро­го гудка f боль­ше пер­во­го: она за­ви­сит от ско­ро­сти теп­ло­во­за по за­ко­ну 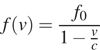 (Гц), где c — ско­рость звука в звука (в м/с). Че­ло­век, сто­я­щий на плат­фор­ме, раз­ли­ча­ет сиг­на­лы по тону, если они от­ли­ча­ют­ся более чем на 3 Гц. Опре­де­ли­те, с какой ми­ни­маль­ной ско­ро­стью при­бли­жал­ся к плат­фор­ме теп­ло­воз, если че­ло­век смог раз­ли­чить сиг­на­лы, а  м/с. Ответ вы­ра­зи­те в м/с.

11. Сме­шав 41-про­цент­ный и 63-про­цент­ный рас­тво­ры кис­ло­ты и до­ба­вив 10 кг чи­стой воды, по­лу­чи­ли 49-про­цент­ный рас­твор кис­ло­ты. Если бы вме­сто 10 кг воды до­ба­ви­ли 10 кг 50-про­цент­но­го рас­тво­ра той же кис­ло­ты, то по­лу­чи­ли бы 54-про­цент­ный рас­твор кис­ло­ты. Сколь­ко ки­ло­грам­мов 41-про­цент­но­го рас­тво­ра ис­поль­зо­ва­ли для по­лу­че­ния смеси?

12. Най­ди­те точку мак­си­му­ма функ­ции .

13. а) Ре­ши­те урав­не­ние        

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку     

14. В пра­виль­ной тре­уголь­ной приз­ме ABCA₁B₁C₁ сто­ро­ны ос­но­ва­ния равны 4, бо­ко­вые рёбра равны 7, точка D — се­ре­ди­на ребра BB₁.

а) Пусть пря­мые C₁D и BC пе­ре­се­ка­ют­ся в точке E. До­ка­жи­те, что угол EAC — пря­мой.

б) Най­ди­те угол между плос­ко­стя­ми ABC и ADC₁.

15. Ре­ши­те не­ра­вен­ство:         

16. В окруж­но­сти про­ве­де­ны хорды PQ и CD, причём PQ = PD = CD = 8, CQ = 6. Най­ди­те CP.

17. В ян­ва­ре 2000 года став­ка по де­по­зи­там в банке «Воз­рож­де­ние» со­ста­ви­ла х % го­до­вых, тогда как в ян­ва­ре 2001 года — у% го­до­вых, при­чем из­вест­но, что x + y = 30%. В ян­ва­ре 2000 года вклад­чик от­крыл счет в банке «Воз­рож­де­ние», по­ло­жив на него не­ко­то­рую сумму. В ян­ва­ре 2001 года, по про­ше­ствии года с того мо­мен­та, вклад­чик снял со счета пятую часть этой суммы. Ука­жи­те зна­че­ние х при ко­то­ром сумма на счету вклад­чи­ка в ян­ва­ре 2002 года ста­нет мак­си­маль­но воз­мож­ной.

18. Най­ди­те все зна­че­ния a, при ко­то­рых любое ре­ше­ние урав­не­ния

    при­над­ле­жит от­рез­ку

19. Най­ди­те все про­стые числа b, для каж­до­го из ко­то­рых су­ще­ству­ет такое целое число а, что дробь можно со­кра­тить на b.

 

 

 

Диагностическая работа№2     Профильный уровень                               15.12.2016

ВАРИАНТ№7

1. На ав­то­за­прав­ке кли­ент отдал кас­си­ру 1000 руб­лей и по­про­сил за­лить бен­зин до пол­но­го бака. Цена бен­зи­на 30 руб. 20 коп. Сдачи кли­ент по­лу­чил 63 руб. 80 коп. Сколь­ко лит­ров бен­зи­на было за­ли­то в бак?

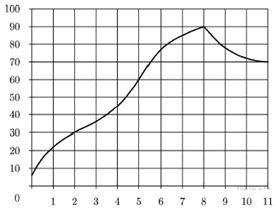
2. На гра­фи­ке по­ка­за­но из­ме­не­ние тем­пе­ра­ту­ры дви­га­те­ля в про­цес­се разо­гре­ва дви­га­те­ля лег­ко­во­го ав­то­мо­би­ля. На оси абс­цисс от­кла­ды­ва­ет­ся время в ми­ну­тах, про­шед­шее от за­пус­ка дви­га­те­ля, на оси ор­ди­нат — тем­пе­ра­ту­ра дви­га­те­ля в гра­ду­сах Цель­сия. Опре­де­ли­те по гра­фи­ку, на сколь­ко гра­ду­сов на­гре­ет­ся дви­га­тель со вто­рой по пятую ми­ну­ту разо­гре­ва.

              

3. Най­ди­те пло­щадь че­ты­рех­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

 4. Кон­курс ис­пол­ни­те­лей про­во­дит­ся в 4 дня. Всего за­яв­ле­но 45 вы­ступ­ле­ний — по од­но­му от каж­дой стра­ны, участ­ву­ю­щей в кон­кур­се. Ис­пол­ни­тель из Рос­сии участ­ву­ет в кон­кур­се. В пер­вый день 18 вы­ступ­ле­ний, осталь­ные рас­пре­де­ле­ны по­ров­ну между остав­ши­ми­ся днями. По­ря­док вы­ступ­ле­ний опре­де­ля­ет­ся же­ребьёвкой. Ка­ко­ва ве­ро­ят­ность, что вы­ступ­ле­ние пред­ста­ви­те­ля Рос­сии со­сто­ит­ся в тре­тий день кон­кур­са?

5. Ре­ши­те урав­не­ние   . Если урав­не­ние имеет более од­но­го корня, в от­ве­те за­пи­ши­те боль­ший из кор­ней.

6. Ос­но­ва­ния тра­пе­ции равны 18 и 6, бо­ко­вая сто­ро­на, рав­ная 7, об­ра­зу­ет с одним из ос­но­ва­ний тра­пе­ции угол 150°. Най­ди­те пло­щадь тра­пе­ции.

7. На ри­сун­ке изоб­ражён гра­фик — про­из­вод­ной функ­ции , опре­делённой на от­рез­ке (−11; 2). Най­ди­те абс­цис­су точки, в ко­то­рой ка­са­тель­ная к гра­фи­ку функ­ции па­рал­лель­на оси абс­цисс или сов­па­да­ет с ней.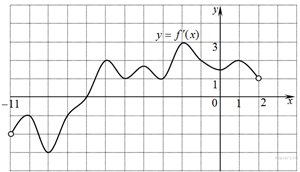                

8. В ци­лин­дри­че­ском со­су­де уро­вень жид­ко­сти до­сти­га­ет 16 см. На какой вы­со­те будет на­хо­дить­ся уро­вень жид­ко­сти, если ее пе­ре­лить во вто­рой сосуд, диа­метр ко­то­ро­го в 2 раза боль­ше пер­во­го? Ответ вы­ра­зи­те в сан­ти­мет­рах.

9. Най­ди­те зна­че­ние вы­ра­же­ния             при .

10. Для сма­ты­ва­ния ка­бе­ля на за­во­де ис­поль­зу­ют лебeдку, ко­то­рая рав­но­уско­рен­но на­ма­ты­ва­ет ка­бель на ка­туш­ку. Угол, на ко­то­рый по­во­ра­чи­ва­ет­ся ка­туш­ка, из­ме­ня­ет­ся со вре­ме­нем по за­ко­ну , где t — время в ми­ну­тах, мин — на­чаль­ная уг­ло­вая ско­рость вра­ще­ния ка­туш­ки, а мин² — уг­ло­вое уско­ре­ние, с ко­то­рым на­ма­ты­ва­ет­ся ка­бель. Ра­бо­чий дол­жен про­ве­рить ход его на­мот­ки не позже того мо­мен­та, когда угол на­мот­ки до­стиг­нет . Опре­де­ли­те время после на­ча­ла ра­бо­ты лебeдки, не позже ко­то­ро­го ра­бо­чий дол­жен про­ве­рить еe ра­бо­ту. Ответ вы­ра­зи­те в ми­ну­тах.

11. Цена хо­ло­диль­ни­ка в ма­га­зи­не еже­год­но умень­ша­ет­ся на одно и то же число про­цен­тов от преды­ду­щей цены. Опре­де­ли­те, на сколь­ко про­цен­тов каж­дый год умень­ша­лась цена хо­ло­диль­ни­ка, если, вы­став­лен­ный на про­да­жу за 20 900 руб­лей, через два года был про­дан за 16 929 руб­лей.

12. Най­ди­те наи­мень­шее зна­че­ние функ­ции на от­рез­ке .

13. Ре­ши­те урав­не­ние

14. Дан куб ABCDA₁B₁C₁D₁. Длина ребра куба равна 1. Най­ди­те рас­сто­я­ние от се­ре­ди­ны от­рез­ка BC₁ до плос­ко­сти AB₁D₁.

15. Ре­ши­те не­ра­вен­ство:

16. В тре­уголь­ни­ке из­вест­ны сто­ро­ны: . Окруж­ность, про­хо­дя­щая через точки и , пе­ре­се­ка­ет пря­мые и со­от­вет­ствен­но в точ­ках и , от­лич­ных от вер­шин тре­уголь­ни­ка. От­ре­зок ка­са­ет­ся окруж­но­сти, впи­сан­ной в тре­уголь­ник . Най­ди­те длину от­рез­ка .

17. В июле 2016 года пла­ни­ру­ет­ся взять кре­дит в банке в раз­ме­ре S тыс. руб­лей, где S — на­ту­раль­ное число, на 3 года. Усло­вия его воз­вра­та та­ко­вы

− каж­дый ян­варь долг уве­ли­чи­ва­ет­ся на 15% по срав­не­нию с кон­цом преды­ду­ще­го года;

− с фев­ра­ля по июнь каж­до­го года не­об­хо­ди­мо вы­пла­тить одним пла­те­жом часть долга;

− в июле каж­до­го года долг дол­жен со­став­лять часть кре­ди­та в со­от­вет­ствии со сле­ду­ю­щей таб­ли­цей.

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019
Долг (в тыс. руб­лей)	S	0,7S	0,4S	0

 Най­ди­те наи­мень­шее зна­че­ние S, при ко­то­ром каж­дая из вы­плат будет со­став­лять целое число тысяч руб­лей.

18. Най­ди­те все зна­че­ния па­ра­мет­ра a, при ко­то­рых урав­не­ние имеет един­ствен­ное ре­ше­ние.

19. Мно­же­ство чисел назовём хо­ро­шим, если его можно раз­бить на два под­мно­же­ства с оди­на­ко­вой сум­мой чисел.

а) Яв­ля­ет­ся ли мно­же­ство {200; 201; 202; ...; 299} хо­ро­шим?

б) Яв­ля­ет­ся ли мно­же­ство {2; 4; 8; ...; 2¹⁰⁰} хо­ро­шим?

в) Сколь­ко хо­ро­ших четырёхэле­мент­ных под­мно­жеств у мно­же­ства {1; 2; 4; 5; 7; 9; 11}?

 

 

Диагностическая работа№2        Профильный уровень                           15.12.2016

ВАРИАНТ№8

1. В доме, в ко­то­ром живет Катя, 9 эта­жей и не­сколь­ко подъ­ез­дов. На каж­дом этаже на­хо­дит­ся по 4 квар­ти­ры. Катя живет в квар­ти­ре № 63. В каком подъ­ез­де живет Катя?

2. На диа­грам­ме по­ка­за­на сред­не­ме­сяч­ная тем­пе­ра­ту­ра воз­ду­ха в Сим­фе­ро­по­ле за каж­дый месяц 1988 года. По го­ри­зон­та­ли ука­зы­ва­ют­ся ме­ся­цы, по вер­ти­ка­ли — тем­пе­ра­ту­ра в гра­ду­сах Цель­сия. Опре­де­ли­те по диа­грам­ме, сколь­ко было ме­ся­цев, когда сред­не­ме­сяч­ная тем­пе­ра­ту­ра пре­вы­ша­ла 20 гра­ду­сов Цель­сия.

       

3. Най­ди­те пло­щадь тре­уголь­ни­ка, изоб­ра­жен­но­го на клет­ча­той бу­ма­ге с раз­ме­ром клет­ки 1 см 1 см (см. рис.). Ответ дайте в квад­рат­ных сан­ти­мет­рах.

4. В тор­го­вом цен­тре два оди­на­ко­вых ав­то­ма­та про­да­ют кофе. Об­слу­жи­ва­ние ав­то­ма­тов про­ис­хо­дит по ве­че­рам после за­кры­тия цен­тра. Из­вест­но, что ве­ро­ят­ность со­бы­тия «К ве­че­ру в пер­вом ав­то­ма­те за­кон­чит­ся кофе» равна 0,25. Такая же ве­ро­ят­ность со­бы­тия «К ве­че­ру во вто­ром ав­то­ма­те за­кон­чит­ся кофе». Ве­ро­ят­ность того, что кофе к ве­че­ру за­кон­чит­ся в обоих ав­то­ма­тах, равна 0,15. Най­ди­те ве­ро­ят­ность того, что к ве­че­ру дня кофе оста­нет­ся в обоих ав­то­ма­тах.

5. Ре­ши­те урав­не­ние        

6. В тре­уголь­ни­ке  угол равен , , 3,  — вы­со­та. Най­ди­те .                     

7. Ма­те­ри­аль­ная точка дви­жет­ся пря­мо­ли­ней­но по за­ко­ну    где х — рас­сто­я­ние от точки отсчёта (в мет­рах), t — время дви­же­ния (в се­кун­дах). Най­ди­те её ско­рость (в мет­рах в се­кун­ду) в мо­мент вре­ме­ни t = 6 с.

8. На ри­сун­ке изоб­ражён мно­го­гран­ник, все дву­гран­ные углы мно­го­гран­ни­ка пря­мые. Най­ди­те квад­рат рас­сто­я­ния между вер­ши­на­ми и .

9. Най­ди­те зна­че­ние вы­ра­же­ния         .

10. Для на­гре­ва­тель­но­го эле­мен­та не­ко­то­ро­го при­бо­ра экс­пе­ри­мен­таль­но была по­лу­че­на за­ви­си­мость тем­пе­ра­ту­ры (в кель­ви­нах) от вре­ме­ни ра­бо­ты: T(t) = T₀ + bt + at² , где t — время в ми­ну­тах, T₀ = 1380 К, а = −15 К/мин², b= 165 К/мин. Из­вест­но, что при тем­пе­ра­ту­ре на­гре­ва­те­ля свыше 1800 К при­бор может ис­пор­тить­ся, по­это­му его нужно от­клю­чить. Опре­де­ли­те, через какое наи­боль­шее время после на­ча­ла ра­бо­ты нужно от­клю­чить при­бор. Ответ вы­ра­зи­те в ми­ну­тах.

11. Пер­вые 120 км ав­то­мо­биль ехал со ско­ро­стью 90 км/ч, сле­ду­ю­щие 100 км — со ско­ро­стью 100 км/ч, а затем 110 км — со ско­ро­стью 110 км/ч. Най­ди­те сред­нюю ско­рость ав­то­мо­би­ля на про­тя­же­нии всего пути. Ответ дайте в км/ч.

12. Най­ди­те наи­мень­шее зна­че­ние функ­ции         на от­рез­ке

13. а) Ре­ши­те урав­не­ние        .

б) Ука­жи­те корни этого урав­не­ния, при­над­ле­жа­щие про­ме­жут­ку .

14. В пра­виль­ной четырёхуголь­ной приз­ме ABCDA₁B₁C₁D₁ сто­ро­на ос­но­ва­ния AB=6, а бо­ко­вое ребро На рёбрах AB, A₁D₁ и C₁D₁ от­ме­че­ны точки M, N и K со­от­вет­ствен­но, причём AM = A₁N = C₁K = 1.

а) Пусть L — точка пе­ре­се­че­ния плос­ко­сти MNK с реб­ром BC. До­ка­жи­те, что MNKL — квад­рат.

б) Най­ди­те пло­щадь се­че­ния приз­мы плос­ко­стью MNK.

15. Ре­ши­те не­ра­вен­ство:      

16. Окруж­ность ра­ди­у­са впи­са­на в пря­мой угол. Вто­рая окруж­ность также впи­са­на в этот угол и пе­ре­се­ка­ет­ся с пер­вой в точ­ках M и N. Из­вест­но, что рас­сто­я­ние между цен­тра­ми окруж­но­стей равно 6. Най­ди­те MN.

17. В июле 2016 года пла­ни­ру­ет­ся взять кре­дит в банке на пять лет в раз­ме­ре S тыс руб­лей. Усло­вия его воз­вра­та та­ко­вы:

− каж­дый ян­варь долг воз­рас­та­ет на 20% по срав­не­нию с кон­цом преды­ду­ще­го года;

− с фев­ра­ля по июнь каж­до­го года не­об­хо­ди­мо вы­пла­тить часть долга;

− в июле 2017,2018 и 2019 долг остаётся рав­ным S тыс. руб­лей;

− вы­пла­ты в 2020 и 2021 годах равны по 360 тыс. руб­лей;

− к июлю 2021 долг будет вы­пла­чен пол­но­стью.

Най­ди­те общую сумму вы­плат за пять лет.

18. Най­ди­те все зна­че­ния па­ра­мет­ра при каж­дом из ко­то­рых си­сте­ма

           имеет ровно          ре­ше­ний.

19. Най­ди­те все трой­ки на­ту­раль­ных чисел k, m и n, удо­вле­тво­ря­ю­щие урав­не­нию

 

 

Ответы   ключи

Вариант№1                          Вариант№2            Вариант№3              Вариант№4

1	13	1	18	1	32,4	1	26
2	200	2	3	2	29,4	2	2
3	21	3	6	3	8	3	4
4	0,16	4	0,275	4	0,4	4	0,2
5	-4	5	3,75	5	2	5	1
6	8	6	60	6	6	6	7
7	4	7	-18	7	6	7	8
8	0,3	8	24	8	9	8	4
9	-22	9	-2	9	-28	9	16
10	400	10	88	10	30	10	6
11	42	11	12	11	8	11	150
12	1,5	12	-4	12	-6	12	-10

 Вариант№5                         Вариант№6            Вариант№7              Вариант№8

1	72	1	780000	1	31	1	2
2	3	2	1,2	2	32	2	2
3	3	3	3	3	2,5	3	2,5
4	0;15	4	0,32	4	0,2	4	0,65
5	-42	5	6	5	-3	5	3
6	4	6	2	6	42	6	1,8
7	4	7	59	7	-7	7	72
8	16	8	7	8	4	8	11
9	15	9	20	9	144	9	25
10	0,072	10	3,5	10	20	10	4
11	4	11	35	11	10	11	99
12	295	12	-15	12	0	12	-13

 

 

Ответы вариант№1

13. а) Ре­ши­те урав­не­ние

б) Ука­жи­те корни урав­не­ния, при­над­ле­жа­щие от­рез­ку

Ре­ше­ние.

а) По фор­му­ле при­ве­де­ния и фор­му­ле ко­си­ну­са двой­но­го угла:

Тогда или От­ку­да или

б) С по­мо­щью еди­нич­ной окруж­но­сти отберём корни на от­рез­ке Это числа и (см. рис.).

Ответ:

а)     б)

14. В пра­виль­ной тре­уголь­ной приз­ме ABCA₁B₁C₁, все рёбра ко­то­рой равны 1, най­ди­те рас­сто­я­ние между пря­мы­ми AA₁ и BC₁.

Так как пря­мая пе­ре­се­ка­ет­ся с пря­мой па­рал­лель­ной пря­мой и лежит в плос­ко­сти па­рал­лель­ной то рас­сто­я­ние между пря­мы­ми и равно рас­сто­я­нию от пря­мой до плос­ко­сти

 

Пусть  — вы­со­та тре­уголь­ни­ка пер­пен­ди­ку­ляр­на грани так как пер­пен­ди­ку­ляр­на двум пе­ре­се­ка­ю­щим­ся пря­мым ( и ), ле­жа­щим в плос­ко­сти Таким об­ра­зом, ис­ко­мое рас­сто­я­ние — длина от­рез­ка Из рав­но­сто­рон­не­го тре­уголь­ни­ка на­хо­дим:

 .         Ответ: .

15. Ре­ши­те не­ра­вен­ство:

Ре­ше­ние.Решим пер­вое не­ра­вен­ство си­сте­мы. Сде­ла­ем за­ме­ну .

 

Тогда , от­ку­да на­хо­дим ре­ше­ние пер­во­го не­ра­вен­ства си­сте­мы:

 Ответ:

16. Внев­пи­сан­ной окруж­но­стью тре­уголь­ни­ка на­зы­ва­ет­ся окруж­ность, ка­са­ю­ща­я­ся одной сто­ро­ны тре­уголь­ни­ка и про­дол­же­ний двух дру­гих его сто­рон. Ра­ди­у­сы двух внев­пи­сан­ных окруж­но­стей пря­мо­уголь­но­го тре­уголь­ни­ка равны 1 и 7. Най­ди­те рас­сто­я­ние между их цен­тра­ми.

Ре­ше­ние.Рас­смот­рим пря­мо­уголь­ный тре­уголь­ник с ка­те­та­ми и ги­по­те­ну­зой Пусть окруж­ность с цен­тром ра­ди­у­са ка­са­ет­ся ги­по­те­ну­зы в точке про­дол­же­ний ка­те­тов и − в точ­ках и со­от­вет­ствен­но, а − по­лу­пе­ри­метр тре­уголь­ни­ка Из ра­вен­ства от­рез­ков ка­са­тель­ных, про­ве­ден­ных к окруж­но­сти из одной точки, сле­ду­ет, что и по­это­му

  

               

а так как , то Далее, пусть окруж­ность с цен­тром ра­ди­у­са ка­са­ет­ся ка­те­та в точке а про­дол­же­ний сто­рон и − в точка и со­от­вет­ствен­но. Рас­суж­дая ана­ло­гич­но, по­лу­ча­ем Че­ты­рех­уголь­ни­ки и − квад­ра­ты, по­это­му

    зна­чит,

Сле­до­ва­тель­но, ра­ди­ус внев­пи­сан­ной окруж­но­сти, ка­са­ю­щей­ся ги­по­те­ну­зы дан­но­го пря­мо­уголь­но­го тре­уголь­ни­ка, не может быть равен 1.

Таким об­ра­зом, воз­мож­ны толь­ко такие слу­чаи: Либо ра­ди­ус окруж­но­сти, ка­са­ю­щей­ся ги­по­те­ну­зы, равен 7, а ра­ди­ус окруж­но­сти, ка­са­ю­щей­ся од­но­го из ка­те­тов, равен 1, либо ра­ди­у­сы окруж­но­стей, ка­са­ю­щих­ся ка­те­тов, равны 1 и 7.

Пред­по­ло­жим, что и (рис. 1).

Опу­стим пер­пен­ди­ку­ляр из цен­тра мень­шей окруж­но­сти на Тогда

 

 

 

Сле­до­ва­тель­но,            

 Пусть те­перь и (рис 2)

Центр окруж­но­сти, впи­сан­ной в угол, лежит на бис­сек­три­се угла, по­это­му точки и лежат на оной пря­мой. Сле­до­ва­тель­но,

 

 Ответ: или

17. Из­вест­но, что вклад, на­хо­дя­щий­ся в банке с на­ча­ла года, воз­рас­та­ет к концу года на опре­де­лен­ный про­цент, свой для каж­до­го банка. В на­ча­ле года Сте­пан по­ло­жил 60% не­ко­то­рой суммы денег в пер­вый банк, а остав­шу­ю­ся часть суммы во вто­рой банк. К концу года сумма этих вкла­дов стала равна 590 000 руб., а к концу сле­ду­ю­ще­го года 701 000 руб. Если бы Сте­пан пер­во­на­чаль­но по­ло­жил 60% своей суммы во вто­рой банк, а остав­шу­ю­ся часть в пер­вый, то по ис­те­че­нии од­но­го года сумма вкла­дов стала бы рав­ной 610 000 руб. Ка­ко­ва была бы сумма вкла­дов в этом слу­чае к концу вто­ро­го года?

Ре­ше­ние.

Пусть у Сте­па­на было х тыс. руб., пер­вый банк дает а% го­до­вых, вто­рой — b% го­до­вых. Тогда в конце года сумма вкла­да в пер­вом банке уве­ли­чит­ся в раз, а во вто­ром банке в раз.

Сте­пан по­ло­жил в пер­вый и вто­рой банк 60% и 40% сво­е­го ка­пи­та­ла, по про­ше­ствии од­но­го года на сче­тах в бан­ках было тыс. руб. со­от­вет­ствен­но. Если бы Сте­пан пер­во­на­чаль­но по­ло­жил 40% ка­пи­та­ла в пер­вый банк, а 60% ка­пи­та­ла во вто­рой банк, то через год на сче­тах было бы тыс. руб.

Решая си­сте­му урав­не­ний

от­но­си­тель­но xm и xn на­хо­дим:

К концу вто­ро­го года сумма вкла­дов до­стиг­ла ве­ли­чи­ны

 

По усло­вию, она равна 701 тыс. руб., от­ку­да имеем:      

 

Тогда а ис­ко­мая ве­ли­чи­на суммы вкла­да к концу вто­ро­го года при вло­же­нии 40% ка­пи­та­ла в пер­вый банк и 60% во вто­рой равна

 

тыс. руб.

Ответ: 749 000 руб.

18. Най­ди­те все зна­че­ния а, при каж­дом из ко­то­рых ре­ше­ния не­ра­вен­ства об­ра­зу­ют от­ре­зок длины 1.

Ре­ше­ние.

Пе­ре­не­сем двой­ку:

По­стро­им схе­ма­тич­но гра­фи­ки функ­ций и

На ри­сун­ке видно, что не­ра­вен­ство имеет ре­ше­ния толь­ко при или

1)

Ре­ше­ния об­ра­зу­ют от­ре­зок длины 1, если от­ку­да

2)

Ре­ше­ния об­ра­зу­ют от­ре­зок длины 1, если от­ку­да

 

Ответ:

19. На доске на­пи­са­ли не­сколь­ко не обя­за­тель­но раз­лич­ных дву­знач­ных на­ту­раль­ных чисел без нулей в де­ся­тич­ной за­пи­си. Сумма этих чисел ока­за­лась рав­ной 2970. В каж­дом числе по­ме­ня­ли ме­ста­ми первую и вто­рую цифры (на­при­мер, число 16 за­ме­ни­ли на число 61).

а) При­ве­ди­те при­мер ис­ход­ных чисел, для ко­то­рых сумма по­лу­чив­ших­ся чисел ровно в 3 раза мень­ше, чем сумма ис­ход­ных чисел.

б) Могла ли сумма по­лу­чив­ших­ся чисел быть ровно в 5 раз мень­ше, чем сумма ис­ход­ных чисел?

в) Най­ди­те наи­мень­шее воз­можн­ное зна­че­ние суммы по­лу­чив­шиъ­ся чисел.

Ре­ше­ние.

Пусть ис­ход­ные числа равны и пусть суммы цифр, сто­я­щих в раз­ря­де еди­ниц и де­сят­ков, со­от­вет­ствен­но и

а) Решим си­сте­му урав­не­ний: 

При­ме­ром ис­ход­но­го на­бо­ра чисел может быть 70 дву­знач­ных чисел, за­кан­чи­ва­ю­щих­ся еди­ни­цей, сумма де­сят­ков ко­то­рых дает 290. На­при­мер, это 68 чисел 41 и два числа 91 или 50 чисел 51 и 20 чисел 21. Ещё при­мер (его можно по­стро­ить, об­ра­тив вни­ма­ние, что сумма де­сят­ков при­мер­но в 4 раза боль­ше суммы еди­ниц): 32 раза число 92 и число 26.

б) Решим си­сте­му урав­не­ний: 

 

По­сколь­ку нулей в за­пи­си чисел нет, сумма цифр, сто­я­щих в раз­ря­де еди­ниц, не мень­ше ко­ли­че­ства чисел. Тем самым, чисел не боль­ше 30. Но тогда сумма цифр, сто­я­щих в раз­ря­де де­сят­ков, не может быть боль­ше 270. Про­ти­во­ре­чие.

Иначе: по­сколь­ку в за­пи­си нет нулей, а цифры в раз­ря­де де­сят­ков не пре­вы­ша­ют 9, спра­вед­ли­вы со­от­но­ше­ния: то есть что про­ти­во­ре­чит по­лу­чен­ной си­сте­ме, в ко­то­рой

в) Тре­бу­ет­ся опре­де­лить, для ка­ко­го наи­мень­ше­го S имеет ре­ше­ния си­сте­ма урав­не­ний

 

 

Из по­лу­чен­ной си­сте­мы сле­ду­ет, что ве­ли­чи­на S крат­на 9 и 11 то есть крат­на 99. Тогда Тогда

Наи­мень­ше­му зна­че­нию со­от­вет­ству­ет наи­мень­шее зна­че­ние при­чем из вто­ро­го урав­не­ния си­сте­мы ясно, что Улуч­шим оцен­ку: за­ме­тим, что от­ку­да тогда

 

и, тем самым,

Если то: за­дан­ным на­бо­ром чисел, на­при­мер, яв­ля­ют­ся 30 чисел 91, 9 чисел 21 и число 51, сумма чисел в на­бо­ре равна

 

Ответ: а) на­при­мер, 32 раза число 92 и число 26, б) нет, в) 693.

Вариант№2

13. а) Ре­ши­те урав­не­ние

б) Ука­жи­те корни этого урав­не­ния, при­над­ле­жа­ще­го от­рез­ку

Ре­ше­ние.

а) За­пи­шем ис­ход­ное урав­не­ние в виде:

 

 

Урав­не­ние кор­ней не имеет. Зна­чит, от­ку­да или

б) С по­мо­щью чис­ло­вой окруж­но­сти отберём корни, при­над­ле­жа­щие от­рез­ку По­лу­чим число

Ответ: а) б)

14. В пра­виль­ной че­ты­рех­уголь­ной приз­ме KLMNK₁L₁M₁N₁ точка E делит бо­ко­вое ребро KK₁ в от­но­ше­нии KE : EK₁ = 1 : 3. Через точки L и E про­ве­де­на плос­кость па­рал­лель­ная пря­мой KM и пе­ре­се­ка­ю­щая ребро NN₁ в точке F.

а) До­ка­жи­те, что плос­кость делит ребро NN₁ по­по­лам.

б) Най­ди­те угол между плос­ко­стью и плос­ко­стью грани KLMN, если из­вест­но, что KL = 6 , KK₁ = 4 .

Ре­ше­ние.

Пусть четырёхуголь­ник ELGF — се­че­ние дан­ной приз­мы плос­ко­стью α (см. ри­су­нок). Пря­мая KM па­рал­лель­на плос­ко­сти α, а плос­кость KMG пе­ре­се­ка­ет плос­кость α по пря­мой EG, сле­до­ва­тель­но EG || KM и, зна­чит, KMGE — пря­мо­уголь­ник. Пря­мые NL и KM яв­ля­ют­ся со­от­вет­ствен­но про­ек­ци­я­ми пря­мых FL и EG на плос­кость KLM, зна­чит, точка пе­ре­се­че­ния пря­мых KM и NL (точка H) яв­ля­ет­ся про­ек­ци­ей точки пе­ре­се­че­ния пря­мых FL и EG (точки O) на эту плос­кость. Таким

об­ра­зом, C дру­гой сто­ро­ны, от­ре­зок OH — сред­няя линия тре­уголь­ни­ка FLN и, сле­до­ва­тель­но, от­ку­да и сле­ду­ет до­ка­зы­ва­е­мое утвер­жде­ние.

б) Пусть точка D ― се­ре­ди­на от­рез­ка FN. Тогда EK = FD и EK || FD, сле­до­ва­тель­но, EKDF ― па­рал­ле­ло­грамм и, зна­чит, EF || KD. Так как и EG || KM , то (KDM) || (EFG) и, зна­чит, По­сколь­ку KLMN ― квад­рат, то NH ⊥ KM, но тогда, со­глас­но тео­ре­ме о трех пер­пен­ди­ку­ля­рах, и DH ⊥ KM. Таким об­ра­зом, ― ли­ней­ный угол дву­гран­но­го угла . Из пря­мо­уголь­но­го тре­уголь­ни­ка DNH на­хо­дим

 

Ответ: б)

15. Ре­ши­те не­ра­вен­ство:

Ре­ше­ние.

После за­ме­ны по­лу­ча­ем Зна­чит,

 

     или     

 

Решим первую си­сте­му не­ра­венств:

 

Воз­вра­ща­ясь к ис­ход­ной пе­ре­мен­ной, по­лу­ча­ем:

 Решим вто­рую си­сте­му не­ра­венств: 

Воз­вра­ща­ясь к ис­ход­ной пе­ре­мен­ной, по­лу­ча­ем:

 Таким об­ра­зом, ре­ше­ни­ем ис­ход­но­го не­ра­вен­ства яв­ля­ет­ся мно­же­ство

Ответ:

16. Точка M лежит на от­рез­ке AB. На окруж­но­сти с диа­мет­ром AB взята точка C, уда­лен­ная от точек A, M и B на рас­сто­я­ния 20, 14 и 15 со­от­вет­ствен­но. Най­ди­те пло­щадь тре­уголь­ни­ка BMC.

Ре­ше­ние.

                 

Точка лежит на окруж­но­сти с диа­мет­ром по­это­му По тео­ре­ме Пи­фа­го­ра

 

Пусть — вы­со­та тре­уголь­ни­ка Тогда: .

Из пря­мо­уголь­но­го тре­уголь­ни­ка на­хо­дим:

 

Если точка лежит между точ­ка­ми и , то

Сле­до­ва­тель­но,

 

Если точка лежит между и то Сле­до­ва­тель­но,

 

Ответ:

17. В банк был по­ло­жен вклад под бан­ков­ский про­цент 10%. Через год хо­зя­ин вкла­да снял со счета 2000 руб­лей, а еще через год снова внес 2000 руб­лей. Од­на­ко, вслед­ствие этих дей­ствий через три года со вре­ме­ни пер­во­на­чаль­но­го вло­же­ния вкла­да он по­лу­чил сумму мень­ше за­пла­ни­ро­ван­ной (если бы не было про­ме­жу­точ­ных опе­ра­ций со вкла­дом). На сколь­ко руб­лей мень­ше за­пла­ни­ро­ван­ной суммы по­лу­чил в итоге вклад­чик?

За­да­ние 17 № 508585

Ре­ше­ние.

Пусть вклад­чик в банк пер­во­на­чаль­но по­ло­жил х руб. Тогда за 3 года хра­не­ния этих денег вклад вырос бы до 1,331 х р, т. е. до р.

За пер­вый год хра­не­ния вкла­да он вырос до 1,1 р. Од­на­ко, через год вклад­чик снял 2000 р. На счету оста­лось р. В конце вто­ро­го года хра­не­ния вкла­да на эту сумму были на­чис­ле­ны про­цен­ты, вклад стал р. Од­на­ко, вклад­чик снова внес 2000 р. Сумма вкла­да стала р.

К концу тре­тье­го года хра­не­ния вкла­да ее сумма стала

 

 

И эту сумму снял вклад­чик в итоге вме­сто пер­во­на­чаль­но за­пла­ни­ро­ван­ной р.

Най­дем ис­ко­мую раз­ность.

 

 

Ответ: на 220 р.

18. Най­ди­те все по­ло­жи­тель­ные зна­че­ния а, при каж­дом из ко­то­рых си­сте­ма имеет един­ствен­ное ре­ше­ние.

За­да­ние 18 № 507190

Ре­ше­ние.

Если , то урав­не­ние задаёт окруж­ность , с цен­тром в точке ра­ди­у­са 2, а если , то оно задаёт окруж­ность с цен­тром в точке того же ра­ди­у­са (см. рис.).

 

При по­ло­жи­тель­ных зна­че­ни­ях па­ра­мет­ра а урав­не­ние за­да­ет окруж­ность с цен­тром в точке ра­ди­у­са а. По­это­му за­да­ча со­сто­ит в том, чтобы найти все зна­че­ния па­ра­мет­ра а, при каж­дом из ко­то­рых окруж­ность имеет един­ствен­ную общую точку с объ­еди­не­ни­ем окруж­но­стей и .

 

Из точки С про­ведём луч и обо­зна­чим и точки его пе­ре­се­че­ния с окруж­но­стью , где лежит между С и .

Так как , то  , .

 

При или окруж­но­сти и не пе­ре­се­ка­ют­ся. При окруж­но­сти и имеют две общие точки. При или окруж­но­сти и ка­са­ют­ся.

Из точки С про­ведём луч и обо­зна­чим и точки его пе­ре­се­че­ния с окруж­но­стью , где лежит между С и .

 Так как , то    , .

При или окруж­но­сти и не пе­ре­се­ка­ют­ся. При окруж­но­сти и имеют две общие точки. При или окруж­но­сти и ка­са­ют­ся.

Ис­ход­ная си­сте­ма имеет един­ствен­ное ре­ше­ние тогда и толь­ко тогда, когда окруж­ность ка­са­ет­ся ровно одной из двух окруж­но­стей и , и не пе­ре­се­ка­ет­ся с дру­гой. Так как , то усло­вию за­да­чи удо­вле­тво­ря­ют толь­ко числа и .

 Ответ: 11; .

19. В игре «Дро­ти­ки» есть 20 на­руж­ных сек­то­ров, про­ну­ме­ро­ван­ных от 1 до 20 и два цен­траль­ных сек­то­ра. При по­па­да­нии в на­руж­ный сек­тор игрок по­лу­ча­ет ко­ли­че­ство очков, сов­па­да­ю­щее с но­ме­ром сек­то­ра, а за по­па­да­ние в цен­траль­ные сек­то­ра он по­лу­ча­ет 25 или 50 очков со­от­вет­ствен­но. В каж­дом из на­руж­ных сек­то­ров есть об­ла­сти удво­е­ния и утро­е­ния, ко­то­рые, со­от­вет­ствен­но, удва­и­ва­ют или утра­и­ва­ют но­ми­нал сек­то­ра. Так, на­при­мер, по­па­да­ние в сек­тор 10 (не в зоны удво­е­ния и утро­е­ния) дает 10 очков, в зону удво­е­ния сек­то­ра ― 20 очков, в зону утро­е­ния ― 30 очков.

а) Может ли игрок тремя брос­ка­ми на­брать ровно 167 очков?

б) Может ли игрок ше­стью брос­ка­ми на­брать ровно 356 очков?

в) С по­мо­щью ка­ко­го наи­мень­ше­го ко­ли­че­ства брос­ков, игрок может на­брать ровно 1001 очко?

За­да­ние 19 № 509048

Ре­ше­ние.

а) Да, на­при­мер, при по­па­да­нии в утро­е­ние сек­то­ра 20, утро­е­ние сек­то­ра 19 и цен­траль­ный сек­тор 50 по­лу­ча­ем: 60 + 57 + 50 = 167.

б) Наи­боль­шее ко­ли­че­ство очков, ко­то­рое может на­брать игрок одним брос­ком ― 60 (утро­е­ние 20), далее идут: 57 очков (утро­е­ние 19) и 54 очка (утро­е­ние 18). По­па­да­ние во все осталь­ные сек­то­ра и зоны дает мень­ше 54 очков. Если все шесть брос­ков были по 60 очков, то игрок на­брал 360 очков, что боль­ше 356. Если хотя бы один бро­сок на 60 очков за­ме­нить брос­ком на 54 очка или мень­ше, то сумма умень­шит­ся как ми­ни­мум на 6, а, зна­чит, ста­нет не боль­ше 354 очков, что мень­ше 356 очков. Сле­до­ва­тель­но, бро­сок на 60 очков можно за­ме­нять толь­ко брос­ком на 57 очков. Но одна такая за­ме­на дает ито­го­вый ре­зуль­тат 357 очков, а хотя бы две за­ме­ны ― не более 354 очков. Зна­чит, 356 очков ше­стью брос­ка­ми на­брать не­воз­мож­но.

в) Как было по­ка­за­но в пунк­те б) каж­дый бро­сок при­но­сит иг­ро­ку не более 60 очков. Зна­чит, за 16 брос­ков он на­бе­рет не более 960 очков, а тогда для того, чтобы на­брать 1001 очко по­на­до­бит­ся не менее 17 брос­ков.

По­ка­жем, что игрок может на­брать 1001 очко за 17 брос­ков. Пред­по­ло­жим, что он сде­лал 15 брос­ков на 60 очков (итого 900), один бро­сок в зону утро­е­ния сек­то­ра 17 (51 очко) и один бро­сок в цен­траль­ный сек­тор 50 очков. Тогда в сумме он на­бе­рет 900 + 51 + 50 = 1001 очко.

 

Ответ: а) да; б) нет; в) за 17 брос­ков.

Вариант№3

13. а) Ре­ши­те урав­не­ние

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку

За­да­ние 13 № 514526

Ре­ше­ние.

а) Пусть тогда ис­ход­ное урав­не­ние за­пи­шет­ся в виде от­ку­да или

При по­лу­чим: зна­чит, что не­воз­мож­но.

При по­лу­чим: зна­чит, от­ку­да

б) C по­мо­щью чис­ло­вой окруж­но­сти отберём корни, при­над­ле­жа­щие от­рез­ку

По­лу­чим число:

Ответ: а) б)

14. Все рёбра пра­виль­ной тре­уголь­ной пи­ра­ми­ды SBCD с вер­ши­ной S равны 9.

Ос­но­ва­ние O вы­со­ты SO этой пи­ра­ми­ды яв­ля­ет­ся се­ре­ди­ной от­рез­ка SS₁, M — се­ре­ди­на ребра SB , точка L лежит на ребре CD так, что CL : LD = 7 : 2.

а) До­ка­жи­те, что се­че­ние пи­ра­ми­ды SBCD плос­ко­стью S₁LM — рав­но­бо­кая тра­пе­ция.

б) Вы­чис­ли­те длину сред­ней линии этой тра­пе­ции.

За­да­ние 14 № 512357

Ре­ше­ние.

Про­ведём ме­ди­а­ну S₁M тре­уголь­ни­ка SS₁B, ко­то­рая пе­ре­се­ка­ет ме­ди­а­ну BB₁ ос­но­ва­ния BCD в точке T. Тогда ВТ : ТВ₁ = 4 : 5, по­сколь­ку BB₁ также яв­ля­ет­ся ме­ди­а­ной тре­уголь­ни­ка SS₁B.

Точка L, в свою оче­редь, делит от­ре­зок B₁D в от­но­ше­нии DL : LВ₁ = 4 : 5, так как LD : LC = 2 : 7 и от­ре­зок BB₁ — ме­ди­а­на тре­уголь­ни­ка BCD.

Сле­до­ва­тель­но, сто­ро­на се­че­ния, про­хо­дя­щая через точки L и T, па­рал­лель­на сто­ро­не BD ос­но­ва­ния BCD. Пусть пря­мая LT пе­ре­се­ка­ет BC в точке P.

Про­ведём через точку M сред­нюю линию в тре­уголь­ни­ке SBD, пусть она пе­ре­се­ка­ет сто­ро­ну SD в точке K. Тогда PMKL — ис­ко­мое се­че­ние, причём BP = DL и BM = KD. Из ра­вен­ства тре­уголь­ни­ков BMP и DKL по­лу­чим MP = KL, а зна­чит, PMKL — рав­но­бо­кая тра­пе­ция.

б) Боль­шее ос­но­ва­ние PL тра­пе­ции равно 7, по­сколь­ку тре­уголь­ник LPC пра­виль­ный. Вто­рое ос­но­ва­ние MK равно 4,5, по­сколь­ку MK — сред­няя линия пра­виль­но­го тре­уголь­ни­ка SBD. Сле­до­ва­тель­но, сред­няя линия тра­пе­ции равна

 

Ответ: 5,75.

15. Ре­ши­те не­ра­вен­ство:

За­да­ние 15 № 511554

Ре­ше­ние.

Имеем:

 

Ответ:

16. В тре­уголь­ни­ке из­вест­ны сто­ро­ны: Окруж­ность, про­хо­дя­щая через точки и пе­ре­се­ка­ет пря­мые и со­от­вет­ствен­но в точ­ках и от­лич­ных от вер­шин тре­уголь­ни­ка. От­ре­зок ка­са­ет­ся окруж­но­сти, впи­сан­ной в тре­уголь­ник Най­ди­те длину от­рез­ка

За­да­ние 16 № 501069

Ре­ше­ние.

Обе точки и не могут ле­жать вне тре­уголь­ни­ка, по­сколь­ку в этом слу­чае от­ре­зок не может ка­сать­ся внев­пи­сан­ной окруж­но­сти. Зна­чит, по край­ней мере одна из этих точек лежит на сто­ро­не тре­уголь­ни­ке.

Пусть обе точки и лежат на сто­ро­нах тре­уголь­ни­ка (рис. 1).

Четырёхуголь­ник — впи­сан­ный, сле­до­ва­тель­но,

Зна­чит, тре­уголь­ник по­до­бен тре­уголь­ни­ку так как угол — общий. Пусть ко­эф­фи­ци­ент по­до­бия равен тогда

Суммы про­ти­во­по­лож­ных сто­рон опи­сан­но­го че­ты­рех­уголь­ни­ка равны:

Под­став­ляя из­вест­ные зна­че­ния сто­рон, на­хо­дим Сле­до­ва­тель­но,

Пусть точка лежит на про­дол­же­нии сто­ро­ны (рис. 2) Углы и равны, по­сколь­ку опи­ра­ют­ся на одну дугу. Зна­чит, тре­уголь­ник по­до­бен тре­уголь­ни­ку так как угол — общий. Более того, они опи­са­ны около одной и той же окруж­но­сти. Сле­до­ва­тель­но, ко­эф­фи­ци­ент по­до­бия равен 1, то есть тре­уголь­ни­ки и равны, по­это­му За­ме­тим, что и точка дей­стви­тель­но лежит на про­дол­же­нии сто­ро­ны

Если точка лежит на про­дол­же­нии сто­ро­ны то но ана­ло­гич­но преды­ду­ще­му слу­чаю по­лу­ча­ем Зна­чит, этот слу­чай не до­сти­га­ет­ся.

Ответ:

17. В банк был по­ло­жен вклад под бан­ков­ский про­цент 10%. Через год хо­зя­ин вкла­да снял со счета 2000 руб­лей, а еще через год снова внес 2000 руб­лей. Од­на­ко, вслед­ствие этих дей­ствий через три года со вре­ме­ни пер­во­на­чаль­но­го вло­же­ния вкла­да он по­лу­чил сумму мень­ше за­пла­ни­ро­ван­ной (если бы не было про­ме­жу­точ­ных опе­ра­ций со вкла­дом). На сколь­ко руб­лей мень­ше за­пла­ни­ро­ван­ной суммы по­лу­чил в итоге вклад­чик?

За­да­ние 17 № 508585

Ре­ше­ние.

Пусть вклад­чик в банк пер­во­на­чаль­но по­ло­жил х руб. Тогда за 3 года хра­не­ния этих денег вклад вырос бы до 1,331 х р, т. е. до р.

За пер­вый год хра­не­ния вкла­да он вырос до 1,1 р. Од­на­ко, через год вклад­чик снял 2000 р. На счету оста­лось р. В конце вто­ро­го года хра­не­ния вкла­да на эту сумму были на­чис­ле­ны про­цен­ты, вклад стал р. Од­на­ко, вклад­чик снова внес 2000 р. Сумма вкла­да стала р.

К концу тре­тье­го года хра­не­ния вкла­да ее сумма стала

 

 

И эту сумму снял вклад­чик в итоге вме­сто пер­во­на­чаль­но за­пла­ни­ро­ван­ной р.

Най­дем ис­ко­мую раз­ность.

 

 

Ответ: на 220 р.

18. При каких зна­че­ни­ях па­ра­мет­ра си­сте­ма имеет ре­ше­ния?

За­да­ние 18 № 511307

Ре­ше­ние.

Пе­ре­пи­шем ис­ход­ную си­сте­му в виде

 

Ис­ход­ная си­сте­ма имеет ре­ше­ния, тогда и толь­ко тогда, когда от­но­си­тель­но имеет ре­ше­ния си­сте­ма:

 

Решая пер­вое урав­не­ние этой си­сте­мы, на­хо­дим, что

Тре­бо­ва­ние за­да­чи будет вы­пол­не­но, если по­след­няя сме­шан­ная си­сте­ма имеет хотя бы одно ре­ше­ние. Ис­ко­мые зна­че­ния на­хо­дят­ся из со­во­куп­но­сти не­ра­венств

 

решая ко­то­рое, по­лу­ча­ем

Ответ: .

19. По­след­ние члены двух ко­неч­ных ариф­ме­ти­че­ских про­грес­сий a₁ = 5, a₂ = 8, ..., a_N и b₁ = 9, b₂ = 14, ..., b_M сов­па­да­ют, а сумма всех сов­па­да­ю­щих (взя­тых по од­но­му разу) чле­нов этих про­грес­сий равна 815. Най­ди­те число чле­нов в каж­дой про­грес­сии.

За­да­ние 19 № 507808

Ре­ше­ние.

Ясно, что

 

Общие члены про­грес­сий удо­вле­тво­ря­ют урав­не­нию:

 

 

Левая часть по­след­не­го урав­не­ния де­лит­ся на 3, по­это­му то есть или где Найдём Общие члены двух про­грес­сий сами об­ра­зу­ют ариф­ме­ти­че­скую про­грес­сию с пер­вым чле­ном рав­ным 14, а по­след­ним — рав­ным Зна­чит, от­ку­да По­это­му

 

Ответ: 49 и 29.

ВАРИАНТ№4

11. Поезд, дви­га­ясь рав­но­мер­но со ско­ро­стью 60 км/ч, про­ез­жа­ет мимо при­до­рож­но­го стол­ба за 9 се­кунд. Най­ди­те длину по­ез­да в мет­рах.

За­да­ние 11 № 116387

Ре­ше­ние.

Ско­рость по­ез­да равна

 м/с.

За 9 се­кунд поезд про­хо­дит мимо при­до­рож­но­го стол­ба рас­сто­я­ние рав­ное своей длине:

 

мет­ров.

Ответ: 150.

12. Най­ди­те точку мак­си­му­ма функ­ции .

За­да­ние 12 № 124817

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

Най­дем нули про­из­вод­ной:

 

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

 

Ис­ко­мая точка мак­си­му­ма .

 

Ответ: −10.

13. а) Ре­ши­те урав­не­ние

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку

За­да­ние 13 № 513365

Ре­ше­ние.

а) Имеем

 

 

от­ку­да

б) Корни, при­над­ле­жа­щие от­рез­ку отберём с по­мо­щью еди­нич­ной окруж­но­сти. По­лу­чим

Ответ: а) б)

14. В кубе ABCDA₁B₁C₁D₁ все реб­ра равны 1. Най­ди­те рас­сто­я­ние от точки C до пря­мой AD₁

За­да­ние 14 № 507651

Ре­ше­ние.

Про­ве­дем от­рез­ки CD₁ и AC. Ис­ко­мое рас­сто­я­ние равно длине пер­пен­ди­ку­ля­ра CH, про­ве­ден­но­го к пря­мой AD₁. Этот пер­пен­ди­ку­ляр яв­ля­ет­ся ме­ди­а­ной рав­но­сто­рон­не­го тре­уголь­ни­ка ACD₁ со сто­ро­ной

 

Ответ:

15. Ре­ши­те не­ра­вен­ство:

За­да­ние 15 № 511566

Ре­ше­ние.

Решим не­ра­вен­ство ме­то­дом ин­тер­ва­лов:

 

 

Ответ:

16. Точка M — се­ре­ди­на сто­ро­ны AD па­рал­ле­ло­грам­ма ABCD . Из вер­ши­ны A про­ве­де­ны два луча, ко­то­рые раз­би­ва­ют от­ре­зок BM на три рав­ные части.

а) До­ка­жи­те, что один из лучей со­дер­жит диа­го­наль па­рал­ле­ло­грам­ма.

б) Най­ди­те пло­щадь четырёхуголь­ни­ка, огра­ни­чен­но­го двумя про­ведёнными лу­ча­ми и пря­мы­ми BD и BC , если пло­щадь па­рал­ле­ло­грам­ма ABCD равна 120.

За­да­ние 16 № 511389

Ре­ше­ние.

а) Обо­зна­чим точки пе­ре­се­че­ния лучей с от­рез­ком BM — бук­ва­ми P и R (см. ри­су­нок), и пусть O — точка пе­ре­се­че­ния диа­го­на­лей па­рал­ле­ло­грам­ма, а N — точка пе­ре­се­че­ния луча AP и пря­мой BC.

Точка R делит ме­ди­а­ну BM тре­уголь­ни­ка ABD в от­но­ше­нии 2 :1 счи­тая от B. Сле­до­ва­тель­но, R лежит на ме­ди­а­не AO этого тре­уголь­ни­ка, то есть луч AR со­дер­жит диа­го­наль AC .

 

б) Пусть L — точка пе­ре­се­че­ния AN и BD. Нужно найти пло­щадь четырёхуголь­ни­ка LNCO. Пусть пло­щадь па­рал­ле­ло­грам­ма равна S . Пло­щадь тре­уголь­ни­ка BOC равна Найдём пло­щадь тре­уголь­ни­ка BNL . Из по­до­бия тре­уголь­ни­ков BPN и MPA сле­ду­ет, что

 

от­ку­да

 

Те­перь из по­до­бия тре­уголь­ни­ков BNL и DAL сле­ду­ет, что их со­от­вет­ству­ю­щие вы­со­ты от­но­сят­ся как 1:4 , а по­это­му вы­со­та тре­уголь­ни­ка BNL, про­ведённая к BN, со­став­ля­ет вы­со­ты па­рал­ле­ло­грам­ма, про­ведённой к сто­ро­не BC.

По­это­му

 

Сле­до­ва­тель­но, пло­щадь четырёхуголь­ни­ка LNCO равна

 

 

Ответ: 27.

17. В банк был по­ло­жен вклад под бан­ков­ский про­цент 10%. Через год хо­зя­ин вкла­да снял со счета 2000 руб­лей, а еще через год снова внес 2000 руб­лей. Од­на­ко, вслед­ствие этих дей­ствий через три года со вре­ме­ни пер­во­на­чаль­но­го вло­же­ния вкла­да он по­лу­чил сумму мень­ше за­пла­ни­ро­ван­ной (если бы не было про­ме­жу­точ­ных опе­ра­ций со вкла­дом). На сколь­ко руб­лей мень­ше за­пла­ни­ро­ван­ной суммы по­лу­чил в итоге вклад­чик?

Ре­ше­ние.

Пусть вклад­чик в банк пер­во­на­чаль­но по­ло­жил х руб. Тогда за 3 года хра­не­ния этих денег вклад вырос бы до 1,331 х р, т. е. до р.

За пер­вый год хра­не­ния вкла­да он вырос до 1,1 р. Од­на­ко, через год вклад­чик снял 2000 р. На счету оста­лось р. В конце вто­ро­го года хра­не­ния вкла­да на эту сумму были на­чис­ле­ны про­цен­ты, вклад стал р. Од­на­ко, вклад­чик снова внес 2000 р. Сумма вкла­да стала р.

К концу тре­тье­го года хра­не­ния вкла­да ее сумма стала

 

 

И эту сумму снял вклад­чик в итоге вме­сто пер­во­на­чаль­но за­пла­ни­ро­ван­ной р.

Най­дем ис­ко­мую раз­ность.

 

 

Ответ: на 220 р.

18. Най­ди­те все зна­че­ния a, при каж­дом из ко­то­рых урав­не­ние

 

 

имеет хотя бы один ко­рень.

Ре­ше­ние.

За­пи­шем ис­ход­ное урав­не­ние в виде

Пусть t = cosx, тогда ис­ход­ное урав­не­ние имеет хотя бы один ко­рень, если урав­не­ние имеет хотя бы один ко­рень, при­над­ле­жа­щий от­рез­ку [−1; 1]. Гра­фи­ком функ­ции яв­ля­ет­ся па­ра­бо­ла, ветви ко­то­рой на­прав­ле­ны вверх,

сле­до­ва­тель­но, урав­не­ние имеет хотя бы один ко­рень, при­над­ле­жа­щий от­рез­ку [−1; 1], либо при усло­вии (рис. 1) от­ку­да либо при усло­вии (рис. 2) от­ку­да

 Ответ:

19. Вин­ти­ки можно раз­ло­жить в па­ке­ти­ки, а па­ке­ти­ки упа­ко­вать в ко­роб­ки, по 3 па­ке­ти­ка в одну ко­роб­ку. Можно эти же вин­ти­ки раз­ло­жить в па­ке­ти­ки так, что в каж­дом па­ке­ти­ке будет на 3 вин­ти­ка боль­ше, чем рань­ше, но тогда в каж­дой ко­роб­ке будет ле­жать по 2 па­ке­ти­ка, а ко­ро­бок по­тре­бу­ет­ся на 2 боль­ше. Какое наи­боль­шее число вин­ти­ков может быть при таких усло­ви­ях?

Ре­ше­ние.

Пусть в каж­дой из ко­ро­бок лежит три па­ке­ти­ка, по вин­ти­ков в каж­дом. Во вто­ром слу­чае ко­ро­бок па­ке­ти­ков в ко­роб­ке 2, а вин­ти­ков в па­ке­ти­ке По усло­вию за­да­чи по­лу­ча­ем:

 

 

От­ку­да Учи­ты­вая, что числа и на­ту­раль­ные, по­лу­ча­ем, что — на­ту­раль­ный де­ли­тель числа 36. Ко­ли­че­ство вин­ти­ков при этом

 

 

Ре­ше­ние на­хо­дим пе­ре­бо­ром де­ли­те­лей.

 Ответ: 840.

При­ме­ча­ние.

Пе­ре­бор можно за­ме­нить ис­сле­до­ва­ни­ем функ­ции.

Функ­ция мо­но­тон­но убы­ва­ет при и мо­но­тон­но воз­рас­та­ет при Сле­до­ва­тель­но, наи­боль­шее зна­че­ние функ­ции до­сти­га­ет­ся, если — наи­боль­ший или наи­мень­ший на­ту­раль­ный де­ли­тель числа 36.

Если то

Если то

 

ВАРИАНТ№5

13. а) Ре­ши­те урав­не­ние

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку

За­да­ние 13 № 513365

Ре­ше­ние.

а) Имеем

 

 

от­ку­да

б) Корни, при­над­ле­жа­щие от­рез­ку отберём с по­мо­щью еди­нич­ной окруж­но­сти. По­лу­чим

Ответ: а) б)

14. В пря­мо­уголь­ном па­рал­ле­ле­пи­пе­де ABCDA₁B₁C₁D₁ из­вест­ны AB = 2, AD = AA₁ = 1. Най­ди­те угол между пря­мой AB₁ и плос­ко­стью ABC₁.

За­да­ние 14 № 500024

Ре­ше­ние.

Плос­ко­сти и пер­пен­ди­ку­ляр­ны. Пер­пен­ди­ку­ляр из точки к плос­ко­сти лежит в плос­ко­сти и пе­ре­се­ка­ет пря­мую в точке . Зна­чит, ис­ко­мый угол равен углу . В пря­мо­уголь­ном тре­уголь­ни­ке катет , ги­по­те­ну­за . По­это­му

 

.

 

Тогда .

 

Ответ: .

 

При­ме­ча­ние.

Воз­мож­ны дру­гие формы от­ве­та: .

 

15. Ре­ши­те не­ра­вен­ство .

За­да­ние 15 № 514448

Ре­ше­ние.

Пусть тогда имеем:

 

Вернёмся к ис­ход­ной пе­ре­мен­ной. Имеем:

 

 

Ответ:

16. В тре­уголь­ни­ке АВС про­ве­де­ны две вы­со­ты ВМ и CN, причём и .

а) До­ка­жи­те, что угол АВС тупой.

б) Най­ди­те от­но­ше­ние пло­ща­дей тре­уголь­ни­ков BMN и ABC.

За­да­ние 16 № 514047

Ре­ше­ние.

а) По­сколь­ку , точки C и M лежат по одну сто­ро­ну от точки А, а так как AM < CM, точка M лежит на от­рез­ке АС.

По­ло­жим АМ = 2x, CM = 3x. Из пря­мо­уголь­но­го тре­уголь­ни­ка ABM на­хо­дим, что

 

 

По тео­ре­ме Пи­фа­го­ра

 

 

По тео­ре­ме ко­си­ну­сов

 

 

Сле­до­ва­тель­но,

 

б) Из пря­мо­уголь­ных тре­уголь­ни­ков ANC и BNC на­хо­дим, что

 

 

зна­чит B — се­ре­ди­на AN.

Обо­зна­чим . Тогда

 

 

Сле­до­ва­тель­но,

 

 

 

Ответ:

17. По биз­нес-плану пред­по­ла­га­ет­ся вло­жить в четырёхлет­ний про­ект 10 млн руб­лей. По ито­гам каж­до­го года пла­ни­ру­ет­ся при­рост вло­жен­ных средств на 15% по срав­не­нию с на­ча­лом года. На­чис­лен­ные про­цен­ты оста­ют­ся вло­жен­ны­ми в про­ект. Кроме этого, сразу после на­чис­ле­ний про­цен­тов нужны до­пол­ни­тель­ные вло­же­ния: целое число n млн руб­лей в пер­вый и вто­рой годы, а также целое число m млн руб­лей в тре­тий и четвёртый годы.

Най­ди­те наи­мень­шие зна­че­ния n и m, при ко­то­рых пер­во­на­чаль­ные вло­же­ния за два года как ми­ни­мум удво­ят­ся, а за че­ты­ре года как ми­ни­мум утро­ят­ся.

За­да­ние 17 № 513431

Ре­ше­ние.

К на­ча­лу 2-го года по­лу­чит­ся млн вло­же­ний, а к на­ча­лу 3-го года —

 

 

По усло­вию Наи­мень­шее целое ре­ше­ние n = 4. Тогда к на­ча­лу 3-го года по­лу­чит­ся

 

млн.

 

К на­ча­лу 4-года имеем млн, а в конце про­ек­та

 

 

По усло­вию По­лу­ча­ем, что m = 1 — наи­мень­шее целое ре­ше­ние.

 

Ответ: 4 и 1 млн руб.

18. Най­ди­те все зна­че­ния па­ра­мет­ра при каж­дом из ко­то­рых си­сте­ма урав­не­ний имеет ровно че­ты­ре ре­ше­ния.

За­да­ние 18 № 484641

Ре­ше­ние.

Пре­об­ра­зу­ем дан­ную си­сте­му:

 

Сде­лав за­ме­ну пе­ре­мен­ной , по­лу­ча­ем си­сте­му

 

За­ме­тим, что ко­ли­че­ство ре­ше­ний по­лу­чен­ной си­сте­мы сов­па­да­ет с ко­ли­че­ством ре­ше­ний ис­ход­ной си­сте­мы. По­стро­им гра­фи­ки урав­не­ний (1) и (2) в си­сте­ме ко­ор­ди­нат

 

Гра­фик пер­во­го урав­не­ния — ромб, диа­го­на­ли ко­то­ро­го, рав­ные 8 и 6, лежат со­от­вет­ствен­но на осях и а гра­фи­ком вто­ро­го урав­не­ния яв­ля­ет­ся окруж­ность с цен­тром в на­ча­ле ко­ор­ди­нат и ра­ди­у­сом (см. ри­су­нок).

 

Гра­фи­ки урав­не­ний си­сте­мы имеют ровно че­ты­ре общих точки, и, сле­до­ва­тель­но, си­сте­ма имеет ровно че­ты­ре ре­ше­ния, тогда и толь­ко тогда, когда окруж­ность либо впи­са­на в ромб, либо ее ра­ди­ус удо­вле­тво­ря­ет усло­вию

 

.

В пер­вом слу­чае ра­ди­ус окруж­но­сти яв­ля­ет­ся вы­со­той пря­мо­уголь­но­го тре­уголь­ни­ка с ка­те­та­ми, рав­ны­ми 3 и 4, от­ку­да

 

, .

Во вто­ром слу­чае по­лу­ча­ем , от­ку­да

 

или .

Ответ:

19. Най­ди­те все пары на­ту­раль­ных чисел m и n, яв­ля­ю­щи­е­ся ре­ше­ни­я­ми урав­не­ния 3ⁿ − 2^m = 1.

Ре­ше­ние.

Пусть — чет­ное число Тогда Пра­вая часть — про­из­ве­де­ние двух по­сле­до­ва­тель­ных чет­ных чисел, каж­дое из ко­то­рых яв­ля­ет­ся сте­пе­нью числа 2. Зна­чит, и от­ку­да и При этом сле­до­ва­тель­но,

Пусть те­перь —не­чет­ное число. Все не­чет­ные сте­пе­ни трой­ки де­лят­ся на 4 с остат­ком 3. Зна­чит, де­лит­ся на 4 с остат­ком 2. Из ра­вен­ства по­лу­ча­ем, что в этом слу­чае (если то де­лит­ся на 4 без остат­ка). При этом от­ку­да

 

Ответ: или

 

ВАРИАНТ№6

13. а) Ре­ши­те урав­не­ние

б) Най­ди­те все корни этого урав­не­ния, при­над­ле­жа­щие от­рез­ку

Ре­ше­ние.

а) За­пи­шем урав­не­ние в виде

 

Зна­чит, или  — урав­не­ние не имеет кор­ней, или , от­ку­да , .

б) С по­мо­щью чис­ло­вой окруж­но­сти от­бе­рем корни урав­не­ния, при­над­ле­жа­щие от­рез­ку

По­лу­чим число

Ответ: а) б)

14. В пра­виль­ной тре­уголь­ной приз­ме ABCA₁B₁C₁ сто­ро­ны ос­но­ва­ния равны 4, бо­ко­вые рёбра равны 7, точка D — се­ре­ди­на ребра BB₁.

а) Пусть пря­мые C₁D и BC пе­ре­се­ка­ют­ся в точке E. До­ка­жи­те, что угол EAC — пря­мой.

б) Най­ди­те угол между плос­ко­стя­ми ABC и ADC₁.

Ре­ше­ние.

а) В тре­уголь­ни­ке от­ре­зок BD — сред­няя линия (так как па­рал­ле­лен и равен его по­ло­ви­не), зна­чит EB = BC = AB и тре­уголь­ник — рав­но­бед­рен­ный. Тогда

 

И      

б) По­сколь­ку и (так как ), имеем По­сколь­ку плос­ко­сти ABC и пе­ре­се­ка­ют­ся по пря­мой AE, имеем

 

Ответ:

15. Ре­ши­те не­ра­вен­ство:

Ре­ше­ние.

Сде­ла­ем за­ме­ну

 

 Воз­вра­ща­ясь к ис­ход­ной пе­ре­мен­ной, по­лу­чим: или  

Ответ:

16. В окруж­но­сти про­ве­де­ны хорды PQ и CD, причём PQ = PD = CD = 8, CQ = 6. Най­ди­те CP.

Ре­ше­ние.

Воз­мож­ны два слу­чая.

Пер­вый слу­чай: хорды PQ и CD не пе­ре­се­ка­ют­ся (рис. 1), тогда ∠PQC = 180° − ∠PDC.

 

В тре­уголь­ни­ках PQC и PDC 

Зна­чит, от­ку­да

Вто­рой слу­чай: хорды PQ и CD пе­ре­се­ка­ют­ся (рис. 2), тогда

В тре­уголь­ни­ках PQC и PDC  

от­ку­да

 Ответ: 4 или

17. В ян­ва­ре 2000 года став­ка по де­по­зи­там в банке «Воз­рож­де­ние» со­ста­ви­ла х % го­до­вых, тогда как в ян­ва­ре 2001 года — у% го­до­вых, при­чем из­вест­но, что x + y = 30%. В ян­ва­ре 2000 года вклад­чик от­крыл счет в банке «Воз­рож­де­ние», по­ло­жив на него не­ко­то­рую сумму. В ян­ва­ре 2001 года, по про­ше­ствии года с того мо­мен­та, вклад­чик снял со счета пятую часть этой суммы. Ука­жи­те зна­че­ние х при ко­то­ром сумма на счету вклад­чи­ка в ян­ва­ре 2002 года ста­нет мак­си­маль­но воз­мож­ной.

Ре­ше­ние.

Пусть в ян­ва­ре 2000 года вклад­чик по­ло­жил на счет у. е. Тогда в ян­ва­ре 2001 года на счету сумма ста­нет у. е. Но в ян­ва­ре же 2001 года вклад­чик снял у. е. На счету оста­лось:

 у. е.

В ян­ва­ре 2002 года сумма на счету будет равна:

 

Функ­ция яв­ля­ет­ся квад­ра­тич­ной от .

 У нее есть наи­боль­шее зна­че­ние при

 Ответ: 25.

18. Най­ди­те все зна­че­ния a, при ко­то­рых любое ре­ше­ние урав­не­ния

 

при­над­ле­жит от­рез­ку

Ре­ше­ние.

Рас­смот­рим функ­цию Она опре­де­ле­на при воз­рас­та­ет на об­ла­сти опре­де­ле­ния и при­ни­ма­ет все зна­че­ния от до Зна­чит, урав­не­ние имеет един­ствен­ное ре­ше­ние. Это ре­ше­ние при­над­ле­жит от­рез­ку тогда и толь­ко тогда, когда и По­лу­ча­ем си­сте­му не­ра­венств:

 

 

Ответ:

19. Най­ди­те все про­стые числа b, для каж­до­го из ко­то­рых су­ще­ству­ет такое целое число а, что дробь можно со­кра­тить на b.

Ре­ше­ние.

Если целые числа и де­лят­ся на b, то целое число

 

также де­лит­ся на b. Тогда число  

тоже де­лит­ся на b.

 Тогда число     также де­лит­ся на b.

 Таким об­ра­зом, ис­ко­мое b — про­стой де­ли­тель числа 56, то есть 2 или 7. Оста­лось про­ве­рить, для каких из най­ден­ных чисел можно по­до­брать а. Если а не­чет­ное, то чис­ли­тель и зна­ме­на­тель дан­ной дроби — чет­ные числа, по­это­му дробь можно со­кра­тить на 2. Если а крат­но 7, то чис­ли­тель и зна­ме­на­тель дан­ной дроби также крат­ны 7, по­это­му дробь можно со­кра­тить на 7.

 

Ответ: 2, 7.

 

ВАРИАНТ№7

11.

Цена хо­ло­диль­ни­ка в ма­га­зи­не еже­год­но умень­ша­ет­ся на одно и то же число про­цен­тов от преды­ду­щей цены. Опре­де­ли­те, на сколь­ко про­цен­тов каж­дый год умень­ша­лась цена хо­ло­диль­ни­ка, если, вы­став­лен­ный на про­да­жу за 20 900 руб­лей, через два года был про­дан за 16 929 руб­лей.

За­да­ние 11 № 107949

Ре­ше­ние.

Пусть цена хо­ло­диль­ни­ка еже­год­но сни­жа­лась на про­цен­тов в год. Тогда за два года она сни­зи­лась на , от­ку­да имеем:

Ответ: 10.

12.

Най­ди­те наи­мень­шее зна­че­ние функ­ции на от­рез­ке .

За­да­ние 12 № 130803

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

 

 

 

Най­дем нули про­из­вод­ной:

 

 

 

Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

 

В точке за­дан­ная функ­ция имеет ми­ни­мум, яв­ля­ю­щий­ся ее наи­мень­шим зна­че­ни­ем на за­дан­ном от­рез­ке. Най­дем это наи­мень­шее зна­че­ние:

.

 

Ответ: 0.

13. Ре­ши­те урав­не­ние

За­да­ние 13 № 507668

Ре­ше­ние.

Левая часть урав­не­ния имеет смысл при и Вы­ра­же­ние по­ло­жи­тель­но при всех до­пу­сти­мых Зна­чит,

 

 

 

Учи­ты­вая, что и по­лу­ча­ем, что ре­ше­ни­я­ми яв­ля­ют­ся числа

 

Ответ:

14. Дан куб ABCDA₁B₁C₁D₁. Длина ребра куба равна 1. Най­ди­те рас­сто­я­ние от се­ре­ди­ны от­рез­ка BC₁ до плос­ко­сти AB₁D₁.

За­да­ние 14 № 484571

Ре­ше­ние.

Пусть  — се­ре­ди­на  — се­ре­ди­на зна­чит, Кроме того, сле­до­ва­тель­но, плос­кость Опу­стим пер­пен­ди­ку­ляр из точки на пря­мую кроме этого, (так как лежит в плос­ко­сти ), сле­до­ва­тель­но, и яв­ля­ет­ся ис­ко­мым рас­сто­я­ни­ем.

Ис­ко­мый от­ре­зок яв­ля­ет­ся вы­со­той пря­мо­уголь­но­го тре­уголь­ни­ка с пря­мым углом

По­это­му

 

 

Ответ:

15. Ре­ши­те не­ра­вен­ство:

За­да­ние 15 № 508442

Ре­ше­ние.

По тео­ре­ме, об­рат­ной тео­ре­ме Виета, сумма кор­ней урав­не­ния равна , а их про­из­ве­де­ние равно . По­это­му корни этого урав­не­ния — числа и . Тогда не­ра­вен­ство можно ре­шить так:

 

Ответ:

16. В тре­уголь­ни­ке из­вест­ны сто­ро­ны: . Окруж­ность, про­хо­дя­щая через точки и , пе­ре­се­ка­ет пря­мые и со­от­вет­ствен­но в точ­ках и , от­лич­ных от вер­шин тре­уголь­ни­ка. От­ре­зок ка­са­ет­ся окруж­но­сти, впи­сан­ной в тре­уголь­ник . Най­ди­те длину от­рез­ка .

За­да­ние 16 № 511338

Ре­ше­ние.

Обе точки и не могут ле­жать вне тре­уголь­ни­ка, по­сколь­ку в этом слу­чае от­ре­зок не может ка­сать­ся впи­сан­ной окруж­но­сти. Зна­чит, по край­ней мере одна из этих точек лежит на сто­ро­не тре­уголь­ни­ка.

Пусть обе точки и лежат на сто­ро­нах тре­уголь­ни­ка. Че­ты­рех­уголь­ник  — впи­сан­ный, сле­до­ва­тель­но,

 

 

Зна­чит, тре­уголь­ник по­до­бен тре­уголь­ни­ку , так как угол  — общий. Пусть ко­эф­фи­ци­ент по­до­бия равен , тогда , , . Суммы про­ти­во­по­лож­ных сто­рон опи­сан­но­го че­ты­рех­уголь­ни­ка равны:

 

 

Под­став­ляя из­вест­ные зна­че­ния сто­рон, на­хо­дим . Сле­до­ва­тель­но, .

Пусть точка лежит на про­дол­же­нии сто­ро­ны . Углы и равны, по­сколь­ку опи­ра­ют­ся на одну дугу. Зна­чит, тре­уголь­ник по­до­бен тре­уголь­ни­ку , так как угол  — общий. Более того, они опи­са­ны около одной и той же окруж­но­сти. Сле­до­ва­тель­но, ко­эф­фи­ци­ент по­до­бия равен 1, то есть, тре­уголь­ни­ки и равны, по­это­му . За­ме­тим, что и точка дей­стви­тель­но лежит на про­дол­же­нии сто­ро­ны .

Если точка лежит на про­дол­же­нии сто­ро­ны , то , но, ана­ло­гич­но преды­ду­ще­му слу­чаю, по­лу­ча­ем . Зна­чит, этот слу­чай не до­сти­га­ет­ся.

 

Ответ: .

17. В июле 2016 года пла­ни­ру­ет­ся взять кре­дит в банке в раз­ме­ре S тыс. руб­лей, где S — на­ту­раль­ное число, на 3 года. Усло­вия его воз­вра­та та­ко­вы

− каж­дый ян­варь долг уве­ли­чи­ва­ет­ся на 15% по срав­не­нию с кон­цом преды­ду­ще­го года;

− с фев­ра­ля по июнь каж­до­го года не­об­хо­ди­мо вы­пла­тить одним пла­те­жом часть долга;

− в июле каж­до­го года долг дол­жен со­став­лять часть кре­ди­та в со­от­вет­ствии со сле­ду­ю­щей таб­ли­цей.

 

Месяц и год	Июль 2016	Июль 2017	Июль 2018	Июль 2019
Долг (в тыс. руб­лей)	S	0,7S	0,4S	0

 

Най­ди­те наи­мень­шее зна­че­ние S, при ко­то­ром каж­дая из вы­плат будет со­став­лять целое число тысяч руб­лей.

За­да­ние 17 № 514627

Ре­ше­ние.

Долг перед бан­ком (в тыс. руб­лей) по со­сто­я­нию на июль каж­до­го года дол­жен умень­шить­ся до нуля сле­ду­ю­щим об­ра­зом:

 

 

По усло­вию, в ян­ва­ре каж­до­го года долг уве­ли­чи­ва­ет­ся на 15% зна­чит, долг в ян­ва­ре каж­до­го года равен:

 

 

Сле­до­ва­тель­но, вы­пла­ты с фев­ра­ля по июнь каж­до­го года со­став­ля­ют:

 

 

По усло­вию, числа

 

 

долж­ны быть це­лы­ми. Зна­чит, число S долж­но де­лить­ся на 20, 200 и 50. Наи­мень­шее общее крат­ное этих чисел равно 200.

 

Ответ: 200.

18. Най­ди­те все зна­че­ния па­ра­мет­ра a, при ко­то­рых урав­не­ние имеет един­ствен­ное ре­ше­ние.

За­да­ние 18 № 501419

Ре­ше­ние.

 

 

Не­ра­вен­ство за­да­ет на ко­ор­ди­нат­ной плос­ко­сти «верх­нюю» по­лу­плос­кость с гра­ни­цей а урав­не­ние при  ― окруж­ность с цен­тром и ра­ди­у­сом (см. ри­су­нок).

 

Окруж­ность и по­лу­плос­кость имеют ровно одну общую точку тогда и толь­ко тогда, когда ра­ди­ус окруж­но­сти равен по­ло­ви­не диа­го­на­ли PO квад­ра­та APBO, т. е., от­ку­да

При урав­не­ние, а, сле­до­ва­тель­но, и вся си­сте­ма ре­ше­ний не имеют, а при ре­ше­ни­ем урав­не­ния яв­ля­ет­ся пара ко­то­рая не удо­вле­тво­ря­ет не­ра­вен­ству

Ответ:

19. Мно­же­ство чисел назовём хо­ро­шим, если его можно раз­бить на два под­мно­же­ства с оди­на­ко­вой сум­мой чисел.

а) Яв­ля­ет­ся ли мно­же­ство {200; 201; 202; ...; 299} хо­ро­шим?

б) Яв­ля­ет­ся ли мно­же­ство {2; 4; 8; ...; 2¹⁰⁰} хо­ро­шим?

в) Сколь­ко хо­ро­ших четырёхэле­мент­ных под­мно­жеств у мно­же­ства {1; 2; 4; 5; 7; 9; 11}?

Ре­ше­ние.

а) Разобьём мно­же­ство {200, 201, 202, ..., 299} на два мно­же­ства пя­ти­де­ся­ти­эле­мент­ных мно­же­ства сле­ду­ю­щим об­ра­зом: 

{200, 299, 202, 297, 204, 295, ..., 248, 251},

{201; 298; 203; 296; 205, 294, ..., 249, 250}.

 

Сумма чисел в этих двух под­мно­же­ствах оди­на­ко­ва, по­это­му ис­ход­ное множе­ство яв­ля­ет­ся хо­ро­шим. (Воз­мож­ны и дру­гие при­ме­ры.)

 б) За­ме­тим, сумма чисел в под­мно­же­стве, ко­то­рое будет со­дер­жать число будет боль­ше суммы чисел в дру­гом под­мно­же­стве, по­сколь­ку боль­ше суммы всех осталь­ных чисел:

 

Сле­до­ва­тель­но, мно­же­ство {2; 4; 8; ...; 2¹⁰⁰} не яв­ля­ет­ся хо­ро­шим.

 в) За­ме­тим, что четырёхэле­мент­ное мно­же­ство яв­ля­ет­ся хо­ро­шим в двух слу­ча­ях: либо одно число яв­ля­ет­ся сум­мой трёх дру­гих, либо мно­же­ство со­дер­жит две пары чисел с рав­ны­ми сум­ма­ми.

Под­мно­же­ства мно­же­ства {1; 2; 4; 5; 7; 9; 11}, удо­вле­тво­ря­ю­щие пер­во­му слу­чаю, — это {1; 2; 4; 7} и {2; 4; 5; 11}.

Рас­смот­рим вто­рой слу­чай и за­ме­тим, что если мно­же­ство со­дер­жит две пары чисел с рав­ны­ми сум­ма­ми, то сумма всех чисел чётна. Сле­до­ва­тель­но, чет­ные числа 2 и 4 либо од­но­вре­мен­но вхо­дят в хо­ро­шее четырёхэле­мент­ное под­мно­же­ство, либо од­но­вре­мен­но не вхо­дят в него.

Если 2 и 4 вхо­дят в под­мно­же­ство, то либо сумма двух дру­гих чисел равна 6, это под­мно­же­ство {1; 2; 4; 5}, либо раз­ность двух дру­гих чисел равна 2, это под­мно­же­ства:

 {1; 2; 4; 5}; {2; 4; 5; 7}; {2; 4; 7; 9}; {2; 4; 9; 11}.

Если 2 и 4 не вхо­дят в под­мно­же­ство, то хо­ро­шее под­мно­же­ство лежит во мно­же­стве {1; 5; 7; 9; 11}. По­лу­ча­ем хо­ро­шие под­мно­же­ства:

 {1; 5; 7; 11} и {5; 7; 9; 11}.

Всего най­де­но 8 хо­ро­ших под­мно­жеств. Дру­гих ва­ри­ан­тов нет.

 Ответ: а) да; б) нет; в) 8.

ВАРИНТ№8

11. Пер­вые 120 км ав­то­мо­биль ехал со ско­ро­стью 90 км/ч, сле­ду­ю­щие 100 км — со ско­ро­стью 100 км/ч, а затем 110 км — со ско­ро­стью 110 км/ч. Най­ди­те сред­нюю ско­рость ав­то­мо­би­ля на про­тя­же­нии всего пути. Ответ дайте в км/ч.

Ре­ше­ние.

Чтобы найти сред­нюю ско­рость на про­тя­же­нии пути, нужно весь путь раз­де­лить на все время дви­же­ния. Прой­ден­ный путь равен 120 + 100 + 110  =  330 км. Сред­няя ско­рость ав­то­мо­би­ля равна

 

км/ч.

Ответ: 99.

12. Най­ди­те наи­мень­шее зна­че­ние функ­ции на от­рез­ке

Ре­ше­ние.

Най­дем про­из­вод­ную за­дан­ной функ­ции:

Най­дем нули про­из­вод­ной:

 Опре­де­лим знаки про­из­вод­ной функ­ции и изоб­ра­зим на ри­сун­ке по­ве­де­ние функ­ции:

 

 Най­ден­ная про­из­вод­ная не­от­ри­ца­тель­на на за­дан­ном от­рез­ке, за­дан­ная функ­ция воз­рас­та­ет на нем, по­это­му наи­мень­шим зна­че­ни­ем функ­ции на от­рез­ке яв­ля­ет­ся:

 

 Ответ: −13.

13. а) Ре­ши­те урав­не­ние .

б) Ука­жи­те корни этого урав­не­ния, при­над­ле­жа­щие про­ме­жут­ку .

Ре­ше­ние.

а) Пре­об­ра­зу­ем урав­не­ние:

 

 

 б) Най­дем корни, ле­жа­щие на за­дан­ном от­рез­ке. Со­ста­вим двой­ное не­ра­вен­ство:

 

,

от­ку­да

.

Сле­до­ва­тель­но, или , тогда ис­ко­мые корни и

 Ответ: а) б) и

14. В пра­виль­ной четырёхуголь­ной приз­ме ABCDA₁B₁C₁D₁ сто­ро­на ос­но­ва­ния AB=6, а бо­ко­вое ребро На рёбрах AB, A₁D₁ и C₁D₁ от­ме­че­ны точки M, N и K со­от­вет­ствен­но, причём AM = A₁N = C₁K = 1.

а) Пусть L — точка пе­ре­се­че­ния плос­ко­сти MNK с реб­ром BC. До­ка­жи­те, что MNKL — квад­рат.

б) Най­ди­те пло­щадь се­че­ния приз­мы плос­ко­стью MNK.

Ре­ше­ние.

а) Плос­кость MNK пе­ре­се­ка­ет плос­ко­сти ос­но­ва­ний ABCD и A₁B₁C₁D₁ по па­рал­лель­ным пря­мым, сле­до­ва­тель­но, пря­мые NK и ML па­рал­лель­ны, а CL = 1.

По­ка­жем, что сто­ро­ны четырёхуголь­ни­ка MNKL равны и диа­го­на­ли равны:

По­это­му MNKL — квад­рат.

б) Пусть W — точка пе­ре­се­че­ния пря­мых NK и A₁B₁. Тогда, так как , по­лу­ча­ем по­это­му пря­мая WM, а зна­чит и плос­кость MWK пе­ре­се­ка­ет ребро AA₁ в его се­ре­ди­не E. Ана­ло­гич­но, плос­кость MNK пе­ре­се­ка­ет ребро CC₁ в его се­ре­ди­не F.

В пря­мо­уголь­ни­ке AEFC про­ти­во­по­лож­ные сто­ро­ны: Се­че­ние MENKFL со­сто­ит из двух рав­ных тра­пе­ций ENKF и EMLF, причём пря­мая MN пер­пен­ди­ку­ляр­на их ос­но­ва­ни­ям. По­это­му ис­ко­мая пло­щадь се­че­ния равна

 

Ответ: а) до­ка­за­но; б) 55.

15. Ре­ши­те не­ра­вен­ство:

Ре­ше­ние.

Решим не­ра­вен­ство ме­то­дом ин­тер­ва­лов:

Ответ:

16. Окруж­ность ра­ди­у­са впи­са­на в пря­мой угол. Вто­рая окруж­ность также впи­са­на в этот угол и пе­ре­се­ка­ет­ся с пер­вой в точ­ках M и N. Из­вест­но, что рас­сто­я­ние между цен­тра­ми окруж­но­стей равно 6. Най­ди­те MN.

Ре­ше­ние.

Пусть O₁ — центр окруж­но­сти ра­ди­у­са O₂ — центр вто­рой окруж­но­сти, A — вер­ши­на пря­мо­го угла, тогда

Воз­мож­ны два слу­чая. Пер­вый слу­чай: точка O₁ лежит между точ­ка­ми A и O₂ (рис. 1), тогда O₂A = O₁A + O₁O₂ = 14, от­ку­да ра­ди­ус вто­рой окруж­но­сти

 В тре­уголь­ни­ке O₁MO₂ имеем O₁O₂ = 6, По­сколь­ку общая хорда MN окруж­но­стей пер­пен­ди­ку­ляр­на линии цен­тров O₁O₂ и де­лит­ся ею по­по­лам, вы­со­та MH тре­уголь­ни­ка O₁MO₂ равна по­ло­ви­не MN.

 В тре­уголь­ни­ке O₁MO₂ по­лу­пе­ри­метр

 

от­ку­да

 Вто­рой слу­чай: точка O₂ лежит между точ­ка­ми A и O₁ (рис. 2), тогда O₂A = O₁A − O₁O₂ от­ку­да ра­ди­ус вто­рой окруж­но­сти

В тре­уголь­ни­ке O₁MO₂ имеем O₁O₂ = 12, Ана­ло­гич­но пер­во­му слу­чаю, вы­со­та MH тре­уголь­ни­ка O₁MO₂ равна по­ло­ви­не MN.

В тре­уголь­ни­ке O₁MO₂ по­лу­пе­ри­метр

 

от­ку­да

 Ответ: или

17. В июле 2016 года пла­ни­ру­ет­ся взять кре­дит в банке на пять лет в раз­ме­ре S тыс руб­лей. Усло­вия его воз­вра­та та­ко­вы:

− каж­дый ян­варь долг воз­рас­та­ет на 20% по срав­не­нию с кон­цом преды­ду­ще­го года;

− с фев­ра­ля по июнь каж­до­го года не­об­хо­ди­мо вы­пла­тить часть долга;

− в июле 2017,2018 и 2019 долг остаётся рав­ным S тыс. руб­лей;

− вы­пла­ты в 2020 и 2021 годах равны по 360 тыс. руб­лей;

− к июлю 2021 долг будет вы­пла­чен пол­но­стью.

Най­ди­те общую сумму вы­плат за пять лет.

Ре­ше­ние.

В июле 2017, 2018 и 2019 годов долг перед бан­ком не ме­ня­ет­ся, а еже­год­ные вы­пла­ты со­став­ля­ют 0,2S тыс. руб­лей.

В ян­ва­ре 2020 года долг (в тыс. руб­лей) равен 1,2S, а в июле — 1,2S − 360.

В ян­ва­ре 2021 года долг равен 1,44S − 432, а в июле 1,44S − 792.

По усло­вию, долг будет вы­пла­чен пол­но­стью, зна­чит, 1,44S — 792 = 0, от­ку­да S = 550.

Таким об­ра­зом, пер­вые три вы­пла­ты со­став­ля­ют по 110 тыс. руб­лей, а по­след­ние две — по 360 тыс. руб­лей.

Общая сумма вы­плат со­став­ля­ет:

 

 Ответ: 1050 тыс. руб­лей.

18. Най­ди­те все зна­че­ния па­ра­мет­ра при каж­дом из ко­то­рых си­сте­ма

 

имеет ровно ре­ше­ний.

Ре­ше­ние.

Пре­об­ра­зу­ем си­сте­му, по­лу­чим:

 

Пер­вое урав­не­ние за­да­ет части двух па­ра­бол (см. ри­су­нок): 

 

Вто­рое урав­не­ние за­да­ет окруж­ность ра­ди­у­сом с цен­тром На ри­сун­ке видно, что шесть ре­ше­ний си­сте­мы по­лу­ча­ют­ся, толь­ко если окруж­ность про­хо­дит через точки и пе­ре­се­кая па­ра­бо­лу еще в че­ты­рех точ­ках.

При этом ра­ди­ус окруж­но­сти равен от­ку­да или

 

Ответ:

19. Най­ди­те все трой­ки на­ту­раль­ных чисел k, m и n, удо­вле­тво­ря­ю­щие урав­не­нию

Ре­ше­ние.

1. Так как то и

2. Пусть тогда от­ку­да и

3. Пусть тогда от­ку­да и

4. Далее ко­неч­ным пе­ре­бо­ром зна­че­ний на­хо­дим все ре­ше­ния:

Можно за­ме­тить, что это урав­не­ние сим­мет­рич­но отн. зна­че­ний n и k и мы можем пе­ре­брать мень­ше ва­ри­ан­тов.

 

 

 

 

 

 

Ответ:

 

Скачано с www.znanio.ru