Домашнее задание по вероятности и статистике 8 класс "Дерево случайного опыта"

Дерево случайного опыта.

Важно! При построении дерева нужно следить, чтобы сумма вероятностей около всех рёбер, выходящих из одной вершины, была равна единице.

Элементарные события эксперимента в дереве изображаются концевыми вершинами дерева. К каждой концевой вершине ведёт единственная цепочка от точки S. Поэтому можно считать, что элементарные события изображаются не только концевыми вершинами, но и соответствующими цепочками.

1. На рисунке 1 изображено дерево некоторого случайного опыта с началом в точке S. Сколько элементарных событий в этом опыте?

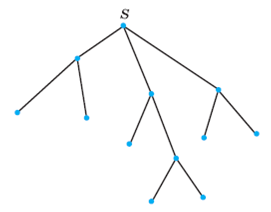
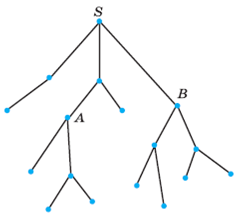
Рис. 1                                                                                Рис. 2

2. На рисунке 2 изображено дерево некоторого случайного опыта с началом в точке S. События А и В изображены промежуточными вершинами дерева. Сколько элементарных событий этого опыта благоприятствуют:

а) событию А; б) событию В?

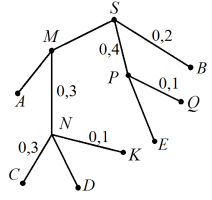
3. На рисунке изображено дерево некоторого случайного эксперимента с началом в точке . S

а) Изобразите дерево в своей тетради и напишите недостающие вероятности на рёбрах.

б) Сколько в этом случайном эксперименте элементарных событий?

в) Найдите вероятность цепочки . SMNK

г) Найдите вероятность события . E

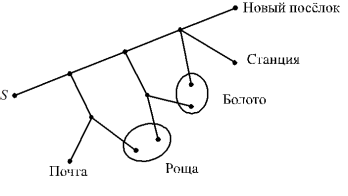4. Алексей выходит из точки и движется по дорожкам, которые показаны на рисунке 17. На каждой развилке Алексей равновероятно выбирает дальнейший путь, но не возвращается обратно. Найдите вероятность того, что таким образом он попадёт: S

а) в Новый посёлок;

б) в болото;

в) на почту или на станцию.