Доп материал для проверки знаний по геометрии в ОГЭ

15. В прямоугольном треугольнике ABC катет AC = 80, а высота CH, опущенная на гипотенузу, равна  Найдите 

16. Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 17. Найдите AC, если 

17. 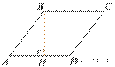Высота BH ромба ABCD делит его сторону AD на отрезки  и  Найдите площадь ромба.

18. На клетчатой бумаге с размером клетки 1х1 изображена фигура. Найдите её площадь.

19. Какие из следующих утверждений верны?

1)  Если две стороны треугольника равны 4 и 5, а угол между ними равен 30°, то площадь этого треугольника равна 10.

2)  Площадь трапеции равна произведению суммы оснований на высоту.

3)  Площадь трапеции не превосходит произведения средней линии на высоту.

4)  Площадь треугольника равна половине произведения его стороны на высоту, проведенную к этой стороне.

15. Радиус окружности с центром в точке O равен 29, длина хорды AB равна 40 (см. рис.). Найдите расстояние от хорды AB до параллельной ей касательной k.

16. Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите  если  Ответ дайте в градусах.

17. 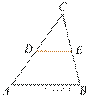В треугольнике ABC известно, что DE  — средняя линия. Площадь треугольника CDE равна 67. Найдите площадь треугольника ABC.

18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до середины отрезка ВС. Ответ выразите в сантиметрах.

19. Какие из следующих утверждений верны?

1)  Квадрат любой стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на синус угла между ними.

2)  Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна 13.

3)  Треугольник ABC, у которого AB = 5, BC = 6, AC = 7, является остроугольным.

4)  В прямоугольном треугольнике квадрат катета равен разности квадратов гипотенузы и другого катета.

15. В выпуклом четырехугольнике ABCD известно, что     Найдите угол A. Ответ дайте в градусах.

16. 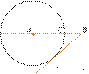На отрезке AB выбрана точка C так, что  и  Построена окружность с центром A, проходящая через C. Найдите длину отрезка касательной, проведённой из точки B к этой окружности.

17. 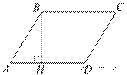Высота BH ромба ABCD делит его сторону AD на отрезки  и  Найдите площадь ромба.

18. 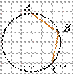Найдите угол ABC. Ответ дайте в градусах.

19. Какое из следующих утверждений верно?

1)  Все равнобедренные треугольники подобны.

2)  Существует прямоугольник, диагонали которого взаимно перпендикулярны.

3)  Сумма углов прямоугольного треугольника равна 90 градусам.

15. В треугольнике два угла равны 27° и 79°. Найдите его третий угол. Ответ дайте в градусах.

16. 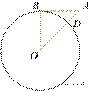Отрезок AB  =  63 касается окружности радиуса 60 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.

17. 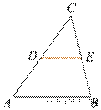В треугольнике ABC известно, что DE  — средняя линия. Площадь треугольника CDE равна 21. Найдите площадь треугольника ABC.

18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки A, B и C. Найдите расстояние от точки A до середины отрезка BC. Ответ выразите в сантиметрах.

19. Какие из данных утверждений верны? Запишите их номера.

1)  Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.

2)  Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник  — ромб.

3)  Площадь круга меньше квадрата длины его диаметра.

15. 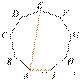##ABCDEFGHI  — правильный девятиугольник. Найдите угол EAI. Ответ дайте в градусах.

16. Сторона AC треугольника ABC проходит через центр описанной около него окружности. Найдите  если  Ответ дайте в градусах.

17. 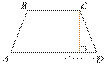Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 17. Найдите длину основания BC.

18. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

19. Какие из данных утверждений верны? Запишите их номера.

1)  Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.

2)  В любой четырёхугольник можно вписать окружность.

3)  Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.

15. Точка O  — центр окружности, на которой лежат точки A, B и C таким образом, что OABC  — ромб. Найдите угол OCB. Ответ дайте в градусах.

16. 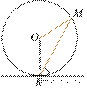Прямая касается окружности в точке K. Точка O  — центр окружности. Хорда KM образует с касательной угол, равный 75°. Найдите величину угла OMK. Ответ дайте в градусах.

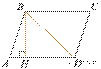17. Высота BH параллелограмма ABCD делит его сторону AD на отрезки AH  =  1 и HD  =  63. Диагональ параллелограмма BD равна 65. Найдите площадь параллелограмма.

18. На клетчатой бумаге с размером клетки 1см x 1см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

19. Какие из данных утверждений верны? Запишите их номера.

1)  Площадь квадрата равна произведению его диагоналей.

2)  Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.

3)  Вокруг любого параллелограмма можно описать окружность.