
Допустимые
значения переменных,
входящих в дробное выражение
Цели: формировать умение находить допустимые значения переменных, входящих в дробные выражения.
Ход урока
I. Организационный момент.
II. Устная работа.
– Подставьте вместо * какое-нибудь число и назовите полученную дробь:
а) ![]() ; б)
; б) ![]() ; в)
; в)
![]() ; г)
; г)
![]() ;
;
д) ![]() ; е)
; е) ![]() ; ж)
; ж) ![]() ; з)
; з)
 .
.
III. Объяснение нового материала.
Объяснение нового материала происходит в т р и э т а п а:
1. Актуализация знаний учащихся.
2. Рассмотрение вопроса о том, всегда ли рациональная дробь имеет смысл.
3. Вывод правила нахождения допустимых значений переменных, входящих в рациональную дробь.
При актуализации знаний учащимся
можно задать следующие
в о п р о с ы:
– Какую дробь называют рациональной?
– Всякая ли дробь является дробным выражением?
– Как найти значение рациональной дроби при заданных значениях входящих в неё переменных?
Для выяснения вопроса о допустимых значениях переменных, входящих в рациональную дробь, можно предложить учащимся выполнить задание.
З а д а н и е. Найдите значение дроби при указанных значениях переменной:
![]() при х = 4; 0; 1.
при х = 4; 0; 1.
Выполняя данное задание, учащиеся понимают, что при х = 1 невозможно найти значение дроби. Это позволяет им сделать следующий в ы в о д: в рациональную дробь нельзя подставлять числа, которые обращают её знаменатель в нуль (этот вывод должен быть сформулирован и произнесён вслух самими учащимися).
После этого учитель сообщает учащимися, что все значения переменных, при которых рациональное выражение имеет смысл, называют допустимыми значениями переменных.
Далее ставится вопрос: как находить допустимые значения переменных? При поиске ответа на этот вопрос учащиеся должны сформулировать р я д в о п р о с о в:
1) Если выражение является целым, то все значения входящих в него переменных будут допустимыми.
2) Чтобы найти допустимые значения переменных дробного выражения, нужно проверить, при каких значениях знаменатель обращается в нуль. Найденные числа не будут являться допустимыми значениями.
IV. Формирование умений и навыков.
1. № 10, № 11.
Ответ на вопрос о допустимых значениях
переменных, входящих в дробное выражение, может звучать по-разному. Например,
рассматривая рациональную дробь ![]() , можно сказать, что допустимыми
значениями переменной являются все числа, кроме х = 4, или что в
допустимые значения переменной не входит число 4, то есть х ≠ 4.
, можно сказать, что допустимыми
значениями переменной являются все числа, кроме х = 4, или что в
допустимые значения переменной не входит число 4, то есть х ≠ 4.
И та и другая формулировки являются верными, главное – следить за правильностью оформления.
О б р а з е ц о ф о р м л е н и я:
№ 11.
г) 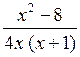
4х (х + 1) = 0
|
4х = 0 или х = 0 |
х + 1 = 0 х = –1 |
О т в е т: х ≠ 0 и х ≠ 1 (или все числа, кроме 0 и –1).
2. № 13.
3. № 14 (а, в), № 15.
При выполнении этих заданий следует обратить внимание учащихся на необходимость учёта допустимых значений переменных.
№ 15.
г) 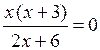
|
х (х + 3) = 0 х = 0 или |
2х + 6 ≠ 0 х = –3 х ≠ –3 |
О т в е т: х = 0.
4. № 17.
Следить за обоснованием всех рассуждений.
В классе с высоким уровнем подготовки можно дополнительно выполнить № 18 и № 20.
№ 18.
Р е ш е н и е
а)  .
.
Из всех дробей с одинаковым положительным числителем большей будет та, у которой знаменатель является наименьшим. То есть необходимо найти, при каком значении а выражение а2 + 5 принимает наименьшее значение.
Поскольку выражение а2 не может быть отрицательным ни при каких значениях а, то выражение а2 + 5 будет принимать наименьшее значение при а = 0.
О т в е т: а = 0.
б) 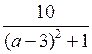 .
.
Рассуждая аналогично, получим, что необходимо найти то значение а, при котором выражение (а – 3)2 + 1 принимает наименьшее значение.
О т в е т: а = 3.
№ 20.
Р е ш е н и е
 .
.
Для ответа на вопрос предварительно нужно преобразовать выражение, стоящее в знаменателе дроби.
 .
.
Дробь будет принимать наибольшее значение,
если выражение (2х +
+ у)2 + 9 принимает наименьшее значение. Поскольку (2х
+ у)2 не может принимать отрицательные значения, то
наименьшее значение выражения (2х + у)2 + 9 равно 9.
Тогда значение исходной дроби равно ![]() = 2.
= 2.
V. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Какие значения называются допустимыми значениями переменных, входящих в выражение?
– Каковы допустимые значения переменных целого выражения?
– Как найти допустимые значения переменных дробного выражения?
– Существуют ли рациональные дроби, для которых все значения переменных являются допустимыми? Приведите примеры таких дробей.
Домашнее задание: № 12, № 14 (б, г), № 212.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.