Дослідження моделі витрати-випуск Леонтьєва

Дослідження моделі "витрати-випуск" Леонтьєва

В моделі Леонтьєва  діють підсистема виробництва продукції F та блок розподілу R_X, змінні X,Y,W (рис. 4.1).

Якщо позначити через X_i - валову продукцію і-ї галузі, Y_i - кінцеву продукцію і-ї галузі, W_i – проміжну продукцію і-ї галузі, то можна записати,

X_i  - W_i=Yі, .

Тут n - кількість галузей. В цій моделі діє припущення, що в кожній галузі виробництво здійснюється одним технологічним способом або галузі випускають однорідну продукцію. Нехай проміжна продукція і-ї галузі  дорівнює

,

де X_j - валова продукція j-ї галузі, ,  А_ij - кількість продукції і-ї галузі, що витрачається на виробництво одиниці продукції j-ї галузі.

Модель Леонтьєва  характеризується виробничою матрицею А

A=(A_ij),   ;  .

Ця матриця також зветься матрицею коефіцієнтів прямих матеріальних витрат.

В матрично-векторній формі модель має вигляд

(I-A)=,

де I – одинична матриця розміром (n×n),

 - вектор валової продукції (вектор випуску),

 - вектор кінцевої  продукції.

Вектор валової продукції можна знайти за формулою

=(I-A)^-1,

G=(I-A)^-1,

=G,

де G - обернена матриця Леонтьєва  або мультиплікатор Леонтьєва . Матриця G дорівнює

G=(G_ij), , .

Ця матриця зветься матрицею коефіцієнтів повних матеріальних витрат. Елемент G_ij показує потребу в валовій продукції і-ї галузі для виробництва одиниці кінцевої продукції j-ї галузі.

 Задача планування випуску валової продукції є перетворенням вектора кінцевої продукції  за допомогою матриці (I-A)^-1 у вектор валової продукції

=(I-A)^-1.

Виникає питання відносно умов, за яких існує така матриця (I-A)^-1 , що для будь-якого невід'ємного вектора , ≥0, вектор (I-A)^-1 також невід'ємний. Матриця А зветься невід'ємною, якщо всі її елементи є невід'ємними. Для економічних систем матриця А завжди невід'ємна, але вона має бути також продуктивною.

Умови продуктивності матриці А зв'язані з використанням одного з тверджень:

1)    максимальне власне число λ(A) матриці А менше 1;

2)    матриця (I-A) має невід'ємну обернену матрицю;

3)    матричний ряд

I+A+A²+...+A^r+… = ,

A⁰=I,

(так званий ряд Неймана матриці А) збігається, при цьому його сума дорівнює оберненій матриці (I-A)^-1

=(I-A)^-1,

4)    послідовні головні мінори матриці (I-A) додатні.

За даними А та  побудувати модель Леонтьєва  для двох галузей та знайти вектор валової продукції .

Для цього виконати такі дії:

1)    знайти матрицю (I-A), де І – одинична матриця

I=,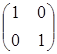

2)    обчислити визначник матриці |I-A|.

Для обчислення визначника можна скористатись правилом трикутника. Наприклад, для матриці В

В=,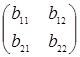

визначник дорівнює:

,

3)     знайти мінори для елементів матриці (I-A). Нагадаємо визначення мінору. Мінором M_ik зветься визначник (n-1) порядку, який одержуємо після викреслення і-рядка та k-стовпця, ;  . Наприклад, мінор М₁₁ дорівнює

,

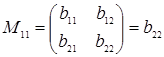4)    знайти алгебраїчні доповнення для елементів матриці (I-A).

Позначимо алгебраїчне доповнення ,; . Алгебраїчним доповненням  зветься мінор, який береться зі знаком (-1)^i+k

=(-1)^i+kM_ik.

Побудувати матрицю , приєднану до матриці (І-А). Матриця

     утворюється алгебраїчними доповненнями;   

5)    транспонувати матрицю ,

6)    знайти обернену матрицю (І-А)^-1 за формулою

                                                 , 

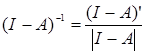7)    знайти вектор валової продукції

=(І-А)^-1,

8)    знайти міжгалузеві потоки продукції за формулою

X_ij= A_ijX_j,

(i,j)=1,2.

Результати звести до табл. 4.1.

Таблиця 4.1 - Результати розрахунків за моделлю  Леонтьєва