Эффективные методы изучения систем счисления в основной школе

Эффективные методы изучения систем счисления в основной школе

Димитрова Ольга Иннокентьевна, учитель информатики

МАОУ «Гимназии города Юрги»

Предмет исследования – методика изучения систем счисления в основной школе.

Проблема исследования –проанализировать и изучить психолого-педагогические и методические аспекты изучения систем счисления на уроках информатики в школе.

Цель исследования – определение эффективных путей и средств в изучении систем счисления.

Задачи исследования:

1.        Выявить влияет ли изучение систем счисления на развитие логического мышления и сообразительность школьников.

2.        Определить как процесс изучения систем счисления влияет на развитие интереса у школьников к предмету.

3.        Раскрыть теоретические и практические основы изучения систем счисления в школе.

4.        Провести практические эксперименты.

Методы исследования:

1.        Наблюдение за учебной деятельностью школьников в процессе изучения систем счисления.

2.        Изучение педагогической, методической литературы по исследованию данной темы.

       Гипотеза исследования: эффективность изучения систем счисления зависит от:

·           знания теоретического материала,

·           умения использовать его на практике,

Тема  «Математические основы информатики» знакомит  с  алгеброй логики  - булевой алгеброй, названной в честь основателя английского математика  Джорджа Буля. Увлекаясь философией он сделал вывод:  высказываниям можно присваивать значения 1 "истина" и 0 "ложь". Алгебра логики — это раздел математики и информатики,  изучающий  высказывания , со стороны истинности или ложности  и логических операций над ними. Алгебра логики позволяет закодировать любые утверждения, истинность или ложность которых нужно доказать. Значениям переменной в булевой алгебре соответствуют состояниям элементов микросхем компьютера или любого другого электронного устройства: сигнал присутствует (логическая "1") или сигнал отсутствует (логический "0").

На логических элементах, реализующих булевы функции, строятся логические схемы электронных устройств.

Законы булевой алгебры применяются и в программировании - при написании сложных логических условий и сложных запросов к базе данных.

Арифметические операции во всех позиционных систе­мах счисления выполняются по одним и тем же правилам.

Сложение. Рассмотрим сложение чисел в двоичной систе­ме счисления. В его основе лежит таблица сложения одно­разрядных двоичных чисел:

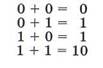
Нужно обратить внимание, что  при сложении двух единиц происходит переполнение младшего разряда и производится перенос в старший разряд. Переполнение разряда наступает тогда, когда величина числа в нем становится равной или большей основания - числа 2.

Сложение многоразрядных двоичных чисел происходит в
соответствии с таблицей сложения, с учетом возможных переносов из младших разрядов в старшие. В качестве примера сложим в столбик двоичные числа 110 ₂ и 11₂:

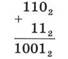
Проверим правильность вычислении сложением в деся­тичной системе счисления. Переведем двоичные числа в де­сятичную систему счисления и затем их сложим:

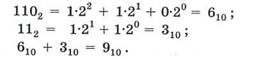
Теперь переведем результат двоичного сложения в деся­тичное число:

1001₂ = 1*2³ + 0*2² + 0*2¹ + 1*2° = 9₁₀ .

Сравним результаты — сложение выполнено правильно.

Объясним данный пример 1001₂ = 1*2³ + 0*2² + 0*2¹ + 1*2° = 9₁₀  с использованием программирования на языке QBASIC  в программе BASCOM-AVR IDE [2.0.7.1](см Рис.1)

Запустим программу  BASCOM-AVR  IDE .   Составим программу:

 Config  PORTD= Output  {сконфигурируем все порты (ножки контроллера АТ mega) на выход}

PORTD=0  {на все порты подается напряжение}

Do   {крутится в цикле}

PORTD=0  {на выход 30 подается единица 1*2°}

Waitms 100 млсек  {задержка диод горит желтым светом}

PORTD=9   {на выход 1 подается единица,  сумма=9  1001₂ = 1*2³ + 0*2² + 0*2¹ + 1*2° = 9₁₀  }

Waitms 100 млсек  задержка диод горит белым светом

Loop - прокрутка в цикле

End

Необходимо откомпилировать программу и сохранить файл, чтобы использовать его в работе схемы.

 Рис. 1

Запустим программу  Proteus 8 Professional   Рис.2. Выберим контроллер ATMEGA328P,откроем файл программы (Рис.1)

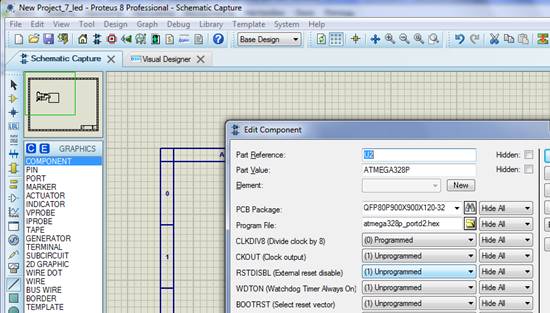
   Рис.2                                                      

Составим  схему.   Подключим к  светодиоды выходам:30-желтый, 31-зеленый,32-красный, 1-белый(на схеме контроллера указана степени двойки: PD0 ,  PD1, PD2,  PD3. По программе сумма PORTD=9. Согласно алгебры логики на подается сигнал на вход-30 загорается желтый светодиод  и вход-1-загорается белый светодиод , т.к.  сумма= 9

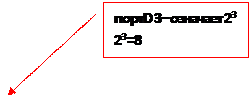
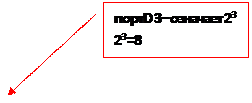
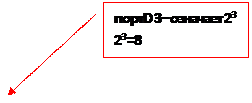
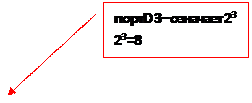
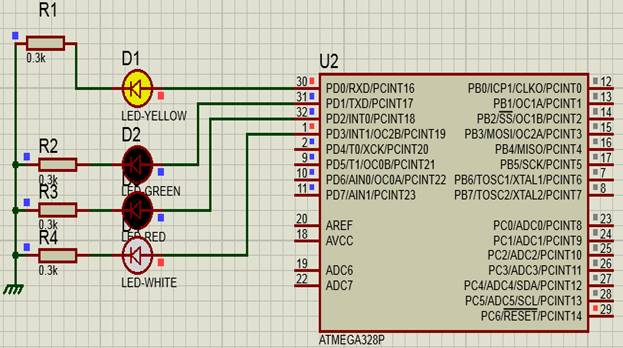
Рис. 3

Вывод : Проверить достоверность полученного результата, найти сумму вы­ражений с последующей проверкой: Порты работают на выход : PD0, PD1, PD2… PD7

Сумма двоичного кода=9  2⁰ =1   2³ =8   1001₂ = 1*2³ + 0*2² + 0*2¹ + 1*2° = 9₁₀ 

Практическое объяснение алгебры логики наиболее эффективный метод в изучении систем счисления на примере работы процессора ATMEGA328P.