Эталонное описание устройства Сфираль

Эталонное описание устройства Сфираль

© О.С. Басаргин

1.   Введение

Сфираль представляет собой топологически устойчивую структуру, состоящую из двух зеркально антисимметричных витков, соединённых Sобразным элементом. Она является самостоятельным объектом с возможностью проявления фрактальных свойств. Эти свойства могут быть выражены как в физической реализации устройства (например, при многоуровневом построении), так и в динамике процессов.

2.   Основные параметры Параметры:

•       R — радиус витка

•       h — расстояние между витками по оси z •           θ — угол поворота, начальное значение: 

•       S(θ) — функция S-образного соединения, заданная как: 

•       α,β — коэффициенты фрактальной вложенности

•       k — шаг витков Сфирали вдоль оси z, определяющий линейное смещение между уровнями структуры: 

•       ϕ — фазовый сдвиг: 

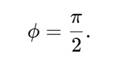
3.   Дифференциальные уравнения витков Эволюция радиуса и высоты:

Форма витков:

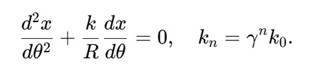
4.   Параметрические уравнения витков Верхний виток:

Нижний виток:

5.   S-образное соединение Уравнения:

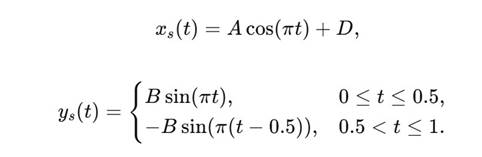
Функция S(θ) определяет параметры:

6.   Фрактальная зависимость (опционально)

Если Сфираль реализуется с фрактальной вложенностью, её параметры могут изменяться по законам:

Масштабирование угла:

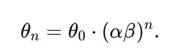
7.   Графическое представление и таблицы параметров 1. 3D-модель эталонной Сфирали o Основная форма с антисимметричными витками и S-образным соединением.

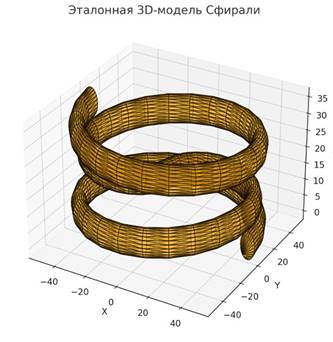
2.     Разделённый вид компонентов o Верхний и нижний витки отдельно. o S-образный элемент отдельно.

o  

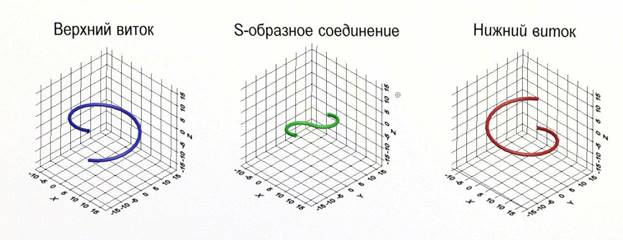
3.     Фрактальная структура o Визуализация уровней фрактального разложения.

o Как меняются радиус R_n и высота h_n при переходе к новым итерациям.

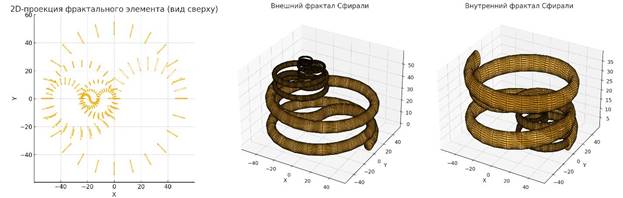
4.     График фазового угла ϕ в зависимости от уровня фрактальности o Изменение угла при переходе на новые уровни.

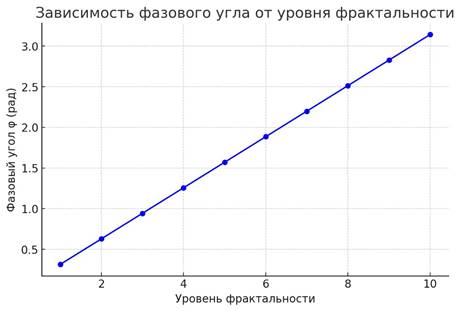
8.   Таблица параметров R,h,A,B,D,k на разных уровнях вложенности

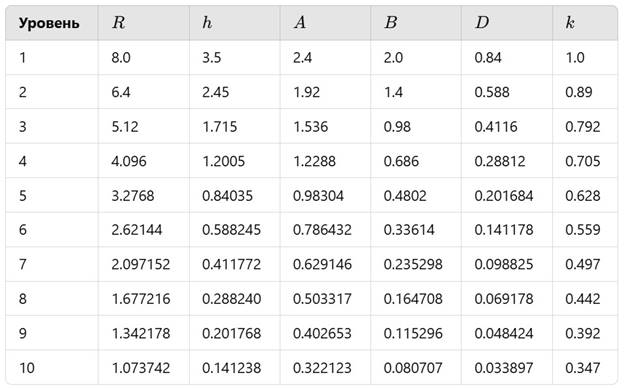
9.   Выводы

Сфираль является топологически устойчивой структурой, которая может быть реализована с фрактальной вложенностью, но не обязана ею обладать. S-образное соединение обеспечивает стабильность структуры, а параметры R,h,k допускают масштабирование для моделирования многоуровневых систем. Формулы сохраняют математическую корректность как для базовой конструкции, так и для её фрактальных модификаций. 

Выведенные математические уравнения и параметры могут быть применены для моделирования в квантовых вычислениях, физике, архитектуре и других областях.

Данный документ закрепляет эталонное математическое описание Сфирали и может использоваться в дальнейших исследованиях.