Сфираль — реальная форма времени

© О.С. Басаргин

Аннотация

Предлагается гипотеза о том, что физическое время имеет не

параметрическую, а топологическую природу и может быть описано как Сфираль — структура из двух зеркально антисимметричных витков, соединённых S-образной переходной зоной. В этой модели вводится параметр s (сфиральное время), через который можно переписать классические и квантовые уравнения движения. Показано, что феномены обратимости, коллапса, интерференции и стрелы времени получают новое толкование как фазовые переходы в пределах S-структуры. Предложены примеры моделей (свободная частица, осциллятор, квантовое состояние) и сценарии экспериментов. Модель даёт основания для переопределения времени как внутренней фазы эволюции систем, а не внешней шкалы. Обсуждаются границы применимости и направления дальнейших исследований, включая квантовую гравитацию, нейрофизиологию и динамику сознания.

1. Введение

Проблема природы времени остаётся фундаментальной нерешённой задачей современной физики. В классической механике и общей теории относительности время трактуется как внешняя параметрическая координата, задающая порядок событий. В квантовой механике оно вовсе не является оператором и остаётся неинтерактивным фоном. В этих подходах отсутствует конструктивное объяснение направленности времени (стрелы времени), природы настоящего момента и механизма перехода от потенциального будущего к актуальному прошлому.

Предлагается гипотеза: время не является параметром, а представляет собой топологически организованную структуру — Сфираль, состоящую из двух антисимметричных витков, соединённых S-образной переходной зоной. Такая структура способна задавать направленность, обратимость, множественность и внутреннюю метрику времени без апелляции к внешним координатам или энтропийным процессам.

2. Гипотеза

Сфиральная модель времени утверждает:

•       Время — это ориентированная пространственная структура, локально описываемая параметром s (сфиральное время),

•       Структура включает два зеркально антисимметричных витка — условно "прошлое" и "будущее" — и S-образную зону перехода, трактуемую как "настоящее".

•       Витки допускают обратимость (локальные законы сохраняют симметрию во времени), но глобальная антисимметрия даёт направленную эволюцию.

•       Фрактальная вложенность структуры описывает множественные временные уровни: локальные циклы, макроскопическое время, метавременные переходы.

•       Фазовый сдвиг φ(s) выражает момент согласования витков в S-зоне — он является аналогом событийности: точек перехода между возможным и актуальным.

В этой модели коллапс квантовой функции, термодинамическая стрелка времени, субъективное восприятие настоящего и космологическое расширение — разные проекции единой топологической структуры.

3. Математическая модель сфирального времени

Введём параметр s ∈ R, который определяет сфиральное время — позицию вдоль структурной траектории. В отличие от линейного времени t, параметр s определяет положение внутри витков и в S-зоне.

3.1. Геометрические функции Пусть:

•              R(s) — радиус текущего витка

•              h(s) — вертикальное смещение по оси z

•              θ(s) — угловая координата точки на витке

•              φ(s) — фазовый угол, определяющий положение в переходной зоне (S) Дифференциальные зависимости:

3.2. S-зона

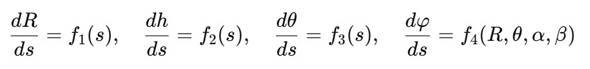
S-образное соединение задаётся функцией S(θ), обладающей антисимметрией:

Точка s = 0 — центральный переход: момент согласования и возможной инверсии.

3.3. Пространственно-временные траектории

Положение материальной точки можно задать как:

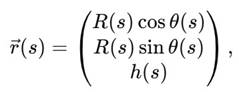
что определяет сфиральную траекторию.

Производные по s заменяют обычные временные производные:

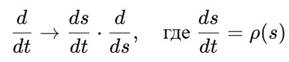
— локальная скорость прохождения сфирального времени. 

3.4. Динамические уравнения

Классические уравнения движения можно переписать в терминах сфирального времени:

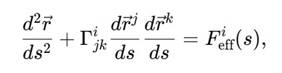
где Γⁱ_jk — связности в эффективной сфиральной метрике.

4. Примеры динамики в сфиральной модели времени

4.1. Свободная частица

В классической физике свободная частица описывается уравнением:

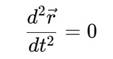
Переход к сфиральному времени s с параметрической скоростью

 даёт:

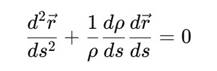
Это — уравнение геодезической с внешним трением, обусловленным изменением «скорости времени» ρ(s).

Геометрическая интерпретация:

Свободное движение в сфиральной модели — не линейное перемещение, а прохождение по геодезической линии на скрученной поверхности, где изменение ρ(s) отражает вложенную структуру.

Частный случай:

Пусть ρ(s) = ρ₀(1 + ϵ ⋅ sin φ(s)), тогда решение:

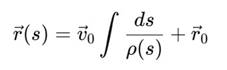
где 𝑣⃗₀ — начальный вектор скорости. В случае периодической модуляции φ(s) путь частицы становится квазипериодическим даже в отсутствии сил.

Следствие:

В сфиральной модели свободная частица может испытывать эффективное замедление, ускорение или возврат, обусловленные структурой времени, без внешнего воздействия.

4.2. Гармонический осциллятор в сфере времени

В классическом виде гармонический осциллятор описывается уравнением:

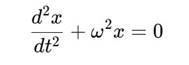
Переход к сфиральному времени s, при 

, приводит к уравнению:

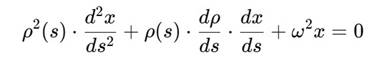
Это — аналог осциллятора со структурным демпфированием, зависящим от производной скорости сфирального времени.

Особый случай

Если ρ(s) = ρ₀(1 + ε ⋅ cos φ(s)), где φ(s) — фазовый угол сфирали, получаем осциллятор с периодически меняющимся коэффициентом трения:

Интерпретация

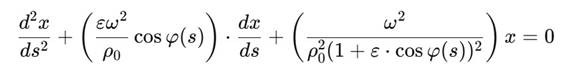
Осциллятор чувствует фазовую структуру времени. Его амплитуда, частота и затухание зависят не от внешней среды, а от положения внутри витка и переходной зоны.

При резонансном совпадении структуры φ(s) и внутренней частоты ω возможны:

•       Усиления (структурный резонанс);

•       Заглушения (структурная интерференция);

•       Фазовые замыкания (S-ловушки).

Предельный случай: S-зона

Вблизи s = 0 (переходная петля) можно разложить:

Уравнение переходит в квазипараметрически возбуждаемый осциллятор:

4.3. Квантовое состояние в сфере времени

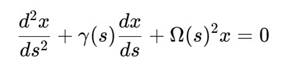
В квантовой механике эволюция состояния описывается уравнением Шрёдингера:

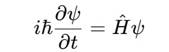
Переход к сфиральному времени:

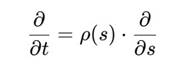
даёт модифицированное уравнение Шрёдингера:

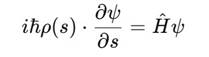
Введём фазовую развёртку:

тогда получаем уравнения для амплитуды и фазы:

Структурный коллапс

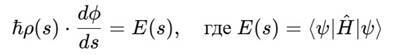
Предположим, что коллапс — это переход волновой функции через S-зону. Тогда вблизи s = 0 происходят:

•       Резкое изменение ϕ(s), соответствующее «актуализации»;

•       Сжатие амплитуды A(s) → A₀ ⋅ δ(s) при классическом исходе;

•       Сдвиг ρ(s) → 0 или максимум — в зависимости от модели спонтанного выбора.

Такой подход позволяет описывать коллапс не как разрыв, а как непрерывную фазовую деформацию на структурной петле.

Интерференция и S-структура

Пусть ψ = ψ₁ + ψ₂, два пути с фазами ϕ₁(s), ϕ₂(s). Если траектории проходят через разные ветви сфирали:

то их интерференция модулируется структурной разницей путей. При фазовом сдвиге на π, соответствующем антивиткам, наблюдается полное гашение.

4.4. Временная симметрия и разрыв стрелы времени в сфере S

Классическая физика (механика Ньютона, уравнение Шрёдингера, полевая теория без диссипации) инвариантна относительно обращения времени:

Однако в реальном мире наблюдаются процессы с чётко выраженной стрелой времени: рост энтропии, коллапс волновых функций, эволюция биологических систем, когнитивные последовательности восприятия.

Сфираль — источник временной ориентации

В сфиральной модели стрелу времени порождает антисимметричная структура витков, соединённых через S-петлю. Переход от одного витка к другому не инвариантен:

Но при этом:

•     геометрия сохраняется (вторичные производные симметричны); •           фазовые траектории претерпевают скачок ориентации, т.е. переход с "будущего" витка на "прошлый" — не тождественен.

Математическая формализация разрыва

Пусть функция ρ(s) (скорость прохождения времени) имеет асимметрию в окрестности S:

Тогда производные:

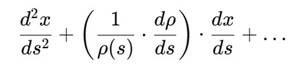
будут содержать разрыв в коэффициенте трения, ведущий к макроскопической необратимости — даже если микродинамика симметрична.

Пример: асимметрия фазового сдвига

Если φ(s) на S-петле проходит с фазовой задержкой или ускорением:

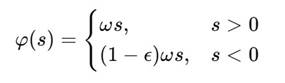
то при круговом цикле на фазовой диаграмме будет наблюдаться накопление некомпенсированной фазы — аналог необратимости в микроскопических кольцевых процессах (например, квантовых эффектов Холла).

Интерпретация

Разрыв стрелы времени возникает не из-за внешнего условия, а из-за встроенной антисимметрии переходной структуры времени. Даже при полной симметрии уравнений, наличие сфирального перехода формирует выбор ориентации, в которой происходит согласование состояний. Так реализуется естественное спонтанное нарушение T-инвариантности как топологическое свойство, а не динамическое возмущение.

5. Физические следствия и сценарии экспериментов

Сфиральная модель времени, основанная на антисимметричной структуре с переходной S-зоной, приводит к ряду потенциально проверяемых физических следствий. Ниже представлены направления, где структурное время может быть зафиксировано или воспроизведено экспериментально.

5.1. Коллапс как фазовый переход в S-зоне

Предсказание: квантовый коллапс — не мгновенный скачок, а фазовая перестройка в переходной зоне сфирали, происходящая в конечное время.

Эксперимент: наблюдение предколлапсной динамики с помощью слабых измерений, как в экспериментах Minev et al. (2019). Ожидаемая сигнатура: постепенное нарастание фазы φ(s) и сглаженный выход на определённое состояние.

5.2. Интерференция по разным ветвям сфирали

Предсказание: интерференционная картина зависит не только от фазовых разностей, но и от топологии прохождения путей (антивитки → гашение).

Эксперимент: двухщелевой эксперимент с пространственно разделёнными каналами, в которых реализуется антисимметрия времени (например, задержка или активный фазовый модулятор, создающий противоположные фазовые градиенты). Ожидается появление фазового сдвига, не сводимого к длине пути.

5.3. Структурное торможение свободной частицы

Предсказание: частица в вакууме может испытывать замедление или ускорение, связанное не с внешними силами, а с геометрией сфирального времени (ρ(s) ≠ const).

Эксперимент: наблюдение за движением сверххолодных атомов или нейтронов в условиях, где исключены поля, но сохраняется контроль над фазовой средой (оптическая решётка с временной модуляцией).

5.4. Эффекты антисимметрии при квантовом обходе S-петли

Предсказание: циклическое прохождение квантовой системы по структуре времени с переходом через S-зону может приводить к необратимому фазовому накоплению.

Эксперимент: квантовые кольцевые системы (сверхпроводящие кубиты в топологии SQUID), где модуляция фазового угла φ(s) приводит к наблюдаемому сдвигу интерференционной картины при возврате к исходной конфигурации.

5.5. Макроскопическая синхронизация через структуру времени

Предсказание: биологические или когнитивные процессы, имеющие собственную временную организацию, могут быть согласованы через сфиральную метрику — эффект коллективного входа в S-зону.

Эксперимент: синхронные измерения активности мозга (ЭЭГ, МЭГ) при предъявлении стимулов с фазовой структурой, вызывающей переход между когнитивными режимами (ожидание → осознание). Ожидается специфический фазовый профиль.

6. Выводы, границы применимости и перспективы

6.1. Сводка гипотезы

Предложена гипотеза: физическое время — не параметр, а топологически организованная структура, представленная в виде Сфирали с двумя антисимметричными витками и переходной S-зоной. Такое построение допускает наличие обратимости на локальном уровне и направленности — на глобальном, без введения внешней стрелы времени.

Введён параметр s — сфиральное время, в терминах которого переписаны уравнения классической и квантовой динамики. Показано, что основные физические процессы (движение, осцилляции, интерференция, коллапс) допускают формулировку в геометрии S-структуры и получают новые интерпретации.

6.2. Границы применимости

•       Гипотеза не отменяет стандартные уравнения, а преобразует их в другой параметрической форме, ориентированной на внутреннюю метрику времени.

•       Пока отсутствует строгая привязка к экспериментально измеряемым метрикам s, φ(s), ρ(s); необходима дальнейшая формализация.

•       Гипотеза не претендует на универсальное описание всех физических явлений, а предлагает новый слой понимания процессов, уже описываемых стандартной физикой.

6.3. Перспективы

1.     Формализация сфиральной метрики: построение полной псевдоримановой или финслеровой метрики времени с учётом витковой структуры.

2.     Интеграция с квантовой гравитацией: анализ роли S-структур в петлевых и причинно-дискретных моделях пространства-времени.

3.     Разработка численных моделей: интеграторы по s-параметру для моделирования систем с фазовой переходностью.

4.     Применение в нейронауке и когнитивных системах: моделирование переходов между состояниями осознания через фазовые S-петли.

5.     Разработка физически реализуемых устройств: сфиральные осцилляторы, сенсоры и временные преобразователи на основе контролируемых фазовых структур.

6.4. Заключение

Модель сфирального времени предлагает смену парадигмы: от параметра к структуре, от шкалы — к переходу. Это даёт возможность объединить внутренние аспекты динамики (фаза, переход, обратимость) с внешними проявлениями времени в наблюдаемой физике.

Дальнейшая разработка потребует как строгой математической теории, так и точной экспериментальной программы. Но даже на текущем уровне гипотеза позволяет переосмыслить природу временности как конструкта — не только в физике, но и в философии мышления, когниции и субъективного опыта.

Литературы

1.     Salem, Abdelmajid Ben Hadj. “SUR LE PROBLÈME DES TROIS CORPS ET LES EQUATIONS DE LA DYNAMIQUE -CHAPITRE 1 -NOUVELLE

EDITION NUMÉRIQUE.” Acta Mathematica, vol. 13, no. 1-2, 1889, pp. 5– 270.

2.     Ghirardi GC, Rimini A, Weber T. Unified dynamics for microscopic and macroscopic systems. Phys Rev D Part Fields. 1986 Jul 15;34(2):470-491. doi:

10.1103/physrevd.34.470. PMID: 9957165.

3.     Ramos, R., Spierings, D., Racicot, I. et al. Measurement of the time spent by a tunnelling atom within the barrier region. Nature 583, 529–532 (2020). https://doi.org/10.1038/s41586-020-2490-7  

4.     Minev ZK, Mundhada SO, Shankar S, Reinhold P, Gutiérrez-Jáuregui R, Schoelkopf RJ, Mirrahimi M, Carmichael HJ, Devoret MH. To catch and reverse a quantum jump mid-flight. Nature. 2019 Jun;570(7760):200-204. doi:

10.1038/s41586-019-1287-z. Epub 2019 Jun 3. PMID: 31160725.

5.     Pokorny, F., Zhang, C., Higgins, G., Cabello, A., Kleinmann, M., & Hennrich, M. (2019). Tracking the Dynamics of an Ideal Quantum Measurement. Physical review letters, 124 8, 080401 .

6.     Гарасько Г.И., Павлов Д.Г. (2007). Геометрия невырожденных поличисел. // Гиперкомплексные числа в геометрии и физике, №4(1(7)), с. 3–25.

7.     Черниговская Т.В. (2008). "Язык и сознание: что делает нас людьми?"

(проект «Публичные лекции Полит.ру», 20.11.2008)

8.     Басаргин, О. С. (2025). Временные Коды и Грядущее: Простое о сложном. Zenodo. https://doi.org/10.5281/zenodo.15134257

9.     Басаргин, О. С. (2025). Эталонное описание устройства Сфираль. Zenodo. https://doi.org/10.5281/zenodo.15133508