Областной конкурс учебно-методических комплектов и учебных средств, направленных на реализацию современных образовательных технологий и достижение учащимися ключевых компетенций 

 

 

«ИННОВАЦИОННЫЕ ОБРАЗОВАТЕЛЬНЫЕ РАЗРАБОТКИ - ИННОВАЦИОННОЙ ЭКОНОМИКЕ»

 

 

 

 

 

 

Рабочая тетрадь по математике

«За страницами учебника математики»

5 класс

 

 

 

 

 

Автор

Джинисян Н.Г.

Учитель математики МАОУ гимназия № 13 г. Томска

тел. 89131020991

 

 

Введение

 

Рабочая тетрадь по математике «За страницами учебника математики» является составляющей программы факультативного курса «За страницами учебника математики». Факультативный курс направлен на расширение и углубление знаний по предмету, развития логического мышления, привития интереса к предмету.

   Включенные вопросы в рабочую тетрадь дают возможность учащимся подготовиться к олимпиадам и различным математическим конкурсам. В рабочую тетрадь включены различные виды логических задач: - Круги Эйлера – задачи на пересечение или объединение множеств;

-   Задачи на переливание;

-   Задачи на взвешивание;

-   Задачи, решаемые с конца;

-   Задачи типа «Кто есть кто?» (метод графов, табличный способ).    Рабочая тетрадь имеет следующую структуру:

-   теоретический материал с описанием алгоритма решения задач;

-   решение некоторых задач;

-   задачи для самостоятельного решения.

   Свою работу обучающийся может выполнять последовательно, переходя от раздела к разделу. А может выбрать понравившийся раздел или отдельные задания.

   При написании данного пособия  использовались как свои наработки, так и переработанные разработки других авторов. Неполный список использованной литературы приведен в конце пособия.

   Факультативный курс с использованием рабочей тетради  был апробирован на учащихся 5 классов МАОУ гимназия № 13  г. Томска в 2010 – 2011 учебном году. Результатом работы являются следующие достижения обучающихся:

-   Финальный этап VII Международной Олимпиады по основам наук по предмету «Математика» - 2место (серебряная медаль), 3 место;

-   Международная математическая конкурс – игра «Кенгуру» - 10 место по Томской области;

-   Региональная математическая игра «Математическая биржа» для 5 классов – 1, 2 места;

-   Городская юниорская олимпиада по математике – 2 место.

 

 

 

 

 

 

 

 

 

 

 

Рабочая тетрадь по математике

 

 

 

 

 

Занимательная математика

 

 

        

5        класс

 

 

 

 

 

 

 

 

 

 

Дорогие ребята!

 

Данную рабочую  тетрадь можно использовать на занятиях факультатива, а так же для самостоятельной работы. В рабочую тетрадь включены различные виды логических задач. Логические задачи составляют обширный класс нестандартных задач. Сюда относятся, прежде всего, текстовые задачи, в которых требуется распознать объекты или расположить их в определенном порядке по имеющимся свойствам. При этом часть утверждений условия задачи может выступать с различной истинностной оценкой (быть истинной или ложной). К классу логических задач относятся также задачи на переливания и взвешивания (фальшивые монеты и т.п.).  

    Перед Вами будет поставлены следующие задачи:  

-   познакомиться с основными способами решения логических задач;   

-   на    примерах    конкретных         задач          выяснить:   Какие         методы        более эффективные? 

     В каждой теме вначале дан алгоритм решения и представлено решение некоторых задач. Вам предоставляется возможность поиска решений аналогичной задачи.

   Для овладения этими способами и приобретения соответствующего навыка предлагается ряд задач для самостоятельного решения.

    Свою работу можно выполнять последовательно, переходя от раздела к разделу. А можно выбрать понравившийся раздел или отдельные задания из него и получать удовольствие от самостоятельной работы.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

          Происхождение арифметики

     Велико значение математики в повседневной жизни человека. Без счета, без умения правильно складывать, вычитать, умножать и делить числа немыслимо развитие человеческого общества. Четыре арифметических действия, правила устных и письменных вычислений изучаются, начиная с начальных классов. Все эти правила не были выдуманы или открыты какимто одним человеком. Арифметика возникла из повседневной практики, из жизненных нужд людей в их трудовой деятельности. Арифметика развивалась медленно и долго. 

     Еще в самые отдаленные времена людям приходилось считать различные предметы, с которыми они встречались в повседневной жизни. Было время, когда человек умел считать только до двух. Число два связывалось с органами зрения и слуха и вообще с конкретной парой предметов. «Глаза» у индийцев, «крылья» у тибетцев означало также «два». Если предметов было больше двух, то первобытный человек говорил просто «много». Лишь постепенно человек научился считать до трех, затем до пяти, десяти и т. д.  

      С развитием производства и торговли счет распространяется на множества, содержащие все большее и большее число предметов (элементов). Люди в своей практической деятельности не могли обходиться без измерения расстояний, площадей земельных участков, вместимости сосудов и т. п. Потребность в измерениях привела к возникновению и развитию как приемов измерений, так и техники счета и правил действия над числами. 

 

     Таким образом, возникновение и развитие арифметики связано с трудовой деятельностью людей, с развитием общества. 

     Известно, что счет у нас ведется десятками: десять единиц образуют один десяток, десять десятков — одну сотню и т. д., иными словами: десять единиц первого разряда образуют одну единицу второго разряда, десять единиц второго разряда — одну единицу третьего разряда и т. д. 

     Но почему мы считаем именно десятками, то есть так возникла десятичная система счисления?  

     Подобно тому, как учатся считать по пальцам дети, так и люди на первых ступенях развития общества считали с помощью десяти пальцев рук. Поныне ведь говорят: «Перечесть по пальцам...». Отсюда — десятичная или десятеричная система счисления. 

     Однако были племена и народы, в частности в Африке, которые при счете пользовались лишь пятью пальцами одной руки, считали пятками: у них выработалась пятеричная система счисления, в которой основой служит число пять. В этой системе имеются названия для первых пяти чисел. Число «шесть», например, называлось «пять — один» и т.д. Следы пятеричной системы сохранились в скандинавских языках. Древнейшей из всех является двоичная система счисления, которой, как полагают, пользовались некогда древние египтяне. Следы другой, двадцатеричной системы остались поныне, например, в современном грузинском языке и во французском языке, в котором вместо «восьмидесяти» говорят «четырежды двадцать». Двадцатеричная система возникла у народов, считавших не только с помощью пальцев рук, но и пальцев ног. Этой системой пользовались также индейцы племени Майя. Древние вавилоняне пользовались шестидесятеричной системой счисления. В настоящее время почти все народы мира пользуются десятичной системой счисления.

 

 

 

Задачи для устной работы.

№ 1. Имеется ли самое малое натуральное число, самое большое?

№ 2. Назовите самое большое трехзначное число, самое маленькое трехзначное число.

№ 3. Написать наименьшее двухзначное число.

№ 4. С помощью цифр 3,6,2,4 написать наименьшее четырехзначное число. № 5. Написать наименьшее четырехзначное число, в котором все цифры различны.

Рассмотрите решение задачи № 6.

   Напишите наибольшее десятизначное число, в котором все цифры различны. Решение: Наибольшее из всевозможных десятизначных чисел с различными цифрами должно начинаться с наибольшей из всех цифр, т.е. с цифры 9. Замена цифры 9 любой другой цифрой лишь уменьшает число. Аналогично рассуждая относительно десятичных чисел, начинающихся с цифры 9, докажем, что следующей в записи искомого числа является цифра 8 – наибольшая из девяти оставшихся цифр и т.д. Таким образом, получим 9876543210.

   Используя рассуждения вышеизложенной задачи, решите следующую задачу.

№ 7. Напишите наименьшее десятизначное число, в котором все цифры различны.  1 023 456 789

Логическая пауза 

Встречаются двое учеников. Младший спрашивает старшего:

-   Ты умеешь делить?

-   Да.

-   Тогда раздели девять на три.

-   Пожалуйста.

(Пишет на доске: де – вя – ть).

№ 8. Сколькими способами можно представить число 10 в виде суммы четырех нечетных чисел?

№ 9. Сколькими способами можно представить число 50 в виде суммы двух четных чисел? Представления, отличающиеся порядком слагаемых, считать совпадающими. 

 

 

 

 

 

ü Задачи для самостоятельного решения

№ 10. В записи 88888888 поставьте между некоторыми цифрами знак сложения так, чтобы получилось выражение, значение которого равно 1 000. № 11. Вычислите сумму всех нечетных чисел, находящихся в первой тысяче.  № 12. Какой цифрой оканчивается произведение всех натуральных чисел от

1 до 81?   

№ 13. Какое слово из 11 букв все отличники пишут неправильно?  

ü Приготовьте  сообщения по темам «Числа натурального ряда и мистические суеверия», «Как люди научились считать».

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Круги Эйлера – задачи на пересечение       или объединение множеств

    Это новый тип задач, в которых требуется найти некоторое пересечение множеств или их объединение, соблюдая условия задачи. 

    Круги Эйлера — геометрическая схема, с помощью которой можно изобразить отношения между подмножествами, для наглядного представления. Метод Эйлера является незаменимым при решении некоторых задач, а также упрощает рассуждения. Однако, прежде чем приступить к решению задачи, нужно проанализировать условие. Иногда с помощью арифметических действий решить задачу легче. 

№ 14. Задача "Обитаемый остров" и "Стиляги"

     Некоторые ребята из нашего класса любят ходить в кино. Известно, что 15 ребят смотрели фильм «Обитаемый остров», 11 человек – фильм «Стиляги», из них 6 смотрели и «Обитаемый остров», и «Стиляги». Сколько человек смотрели только фильм «Стиляги»? Решение: Чертим два множества таким образом: 

 

 

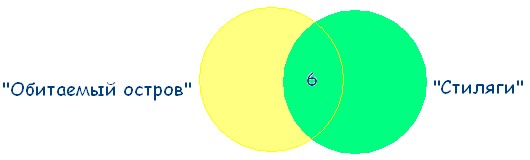
6 человек, которые смотрели фильмы «Обитаемый остров» и «Стиляги», помещаем в пересечение множеств. 

15 – 6 = 9 – человек, которые смотрели только «Обитаемый остров».  11 – 6 = 5 – человек, которые смотрели только «Стиляги».  Получаем: 

 

 

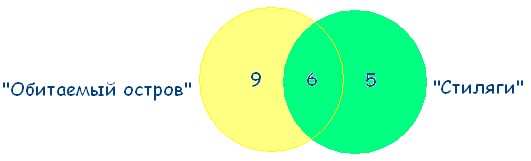
Ответ. 5 человек смотрели только «Стиляги».

№ 15. Задача. «Любимые мультфильмы»

          Среди школьников пятого класса проводилось анкетирование по любимым мультфильмам. Самыми популярными оказались три мультфильма: «Белоснежка и семь гномов», «Губка Боб Квадратные Штаны», «Волк и теленок». Всего в классе 38 человек. «Белоснежку и семь гномов» выбрали 21 ученик, среди которых трое назвали еще «Волк и теленок», шестеро – «Губка Боб Квадратные Штаны», а один написал все три мультфильма. Мультфильм «Волк и теленок» назвали 13 ребят, среди которых пятеро выбрали сразу два мультфильма. Сколько человек выбрали мультфильм «Губка Боб Квадратные Штаны»?  

____________________________________________________________

 

№ 16. Задача  «Мир музыки»

    В магазин «Мир музыки» пришло 35 покупателей. Из них 20 человек купили новый диск певицы Максим, 11 – диск Земфиры, 10 человек не купили ни одного диска. Сколько человек купили диски и Максим, и Земфиры? 

_____________________________________________________________

№ 17. Задача. «Гарри Поттер, Рон и Гермиона»

    На полке стояло 26 волшебных книг по заклинаниям. Из них 4 прочитал и Гарри Поттер, и Рон. Гермиона прочитала 7 книг, которых не читали ни Гарри Поттер, ни Рон, и две книги, которые читал Гарри Поттер. Всего Гарри Поттер прочитал 11 книг. Сколько книг прочитал Рон ?  

_______________________________________________________________

ü Задачи для самостоятельного решения № 18. Задача.  «Детский лагерь»

    В детском  лагере 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов; 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют, не увлекаются спортом, не занимаются в драмкружке? Сколько ребят заняты только спортом?  __________________________________________________________________

__________________________________________________________________

__________________________________________________________________

 

 

 № 19.  Задача. «Экстрим»

    Из 100 ребят, отправляющихся в детский оздоровительный лагерь, кататься на сноуборде умеют 30 ребят, на скейтборде – 28, на роликах – 42. На скейтборде и на сноуборде умеют кататься 8 ребят, на скейтборде и на роликах – 10, на сноуборде и на роликах – 5, а на всех трех – 3. Сколько ребят не умеют кататься ни на сноуборде, ни на скейтборде, ни на роликах? 

 

 

______________________________________________________________

№ 20. 

   Измените запись чисел 2 и 3 так, чтобы получилось число больше 2 и меньше 3.

_________________________________________________________________

№ 21.

   Если школьник купит 15 тетрадей, то у него останется 5 рублей. А на 16 тетрадей ему не хватит 10 рублей. Сколько стоит тетрадь и сколько денег у школьника?

__________________________________________________________________ __________________________________________________________________

ü Составьте и решите аналогичную задачу.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

       Задачи на переливание

     Рассмотрим еще один тип логических задач. Это задачи на переливания, в которых с помощью сосудов известных емкостей требуется отмерить некоторое количество жидкости.

№ 22. Задача. «Винни-Пух и пчелы»

    Однажды Винни-Пух захотел полакомиться медом и пошел к пчелам в гости. По дороге нарвал букет цветов, чтобы подарить труженицам пчелкам. Пчелки очень обрадовались, увидев мишку с букетом цветов, и сказали: «У нас есть большая бочка с медом. Мы дадим тебе меда, если ты сможешь с помощью двух сосудов вместимостью 3 л и 5 л налить себе 4 л!» Винни-Пух долго думал, но все-таки смог решить задачку. Как он это сделал? 

Решение: Как в результате можно получить 4 л? Нужно из 5-литрового сосуда отлить 1 л. А как это сделать? Нужно в 3-литровом сосуде иметь ровно 2 л. Как их получить? – Из 5-литрового сосуда отлить 3 л.  Решение лучше и удобнее оформить в виде таблицы: 

Ходы	1	2	3	4	5	6
5 л	5	2	2	-	5	4
3 л	-	3	-	2	2	3

 

     Наполняем из бочки 5-литровый сосуд медом (1 шаг). Из 5-литрового сосуда отливаем 3 л в 3-литровый сосуд (2 шаг). Теперь в 5-литровом сосуде осталось 2 литра меда. Выливаем из 3-литрового сосуда мед назад в бочку (3 шаг). Теперь из 5-литрового сосуда выливаем те 2 литра меда в 3-литровый сосуд (4 шаг). Наполняем из бочки 5-литровый сосуд медом (5 шаг). И из 5литрового сосуда дополняем медом 3-литровый сосуд. Получаем 4 литра меда в 5-литровом сосуде (6 шаг). Задача решена. 

Поиск решения можно было начать с такого действия: к трем литрам добавить 1 литр. Но тогда решение будет выглядеть следующим образом:   

Ходы	1	2	3	4	5	6	7	8
5 л	-	3	3	5	-	1	1	4
3 л	3	-	3	1	1	-	3	-

№ 23. Задача. «Бэтмен и Человек-Паук»

    Бэтмен и Человек-Паук никак не могли определить, кто из них самый главный супергерой. Что только они не делали: отжимались, бегали 100 метровку, подтягивались – то один победит, то другой. Так и не разрешив свой спор, отправились они к мудрецу. Мудрец подумал и сказал: «Самый главный супергерой – это не тот, кто сильнее, а тот, кто сообразительнее!

Вот, кто решит первым задачу, тот и будет самым-самым! Слушайте: имеются два сосуда вместимостью 8 л и 5 л. Как с помощью этих сосудов налить из источника 7 л живой воды?» Помогите вашему любимому герою решить эту задачу. Решение:

Ходы
8 л
5 л

 

№ 24. Задача «Молоко из Простоквашино»

   Дядя Федор собрался ехать к родителям в гости и попросил у кота Матроскина 4 л простоквашинского молока. А у Матроскина только 2 пустых бидона: трехлитровый и пятилитровый. И восьмилитровое ведро, наполненное молоком. Как Матроскину отлить 4 литра молока с помощью имеющихся сосудов? Решение: 

Ходы
8 л
3 л
5л

№ 25. Задача «Молоко и кофе»

    Имеется стакан кофе и стакан молока. Ложку молока перелили в кофе, полученную смесь тщательно перемешали. Ложку смеси перелили обратно в молоко. Чего больше: молока в кофе или кофе в молоке?  

Решение: Примем начальный объем жидкости в каждом стакане за 1. Таким образом, после всего в обоих стаканах имеется единичный объем кофе и единичный объем молока. Поскольку из первого стакана перелили во второй одну ложку, а затем из второго в первый перелили такую же ложку, то в конце в каждом стакане снова будет объем жидкости, равный 1. Пусть объем кофе в первом стакане после переливания равен x, а во втором стакане – y. Тогда молока во втором стакане – (1-y). Поскольку в двух стаканах всего единичный объем кофе, x+y=1. Отсюда x=1-y, т.е. кофе в стакане с молоком и молока в стакане с кофе поровну.  Ответ. Поровну.

 

ü Задачи для самостоятельного решения № 26.   Задача «Карлсон и варенье»

    У Карлсона есть ведро варенья, оно вмещает 7 литров. У него есть 2 пустых ведерка - 4-литровое и 3-литровое. Помогите Карлсону отлить 1 литр варенья к чаю в меньшее (3-литровое) ведерко, оставив 6 литров в большом (7-литровом) ведре.  Решение:

Ходы
7 л
4 л
3л

 

 

 

 

№27. Имеются шестилитровая банка сока и две пустые банки: трех- и четырехлитровая. Как налить 1 литр сока в трехлитровую банку? 

 

 

 

№ 28.  Имеются два пустых бидона – трехлитровый и пятилитровый. Как, пользуясь этими бидонами, набрать из реки ровно 1л воды?

 

 

№ 29. Как налить равно 4 л воды, пользуясь двумя пустыми ведрами объемом 5 л и 7 л, водопроводным краном для наливания и раковиной для наливания.

 

 

 

 № 30.  Можно ли, пользуясь двумя пустыми ведрами объемом 12л и 9л, набрать из речки ровно 4 л воды?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачи на взвешивание

    Задачи на взвешивание - достаточно распространённый вид математических задач. В таких задачах от решающего  требуется локализовать отличающийся от остальных предмет по весу за ограниченное число взвешиваний. Поиск решения в этом случае осуществляется путем операций сравнения, правда, не только одиночных элементов, но и групп элементов между собой.

№ 31. Задача «Буратино и Кот Базилио»

    У Буратино есть 27 золотых монет. Но известно, что Кот Базилио заменил одну монету на фальшивую, а она по весу тяжелее настоящих. Как за три взвешивания на чашечных весах без гирь Буратино определить фальшивую монету? 

Решение:

    Разделим монеты на 3 кучки по 9 монет. Положим на чаши весов первую и вторую кучки; по результату этого взвешивания мы точно узнаем, в какой из кучек находится фальшивка (если весы покажут равенство, то она - в третьей кучке). Теперь, аналогично, разделим выбранную кучку на три части по три монеты, положим на весы две из этих частей и определим, в какой из частей находится фальшивая монета. Наконец, остается из трех монет определить более тяжелую: кладем на чаши весов по 1 монете - фальшивкой является более тяжелая; если же на весах равенство, то фальшивой является третья монета из части. Задача решена.

№ 32.  Среди 18 монет одна фальшивая. Настоящие монеты весят одинаково, фальшивая монета отличается по массе от настоящих. За какое наименьшее число взвешиваний на правильных чашечных весах без гирь можно определить, легче или тяжелее фальшивая монета, чем настоящая? Решение:

    Занумеруем монеты. Разобьем множество монет на 3 кучки по 6 монет в каждой.

   При первом взвешивании положим на одну чашу весов все монеты 1 кучки, на другую – второй. Возможны 2 случая.

1                   случай: весы оказались в равновесии. Тогда фальшивая монета в третьей кучке. Теперь положим на одну чашу весов первую кучку монет, на другую – третью. Если, например, третья кучка перетянет, то фальшивая монета тяжелее настоящей.

2                   случай. Пусть при первом взвешивании весы были не в равновесии. Тогда фальшивая монета находится или в первой кучке или во второй. Следовательно все монеты третьей кучки настоящие. Положим на одну чашу весов первую кучку монет, на другую – третью. Если весы оказались в неравновесии, то фальшивая монета в первой кучке, и второе взвешивание покажет, легче она или тяжелее, чем настоящая. Если же весы оказались в равновесии, то фальшивая монета во второй кучке, и по первому взвешиванию также можно определить, легче она или тяжелее настоящей.

 

 

 

1 вариант			результат	Фальшивая монета
1 взвешивание	1 кучка	2 кучка	равновесие	В третьей кучке
2 взвешивание	1 кучка	3 кучка	неравновесие	Определяем вес
2 вариант
1 взвешивание	1 кучка	2 кучка	Неравновесие	1 кучка
2 взвешивание	1 кучка	3 кучка	неравновесие	1 кучка, определяем вес
3 вариант
1 взвешивание	1 кучка	2 кучка	Неравновесие	2 кучка
2 взвешивание	1 кучка	3 кучка	неравновесие	По результатом первого взвешивания определяем вес фальш. монеты

 

Ответ: достаточно 2 взвешивания.

 

 

 

 

 

          

№  33. Задача «Золушка»

     Мачеха послала Золушку на рынок. Дала ей девять монет: из них 8 настоящих, а одна фальшивая – она легче чем настоящая. Как найти ее Золушке за два взвешивания?  

______________________________________________________________

______________________________________________________________ ______________________________________________________________

 

 

 

 

№ 34. Задача  «Фальшивая монета»

   Среди 101 одинаковых по виду монет одна фальшивая, отличающаяся по весу. Как с помощью чашечных весов без гирь за два взвешивания определить, легче или тяжелее фальшивая монета? Определить фальшивую монету не требуется. 

__________________________________________________________________

__________________________________________________________________

_______________________________________________________________ ü Задачи для самостоятельного решения

ü  

№ 35. Задача «Дядюшка Скрудж»

   Дядюшке  Скруджу принесли 8 одинаковых по виду монет, одна из которых не золотая, а фальшивая и легче других. Помогите Скруджу определить фальшивую монету. Какое минимальное число взвешиваний ему потребуется? 

__________________________________________________________________ ______________________________________________________________

№ 36.  Среди 18 монет одна фальшивая. Настоящие монеты весят одинаково, фальшивая монета отличается по массе от остальных. За какое наименьшее число взвешиваний на правильных чашечных весах без гирь можно определить, легче или тяжелее фальшивая монета, чем настоящая? (находить фальшивую монету не нужно). 

______________________________________________________________

№ 37.  Из 4 монет одна тяжелее остальных, имеющих одинаковый вес.

Можно ли узнать с помощью двух взвешиваний на весах с двумя чашечками без гирь?

______________________________________________________________

 

 

 

№ 38.  Из 27 монет одна – фальшивая. Она легче остальных. Можно ли найти ее за 3 взвешивания?

______________________________________________________________

№ 39.  Какой вес должна иметь каждая из гирь для того, чтобы с их помощью можно было взвесить любое целое число килограммов от 1 кг до 10 кг на чашечных весах (гири можно ставить на обе чашки). Обоснуйте свой ответ. _______________________________________________________________

_______________________________________________________________

№ 40. Восстановите запись: 

*8 • * =8 * * 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Задачи, решаемые с конца

Недостаточно лишь понять задачу, необходимо желание решить ее. Без сильного желания решить трудную задачу невозможно, но при наличии такового – возможно.

Где есть желание, найдется путь!

Пойя Д.     Имеется много интересных задач, которые удобно решать,  начиная с конца. Рассмотрим, например, следующую задачу. 

    № 41.   Двадцать четыре  спички разделили на три неравные кучки. Если из первой кучки переложить во вторую столько спичек, сколько было в этой второй кучке, затем из второй кучки переложить в третью столько, сколько было в этой третьей, и наконец из третьей переложить в первую столько спичек, сколько в этой первой кучке осталось, то после всех перекладываний число спичек во всех кучках будет одинаково. Требуется узнать, сколько было спичек в каждой кучке первоначально. 

 Решение:  После всех перекладываний в каждой кучке стало по 8 спичек.      Перед этим в первую кучку было добавлено столько спичек, сколько их там имелось, то есть число спичек в первой кучке было удвоено. Так как в ней стало 8 спичек, то перед этим там было 4 спички, а 4 спички переложены из третьей кучки. Следовательно, до последнего перекладывания в первой кучке было 4, во второй – 8, а в третьей – 12 спичек. 

    Второй раз из второй кучки в третью переложили столько спичек, сколько в третьей имелось. Значит, 12 – это удвоенное число спичек, бывших в третьей кучке до второго перекладывания. Следовательно, можно узнать число спичек в каждой кучке после первого перекладывания: в третьей – 12 : 2 = 6 спичек; во второй – 8 + 6=14 спичек; в первой – 4 спички. 

   Так как первый раз во вторую кучку переложили из первой 14 : 2 = 7 спичек, то первоначально в первой кучке было 11, во второй – 7, а в третьей – 6 спичек.

№ 42. Задача  «Алла Пугачева и Кристина Орбакайте»

    Алле Пугачевой и ее дочери Кристине Орбакайте вместе 98 лет. Кристина родилась, когда Алле Пугачевой было 22 года. Какого возраста обе певицы?  __________________________________________________________________

______________________________________________________________

 

 

 

№ 43. Задача   «Задуманное число»

          Я задумала число, умножила его на два, прибавила три и получила 17. Какое число я задумала?

______________________________________________________________

 

 

№ 44. Задача   « Маша и медведи»

      Маша принесла своим друзьям медведям торт. Известно, что старший медведь съедает торт за 2 дня, средний медведь – за 3 дня, младший медведь

– за 6 дней. За сколько дней три медведя вместе съедят торт?

_____________________________________________________________ _____________________________________________________________

  

№ 45.  Задача   «Яблоки»

    Трое мальчиков имеют по некоторому количеству яблок. Первый мальчик дает другим столько яблок, сколько каждый из них имеет. Затем второй мальчик дает двум другим столько яблок, сколько каждый из них теперь имеет; в свою очередь и третий дает каждому из двух других столько, сколько есть у каждого в этот момент. После этого у каждого из мальчиков оказывается по 8 яблок. Сколько яблок было у каждого мальчика вначале? Решение: Решаем задачу с конца с помощью таблицы.

 

 

Номер мальчика	1	2	3
Число яблок в конце	8	8	8

 

__________________________________________________________________ _________________________________________________________________

 

 

 

№ 46. Задача «Крестьянин и царь».    

Крестьянин пришел к царю и попросил: «Царь, позволь мне взять одно яблоко из твоего сада». Царь ему разрешил. Пошел крестьянин к саду и видит: весь сад огорожен тройным забором. Каждый забор имеет только одни ворота, и около каждых ворот стоит страж. Подошел крестьянин к первому стражу и сказал: «Царь разрешил мне взять одно яблоко из сада». «Возьми, но при выходе должен будешь отдать мне половину яблок, что возьмешь, и еще одно», - поставил условие страж. Это же повторили ему второй и третий, которые охраняли другие ворота. Сколько яблок должен взять крестьянин, чтобы после того, как отдаст положенные части трем стражам, у него осталось одно яблоко?  __________________________________________________________________

________________________________________________________________

 

ü Задачи для самостоятельного решения № 47. Задача  «Отгадай число»

    Я задумал число, умножил его на 7, прибавил 15 и получил 50. Какое число я задумал?

 ____________________________________________________________

№ 48. Задача  «Черт и бездельник»

    Однажды черт предложил бездельнику заработать. «Как только ты перейдешь через этот мост, - сказал он, - твои деньги удвоятся. Можешь переходить по нему сколько хочешь раз, но после каждого перехода отдавай мне за это 24 рубля». Бездельник согласился и … после третьего перехода остался без денег. Сколько денег у него было сначала? 

 

 

№ 49.  Задача  «Туристы»

     Группа туристов отправилась в поход. В первый день они прошли 1/3 пути, во второй - 1/3 остатка, в третий - 1/3 нового остатка. В результате им осталось пройти 32 км. Сколько километров был маршрут туристов? __________________________________________________________________ __________________________________________________________________ ___

 № 50.  Задача «Гуси»

    Над озерами летели гуси. На каждом озере садилась половина гусей и еще полгуся, остальные летели дальше. Все сели на семи озерах. Сколько было гусей? 

__________________________________________________________________ __________________________________________________________________

 

№ 51. Задача  «Магия чисел»

    Я задумал число, прибавил к нему 5, потом разделил сумму на 3, умножил на 4, отнял 6, разделил на 7 и получил число 2. Какое число я задумал. 

_____________________________________________________________

 

 

 

 

 

 

 

 

   Задачи типа "Кто есть кто?"

Как без математических наук

                                                                  проводит свои линии паук. 

                                                                                                          А.Поуп 

      Задачи типа «Кто есть кто?» - это самые что ни на есть логические задачи. Смысл задач под кодовым названием «Кто есть кто?» довольно прост. Вам даны отношения между предметами и следуя по цепочке этих отношений, вы приходите к правильному результату. 

    Существует несколько методов решения задач типа «Кто есть кто?». Один из методов решения таких задач – метод графов. Второй способ, которым решаются такие задачи – табличный способ.

Метод графов

Один из способов решения задач типа «Кто есть кто?» - метод графов.  Граф – это несколько точек, часть которых соединены друг с другом отрезками или стрелками (в этом случае граф называется ориентированным). 

Рассмотрим метод графов на примере решения задачи. 

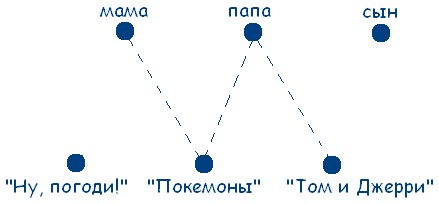
№ 52. Задача  «Любимые мультфильмы»

    Жила-была одна дружная семья: мама, папа и сын. Они все любили делать вместе. Но вот мультфильмы любили разные: «Ну, погоди!», «Покемоны», «Том и Джерри». Определите, какой мультфильм любит каждый из них, если мама, папа и любитель мультфильма «Покемоны» никогда не унывают, а папа и любитель мультфильма «Том и Джерри» делают зарядку по утрам? 

Решение:

    Рассмотрим множество людей: мама, папа, сын и множество мультфильмов «Ну, погоди!», «Покемоны», «Том и Джерри». Обозначим элементы этих двух множеств точками: 

     Если точке из одного множества соответствует точка другого множества, будем соединять эти точки сплошной линией, если не соответствует – то штриховой. Заметим, что по условию задачи у человека только один любимый мультфильм. 

Учитывая данные задачи, получаем следующую схему: 

 

   Из условия задачи следует, что нужно найти единственно возможное соответствие между элементами двух множеств. 

Ø Правило: если какая-то точка оказывается соединенной с двумя точками другого множества штриховыми линиями, то с третьей точкой она должна быть соединена сплошной. 

Поэтому граф на рисунке будет выглядеть следующим образом: 

 

 

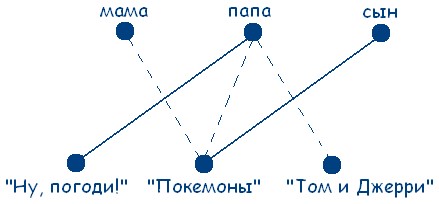
    Теперь мы установили, что папа любит мультфильм «Ну, погоди!», сын – «Покемоны». В обоих множествах остается только по одной точке, следовательно мама любит мультфильм «Том и Джерри». Задача решена. 

Ø Таким же способом можно находить соответствие между тремя множествами. Тогда при решении мы можем получить треугольники трех видов: 

а) все стороны являются сплошными отрезками (решение задачи); 

б) одна сторона – сплошной отрезок, а две другие – штриховые; 

в) все стороны – штриховые отрезки. 

    Таким образом, нельзя получить треугольник, у которого бы две стороны были сплошными отрезками, а третья – штриховой отрезок. 

№ 53.

    Три подруги были в белом, красном и голубом платьях. Их туфли были тех же трех цветов. Только у Тамары цвета платья и туфель совпадали. Валя была в белых туфлях. Пи платье, ни туфли Лиды не были красными.

Определить цвет платья и туфель каждой из подруг. 

Решение

   Изобразим три множества: множество подруг, множество платьев, множество туфель.

____________________________________________________________ ____________________________________________________________

 

 

 

 Возникает вопрос: так уж нужны ли графы в этих задачах? Разве нельзя прийти к решению логическим путем? Можно, но графы придали условиям наглядность. Упростили решение и выявили сходство задач.

    Есть задачи, графы которых имеют 100 и более вершин. А ведь именно такие задачи приходится решать современным инженерам и экономистам. Тут без графов не обойтись. Сейчас почти в любой отрасли науки и техники встречаешься с графами: в электротехнике – при построении молекул и их цепочек; в экономике – при решении задач выбора оптимального пути для потоков грузового транспорта.

   Теория графов – наука сравнительная молодая. Первая работа по теории графов принадлежит Леонарду Эйлеру. Она появилась в 1736 году в публикациях Петербургской Академии Наук и начиналась с рассмотрения задачи о кенигсбергских мостах.

Ø Приготовьте сообщение о биографии Л.Эйлера, рассмотрите задачу о кенигсбергских мостах.

Второй способ, которым решаются такие задачи - табличный способ.

Табличный способ

    Табличный способ решения логических задач также прост и нагляден, но его можно использовать только в том случае, когда требуется установить соответствие между двумя множествами. Он более удобен, когда множества имеют по пять-шесть элементов. Рассмотрим табличный способ на примере решения задачи.     Рассмотрим табличный способ на примере решения задачи.  № 54. Задача  «Футбол»

    Четыре футбольных команды: итальянская команда «Милан», испанская – «Реал», российская – «Зенит», английская – «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Джон. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно: 

а) Зенит не тренируется у Джона и Антонио. 

б) Милан обещал никогда не брать Джона главным тренером. 

Решение. 

   Решая задачу, мы заведомо знаем, что у каждой команды только один тренер. 

 Чтобы решить задачу табличным способом, нужно знать следующие правила: 

1.В каждой строке и в каждом столбце таблицы может стоять только один знак соответствия (например «+»). 

2.Если в строке (или столбце) все «места», кроме одного, заняты элементарным запретом (знак несоответствия, например «-»), то на свободное место нужно поставить знак «+»; если в строке (или столбце) уже есть знак «+», то все остальные места должны быть заняты знаком

«-». 

    Таким образом, решение будет доведено до конца, когда мы сумеем разместить по одному плюсу в каждом ряду и колонке, обозначив таким образом, тренеров всех четырех команд. 

         А теперь приступаем к решению задачи. 

    Нам известно, что ни у одной из команд национальность тренера и команды не совпадали, а также, что «Зенит» не тренируется у Джона и Антонио, значит у этой команды тренер не Джон и не Антонио; а «Милан» обещал никогда не брать Джона тренером, значит у команды «Милан» тренер не Джон. Если проставить соответствующие минусы, то таблица будет выглядеть так: 

 

Таким образом, становится ясно, что у «Зенита» тренер Родриго (методом исключения).  Поставим «+» напротив Родриго в колонке «Зенит» и заполним свободные клетки в его ряду минусами:

 

 

Теперь можно сделать вывод, что тренер «Милана» – Николай. Поставим «+» напротив Николая и заполним свободные клетки в его ряду минусами. Теперь видно, что «Челси» тренирует Антонио, а «Реал» - Джон.      Ответ. Российская команда «Зенит» тренируется у испанца Родриго; итальянская команда «Милан» тренируется у русского Николая; английская команда «Челси» тренируется у итальянца Антонио; испанская команда

«Реал» тренируется у англичанина Марка.

 

 

 

№ 55. Задача  «Компьютерные игры»

     В компьютерном классе на уроке информатики, во время отсутствия учителя, пять ребят – Максим, Настя, Саша, Рома, Сережа – отвлеклись от нужной работы и стали играть в такие игры: пасьянс «Паук», гонки, сапер, «Марио», тетрис. Каждый из них играл только в одну игру.  

•  Саша думал, что в «Марио» играет Настя. 

•  Настя предполагала, что Рома играет в тетрис, а Максим – в гонки. 

•  Рома считал, что Сережа играет в гонки, а Саша – в сапера. 

•  Максим думал, что Настя раскладывает пасьянс «Паук», а в «Марио» играет Рома. 

   В результате оказалось, что все они ошиблись в своих предположениях. Кто и во что играл? 

___________________________________________________________________

___________________________________________________________________

№ 56.Задача  «Мушкетёры»

    Атос, Портос, Арамис и Д’Артаньян – четыре талантливых молодых мушкетёра. Один из них лучше всех сражается на шпагах, другой не имеет равных в рукопашном бою, третий лучше всех танцует на балах, четвертый без промаха стреляет с пистолетов. О них известно следующее: 

•  Атос и Арамис наблюдали на балу за их другом – прекрасным танцором. 

•  Портос и лучший стрелок вчера с восхищением следили за боем рукопашника. 

•  Стрелок хочет пригласить в гости Атоса. 

•  Портос был очень большой комплекции, поэтому танцы были не его стихией. 

Кто чем занимается? 

___________________________________________________________________

___________________________________________________________________

№ 57. Задача  «Три товарища»

    Три товарища – Владимир, Игорь и Сергей окончили один и тот же институт и преподают математику, физику и литературу в школах Тулы. Рязани и Ярославля. Владимир работает не в Рязани, Игорь – не в Туле. Рязанец преподает не физику, Игорь не математику, туляк преподает литературу. Какой предмет и в каком городе преподает каждый?

 

Города		Тула	Рязань	Ярославль
Игорь
Сергей
Владимир
Предметы		математика	физика	литература
Тула
Рязань
Ярославль

Ответ: ________________________________________________

ü Задачи для самостоятельного решения

№   58.   

   Встретились три друга – Белов, Чернов и Серов. Чернов сказал другу, одетому в серый костюм: «Интересно, что на одном из нас белый костюм, на другом – серый и на третьем – черный, но на каждом костюм цвета, не соответствующего фамилии». Какой цвет костюма у каждого из друзей? Решение:

Ответ: __________________________________________________  № 59. Задача «Контрольная работа».

    Написав контрольную работу по математике, три сестры сообщили родителям следующее. Ира: « Я написала не на пять». Лиза: «Я написала не на три». Светлана: «На этот раз я написала на пять». После проверки работ выяснилось, что сестры получили разные положительные оценки и из трех высказываний сестер только одно верное. Какую оценку получила за контрольную работу каждая? Решение :

	3	4	5
Ира
Лиза
Светлана

 Пусть Светлана говорит правду:

	3	4	5
Ира
Лиза
Светлана

 

	3	4	5
Ира
Лиза
Светлана

 

Ответ: ____________________________________________________ Список литературы  

1.     А.В.Фарков «Внеклассная работа по математике 5 – 11 классы», Москва, 2008.

2.     А.В.Фарков «Математические олимпиады», Москва, 2009.

3.     З.Н. Альхова, А.В. Макеева «Внеклассная работа по математике», Саратов, 2001.

4.     Е.В.Галкин «Нестандартные задачи по математике. Задачи логического характера», Просвещение – Учебная литература» – 1996г.

5.     Е. В. Галкин, Нестандартные задачи по математике. Задачи логического характера. Книга для учащихся 5-11 кл.- М.: Просвещение, 1996.

6.     Журнал «Математика в школе». № 3, 1995.

7.     И. С. Петраков «Математические олимпиады школьников», М.    Просвещение, 1990.

8.     П. Ю. Германович «Математические викторины»Содержание. - М, Просвещение, 1989.

9.     Т.В. Введенская, Е.И. Лященко «Математика, 5 класс: учимся решать задачи, Дидактика, 1995.

10. Я. Н. Виленкин «За страницами учебника математики» - М., 1996.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Содержание

 

 

Предисловие …………………………………………………………………….2

Происхождение арифметики ……………………………………………….. 3-6

Круги Эйлера – задачи на пересечение или объединение множеств…   7 – 10

Задачи на переливание……………………………………………………11 – 15 Задачи на взвешивание…………………………………………………….16- 20

Задачи, решаемые с конца …………………………………………………21-25

Задачи типа «Кто есть кто?» (метод графов)……………………………. 26-29

Табличный способ………………………………………………………...30 – 35 Литература……………………………………………………………………..36