
7 класс 1 вариант
1. Вычислите x4 − 2(x + 3)2 + 4 при x = 3.
A) 12 B) 13 C) − 12 D) 120
E) Варианты A – D неверны
2. Кусок мыла и изначально имел обычную форму «кирпич» (каждая грань которого – прямоугольник). За время использования кусок мыла уменьшился, оставшись по форме «кирпичом», но каждая его сторона сократилась в 1,3 раза по сравнению с изначальными размерами. Во сколько раз уменьшился объём куска мыла?
A) 1,69 B) 0,79 C) 2,197 D) 1,3 E) 2,3
3. Решите уравнение:
![]() 2x + 1−3x = 1,5
2x + 1−3x = 1,5
A) 19 B) 12 C) 337 D) 29 E) 0
![]() 4. Найдите положительное x,
которое удовлетворяет условию (
3x)2 + 4 = 1
4. Найдите положительное x,
которое удовлетворяет условию (
3x)2 + 4 = 1
A) 0,5 B) 3,5 C) 7 D) 6,3 E) 5
5. В равнобедренном треугольнике ABC угол B равен 120. BH – высота треугольника ABC , BN – биссектриса треугольника ABH , BM – биссектриса треугольника CBH . Длина отрезка BN равна 7. Найдите длину стороны AC .
A) 14 B) 6 C) 21 D) 10 E) Варианты A – D неверны
6. Найдите сумму всех целых чисел x, которые удовлетворяют условию |x−33| < 1,3, но не удовлетворяют условию x2 < 5 .
A) 18 B) 12 C) 3 D) 7 E) -3
7. В наборе юного геометра даны палочки длиной
1, 2, 3, 5 и 6 см. Сколько различных треугольников можно составить из палочек этого набора (не обязательно одновременно).
A) 15 B) 0 C) 2 D) 3 E) Варианты A – D неверны
8. Мишенью с номером 1 называется квадрат с вершинами (1; 1), (1;− 1),(− 1;1), (− 1;− 1) на
7 класс 1 вариант
координатной плоскости, мишень номер 2 – это квадрат (2;2), (2;− 2), (− 2;2), (− 2;− 2), и так далее. Пуля летит по траектории y = 2|x − 2,5| + 1,5 .
Мишень с каким минимальным номером заденет эта пуля?
A) 3 B) 1 C) 5 D) 2 E) 4
9. Сколько точек, обе координаты которых целые, лежат выше графика функции y = x2 , но ниже прямой y = 7?
A) 19 B) 30 C) 29 D) 9 E) 20
10. На какой общий множитель можно сократить числитель и знаменатель записанной дроби?
y2 + 2xy − 4x − 2y 2x2 + xy + 6x + 3y
A) x + 2y B) 2x + y C) xy + 2 D) x + y + 1
E) 2xy
11. Упростите выражение:
![]() : (
: ( ![]() (0,125) a)
(0,125) a)
A) ![]() B) 5a C) 2516a
D) 2a0 E) 40
B) 5a C) 2516a
D) 2a0 E) 40
12. Разложите на множители: 1 + 4a2b2 – ( a2 + b2)2
A) (1 – a2 – b2)(1 – a2 + b2) B) (1 – a2 + b2)2
C) (1 + a2 – b2)(1 – a2 – b2) D) (1 + a2 – b2)(1 – a2 + b2)
E) другой ответ
13. Представьте в виде произведения: x2 − 2xy + x − xz + 2yz − z
A) (x − z)(x + 2y − 1) B) (x − z)(x − 2y + 1) C) (x + z)(x − 2y + 1) D) (x − y)(x − 2z + 1) E) другой ответ
14. Упростите: (2m4n3)73•(44m85n2)3 (2m n )
A) 32m19n5 B) 32m19n−5 C) 16m21n−5 D)
32m21n−7 E) другой ответ
15. Найдите наибольшее целое решение неравенства:
![]() −
− ![]() > x+21
> x+21
A) –2 B) –1 C) 1 D) 2 E) другой ответ
16. Найдите сумму целых решений неравенства
1≤|2x + 9|≤3
А) -9 B) -12 C) -14 D)-11 E) другой ответ
27. Какое число надо прибавить к многочлену 9x2 + 30x − 3 , чтобы получить квадрат двучлена?
А) 25 B) 26 C) 27 D) 28 E) другой ответ
28.
Вычислите: (![]() − 96·84) : (352 − 262)
− 96·84) : (352 − 262)
А) 16/63 B) 144/63 C) 144/61 D) 16/61 E)
другой ответ
29. В последовательности 1, 2, 3, … каждый следующий член (xn+2) вычисляется через два предыдущих (xn+1 и
xn) так:
сперва вычисляется выражение 32xn+1 − 32xn , затем оно приводится к виду обыкновенной несократимой дроби, а затем у полученного числа отбрасывается знаменатель (то есть остаётся числитель и знак числа). Например, третий член последовательности, получен так:
32·2 − 32·1 = 3 − 32 = 32→3.
Найдите седьмой член этой последовательности.
A) 35 B) 3 C) 17 D) − 27 E) 10
30. В компании 13 человек. Каждый пожал руку каждому.
Сколько рукопожатий было сделано?
A)156 B) 78 C) 13 D) 25
E) нет правильного ответа
31. Найдите количество натуральных чисел, меньших 10000, первая цифра у которых чётна.
(Ноль, как обычно, не считаем натуральным числом. Больше того, рассматриваем правильную десятичную запись числа, то есть старшая цифра не может равняться нулю)
A) 4444 B) 4000 C) 5555 D) 6500 E) 2304
32. Домик Кролика нарисован 4 раза, а домик Пятачка только один раз. Где домик Пятачка?

A B C D E
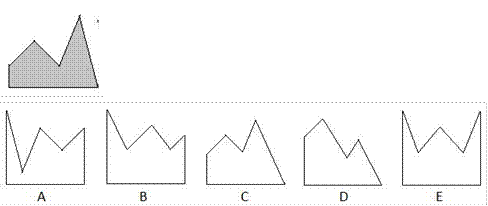
33. Какую фигуру надо добавить к закрашенной фигуре, чтобы получить квадрат?
34. Какое число должно стоять в пустующей ячейке?
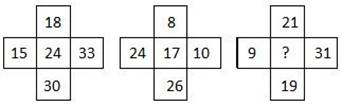
A) 24 B) 20 C) 26
D) 22 E) 25
35. Если нарисованную развертку сложить в кубик, какой из следующих кубиков получится?
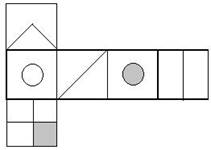
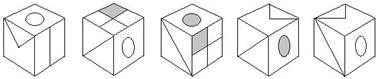
A B C D E
36. Подозрительный ювелир изготовил для королевского двора новую золотую корону. По измерениям придворного метролога объем короны составил 0,2 л, а её масса - 3,14 кг. Выясните, не обманул ли ювелир короля. Из какого металла сделана корона? Плотность золота считать равной 19,3 г/см3, железа – 7,8 г/см 3, меди – 8,9 г/см3.
(a) Чистое золото (b) Чистое железо
(c) Чистая медь (d) Сплав железа и меди
(e) Ни один из вариантов не подходит
37. Рыболов Анатолий поймал язя массой 5 кг. Под весом этой рыбы пружина его безмена растянулась на 3 см. На сколько растянется пружина этого безмена, когда Анатолий будет взвешивать на нём двухкилограммовый пакет с картошкой?
(a) 1,6 см (b) 7,5 см (c) 1,2 см (d) 3 см
(e) Ни один из вариантов не подходит
38. На идеально гладком дне морском стоит кубический обелиск неизвестного происхождения, длина ребра которого равна 0,5 м. Нижняя грань обелиска очень плотно соприкасается с поверхностью дна. Найдите выталкивающую силу, действующую на обелиск. Плотность морской воды принять равной 1030 кг/м3.
(a) 1287,5 Н (b) Выталкивающая сила не действует
(c) 1250 Н (d) 1300 Н
(e) Ни один из вариантов не подходит
39. Пупа и Лупа качаются на несимметричных качелях. Расстояние от оси качелей до Пупы составляет 2 м, при этом длина самих качелей составляет 3 м. На сколько нужно поправиться Лупе, чтобы качели пришли в равновесие, если и Пупа, и Лупа весят по 60 кг?
(a) 120 кг (b) 60 кг (c) 30 кг
(d) Поправиться нужно не Лупе, а Пупе.
(e) Ни один из вариантов не подходит
40. Полярник Геннадий в надежде поймать связь подкидывает свой телефон вертикально вверх, придавая ему скорость 8 м/c. На какую высоту поднимется телефон, если его масса составляет 130 г?
(a) 5,2 м (b) 8 м (c) 4,16 м (d) 3,2 м
(e) Ни один из вариантов не подходит
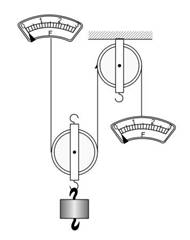
41. На рисунке ниже изображена система блоков. Определите разность показаний правого и левого динамометра, при условии, что масса грузика равна 170г.
(a) 1,7 Н (b) 3,4 Н (c) 0,85 Н (d) 0 Н
(e) Ни один из вариантов не подходит
42. На графике представлена зависимость силы натяжения пружины от её растяжения. Пользуясь графиком, определите коэффициент упругости пружины
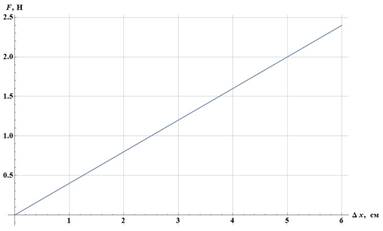
(a) 50 Н/м (b) 5 Н/м (c) 0.4 Н/м (d) 40 Н/м
(e) Ни один из вариантов не подходит
43. Первую треть пути машина ехала со скоростью 100 км/ч, вторую треть пути она ехала со скоростью 20 км/ч, третью треть - со скоростью 50 км/ч. Найдите среднюю скорость автомобиля.
(a) 20,5 км/ч (b) 57 км/ч (c) 37,5 км/ч (d) 70 км/ч
(e) Ни один из вариантов не подходит
44. Турист Евгений собирается в зимний поход. Его масса, вместе со всем снаряжением, составляет 90 кг. На каждую из своих двух ног он собирается нацепить по снегоступу. Какой минимальной площади снегоступы ему следует взять с собой в поход? Снег лежит давно, поэтому выдерживает давление 5кПа.
(a) 0,18 м2 (b) 0,018 м 2 (c) 0,55 м 2 (d) 0,30 м 2
(e) Ни один из вариантов не подходит
45. Какой площади должен быть большой поршень гидравлического пресса, чтобы на Луне весом человека можно было бы поднять БелАЗ-75710 — самый большой в мире самосвал? Масса самосвала 360 т, масса человека - 90 кг, площадь малого поршня составляет 200 м2. Ускорение свободного падения на Луне 1,6 м/с2.
(a) 0,8 км2 (b) 1,6 км 2 (c) 0,4 км 2 (d) 3,2 км 2
(e) Ни один из вариантов не подходит
46. Дед Тихомир со своими двумя внуками отправился рыбачить. Ребятишкам стало скучно и они решили сыграть в игру: кто дальше кинет грузик, а их в лодке имелось всего два массой по 1 кг каждый. Кинули дети их одновременно с одинаковой скоростью 3 м/с вдоль горизонта с неподвижной лодки. Дед узнал об этой затее только когда увидел летящие грузила, и поэтому успел поймать только один из них. Какую скорость имела лодка сразу после того, как дед поймал один из грузиков? Масса лодки со всем находящимся в ней, кроме двух грузиков, составляла 200 кг.
(a) 15 мм/с (b) 7,5 мм/с (c) 30 мм/с (d) 20 мм/с
(e) Ни один из вариантов не подходит
47. Брусок в форме параллелепипеда имеет плотность 4000 кг/м3 и геометрические размеры 5х6х7 см. Определите минимальное давление, которое может создать брусок, если поставить его на землю.
(a) 2 кПа (b) 200 Па (c) 2,8 кПа (d) 2400 Па (e) 210 Па
48. У Пети имеется электрический подъёмник с КПД η1 = 90% и генератор электричества, работающий на тепловой энергии, с КПД η2 = 40%, а также некоторое количество дров, которые дают при сжигании в печи генератора Q = 50 кДж тепловой энергии. На какую максимальную высоту Петя может поднять себя с помощью подъёмника? Масса Пети m = 60 кг.
(a) 75 м (b) 33 м (c) 30 м (d) 25 м
(e) Ни один из вариантов не подходит
49. Король Артур пытается вытянуть меч Экскалибур из камня. Считая, что сила трения в камне постоянна и равна 1000 Н, вычислите, сколько энергии затратит Артур на вытаскивание меча. Масса Экскалибура составляет 4 кг, его длина - 1 м.
(a) 1000 Дж (b) 960 Дж (c) 1040 Дж (d) 1400 Дж
(e) Ни один из вариантов не подходит
50. На яхте с бассейном отправилась в море группа из 5 друзей массой по 70 кг каждый. Масса яхты с этими людьми на борту и заполненным пресной водой бассейном составляет 4 т. Какая по величине выталкивающая сила будет действовать на яхту, когда все пятеро будут находиться в бассейне? Плотность морской воды принять равной 1030 кг/м3.
(a) 40000 Н (b) 41200 Н (c) 36500 Н (d) 37595 Н
(e) Ни один из вариантов не подходит
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.