Geometrik shakllarni proyeksiyalar tekisligiga perpendikulyar o‘q atrofida aylantirish

Geometrik shakllarni proyeksiyalar tekisligiga perpendikulyar o‘q atrofida aylantirish.

Nuqtani aylantirish. H va V tekisliklar sistemasida ixtiyoriy A nuqta va i aylanish o‘qi berilgan bo‘lsin (145 a–rasm). Agar A nuqtani i⊥V aylanish o‘qi atrofida harakatlantirsak, mazkur nuqta V tekislikka parallel V₁ tekislikda radiusi OA ga teng aylana bo‘yicha harakatlanadi. Shuningdek, A nuqtaning harakatlanish trayektoriyasining gorizontal proyeksiyasi V₁ tekislikning V_1N izi bo‘yicha harakat qiladi. Chizmada V₁ tekislik V tekislikka parallel bo‘lgani uchun A nuqtaning frontal proyeksiyasi aylana bo‘yicha, gorizontal proyeksiyasi V_1N∥Ox bo‘yicha harakat qiladi (145–rasm, b).

B nuqtaning H tekislikka perpendikulyar i o‘qi atrofida aylantirilishi 146–rasm, a da ko‘rsatilgan. B nuqta B₁ vaziyayatga radiusi OB ga teng aylana bo‘yicha H tekislikka parallel bo‘lgan N₁ tekislikda harakatlanadi. Bunda N₁ tekislik H tekislikka parallel bo‘lgani uchun B nuqta harakatlanish trayektoriyasining gorizontal proyeksiyasi aylana bo‘yicha, frontal proyeksiyasi N₁ tekislikning N_1V izi bo‘yicha Ox ga parallel bo‘lib harakatlanadi. (146,b–rasm).

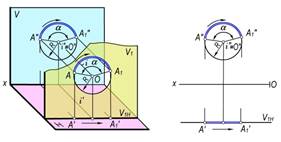
a)                         b)

145-rasm.

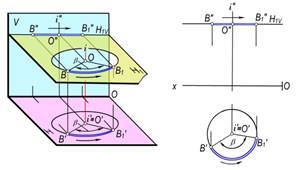
a)                                   b)

146-rasm.

Yuqorida bayon qilinganlardan quyidagi xulosalarga kelamiz:

1-xulosa. Agar A nuqta frontal proyeksiyalar tekisligiga perpendikulyar o‘q atrofida aylantirilsa, mazkur nuqtaning frontal proyeksiyasi  aylana bo‘yicha, gorizontal proyeksiyasi Ox o‘qiga parallel to‘g‘ri chiziq bo‘yicha harakatlanadi.

2-xulosa. Agar nuqta gorizontal proyeksiyalar tekisligiga perpendikulyar o‘q atrofida aylantirilsa, nuqtaning gorizontal proyeksiyasi  aylana bo‘yicha, frontal proyeksiyasi Ox o‘qiga parallel to‘g‘ri chiziq bo‘yicha harakatlanadi.

Nuqtani proyeksiyalar tekisligiga perpendikulyar o‘q atrofida aylantirish qoidalariga asosan umumiy vaziyatda joylashgan geometrik shakllarni xususiy yoki talab qilingan vaziyatga keltirish mumkin.

1–masala. Umumiy vaziyatdagi AB(A′B′, A″B″) kesmani V tekislikka parallel vaziyatga keltirilsin. (147–rasm).

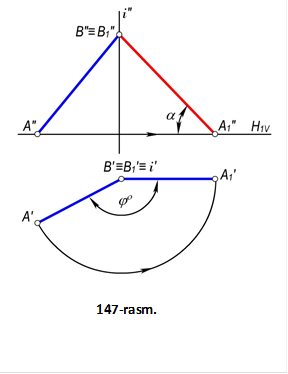Yechish. AB kesmaning biror, masalan B uchidan i⊥H aylantrish o‘qi o‘tkaziladi. So‘ngra bu o‘q atrofia kesmaning A′B′ gorizontal proyeksiyasini A′B′∥Ox vaziyatga kelguncha aylantiramiz. Bunda AB kesmaning A″ nuqtasi N_1V∥Ox bo‘yicha harakatlanib, A″₁ vaziyatni egallaydi. Shaklda hosil bo‘lgan AB kesmaning yangi A′₁B′₁ va A″₁B″₁ proyeksiyalari uning V tekislikka parallelligini ko‘rsatadi. Shakldagi α burchak AB kesmani H tekislik bilan hosil etgan burchagi bo‘ladi.

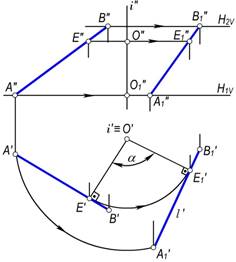
2–masala. AB(A′B′, A″B″) kesmani i⊥H o‘q atrofida α burchakka aylantirish talab qilinsin (148–rasm).

Yechish. Kesmani α burchakka aylantirish uchun uning A′ va B′ proyeksiyalarini berilgan i o‘qi atrofida A′O′₁ va B′O′₂ radiuslari bo‘yicha α burchakka aylantirish kifoya qiladi.

Aylantirish usulining qoidasiga muvofiq kesma uchlarining A″ va B″ proyeksiyalari N_1V||Ox va N_2V∥Ox bo‘yicha harakatlanadi. Natijada, hosil bo‘lgan A₁B₁(A′₁B′_1,A″₁B″₁)kesma AB kesmaning α burchakka aylantirilgan vaziyati bo‘ladi. Bu misolni quyidagicha yechish ham mumkin: AB kesmaning A′B′ gorizontal proyeksiyasiga i aylanish o‘qining gorizontal proyeksiyasi i′ dan unga perpendikulyar o‘tkaziladi. (149–rasm). Hosil bo‘lgan E′O′ aylantirish radiusni talab qilingan α burchakka aylantiriladi va E′₁O′ ga perpendikulyar qilib, l′ chiziq o‘tkaziladi. Bu chiziqqa shakldagi A′E′=A′₁E′₁ va E′B′=E′₁B′₁ kesmalar o‘lchab qo‘yiladi. So‘ngra A′₁ B′₁ ning frontal proyeksiyasi A″₁B″₁ yasaladi. Natijada AB kesmaning α burchakka aylantirilgan vaziyatining yangi A′₁B′₁ va A″₁B″₁ proyeksiyalari hosil bo‘ladi.

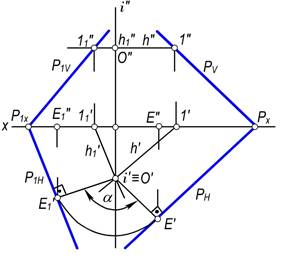
3–masala. Izlari bilan berilgan umumiy vaziyatdagi P tekislikni i⊥H o‘qi atrofida α burchakka aylantirilish talab qilinsin (150-rasm).

Yechish. P tekislikning h(h′, h″) gorizontali i aylanish o‘qi orqali o‘tkaziladi va h∩i=>O(O′,O″) aniqlanadi. So‘ngra O′ nuqtadan P_N ga O′E′ perpendikulyar tushiriladi. Hosil bo‘lgan O′E′ berilgan P tekislikni i o‘q atrofida aylantirish radiusi bo‘ladi. Tekislikning P_N gorizontal izi O′E′ radius bo‘yicha α burchakka aylantirilganda, u P_1N vaziyatni egallaydi.

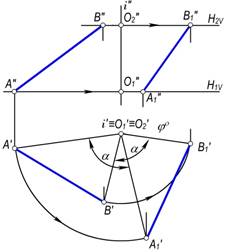
148-rasm.                                                                     149-rasm.

Tekislikning yangi P_1V frontal izini aniqlash uchun uning gorizontalidan foydalanamiz. Ma’lumki, P tekislik α burchakka aylantirilganda uning h(h′, h″) gorizontali h₁(h₁′, h₁″) vaziyatni egallaydi. Shuning uchun tekislikning P_1V izini yasashda P_1x va 1₁″ nuqtalar tutashtiriladi.

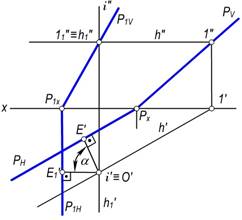
4–masala. Umumiy vaziyatdagi P(P_H,P_V) tekislikni i(i′, i″)⊥H o‘q atrofida aylantirib frontal proyeksiyalovchi tekislik vaziyatiga keltirish talab etilsin (150–shakl).

Yechish. P tekislikning h(h′,h″) gorizontali i(i′, i″) o‘qi orqali o‘tkaziladi va gorizontalning i′ o‘qi bilan kesishish nuqtasi O(O′,O″) topiladi. Tekislik bilan uning h(h′,h″) gorizontali O′ atrofida aylantirilib,  proyeksiyalovchi, ya’ni h₁′⊥Ox vaziyatga keltiriladi. Gorizontalning h″ frontal proyeksiyasi esa h₁″≡1₁″ vaziyatda bo‘ladi. Tekislikning yangi P_1V frontal izi P_1X va 1₁″ nuqtalardan o‘tadi.

150-rasm.                                                                              150-rasm.

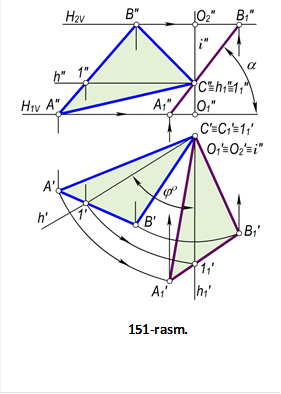5–masala. ∆ABC(∆A′B′C′, ∆A″B″C″) tekislikning H tekislik bilan tashkil etgan a burchagini aniqlansin (151–rasm).

Yechish. Izlangan α burchakni aniqlash uchun berilgan ∆ABC tekislikni frontal proyeksiyalovchi vaziyatga keltirish kerak bo‘ladi. Buning uchun uchburchakning biror, masalan, C nuqtasidan i′⊥H aylanish o‘qi o‘tkaziladi va bu o‘q atrofida uchburchakni h₁⊥V (epyurda h′₁⊥V) vaziyatga kelguncha aylantiriladi. Bunda, uchburchakning A, B va C nuqtalari ham φº burchakka harakatlanadi. Chizmada uchburchak uchlarning yangi A′₁, B′₁ va C′₁ proyeksiyalari orqali uning A″₁B″₁C″₁ frontal proyeksiyalarini aniqlanadi. Bu nuqtalar o‘zaro tutashtirilsa, A″₁B″₁C″₁ kesma (uchburchakning yangi frontal proyeksiyasi) hosil bo‘ladi. Bu kesmaning Ox o‘qi bilan tashkil etgan α burchagi ∆ABC ni H tekislik bilan hosil etgan burchagiga teng bo‘ladi.[1]

Скачано с www.znanio.ru