Гидравлический расчёт простого трубопровода. Практическая

Практическая работа № 5

Гидравлический расчет простого трубопровода

Цель работы: научиться рассчитывать линейные потери напора в трубопроводах при различных режимах течения жидкости и различной шероховатости стенок труб

Теория. В природе существует два режима течения жидкостей: ламинарный и турбулентный.

Ламинарным называется слоистое течение без перемешивания частиц жидкости и без пульсации скорости и давления.

Турбулентным называется течение, сопровождающееся интенсивным перемешиванием жидкости с пульсациями скоростей и давления

Переход от ламинарного режима к турбулентному наблюдается при определенной средней скорости движения жидкости. Эта скорость называется критической .

Значение этой скорости прямо пропорционально кинематической вязкости жидкости и обратно пропорционально диаметру трубы.

где  кинематическая вязкость;

k – безразмерный коэффициент

d – внутренний диаметр трубы

Входящий в эту формулу безразмерный коэффициент k, называется критическим числом Рейнольдса Re_кр и определяется следующим образом:

Как показывает опыт, для труб круглого сечения

Таким образом, число Рейнольдса позволяет судить о режиме течения жидкости в трубе.

При Re < Re_кр течение является ламинарным, а при Re > Re_кр течение является турбулентным. Точнее говоря, вполне развитое турбулентное течение в трубах устанавливается лишь при Re примерно равным 4000, а при Re = 2300…4000 имеет место переходная, критическая область.

Режим движения жидкости напрямую влияет на степень гидравлического сопротивления трубопроводов.

При движении реальной вязкой жидкости в трубопроводе часть энергии жидкости затрачивается на преодоление силы трения между слоями жидкости и стенками трубы, а часть – на преодоление различных препятствий в трубопроводе (вентилей, всевозможных закруглений, сужений, расширений и т.д.).

Полные потери энергии или потерянный напор  определяется

где — линейные потери, вызванные силой трения между слоями жидкости

— потери, вызванные местными сопротивлениями (изменениями конфигурации потока)

Линейные потери напора определяются формулой Дарси−Вейсбаха:

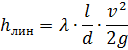
где  – коэффициент гидравлического трения; l – длина трубопровода диаметром d; v – средняя скорость потока жидкости

СИ:[] = м

Линейные потери напора δp можно выразить в единицах давления:

На практике трубопроводы делятся на короткие и длинные.

К коротким относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях.

К длинным относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы.

Учитывая гидравлическую схему работы длинных трубопроводов, их можно разделить также на простые и сложные. Простыми называются последовательно соединенные трубопроводы одного или различных сечений, не имеющих никаких ответвлений. К сложным трубопроводам относятся системы труб с одним или несколькими ответвлениями, параллельными ветвями и т.д. К сложным относятся и так называемые кольцевые трубопроводы.

Средняя скорость потока жидкости:

где  — объемный расход жидкости, м³/с

—площадь живого сечения, м²

Для круглой трубы:

Коэффициент гидравлического трения λ зависит от числа Рейнольдса и от относительной шероховатости стенок трубы δ/d

Где δ – эквивалентная шероховатость стенок трубопровода, дается в таблице

Характерные значения δ (в мм) для труб из различных материалов приведены ниже:

При ламинарном течении коэффициент гидравлического трения λ зависит от числа Рейнольдса Re и не зависит от относительной шероховатости и вычисляется по выражению:

При турбулентном движении в гидравлически гладких трубах в диапазоне чисел Рейнольдса 4000 < Re < 10d/δ коэффициент λ определяется по формуле Блазиуса:

Для круглых труб различной шероховатости в диапазоне чисел Рейнольдса             10d/δ < Re < 560d/δ коэффициент λ зависит одновременно от двух параметров – числа Re и относительной шероховатости δ/d.

Для определения коэффициента λ в этой области может служить универсальная формула А.Д. Альтшуля:

Где δ – эквивалентная абсолютная шероховатость.

При больших Re > 560 δ/d, коэффициент λ не зависит от числа Re, а определяется лишь относительной шероховатостью. Определение λ для этой области производят по упрощенной формуле Альтшуля:

Исходные данные для расчетов

В качестве исходных данных задаются:

- два вида жидкостей: вода и нефть;

- плотность воды ; плотность нефти ;

- динамическая вязкость воды ; динамическая вязкость нефти          ;

- длина трубопровода l

- диаметр трубопровода d;

- объемный расход Q;

- относительная шероховатость трубы δ/d

Исходные данные представлены в таблице.

Порядок проведения расчетов

1.                 Зная диаметр трубопровода, найти площадь живого сечения.

2.                 Зная объемный расход и площадь живого сечения найти среднюю скорость потомка.

3.                 По заданным параметрам жидкости, известным диаметру трубопровода и средней скорости найти число Рейнольдса.

4.                 Зная число Рейнольдса и относительную шероховатость, определить соответствующий частный случая для расчета коэффициента гидравлического трения λ и найти его значения.

5.                 Рассчитать линейные потери напора, выраженные в единицах длины и в единицах давления.

Результаты расчетов

Исходные и полученные данные для каждой жидкости (воды и нефть) занести в таблицу.