
Графическое описание логической функции
![]()
![]() Графическое представление чаще всего применяется для
описания схемы устройства, которое
реализует заданную функцию. Логические функции
в этом случае называют переключательными функциями. Рас- смотрим основные переключательные функции
и их условные графиче- ские обозначения.
Графическое представление чаще всего применяется для
описания схемы устройства, которое
реализует заданную функцию. Логические функции
в этом случае называют переключательными функциями. Рас- смотрим основные переключательные функции
и их условные графиче- ские обозначения.
![]()
![]() Y =`x (НЕ) x
Y =`x (НЕ) x
Y x
Y Функция инверсии.
![]()
Y = x1 + x2
![]()
![]() са.
са.
(ИЛИ-НЕ)
x1
![]()
Y Функцию ИЛИ-НЕ иногда называют стрелкой Пир-
![]()
![]() Y = x1 · x2
Y = x1 · x2
(И-НЕ)
x2 Функция определена для любого числа аргументов.
![]()
![]() x1 Y Функцию И-НЕ иногда называют
стрелкой Пирса.
x1 Y Функцию И-НЕ иногда называют
стрелкой Пирса.
![]()
![]() x2 Функция определена для любого числа аргументов.
x2 Функция определена для любого числа аргументов.
Набор функций, из которого методом суперпозиции можно получить лю- бую переключательную функцию, называется логически (функциональ- но) полным. Функционально полный набор образуют логическое сложе- ние, умножение и инверсия. Причем сложение по закону де Моргана можно заменить умножением с инверсией аргументов. Аналогично умно- жение можно заменить сложением с инверсией аргументов. Таким обра- зом, каждая из функций ИЛИ-НЕ и И-НЕ является функционально пол- ной.
В ЭВМ широко используются функции двух переменных для проверки их равнозначности или неравнозначности.Формально они не относятся к основным, так как их можно реализовать на базе рассмотренных выше функций. Но ввиду распространенности на практике эти функции часто относят к основным функциям. Рассмотрим условные обозначения и ло- гику этих функций.
![]() Y = x1Åx2 =
Y = x1Åx2 =
![]()
![]()
x2 x1 + x1 x 2
(М2). Функция неравнозначности. Используется
![]() для
арифметического сложения аргументов по модулю 2 и проверки пере- менных на несовпадение их значений.
для
арифметического сложения аргументов по модулю 2 и проверки пере- менных на несовпадение их значений.
Y = x1Åx2 (= =) . Функция равнозначности. Используется для проверки переменных на совпадения их значений. Эта функция представляет собой инверсию функции неравнозначности.
![]()
![]() Таблица истинности функции Таблица истинности функции неравнозначности (М2) равнозначности M 2
Таблица истинности функции Таблица истинности функции неравнозначности (М2) равнозначности M 2
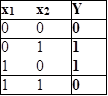
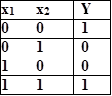
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.