МНОГОПРОФИЛЬНЫЙ ТЕХНОЛОГИЧЕСКИЙ КОЛЛЕДЖ ФГБОУ ВО   «ДОНБАССКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

УТВЕРЖДАЮ

Заместитель директора по УМР, председатель методического совета ______________ Л.Л. Кузьмина «_____» ____________ 2025 г.

МЕТОДИЧЕСКАЯ РАЗРАБОТКА 

открытого занятия 

по дисциплине «Элементы высшей математики» 

на тему: «Решение систем линейных уравнений»

г. Алчевск

2025

Разработчик____________ О.Н.Максимова, преподаватель первой категории

Согласовано ___________ С.И. Васильченко, методист

Рассмотрено и одобрено к использованию в образовательной  деятельности на заседании методической комиссии  естественнонаучных дисциплин 

Протокол №______  от «____»__________ 2025 года Председатель комиссии ____________ О.А. Гиркина Тема занятия: «Решение систем линейных уравнений».

Вид занятия:  лекция.

Цели занятия:

Обучающие:  показать применение определителей, метода Гаусса и закрепить умения и навыки математического моделирования при решении задач, характерных для будущей профессиональной деятельности.

Воспитательные:  

продолжить формирование необходимости повышения профессионального уровня; продолжить формирование умения принимать решения и отвечать за принятые решения.

Развивающие:  

продолжить отрабатывать вычислительные навыки при решении задач по специальности; продолжить развитие умений обобщать, систематизировать, делать выводы, сравнивать. Методы:

Беседа, Решение задач у доски и в тетрадях. Решение    студентом    у    доски  с полным объяснением.

Наглядность и оборудование: Опорные конспекты, раздаточный материал.

План урока:

1.  Организационный момент – 5 мин.

2.  Мотивация к учебной деятельности – 5 мин.

3.  Беседа по теме занятия – 45 мин.

4.  Закрепление нового материала – 20 мин.

5.  Подведение итогов – 5 мин.

Ход урока

«Приобретение любого познания всегда полезно для ума, ибо оно сможет бесполезное, и сохранить хорошее. Ведь ни одну вещь нельзя, ни любить, ни ненавидеть, если сначала ее не познать».

Леонардо да Винчи   

I. Организационный момент

Преподаватель приветствует студентов, отметка в журнале отсутствующих студентов, объявление темы. Привлекает студентов в определение целями и структурой урока.

II. Мотивация к учебной деятельности

Преподаватель мотивирует студентов на приобретение навыков построения простых разрезов (фронтального, профильного, горизонтального) и их обозначение, а так же местных разрезов, что в дальнейшем будет способствовать свободному и быстрому выполнению заданий.

III. Беседа по теме занятия

Преподаватель знакомит студентов с новым теоретическим материалом. 

Мы познакомились на уроках с различными методами решения систем линейных уравнений. Перечислите их: (студенты перечисляют следующие методы)

Метод Крамера;

Метод обратной матрицы (матричный метод);

Метод Гаусса.

Теперь я предлагаю задачи с экономическим содержанием, которые можно решить, используя ваши теоретические знания по математике.

Предлагаю рассмотреть задачу, характерную для Вашей специальности, при выполнении которой составим и решим систему линейных алгебраических уравнений (с использованием определителя II порядка).

Рассмотрим задачу 1.

(Студент решает у доски, остальные самостоятельно в тетрадях) Условие:

Для пошива униформы в Торговый Дом «Сибвез» было закуплено 5м. ткани одного вида и 5м. ткани другого вида. Стоимость покупки составила 300 денежных единиц. Найти стоимость 1м. каждой ткани, если 4м. одной ткани стоит столько же, сколько 6 м. другой.

Решение:

Конечно, решение этой задачи не составит труда, т.к. за х - обозначим стоимость 1м. ткани одного вида, за у - стоимость одного метра ткани другого вида. В соответствии с условием задачи составив два уравнения:

5х+5у = 300  и  4х = 6у   

Так как записанные условия выполняются одновременно, то составим и решим систему:  

Решение  этой системы вы можете выполнять методом подстановки, т.е. когда одна неизвестная выражается через другую и это значение неизвестной подставляется в подстановку, находится вторая переменная. Эту же систему можно решить способом сложения или графически.

Предлагаю вам вспомнить все эти методы и проверить себя.

                                   ↔       ↔ 

(36;24) т.е. стоимость одного метра ткани другого вида-24 ден.ед.

На этом примере рассмотрим новый метод: метод Крамера:

далее найдем главный и вспомогательные определители системы:

∆==-30-20=-50

=-1800-0=-1800

у ==0-1200=-1200

                                   Х= = =36,           у = =  =24

(36,24)

Рассмотрим задачу 2.

Преподаватель: Рассмотрим задачу, характерную для вашей специальности, при выполнении которой составим и решим систему линейных алгебраических уравнений (с использованием определителей III порядка).

Условие:

Торговая фирма закупила в прошлом году: компьютеры, принтеры и сканеры на сумму 10 млн. ден.ед. В результате реализации была получена прибыль 780 тыс. ден.ед. В текущем году эта фирма планирует увеличить товарооборот, поэтому сумма, затраченная на приобретение компьютеров, была увеличена в 2 раза, принтеров - в 3 раза, а денежная сумма, затраченная на приобретение сканеров, оставлена на прошлогоднем уровне. На все это выделено 22 млн. ден.ед. какую прибыль планирует получить торговая фирма в текущем году, если реализация компьютеров приносит 10% прибыли на вложенные средства, принтеров - 8% и сканеров - 6%.

Решение:

Задачу на доске решает преподаватель с привлечением студентов.

Для решения задачи введем обозначения:

х - сумма денег (млн.ден.ед), затраченная на приобретение

компьютеров, у - принтеров,

z- сканеров.

По условию задачи: 

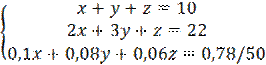
Сделаем преобразования: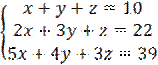  

Вычислим определители:

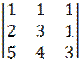∆==9+8+5-15-4-6=-3≠0

∆х=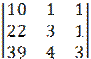=90+88+39-117-40-66=-6

у=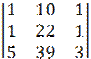=66+78+50-110-39-60=-15

∆z=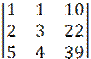=117+80+110-150-88-78=-9

Далее по формуле Крамера:  Х==2; У==5; Z==3/ (студенты вычисляют определитель любым способом).

Преподаватель делает акцент на то, что найдены значения всех переменных в задаче, но нет ответа на поставленный вопрос. Для этого необходимо определить, какие суммы денег затрачены на приобретение компьютеров, принтеров, сканеров в текущем году. Для компьютеров эта сумма составит: 2х = 2 ∙ 2 = 4 млн.ден.ед.

принтеров - Зу = 3 ∙ 5 = 15 млн.ден.ед.

сканеров- z= 3 млн.ден.ед.

Найдем общую прибыль, ожидаемую в текущем году: П = 4 ∙|о,1 + 15 ∙ 0,08 + 3 ∙ 0,06 = 1,78 млн.ден.ед.

При выполнении данной задачи актуализируется понятие «прибыль на вложенный капитал» - доходы от вложений как доля этих вложений.

Рассмотрим задачу 3.

Условие:

У завода есть четыре потребителя, которым ежедневно отгружается готовая продукция. Груз доставляется каждому потребителю упакованным в ящики, маркированные в зависимости от вида продукции, на автомашине. Однажды, когда автомашины были уже отправлены, но еще находились в пути, обнаружилось, что один из 4 видов груза был отправлен по ошибке и его следует возвратить (причем в полной сохранности и без нарушения целостности остальных грузов). Одновременно выяснилось также, что по недосмотру служащего не осталось никаких сведений о том, как именно маркирована та партия ящиков, в которой находился этот подлежащий возврату груз. А что же известно? Известно количество маркированных ящиков каждого вида, общий вес груза в каждой машине, (таблица):

а также и то, что ящики с возвращаемым грузом должны быть тяжелее остальных. Возникает вопросу нельзя ли дать рекомендации по изъятию этого груза без распаковки и дополнительного взвешивания.

Решение: (преподаватель объясняет, как записать систему)

Оказывается можно. Приведем расчеты при помощи,  которых совсем не трудно выйти из ситуации.

Обозначим через Хк вес ящика с R-ым видом груза. Тогда общий вес груза на автомашине можно подсчитать так:

Х1+4х2+9х3+8х4=51

Аналогично составим уравнения для всех остальных машин и запишем получившееся уравнения системой:

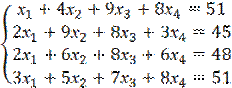
 Решим эту систему методом Гаусса.  Запишем расширенную матрицу: (решает студент у доски с полным объяснением, опережающее обучение)

↔

↔

В результате решения системы получили, что х1=1, х2=2, х3=2, х4=3. Отсюда вытекает, что нужно вернуть на завод ящики с 4 видом груза , т.е

8+3+6+8=25 ящиков.

IV. Закрепление нового материала

Преподаватель осуществляет контроль над работой студентов во время проведения занятия, следит за конспектированием лекционного материала. Студенты группы получают практические навыки по предстоящей работе, при необходимости обращаются за разъяснениями к преподавателю.

V. Подведение итогов занятия

Преподаватель анализирует и оценивает работу студентов и обобщает их знания и умения.

В тетрадях каждого студента предлагается письменно ответить на вопросы:

1.  На уроке я работал активно / пассивно;

2.  Своей работой на уроке я доволен / не доволен;

3.  Материал урока мне был понятен / не понятен, полезен /

бесполезен, интересен / скучен;

4.  Наиболее трудным было при решении задач:

5.  Я научился:

6.  Я оцениваю свою деятельность на 5 / 4 / 3 балла.

Таким образом, подводя итоги нашего урока можно сказать, что математический аппарат, который был изучен на лекционных занятиях, был востребован в процессе решения профессионально ориентированных математических задач.

Заключение

Данная методика  проведения урока - закрепление теоретических знаний, помогает реализовать поставленные цели и задачи:

-                прививать положительное отношение к знаниям; 

-                развивать контроль и самоконтроль;

-                отрабатывать  вычислительные  навыки  при  решении  систем линейных  уравнений;

-                закреплять способы вычисления систем линейных уравнений методами  Крамера, Гаусса;

-                активировать умственную деятельность студентов на протяжении всего  урока; 

-                прививать интерес к дисциплине и выбранной профессии;

-                пополнять словарный запас.

Список литературы.

1.        Богомолов   Н.В.   Практические  занятия   по   высшей   математике.  Учебное пособие для техникумов. М., «Высшая школа», 1973 - 472с.

2.        Глейзер Г.И. История математики в средней школе. Пособие для учителей. М., Просвещение, 1970.

3.        Письменный Д.Г. Конспект лекций по высшей математике. 1 часть. - М.: Айрис-пресс, 2002 - 288с.

4.        Подольский В.А., Суходский А.М. Сборник задач по высшей математике. -М.: 1974 -349с.

5.        Шипачев В.С. Задачник по высшей математике: Учебное пособие для ВУЗов. - М.: «Высшая школа», 1998 - 304с.