План -конспект урока по теме: "Матрицы"

Министерство образования и молодежной политики Чувашской Республики

Государственное автономное профессиональное

образовательное учреждение Чувашской Республики

«Чебоксарский техникум транспортных и строительных технологий»

Методическая разработка занятия по дисциплине

ЕН.01Математика

На тему: «Матрицы»

Разработала:

преподаватель математики

Андреева Н.А.

Чебоксары 2020

Содержание

Пояснительная записка                                                                            3

Дидактическая структура урока                                                              4

Учебно-методическая карта урока                                                          5

Ход урока                                                                                                6

Пояснительная записка

Методическая разработка учебного занятия по дисциплине ЕН.01 Математика на тему «Матрицы» с применением основных методов обучения: словесный, наглядный, частично-поисковый, наглядно-иллюстративный.

Цель изучения данной темы: Сформировать навыки выполнения операций над матрицами, вычисления определителя матрицы, развивать логическое мышление и воображение, воспитывать активность, самостоятельность, интерес к предмету.

Описание материала: данная методическая разработка предназначена для изучения темы «Матрицы» студентами средних специальных заведений, материал будет полезен преподавателям математики в средних специальных учебных заведений. Урок построен с применением методов репродуктивного и частично-поискового обучения.

Дидактическая структура урока

Цель урока: Сформировать навыки выполнения операций над матрицами, вычисления определителя матрицы.

Задачи урока:

Образовательные – ознакомиться с понятиями матрицы, определителя матрицы, научиться выполнять действия над матрицами.

Воспитательные - воспитывать умение применять теоретические знания на практике, внимательность, самостоятельность.

Развивающие – развивать коммуникативные навыки во время практической работы, организовывать собственную деятельность.

Тип урока: урок усвоения новых знаний.

Методы обучения: словесный, наглядный, частично-поисковый, наглядно-иллюстративный.

Формы обучения: фронтальная, индивидуальная.

Планируемые образовательные результаты.

Студент должен знать:

·         понятие матрицы и ее элементы;

·         основные виды матриц;

·         свойства операций над матрицами;

·         виды определителей и их свойства.

Студент должен уметь:

·         определять вид матрицы

·         выполнять операции с матрицами (сложение, вычитание матриц, умножение матрицы на число, умножение матрицы на матрицу).

·         вычислять определитель матрицы.

Оборудование: учебник «Математика» под редакцией Е.В. Филимонова, «Сборник задач по математике с решениями для техникумов» под ред. И.Л. Соловейчик, презентация, компьютер, проектор, экран.

Учебно-методическая карта урока

Ход урока:

1. Организационный этап.

Приветствие студентов. Проверка наличия студентов в аудитории.

2. Постановка цели урока. Мотивация учебной деятельности учащихся.

Цель занятия - изучение теоретического материала и формирование практических навыков при решении задач по теме: «Матрицы. Операции с матрицами. Определитель".

Матричная алгебра широко применяется в различных отраслях знания – в математике, физике, информатике, экономике, электронике. Например, матрицы используется для решения систем алгебраических и дифференциальных уравнений, нахождения значений физических величин в квантовой теории, шифрования сообщений в Интернете.

Впервые матрицы упоминались ещё в древнем Китае, называясь тогда «волшебным квадратом». Основным применением матриц было решение линейных уравнений. 

При решении систем линейных уравнений используют такие методы как: Метод Гаусса, Метод Крамера, Матричный метод. Данные методы связаны с понятием матрицы и определителя матрицы.

3. Первичное усвоение новых знаний.

Определение матрицы. Виды матриц.

Матрица – таблица прямоугольной формы, заполненная числами или символами их обозначающими.

Матрица записывается в виде:

1)

Матрица состоит из m строк и n столбцов Числа и символы называются элементами матрицы. , расположенных в одной строке называют строкой матрицы; Множество элементов матрицы , расположенных с одном столбце - столбцом матрицы.

2) А

где i – номер строки i = 1, 2, 3..., m;

j – номер столбца j = 1, 2, 3..., n;

m – количество строк;

n – количество столбцов.

Матрицу А называют матрицей размера m×n (

Пример 1.

Дана матрица A размера 3×4.

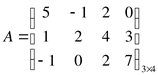
Матрица A состоит из трех строк и четырех столбцов. Элемент матрицы 5, = - 1, =7.

Виды матриц:

1.     Матрицу называют квадратной, если количество ее строк и столбцов совпадают (m=n).

Матрица n-го порядка – квадратная матрица размера n×n.

Пример 2.

Матриц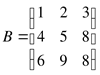а  - квадратная матрица третьего порядка.

2.     Матрица строка – матрица размера 1×n, состоящая из одной строки.

3.     Матрица столбец – матрица размера m×1, состоящая из одного столбца.

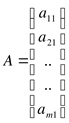
4.     Диагональная матрица – квадратная матрица, все элементы которой, кроме элементов главной диагонали, равны дулю.

5.     Нулевая матрица – матрица, все элементы которой равны нулю.

6.     Единичная матрица – диагональная матрица, элементы главной диагонали которой равны единице.

7.     Треугольная матрица - квадратная матрица, все элементы которой, расположенные по одну сторону от главной диагонали, равны нулю.

8.     Матрица называется транспонированной, если в матрице заменить строки соответствующими столбцами. (Обозначение - A^T)

; 

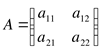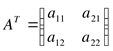
Операции над матрицами.

Сложение матриц

Операция сложения матриц вводится для матриц одинакового размера. При сложении матриц складываются соответствующие элементы.

Пример 4.

, 

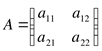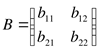
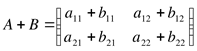
Свойства операции сложения матриц:

1.     A+B=B+C

2.     A+(В+С) =(А+В) +С.

3.     А+О=А.

Вычитание матриц

Операция вычитания матриц производится аналогично сложению.

Пример 5.

Найти сумму и разность матриц  и 

Умножение матриц на число.

При умножении матрицы на число каждый элемент матрицы умножается на это число.

Пример 6.

, 

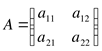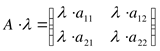
Произведение матриц

Операция умножения двух матриц вводится только для случая, когда число столбцов первой матрицы равно числу строк второй матрицы.

Произведением двух матриц  на матрицу  называется матрица такая, что  где  элемент i-й строки и k-го столбца матрицы произведения С равен сумме произведений элементов i-й строки матрицы А на соответствующие элементы k-го столбца матрицы В.

Свойства операции умножения матриц:

1.    

2.    

Пример 6.

Найти произведение двух матриц  A=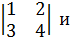 B=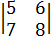

Пример 7.

Даны две матрицы:

, 

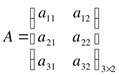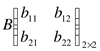
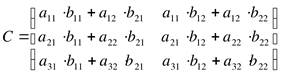
Определитель матрицы

Вычисление определителя второго порядка

Дана 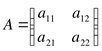 квадратная матрицы второго порядка.

Определителем второго порядка матрицы A называется число

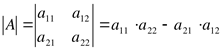
Из произведения элементов главной диагонали вычитаем произведение элементов побочной диагонали.

Пример 8.

Вычислить определитель второго порядка.

Вычисление определитель третьего порядка (метод треугольников)

Дана 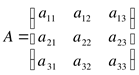 квадратная матрицы третьего порядка

Определителем третьего порядка матрицы А называется число

 Для начала перемножаем элементы главной диагонали и описываем два треугольника вокруг диагонали следующим образом:

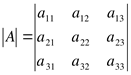
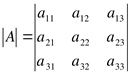
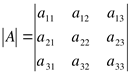
Элементы, стоящие на вершинах треугольника, перемножаем.

Затем ставим минус, перемножаем элементы побочной диагонали и описываем два треугольника вокруг побочной диагонали:

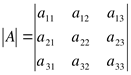
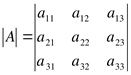
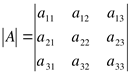
Пример 9.

Вычислить определитель третьего порядка методом треугольников.

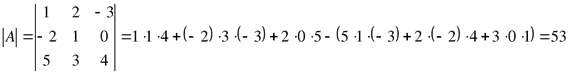
Разложение определителя по элементам какой-либо строки или столбца.

Минором  какого либо элемента определителя А называется определитель, полученный из данного путем вычеркивания строки и столбца на пересечении которого находится этот элемент.

Алгебраическим дополнением элемента определителя А называется его минор, взятый со знаком 

Определитель равен сумме произведений элементов какой-либо строки или столбца на их алгебраическое дополнение.

- разложение определителя по элементам строки.

- разложение определителя по элементам столбца.

Пример 10.

Дана матрица A. Найти минор  и алгебраическое дополнение .

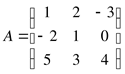
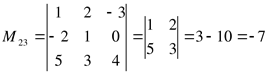
Свойства определителей

- величина определителя не меняется, если заменить его строки соответствующими столбцами;

- определитель не меняется, если к элементам какой-либо строки прибавить соответствующие элементы другой строки, умноженные на одно и тоже число (то же самое и для столбца);

- определитель меняет знак, если поменять местами строки или столбцы;

- общий множитель строк или столбцов можно вынести за знак определителя;

- определитель равен нулю, если все элементы какого-либо столбца или строки равны нулю;

- определитель равен нулю, если элементы двух строк или столбцов соответственно равны.

4. Первичная проверка понимания.

Студенты выходят к доске и с помощью преподавателя решают задания.

Пример 11. Дана матрица  и . Найти: 

Решение:

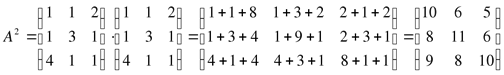
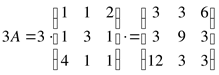
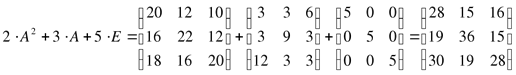
Пример 12: Вычислить определитель второго порядка.

Пример 13: Вычислить определитель третьего порядка методом треугольника

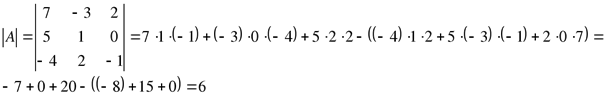
Пример 14: Вычислить определитель разложением по элементам, какой-либо строки или столбца.

Воспользуемся свойствами определителя и обнулим все элементы, стоящие в первом столбце кроме первого. Для этого: каждый элемент первой строки умножим на 2 и прибавим к ним соответствующий элемент второй строки; каждый элемент первой строки умножим на (-5) и прибавим к ним соответствующие элементы третьей строки.

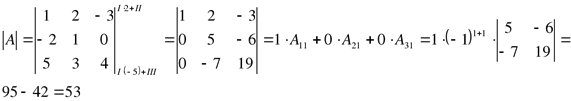
Пример 15: Вычислить определитель четвертого порядка.

5. Первичное закрепление.

Студентам предлагается самостоятельно на оценку выполнить следующие задания:

1. Даны матрицы ,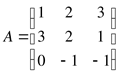 

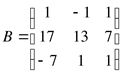
Найти: 

2. Дана матрица 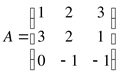. Вычислить определитель матрицы.

3. Вычислить определитель 

6. Информация о домашнем задании, инструктаж по его выполнению.

1. Выучить теоретический материал;

2. Выполнить действия над матрицами

, , 

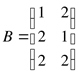3. Вычислить определитель матрицы третьего порядка

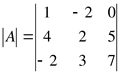
4. Вычислить определитель матрицы четвертого порядка

7. Задание ученикам по рефлексии их деятельности.

Итак, сегодня мы с вами изучили тему: «Матрица и определитель». Давайте повторим основные понятия данной темы: матрица, виды матриц, определитель, минор, алгебраическое дополнение. Какие действия мы можем выполнять с матрицей? (сложение, вычитание, умножение на число, перемножения матриц).

Также мы научились: вычислять определитель второго порядка, третьего порядка методом треугольников, применять метод вычисления определителя с помощью разложения по элементам строки и столбца.

Список использованной литературы

1.      Григорьев В.П. Математика: учебник для студ. учреждений сред. проф. образования – М.: «Академия», 2017

2.      Григорьев В.П.  Сборник задач по высшей математике: учеб. пособие для студ. учреждений сред. проф. образования – М.: «Академия», 2017

3.      Элементы высшей математики: учеб. для студ. учреждений сред. проф. образования / В.П.Григорьев, Ю.А.Дубинский, Т.Н.Сабурова. -М.: «Академия», 2016

4.      Сборник задач по математике для техникумов / И.Л.Соловечик, В.Т. Лисичкин.- М.: «ОНИКС 21 век», 2003