Характеристики центра розподілу

Характеристики центра розподілу

Центром тяжіння будь-якої статистичної сукупності є типовий рівень ознаки, узагальнююча характеристика всього розмаїття її індивідуальних значень. Такою характеристикою є середня величина . За даними ряду розподілу середня обчислюється як ариф­метична зважена; вагами є частоти f_j або частки d_j:

,    ,

де j — номер групи; m — число груп.

В інтервальних рядах, припускаючи рівномірний розподіл елементів сукупності в межах j-го інтервалу, як варіанту  використовують середину інтервалу. При цьому ширину відкритого інтервалу умовно вважають такою самою, як сусіднього закритого інтервалу.

Дані для розрахунку середнього рівня в інтервальному ряду розподілу наведено в табл. 5.4. Згідно з розрахунками, у середньому на одного члена домогосподарства припадає  = 1800 : 200 = 9 м² житлової площі. Це типовий рівень забезпеченості населення житлом.

РОЗПОДІЛ ДОМОГОСПОДАРСТВ МІСТА ЗА РІВНЕМ
ЗАБЕЗПЕЧЕНОСТІ ЖИТЛОМ

Окрім типового рівня важливе значення має домінанта, тобто найбільш поширене значення ознаки. Таке значення називають модою (Мо). У дискретному ряду моду визначають безпосередньо за найбільшою частотою (часткою). Наприклад, якщо депозитна ставка у восьми комерційних банків — 12% річних, а в двох — 10%, то модальною є ставка 12%.

В інтервальному ряду за тим самим принципом визначається модальний інтервал, а в разі потреби конкретне модальне значення в середині інтервалу обчислюється за інтерполяційною формулою

,

де  та h — відповідно нижня межа та ширина модального інтервалу, , ,  — частоти (частки) відповідно модального, передмодального та післямодального інтервалів.

За даними табл. 5.4 модальним є інтервал 7 — 9, що має найбільшу частоту ; ширина модального інтервалу h = 2; нижня межа х₀ = 7; передмодальна частота = 39, післямодальна — = 42. За такого співвідношення частот модальне значення забезпеченості населення житлом:

= 8,1 м².

Для моди як домінанти число відхилень (х – Мо) мінімальне. Оскільки мода не залежить від крайніх значень ознаки, то її доцільно використовувати тоді, коли ряд розподілу має невизначені межі.

Характеристикою центра розподілу вважається також медіана (Ме) — значення ознаки, яке припадає на середину впорядкованого ряду, поділяє його навпіл — на дві рівні за обсягом частини. Визначаючи медіану, використовують кумулятивні частоти  або частки . У дискретному ряду медіаною буде значення ознаки, кумулятивна частота якого перевищує половину обсягу сукупності, тобто  (для кумулятивної частки ).

В інтервальному ряду за цим принципом визначають медіанний інтервал, а значення медіани в середині інтервалу, як і значення моди, обчислюють за інтерполяційною формулою:

,

де x₀ та h — відповідно нижня межа та ширина медіанного інтервалу; f_me — частота медіанного інтервалу;  — кумулятивна частота передмедіанного інтервалу.

За даними табл. 5.4 половина обсягу сукупності  припадає на інтервал 7 — 9 з частотою = 51; передмедіанна кумулятивна частота = 56. Отже, медіана забезпеченості населення житлом:

м².

У симетричному розподілі всі три зазначені характеристики центра розподілу однакові: , у помірно асиметричному відстань медіани до середньої втричі менша за відстань середньої до моди, тобто . Саме таке співвідношення характеристик центра розподілу в розглянутому прикладі:

3 (9 – 8,7) = 9 – 8,1.

Медіана, як і мода, не залежить від крайніх значень ознаки; сума модулів відхилень варіант від медіани мінімальна, тобто вона має властивість лінійного мінімуму:

.

Цю властивість медіани можна використати при проектуванні розміщення зупинок міського транспорту, заготівельних пунктів тощо.

Окрім моди і медіани, в аналізі закономірностей розподілу використовуються також квартилі та децилі. Квартилі — це варіанти, які поділяють обсяги сукупності на чотири рівні частини, децилі — на десять рівних частин. Ці характеристики визначаються на основі кумулятивних частот (часток) за аналогією з медіаною, яка є другим квартилем або п’ятим децилем.

У ряду розподілу (див. табл. 5.4) перший квартиль становить 6,7 м², перший дециль — 5,2 м², дев’ятий — 13,3 м² :

;

;

.

Отже, у 25% сімей забезпеченість житлом не перевищує 6,7 м², серед 10% малозабезпечених найвищий рівень становить 5,2 м², а серед 10% найбільш забезпечених нижня межа — 13,3 м².

В одних сукупностях індивідуальні значення ознаки щільно групуються навколо центра розподілу, в інших — значно відхиляються. Чим менші відхилення, тим однорідніша сукупність, а отже, тим більш надійні й типові характеристики центра розподілу, передусім середня величина. Вимірювання ступеня коливання ознаки, її варіації — невід’ємна складова аналізу закономірностей розподілу. Міри варіації широко використовуються у практичній діяльності: для оцінювання диференціації домашніх господарств за рівнем доходу, фінансового ризику інвестування, ритмічності роботи підприємств, сталості врожайності сільськогосподарських культур тощо.

На основі характеристик варіації оцінюється інтенсивність структурних зрушень, щільність взаємозв’язків соціально-еконо­мічних явищ, точність результатів вибіркового обстеження.

Для вимірювання та оцінювання варіації використовуються абсолютні та відносні характеристики. До абсолютних належать: варіаційний розмах, середнє лінійне та середнє квадратичне відхилення, дисперсії; відносні характеристики подаються низкою коефіцієнтів варіації, локалізації, концентрації.

Варіаційний розмах R — це різниця між максимальним і мінімальним значеннями ознаки: R = x_max – x_min. Він характеризує діапазон варіації, наприклад родючості ґрунтів у регіоні, продуктив­ності праці в галузях промисловості тощо. Безперечною перевагою варіаційного розмаху як міри варіації є простота його обчислення й тлумачення.

Проте, коли частоти крайніх варіант надто малі, варіаційний розмах неадекватно характеризує варіацію. У таких випадках використовують квартильні або децильні розмахи. Квартильний розмах  охоплює 50% обсягу сукупності, децильний  — 60%  або   — 80%.

Інші абсолютні характеристики варіації враховують усі відхилення значень ознаки від центра розподілу, поданого середньою величиною. Оскільки алгебраїчна сума відхилень , то використовуються або модулі відхилень , або квадрати відхилень . Узагальнюючою характеристикою варіації є середнє відхилення:

а) лінійне

;

б) квадратичне, або стандартне

;

в) дисперсія (середній квадрат відхилень)

.

На підставі первинних, незгрупованих даних наведені характеристики обчислюють за принципом незваженої середньої:

   або   .

Середнє лінійне  та середнє квадратичне  відхилення є безпосередніми мірами варіації. Це іменовані числа (в одиницях вимірювання ознаки), за змістом вони ідентичні, проте завдяки математичним властивостям . Коли обсяг сукупності досить великий і розподіл ознаки, що варіює, наближається до нормального, то , а . Значення ознаки в межах  мають 68,3% обсягу сукупності, у межах  — 95,4%, у межах  — 99,7%. Це відоме «правило трьох сигм». При значній асиметрії розподілу (див. підрозд. 5.4) розрахунок  не має сенсу.

На основі взаємозв’язку між варіаційним розмахом R, середнім квадратичним відхиленням  і чисельністю сукупності n Р. Пірсон обчислив коефіцієнти k, за допомогою яких орієнтовно можна визначити середнє квадратичне відхилення за варіаційним розмахом: . Значення коефіцієнтів k наведено в табл. 5.5.

КОЕФІЦІЄНТИ k ДЛЯ РІЗНОГО ОБСЯГУ СУКУПНОСТІ

Очевидний взаємозв’язок середнього квадратичного відхилення та дисперсії: . Дисперсія входить до більшості теорем теорії ймовірностей, які є фундаментом математичної статистики, і широко використовується для вимірювання зв’язку й перевірки статистичних гіпотез. Види та властивості дисперсій розглядаються в підрозд. 5.5.

При порівнянні варіації різних ознак або однієї ознаки в різних сукупностях використовуються коефіцієнти варіації V. Вони визначаються відношенням абсолютних іменованих характеристик варіації (, , R) до центра розподілу, найчастіше виражаються у процентах. Значення цих коефіцієнтів залежить від того, яка саме абсолютна характеристика варіації використовується. Отже, маємо коефіцієнти варіації:

лінійний                 ;

квадратичний       ;

осциляції               .

Якщо центр розподілу поданий медіаною, то за відносну міру варіації беруть квартильний коефіцієнт варіації

.

Для оцінювання ступеня варіації застосовують також співвідношення децилів. Так, коефіцієнт децильної диференціації показує кратність співвідношення дев’ятого та першого децилів:

.

Необхідні для розрахунку узагальнюючих характеристик варіації величини подано в табл. 5.6 на прикладі розподілу домогосподарств за рівнем забезпеченості житлом. Середня розподілу становить 9 м².

ДО РОЗРАХУНКУ УЗАГАЛЬНЮЮЧИХ ХАРАКТЕРИСТИК ВАРІАЦІЇ

Згідно з розрахунками:

2,53 м²;

;

м²;

.

Децильний коефіцієнт V_D = 13,3 : 5,2 = 2,5 показує, що нижня межа 10% відносно забезпечених житлом домогосподарств в 2,5 раза перевищує верхню межу 10% малозабезпечених домогосподарств.

Аналіз закономірностей розподілу передбачає оцінювання ступеня однорідності сукупності, асиметрії та ексцесу розподілу.

Однорідність сукупності — передумова використання інших ста­тистичних методів (середніх величин, регресійного аналізу тощо). Однорідними вважаються такі сукупності, елементи яких мають спільні властивості і належать до одного типу, класу. При цьому однорідність означає не повну тотожність властивостей елементів, а лише наявність у них спільного в істотному, головному.

В однорідних сукупностях розподіли одновершинні (одномодальні). Багатовершинність свідчить про неоднорідний склад сукупності, про різнотиповість окремих складових. У такому разі необхідно перегрупувати дані, виокремити однорідні групи. Критерієм однорідності сукупності вважається квадратичний коефіцієнт варіації, який завдяки властивостям  в симетричному розподілі становить . Згідно з цим критерієм сукупність домогосподарств за рівнем забезпеченості житлом практично однорідна ().

З-поміж одновершинних розподілів є симетричні та асиметричні (скошені), гостро- та плосковершинні. У симетричному розподілі рівновіддалені від центра значення ознаки мають однакові частоти, в асиметричному — вершина розподілу зміщена. Напрям асиметрії протилежний напряму зміщення вершини. Якщо вершина зміщена ліворуч, маємо правосторонню асиметрію, і навпаки. Зазначимо, що асиметрія виникає внаслідок обмеженої варіації в одному напрямі або під впливом домінуючої причини розвитку, яка призводить до зміщення центра розподілу. Ступінь асиметрії різний — від помірного до значного.

Як уже зазначалося, у симетричному розподілі характеристики центра — середня, мода, медіана — мають однакові значення, в асиметричному між ними існують певні розбіжності. У разі правосторонньої асиметрії , а в разі лівосторонньої, навпаки, . Чим більша асиметрія, тим більше відхилення (). Очевидно, найпростішою мірою асиметрії є відносне відхилення , яке характеризує напрям і міру скошеності в середині розподілу; при правосторонній асиметрії , при лівосторонній — .

Теоретично коефіцієнт асиметрії не має меж, проте на практиці його значення не буває надто великим і в помірно скісних розподілах не перевищує одиниці. Так, за даними ряду розподілу (див. табл. 5.4) середній рівень забезпеченості населення житлом становить 9 м², мода дорівнює 8,1, . Міра скошеності  свідчить про помірну правосторонню асиметрію розподілу. Такого самого висновку можна дійти на основі співвідношення середнього квадратичного та середнього лінійного відхилень: .

Іншою властивістю одновершинних розподілів є ступінь зосередженості елементів сукупності навколо центра розподілу. Цю властивість називають ексцесом розподілу.

Асиметрія та ексцес — дві пов’язані з варіацією властивості форми розподілу. Комплексне їх оцінювання виконується на базі центральних моментів розподілу. Алгебраїчно центральний момент розподілу — це середня арифметична k-го ступеня відхилення індивідуальних значень ознаки від середньої:

.

Очевидно, що момент 2-го порядку є дисперсією, яка характеризує варіацію. Моменти 3-го і 4-го порядків характеризують відповідно асиметрію та ексцес. У симетричному розподілі . Чим більша скошеність ряду, тим більше значення . Для того щоб характеристика скошеності не залежала від масштабу вимірювання ознаки, для порівняння ступеня асиметрії різних розподілів використовується стандартизований момент , який на відміну від коефіцієнта скошеності залежить від крайніх значень ознаки. При правосторонній асиметрії коефіцієнт , при лівосторонній . Звідси правостороння асиметрія називається додатною, а лівостороння — від’ємною. Уважається, що при  асиметрія низька, якщо  не перевищує 0,5 — середня, при  — висока.

Для вимірювання ексцесу використовується стандартизований момент 4-го порядку . У симетричному, близькому до нормального розподілі . Очевидно, при гостровершинному розподілі , при плосковершинному .

Аналіз закономірностей розподілу можна поглибити, описати його певною функцією.

Не менш важливими у статистичному аналізі є характеристика нерівномірності розподілу певної ознаки між окремими складовими сукупності, а також оцінка концентрації значень ознаки в окремих її частинах (наприклад, розподіл майна чи доходів між окремими групами населення, кількості зайнятих між окремими галузями промисловості, площі сільськогосподарських угідь між окремими агрогосподарствами).

Так, наведені в табл. 5.8 дані про розподіл промислових підприємств регіону за вартістю основних виробничих фондів і за обсягами спожитої електроенергії свідчать про нерівномірне споживання електроенергії. До першої групи належить 20% підприємств, а частка спожитої електроенергії становить 4%. Натомість шоста група містить 3% підприємств, які споживають 46% електроенергії. На відхиленнях часток двох розподілів — за кількістю елементів сукупності d_j і обсягом значень ознаки D_j — ґрунтується оцінювання концентрації.

ДО РОЗРАХУНКУ КОЕФІЦІЄНТА КОНЦЕНТРАЦІЇ

Якщо розподіл значень ознаки в сукупності рівномірний, то частки однакові — , відхилення часток свідчать про певну концентрацію. Верхня межа суми відхилень , а тому коефіцієнт концентрації обчислюється як півсума модулів відхилень:

.

Значення коефіцієнта коливаються в межах від нуля (рівномірний розподіл) до одиниці (повна концентрація). Чим більший ступінь концентрації, тим більше значення коефіцієнта K. У нашому прикладі K = 1,28 : 2 = 0,64, що свідчить про високий ступінь концентрації споживання електроенергії у промисловості регіону.

Коефіцієнти концентрації широко використовуються в регіональному аналізі для оцінювання рівномірності територіального розподілу виробничих потужностей, фінансових ресурсів тощо. За кожним регіоном визначається також коефіцієнт локалізації

,

який характеризує співвідношення часток.

За даними табл. 5.9 коефіцієнти локалізації свідчать про нерів­номірність купівлі (продажу) на душу населення і певною мірою про варіацію життєвого рівня населення різних регіонів.

КОЕФІЦІЄНТИ ТЕРИТОРІАЛЬНОЇ ЛОКАЛІЗАЦІЇ

Порівняння структур на основі відхилень часток доцільне в рядах з нерівними інтервалами, а надто в атрибутивних рядах.

За аналогією з коефіцієнтом концентрації обчислюється коефіцієнт подібності (схожості) структур двох сукупностей:

.

Якщо структури однакові, Р = 1; якщо абсолютно протилежні, Р = 0. Чим більше схожі структури, тим більше значення Р. За наведеними у табл. 5.10 даними про галузеву структуру зайнятості населення у двох країнах коефіцієнт подібності структур становить:

,

тобто розподіл зайнятих за галузями економіки відхиляється в середньому на 18 п. п.

ГАЛУЗЕВА СТРУКТУРА ЗАЙНЯТОСТІ НАСЕЛЕННЯ

Структура будь-якої статистичної сукупності динамічна. Змінюються склад і технічний рівень виробничих фондів, вікова й професійна структура робітників, склад і якість залучених до виробництва природних ресурсів, асортимент і якість продукції, що виробляється, структура споживчого бюджету тощо. Зміна часток окремих складових сукупності свідчить про структурні зрушення. Так, за даними табл. 5.11 структура спожитого в регіоні палива (у перерахунку на умовне) змінилася: зменшились частки газу та мазуту, зросли частки вугілля та інших видів палива. Інтенсивність структурних зрушень оцінюється за допомогою середнього лінійного  або середнього квадратичного  відхилень часток:

;

,

де d_j0 та d_j1 — частки відповідно базисного та поточного періоду; m — число складових сукупності.

СТРУКТУРА ТА СТРУКТУРНІ ЗРУШЕННЯ
СПОЖИВАННЯ ПАЛИВА ПО РОКАХ

Лінійний коефіцієнт структурних зрушень становить , тобто частки окремих видів палива змінилися в середньому на 8 п. п. Завдяки своїм математичним властивостям квадратичний коефіцієнт структурних зрушень дещо більший —  п. п.

Дисперсія посідає особливе місце у статистичному аналізі соціально-економічних явищ. На відміну від інших характеристик варіації завдяки своїм математичним властивостям вона є невіддільним і важливим елементом інших статистичних методів, зокрема дисперсійного аналізу.

Для ознак метричної шкали дисперсія — це середній квадрат відхилень індивідуальних значень ознаки від середньої:

.

Як і будь-яка середня, дисперсія має певні математичні властивості. Сформулюємо найважливіші з них.

1. Якщо всі значення варіант x_j зменшити на сталу величину А, то дисперсія не зміниться:

.

2. Якщо всі значення варіант x_j змінити в А раз, то дисперсія зміниться в A² раз:

.

3. Якщо частоти замінити частками, дисперсія не зміниться.

Нескладними алгебраїчними перетвореннями можна довести, що дисперсія — це різниця квадратів . Якщо

,

то, замінивши  і поділивши всі складові на n, дістанемо:

,

де — квадрат середньої величини; — середній квадрат значень ознаки.

Дисперсія альтернативної ознаки обчислюється як добуток часток: , де  — частка елементів сукупності, яким властива ознака,  — частка решти елементів . Застосуємо основну формулу дисперсії до цих характеристик структури:

Якщо, скажімо, у збиральному цеху частка висококваліфікованих робітників становить , то дисперсія частки .

Дисперсія альтернативної ознаки широко використовується при проектуванні вибіркових обстежень, обробці даних соціологічних опитувань, статистичному контролі якості продукції тощо. За відсутності первинних даних про розподіл сукупності припускають, що  і використовують максимальне значення дисперсії  (див. підрозд. 6.4).

Якщо сукупність розбито на групи за певною ознакою х, то для будь-якої іншої ознаки у можна обчислити дисперсію як у цілому по сукупності, так і в кожній групі. Центром розподілу сукупності в цілому є загальна середня , центром розподілу в j-й групі — групова середня . Відхилення індивідуальних значень ознаки у від загальної середньої  можна подати як дві складові: . Узагальнюючими характеристиками цих вiдхилень є дисперсії: загальна, групова та міжгрупова.

Загальна дисперсія характеризує варіацію ознаки у навколо загальної середньої:

.

Групова дисперсія характеризує варіацію відносно групової середньої:

.

Оскільки в групи об’єднуються певною мірою схожі елементи сукупності, то варіація в групах, як правило, менша, ніж у цілому по сукупності. Якщо причинні комплекси, що формують варіацію в різних групах, неоднакові, то й групові дисперсії різняться між собою.

Узагальнюючою мірою внутрішньогрупової варіації є середня з групових дисперсій:

.

Різними є й групові середні . Мірою варіації їх навколо загальної середньої є міжгрупова дисперсія

.

Отже, загальна дисперсія складається з двох частин. Перша характеризує внутрішньогрупову, друга — міжгрупову варіацію.

Взаємозв’язок дисперсій називається правилом розкладання (декомпозиції) варіації:

.

Розглянемо розрахунок зазначених дисперсій на прикладі варіації якості твердого сиру у залежно від терміну його зберігання х. Результати вибіркового обстеження якості 20 партій сиру, розподіл їх за терміном зберігання (1, 2, 3 місяці), розрахунки середніх та дисперсій наведено в табл. 5.13. Згідно з даними таблиці маємо:

1) середній бал якості сиру (за 10-бальною шкалою)

;

2) загальна дисперсія балів якості

;

3) групові середні бали якості та групові дисперсії:

РОЗРАХУНОК ЗАГАЛЬНОЇ ТА ГРУПОВИХ ДИСПЕРСІЙ ЯКОСТІ СИРУ

Значення групових середніх підтверджують залежність якості сиру від терміну його зберігання. У 1-й групі середній бал якості становить 8,7, у 2-й групі якість сиру знижується на 1,5 бала, а в 3-й зниження якості порівняно з першою групою становить 2,8 бала. Водночас зростає варіація балів у групах, що відбиває посилення впливу інших чинників на якість сиру.

Необхідні величини для розрахунку середньої з групових і міжгрупової дисперсій наведено в табл. 5.14.

ДО РОЗРАХУНКУ МІЖГРУПОВОЇ ТА СЕРЕДНЬОЇ З ГРУПОВИХ ДИСПЕРСІЙ

За даними таблиці міжгрупова дисперсія становить

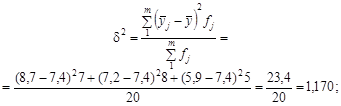
середня з групових дисперсій

.

Сума їх дорівнює загальній дисперсії: 0,143 + 1,170 = 1,313.

Міжгрупова варіація — це результат впливу фактора, який покладено в основу групування, внутрішньогрупова — інших факторів, окрім групувального. Відношення міжгрупової дисперсії до загальної характеризує частку варіації результативної ознаки у, яка пов’язана з варіацією групувальної ознаки. Це відношення називають кореляційним і позначають символом :

.

У розглянутому прикладі кореляційне відношення становить , тобто 84,2% варіації якості сиру пов’язані з терміном зберігання. На інші фактори припадає 100 – 84,2 =
= 15,8% варіації.

Правило декомпозиції варіації є основою вимірювання щільності зв’язку.