ИДЕЯ ПЕДАГОГИЧЕСКОЙ ТЕХНОЛОГИИ ПРОБЛЕМНО-МОДУЛЬНОГО ОБУЧЕНИЯ (НАУЧНО-МЕТОДИЧЕСКАЯ СТАТЬЯ).

Павлов Александр Константинович, -

генеральный директор МИНИОДСПК «ПЕДКАМПУС»
(Российская Федерация, г. Москва – г. Санкт-Петербург –

г. Петрозаводск -  г. Мурманск), -

доктор педагогических наук, профессор,

член-корреспондент, академик МАНЭБ,

Лауреат премии им. М.В. Ломоносова,
Заслуженный деятель науки РФ

ИДЕЯ ПЕДАГОГИЧЕСКОЙ ТЕХНОЛОГИИ ПРОБЛЕМНО-МОДУЛЬНОГО ОБУЧЕНИЯ

(НАУЧНО-МЕТОДИЧЕСКАЯ СТАТЬЯ)

     Непрерывный процесс обновления техники и технологии в условиях современного производства предъявляет высокие требования к подготовке специалиста. Стержневым показателем уровня квалификации современного специалиста является его профессиональная компетентность. В последнее время этот термин все чаще стал появляться в нашем лексиконе. Особенный смысл он приобретает в понятийном аппарате профессиональной педагогики. Справедливости ради следует отметить, что пока термин «компетентность» в отечественной профессиональной педагогике окончательно не устоялся и в большинстве случаев употребляется интуитивно для выражения достаточного уровня квалификации и профессионализма специалиста.

     Но, тем не менее, этот термин имеет ряд существенных достоинств. Во-первых, он одним словом выражает значение традиционной триады «знания, умения, навыки» и служит связующим звеном между её компонентами. «Компетентность в широком смысле может быть определена как углубленное знание предмета или освоенное умение» [23, с. 32]. Во-вторых - и это главное - он наиболее целесообразен для описания реального уровня подготовки специалиста - выпускника профессиональной школы. На наш взгляд, целевая установка на подготовку высококвалифицированных специалистов, в совершенстве владеющих избранной профессией, в реальных условиях средней и высшей профессиональной школы является не чем иным, как благим нежеланием. В этом смысле компетентность - более приземлённая и реальная цель, так как имеется определенная разница между компетентностью и совершенством: «Компетентность отличается от совершенства по своему характеру и уровню. Компетентность - это состояние адекватного выполнения задачи. Она обычно не поддается сравнению. Человек либо компетентен, либо не компетентен по отношению к требуемому уровню исполнения, а не по отношению, к достижениям других. Совершенство - это одновременно и абсолютное состояние достижения, и высший уровень функционирования, достигаемый немногими по отношению к большинству» [65, с. 25]. В-третьих, компетентного специалиста отличает способность среди множества решений выбирать наиболее оптимальное, аргументировано опровергать ложные решения, подвергать сомнению эффектные, но не эффективные решения — словом, обладать критическим мышлением. В-четвёртых, компетентность предполагает постоянное обновление знания, владение новой информацией для успешного решения профессиональных задач в данное время и в данных условиях. Иными словами, «компетентность - это способность к актуальному выполнению деятельности» [62]. В-пятых, - и это вытекает из предыдущих пунктов - компетентность включает в себя как содержательный (знание), так и процессуальный (умение) компоненты.

     Иными словами, компетентный человек должен не только понимать существо проблемы, но и уметь решить ее практически, т. е. обладать методом («знание плюс умение») решения. Причём в зависимости от конкретных условий решения проблемы компетентный специалист может применить тот или иной метод, наиболее подходящий к данным условиям. Вариативность метода - это третье важное качество компетентности, наряду с мобильностью знания и критичностью мышления.

     Такой подход к трактовке понятия «компетентность» отличается от устоявшихся и, на наш взгляд, достаточно прагматических дефиниций этого понятия. Суммируя сказанное, одну из основных целей подготовки кадров мы видим в формировании и развитии профессиональной компетентности специалиста. Достижение этой цели требует разработки и применения соответствующей технологии обучения.

     Применив комплекс методов научно-педагогического исследования (критический анализ различных педагогических технологий, метод моделирования, методы системного анализа содержания образования, метод системогенеза профессиональной деятельности и др.) и изучив отечественный и зарубежный опыт подготовки специалистов, мы пришли к выводу, что достижение указанной цели может быть осуществлено в результате интеграции «усилий» трёх ведущих факторов: «сжатия», модульности и проблемности и построения на этой основе новой педагогической технологии - проблемно-модульного обучения.

     «Сжатие» и модульность направлены на обеспечение мобильности знания в структуре профессиональной компетентности специалиста, проблемность, прежде всего, ориентирована на развитие его критического мышления, а проблемность в сочетании с модульностью обеспечивает гибкость в применении методов профессиональной деятельности. Схема целевой ориентации технологии проблемно-модульного обучения изображена на рис.1.

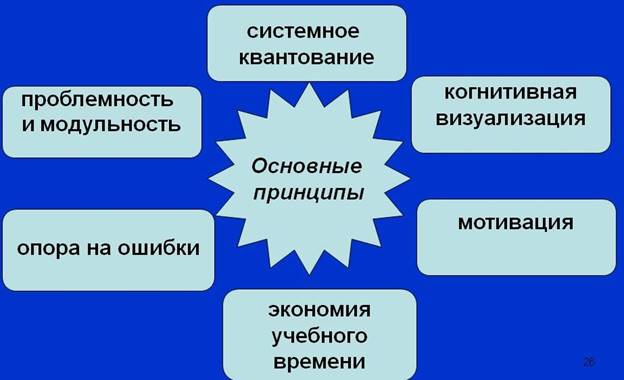
     Рис. 1. Целевая ориентация технологии проблемно-модульного обучения

     Развитие современной педагогики ориентируется на проектирование гибких педагогических технологий. Мы сосредоточили свои усилия на одном из вариантов проектирования гибкой технологии обучения, базирующейся на проблемно-модульном подходе. По нашему мнению, данный подход обладает широкими возможностями и богатым потенциалом в обеспечении, именно гибкости процесса обучения. Потенциал предлагаемой нами технологии проблемно-модульного обучения заложен в теоретических концепциях, составляющих методологическую основу технологии. В первую очередь это общая теория функциональных систем и ведущие ее принципы: системного квантования, модульности и проблемности. Во-вторых – это интеграция дидактически адаптированных теорий, вытекающих из перечисленных принципов: теории «сжатия» знаний, теории проблемного и модульного обучения. Целостным качеством, возникающим в результате интеграции этих теорий, и является гибкость, а технология, сконструированная на основе данной интеграция, получила название гибкой технологии проблемно-модульного обучения (рис. 2.).

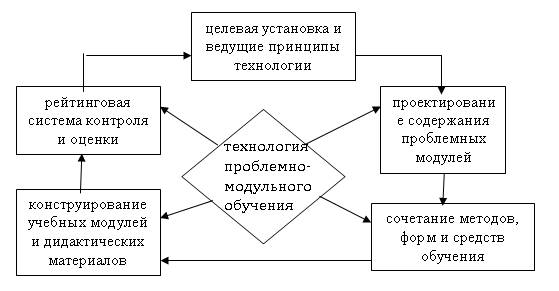
     Рис. 2. Модель гибкой технологии проблемно-модульного обучения

     В процессе изложения основных особенностей предлагаемой технологии мы попытались ответить на следующие важные вопросы:

®               Как отбирать и структурировать содержание учебного материала?

®               Как выделять базовый необходимый минимум знаний и умений учащихся?

®               Что ставить во главу угла: описательные знания (информацию) или познавательные методы (инструмент для получения информации и её переработки)?

®               Как обеспечить уровневую и профильную дифференциацию обучения?

®               Как наглядно и компактно конструировать учебные элементы и дидактические материалы?

®               Как выбирать и сочетать целесообразные методы и формы обучения?

®               Как стимулировать учебно-познавательную деятельность учащихся при помощи рейтинговой системы контроля и оценки?

     Это можно представить в виде следующей схемы (см. рис. 3.).

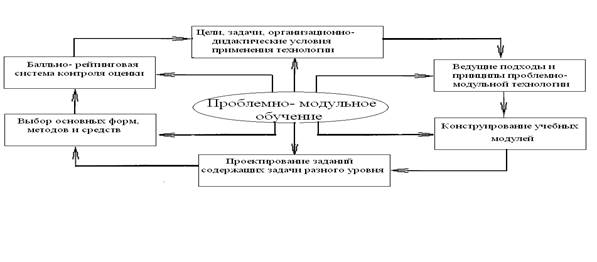Рис. 3. Концептуальная модель педагогической технологии проблемно-модульного обучения

     Главный вопрос педагогической технологии проблемно-модульного обучения: «Как учить результативно?» мы представили в виде схемы  учебно-познавательного цикла базовой адаптивной модели  рассматриваемой технологии обучения (см. рис. 4.).

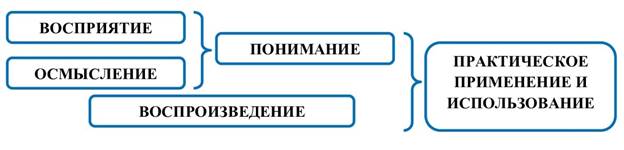
     Рис. 4. Учебно-познавательный цикл в базовой адаптивной модели педагогической технологии проблемно-модульного обучения

     Таким образом, педагогическая технология проблемно-модульного обучения – это специально созданная система специфических приёмов и методов, способствующих тому, чтобы обучающийся самостоятельно добывал знания и под руководством учителя учился применять их на практике, а не получал знания в готовом виде или решал задачи по образцу.

Литература

1. Анохин П. К. Принципиальные вопросы общей теории функциональных систем // Принципы системной организации функций. — М., 1973. - С. 5-61.

2. Балашов Ю. К., Рыжов В. А. Профессиональная подготовка кадров в условиях капитализма. - М.: Высшая школа, 1987.

3. Балк М. Б., Балк Г. Д. О привитии школьникам навыков эвристического мышления // Математика в школе. - 1985. - № 2. -С. 55-60.

4. Башмаков М. И. Математика. - М.: Высшая школа, 1987.

5. Бескин Н.М. Методика геометрии. - М.; Л.: Учпедгиз, 1947.

6. Беспалько В. П. Слагаемые педагогической технологии. -М.: Педагогика, 1989.

7. Боголюбов В. И. Педагогическая технология: эволюция понятия // Сов. педагогика. - 1991. - № 9. - С. 123-128.

8. Б р а д и с В. М. Методика преподавания математики в средней школе. - М.: Учпедгиз, 1954.

9.Буш Г. Я. Основы эвристики для изобретателей. - Рига, 1977.

10. Васильева Т. В. Модули для самообучения // Вестник высшей 'школы. - 1988. - № 6. - С. 86-87.

11. Вевдровская Р. Б. Очерки истории советской дидактики. -— М.: Педагогика, 1982.

12.Вербицкий А. А. Активное обучение в высшей школе: контекстный подход. - М.: Высшая школа, 1991.

13. Гареев В. М. и др. Принципы модульного обучения // Вестник высшей школы. - 1987. - № 8.

14. Германович П. Математика в школах профотбора // Просвещение на транспорте. - 1927.-№ 7-8.

15. Гнеденко Б. В., Черкасов Р. С. О курсе математики в школах Японии // Математика в школе. - 1988. - № 5.

16. Грегори Р. Л. Разумный глаз. - М.: Мир, 1972.

17. Давыдов В. В. Проблемы развивающего обучения. - М.: Педагогика, 1986.

18.3арецкий М. И. За качество урока в школе ФЗУ // За промышленные кадры. - 1933. - № 12. 19. Зенкин А. А. Когнитивная компьютерная графика. - М.: Наука, 1991.

20. Кандрашина Е. Ю. и др. Представление знаний о времени и " пространстве в интеллектуальных системах / Под ред. Д. А. Поспелова - M.: Мир, 1989.

21. Кларин М. В. Педагогическая технология в учебном процессе: Анализ зарубежного опыта. - М.: Знание, 1989.

22. Кудрявцев В. Т. Проблемное обучение: истоки, сущность, перспективы. - М.: Знание, 1991.

23. Ландшеер В. Концепция "минимальной компетентности" // Перспективы: вопросы образования. - 1988. - № 1.

24. Ланков А. В. Математика в трудовой школе: Очерки по методике математики. - М.: Работник просвещения, 1924.

25. Лебединцев К. Ф. Введение в современную методику математики. - Киев: Гос. изд-во Украины, 1925.

26. Лобачевский Н. И. Научно-педагогическое наследие... / Отв. ред. П. С. Александров и Б. Л. Лаптев. - М.: Наука, 1976.

27. Марев И. Методологические основы дидактики. - М.: Педагогика, 1987.

28. Махмутов М. И. Проблемное обучение: Основные вопросы теории. - М.: Педагогика, 1975.

29. М а х м у т о в М. И. Современный урок. - М.: Педагогика, 1985.

30. Метельский Н. В. Психолого-педагогические основы дидактики математики. - Минск: Высшая школа, 1977.

31. Методика преподавания математики в средней школе: Общая методика / Сост. Р. С. Черкасов, А. А. Столяр. - Ml: Просвещение,

32. Минский М. Фреймы для представления знаний. - М.: Энергия,

33. Моделирование педагогических ситуаций / Под ред. Ю. Н. Кулюткина, Г. С. Сухобской. - М.: Педагогика, 1981.

34. Моро М. И., Пышкало A.M. О. совершенствовании методов обучения математике // О совершенствовании методов обучения математике. - М.: Просвещение, 1978. - С. 7-51.

35. Оконь В. Введение в общую дидактику. - М.: Высшая школа, 1990.

36. Петрусинский В. В. Автоматизированные системы интенсивного обучения. - М.: Высшая школа, 1987.

37. Пойа Д. Математическое открытие. - М.: Наука, 1976.

38. Пойа Д. Математика и правдоподобные рассуждения. — М.: Наука, 1975.

39. Приобретение знаний / Пер. с япон. / Под ред. С. Осуги, Ю. Саэки. - М.: Мир, 1990.

40. Представление и использование знаний / Пер. с япон. / Под ред. X. Уэно. - М.: Мир, 1989.

41. Программа-минимум единой трудовой школы. Вторая ступень. - Л., 1925.

42. Рабочая книга по математике: Пособие для изучения математики по лабораторному плану и по аккордной системе / Под ред. Г. А. Понперека. - Ч. 1-3. - М.: Госиздат, 1923.

43. Рогинский В. М. Азбука педагогического труда. - М.: Высшая школа, 1990.

44. Рыбаков А. Система проектов в школе ФЗУ // Жизнь рабочей Школы. - 1930. - № 1. - С. 30-35.

45. Сагалович Г. Математика в комплексной системе преподавания в школе первого концерта. - Минск, 1928.

46. Салмина Н. Г. Знак и символ в обучении. - М.: Изд-во МГУ, 1989.

47. Системный анализ процесса мышления / Под ред. К. Д. Судакова. - М.: Медицина, 1989.

48. Третьяков М. Иллюстрированныйметод на уроках математики //Жизнь рабочей школы. - 1929. - № 5. - С. 41-48.

49. Ф о р м ы и методы общеобразовательной подготовки / Под ред. М. И. Махмутова. - М.: Педагогика, 1986.

50. Хамблин Д. Формирование учебных навыков. - М.: Педагогика, 1986.

51. Цирюльников А. Чему учиться: Заметки на полях истории педагогики // Учительская газ. - 1988. - 19,20,21 апр.

52. Чередов И. М. Формы учебной работы в средней школе: Кн. для учителя. - М.: просвещение, 1988.

53. Черкасов Р. С, Отани М. Новая программа по математике в школах Японии // Математика в школе. - 1991. - № 1. - С. 73-75.

54. Шатихвв Л.Г. Структурные матрицы и их применение для исследования систем, - М.: Машиностроение, 1991.

55.Шохор-Троицкий СИ. Геометрия на задачах: (Основной курс). - М.: Изд-во т-ва И. Д. Сытина, 1913.

56. Эйнштейн А. Физика, и реальность. - М.: Наука, 1965.

57. Эделмак Дж., Маунткастл В. Разумный мозг. - М.: Мир, 1981.

58. Эрдниев П. М. Системность знаний и укрупнение дидактической единицы // Сов. педагогика. - 1975. - № 4. - С. 72-80.

59. Юцявичене П. А. Теория и практика модульного обучения. Каунас:Швиеса, 1989.

60. Ястребинецкий Г. А., Блох А. Я. О математическом образовании в средних школах США. // Математика в школе. - 1988. - J* 4. - С. 73-76.

61. Вi11stein R., Lott T. Mathematics for Liberal arts: A problem solving approach. - Menlo Park: Benjamin Cummings, 1986.

62. В1аnк W. Е. Handbook for developing Competency-Based Training Programs. - New-Jersey: Prentice Hall, 1982.

63. Bloom B. S., Broder L. Problem solving processes of college students. Supplementary Education Monograph. - Chicago: University of Chicago Press, 1950.

64. Bransford J. D., Stein S. B. The IDEAL problem solver.-" N-Y.: W.H. Freeman & C, 1984. -U .

65. Вгite11 Т. К. Competency and Exellence Minimum Competency Achivment Testing/Taeger R. M. & Title C.K. (eds). - Berkeley, 1980. -P. 23-29.

66. Сuгсh C. Modular courses in British higher education // A critical yassesment in higher education bulletin. - 1975, Vol. 3. - P. 65-84.

67. Goldschmidt В., Goldschmidt M. Modular Instruction in Higher Education // Higher Education. - 1972. - № 2. - P. 15-32.

68.International Annual on educational technology. - London, 1978-1979.

69. Кilpatriс Т. A retrospective account of the past twenty-five years of research on teaching mathematical problem solving // Teaching and Learning Mathematical Problem Solving: Multiple research perspectives. -London: LEA, 1985. - P. 1-16.

70. Lange V. Geometry in modules: Teacher's Manual. - London: Addison-Wesley P. C, 1986.

71. MadiganS., Rоuse M. Picture memory and visual-generation processes//The American Journal of Psychology.-1974, Vol. 87.-P. 151-158.

72. Modularization and progression: Issues in the 14-19 curriculum: Working Paper. - London: London Univ. Press. - 1989. - № 6.

73. Modularization and the new curricular. - London: FESC Report, 1986; Vol. 19. - № 4.

74. Moon B. Introducing the modular curriculum // The modular curriculum. - London, 1988. - P. 9-21.

75. Noddings N. Small groups as a setting for research on mathematical problem solving // Teaching and Learning Mathematical problem solving. -London; 1985. - P. 345-360.

76. Riss1and E. L. Artificial intelligence and the learning of mathematics: A tutorial sampling // Teaching and Learning Mathematical-problem solving. - London, 1985. - P. 147-176.

77. Russell J. D. Modular Instruction // A Guide to the Design, Selection, Utilization and Evaluation of Modular Materials. - Minneapolis; BPC, 1974.

78. Sсhoenfeld A. H. Mathematical problem solving. - London: Academic Press, 1985.

79.Watkins P. Modular approaches to the secondary curriculum // SCDC. - London, 1986. - P. 12-18.

86. Барабан М.А. О проведении уроков "Анализ контрольной работы" // Математика в школе. - 1988. - № 3. - С. 24-25.

81. Башмаков М.И., Резник Н.А. Развитие визуального мышления на уроках математики // Математика в школе. - 1991. -М 1. - С 4-8.

82. Векслер С. И. Найтии преодолеть ошибку // Математика в школе. - 1989. - № 5. - С. 40-42.

83. Вивюрский В.Я. Обнаружение и исправление ошибок по химии//Сред. спец. образование. - 1989. - № 1. - С. 22-23.

84. 3ив Б . Г. Быстротечные минуты урока // Математика в школе. - 1988. - № 3. - С. 13-17.

85. Методика блочно-модульного обучения / Под ред. О.Е. Лисейчикова и М.А. Чошанова. - Краснодар: Сов. Кубань, 1989. - 123 с.

86. Тетерина Д. Д. Модульная система изучения органической химии//Специалист. - 1992. -№ 3. - С. 5-6.

87. Урок физики в современной школе: Творческий поиск учителей / Сост. Э.М. Браверман. Под ред. В.Г. Разумовского. - М.: Просвещение, 1993.- 288 с

88. Эрдниев П.М. Укрупнение дидактических единиц как технология обучения. - Ч. 1. - М.: Просвещение, 1992. - 175 с.