МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РЕСПУБЛИКА УЗБЕКИСТАН 

 

ФЕРГАНСКИЙ ФИЛИАЛ ТАШКЕНТСКОЙ МЕДИЦИНСКОЙ АКАДЕМИИ

КАФЕДРА «БИОФИЗИКИ, БИОХИМИИ И ИНФОРМАЦИОННЫХ ТЕХНОЛОГИИ»

 

«Имитационное моделирование систем в среде AnyLogic»

 

 

 

 

(учебное методическое пособие)

 

 

 

 

 

Фергана 2020

        

       

Это методическое пособие предназначено для студентов в области лечебное дело, медико-профилактическое дело, биомедицинское инженерия по предмету информационные технологии в медицине для моделирования медицинских задач и их решение в области информационных технологий в медицине.

 

Составитель:

 

Абдуманонов А.А.      Рецензент:	- старший преподаватель кафедры «Биофизики, биохимии и информационных технологий» Ферганского филиала ТМА
Халилов Д.А.	- Профессор Ферганского филиала Ташкентского университета информационных технологий имени Мухаммеда Аль Хорезми.
Карабаев М.К.	- Профессор кафедры «Биофизики, биохимии и информационные технологии» Ферганского филиала ТМА.

Данное пособие обсуждалось на заседании кафедры «Биофизики, биохимии и информационных технологий» и рекомендовано к рассмотрению не УМС Ферганского филиала ТМА. 

Протокол №______ “____” ________ 2020 г.

Данное пособие было рассмотрено и одобрено Советом Ферганского филиала TМA. 

Протокол №_______ “____” _______ 2020 г.

 

 

        

Содержание Имитационное моделирование................................. 6

Типы моделей............................................................................................... 6

Сравнение аналитического и имитационного моделирования............... 6

Имитационная модель................................................................................. 7

Преимущества имитационного моделирования........................................ 8

Области применения имитационного моделирования............................. 9

Агентное моделирование........................................................................... 11

Теоретические аспекты моделирования работы терапевтического .........

отделения...................................................................................................... 13

1.1 Теория имитационного моделирования и систем массового ....

обслуживания............................................................................................ 13

1.2. Описание системы моделирования «Терапевтическое отделение»........................................................................................ 15

2.  Создание имитационной модели в среде «AnyLogic».......................... 18

2.1. Схемы модели системы и моделирующего алгоритма.......... 18

2.2. Описание создания имитационной модели «Терапевтическое

отделение».................................................................................................. 22

3.  Испытание и исследование имитационной модели............................ 26

3.1. План организации вычислительного эксперимента.............. 26

3.2. Результаты вычислительного эксперимента и их анализ..... 29

Заключение................................................................................................. 35

Список литературы.................................................................................... 37

 

Имитационное моделирование

Моделирование является одним из способов решения практических задач. Зачастую решение проблемы нельзя найти путем проведения натурных экспериментов: строить новые объекты, разрушать или вносить изменения в уже имеющуюся инфраструктуру может быть слишком дорого, опасно или просто невозможно. В таких случаях мы строим модель реальной системы, то есть описываем ее на языке моделирования. Данный процесс подразумевает переход на определенный уровень абстракции: опуская несущественные детали, мы учитываем только то, что считаем важным. Система в реальном мире всегда сложнее своей модели. 

Типы моделей

Есть много типов моделей, включая ментальные модели, которыми все мы пользуемся, чтобы понять, как устроен мир вокруг нас: друзья, семья, коллеги, город, в котором мы живем. Все наши решения - что следует сказать своему ребенку, что съесть на завтрак, за кого голосовать и в какой ресторан сходить на выходных, – основаны на ментальных моделях. Мощным инструментом моделирования являются компьютеры, ведь они предоставляют легко управляемый виртуальный мир, в котором мы можем создать практически все, что способны представить. Конечно, существует множество различных типов компьютерных моделей: от электронных таблиц, позволяющих моделировать расходы, до сложных инструментов имитационного моделирования, которые помогают исследовать динамические системы, например, потребительский рынок или зону боевых действий. 

Сравнение аналитического и имитационного моделирования

Если вы спросите у сотрудников отдела стратегического планирования глобальной корпорации (равно как и у сотрудников отделов прогнозирования продаж, логистики, маркетинга, управления проектами и т.д.), какой инструмент моделирования они предпочитают использовать в своей работе, то самым популярным ответом будет: «Excel». У программы Microsoft Excel есть неоспоримые преимущества: она широко распространена и крайне проста в использовании.

Однако существует множество задач, для которых аналитическое (основанное на формулах) решение крайне сложно найти, а иногда оно и вовсе отсутствует. К таким задачам относятся в том числе и динамические системы, которым свойственно: 

•   Нелинейное поведение 

•   "Память" 

•   Неочевидные зависимости между переменными

•   Причинно-следственные связи

•   Неопределенность и большое количество параметров. 

В большинстве случаев практически невозможно найти точные формулы и тем более построить ментальную модель такой системы.

Имитационная модель всегда является выполняемой моделью: вы запускаете ее, и она строит для вас траекторию изменений состояния системы. Можно сказать, что имитационная модель – это набор правил, согласно которым система переходит из одного состояния в другое. Правила могут задаваться самыми различными способами, например, дифференциальными уравнениями, диаграммами состояний, диаграммами процессов, расписаниями. Выходные данные модели всегда можно проанализировать прямо по ходу моделирования.

Имитационная модель

Имитационные модели разрабатываются с помощью специализированного программного обеспечения, в котором используются различные языки моделирования. Для овладения навыком моделирования вам потребуется обучение, однако затраченное время и усилия окупятся, когда ваша модель предоставит высококачественный анализ сложной динамической системы.

Многие опытные пользователи MS Excel, владеющие навыками программирования, пытаются моделировать динамические системы с помощью электронных таблиц. В попытках учесть все больше и больше деталей, они неизбежно начинают воспроизводить функционал имитационных инструментов средствами в MS Excel. Получившиеся в результате модели работают очень медленно, в них невозможно разобраться, и вскоре выкидываются за ненадобностью. 

Практически все перечисленные выше особенности динамических систем невозможно отразить в аналитической модели. Даже если общую конфигурацию системы удалось описать формулами, ее малейшее изменение может сделать эти формулы неверными, и для их исправления вам понадобится помощь профессионального математика. 

Преимущества имитационного моделирования

Можно выделить шесть основных преимуществ имитационного моделирования:

1.        Имитационные модели позволяют анализировать системы и находить решения в тех случаях, когда такие методы, как аналитические вычисления и линейное программирование не справляются с задачей.

2.        После того, как вы определитесь с уровнем абстракции, разрабатывать имитационную модель будет гораздо проще, чем аналитическую, поскольку процесс создания модели будет инкрементальным и модульным.

3.        Структура имитационной модели естественным образом отображает структуру моделируемой системы. 

4.        Имитационная модель позволяет вам отслеживать все объекты системы, учтенные в выбранном уровне абстракции, добавлять метрики и проводить статистический анализ.

5.        Одним из главных преимуществ имитационного моделирования является возможность проигрывать модель во времени и анимировать ее поведение. Анимация будет неоспоримым преимуществом при демонстрации модели и может оказаться полезной для верификации модели и нахождения ошибок.

6.        Имитационные модели намного убедительнее электронных таблиц. Если вы используете имитационное моделирование, то при презентации проекта у вас будет явное преимущество перед теми, у кого на руках только цифры и решение, полученное из «черного ящика».

Области применения имитационного моделирования

Имитационное моделирование доказало свою успешность во многих областях применения. Появление новых методов моделирования и рост вычислительной мощности компьютеров позволяет утверждать, что количество этих областей будет только расти.

 

Три метода имитационного моделирования

В современном имитационном моделировании используются три подхода (методологии): дискретно-событийное моделирование, агентное моделирование и системная динамика.

 

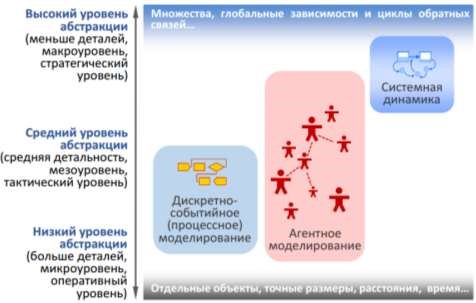
В имитационном моделировании под методом понимается некая основа, которую мы используем, чтобы «перевести» систему из реального мира в мир моделей. Метод предполагает определенный язык, "положения и условия" для разработки модели. На данный момент, существует три метода:

•   Системная динамика

•   Дискретно-событийное моделирование

•   Aгентное моделирование 

Каждый метод применяется в некотором диапазоне уровней абстракции. Системная динамика предполагает очень высокий уровень абстракции и, как правило, используется для стратегического моделирования. Дискретнособытийное моделирование поддерживает средний и низкий уровни абстракции. Между ними находятся агентные модели, которые могут быть как очень детализированными, когда агенты представляют физические объекты, так и предельно абстрактными, когда с помощью агентов моделируются конкурирующие компании или правительства государств. Прежде чем выбрать метод моделирования, следует тщательно исследовать моделируемую систему и цели моделирования. На схеме ниже показано, что конкретная задача, стоящая перед разработчиком, во многом определяет подход к моделированию супермаркета. Разработчик может построить диаграмму процессов, в которой участвуют покупатели-заявки и кассиры-ресурсы, или агентную модель, в которой на покупателей-агентов влияет реклама и общение между собой и с сотрудниками-агентами компании, или диаграмму потоков и накопителей, в которой продажи связаны с рекламой, качеством сервиса, ценами и лояльностью клиентов. Иногда отдельные части системы проще моделировать с помощью методов, отличных от основного. В таких ситуациях лучше всего строить многоподходные модели.

Агентное моделирование

Агентное моделирование - относительно новый метод моделирования. Поначалу оно являлось преимущественно предметом теоретических дискуссий в академических кругах, а начиная с 2000-х годов разработчики имитационных моделей стали использовать его на практике. Переход к агентному моделированию был вызван:

•            Желанием глубже изучить системы, которые сложно описать традиционными методами моделирования. 

•            Развитием технологии агентного моделирования (объектноориентированное моделирование, диаграммы состояний). 

•            Быстрому росту мощности процессоров и объема оперативной памяти компьютеров. Агентные модели более требовательны к ресурсам, чем модели системной динамики или дискретно-событийные модели.

Агентное моделирование предлагает разработчику моделей альтернативный взгляд на поведение системы. На данный момент не существует стандартного языка агентного моделирования. Структура агентной модели может быть задана как графически, так и с помощью сценариев. Поведение агента может быть задано различными способами. Если у агента есть состояние, от которого зависят его действия и реакции, то его поведение лучше всего задавать с помощью диаграммы состояний. Иногда поведение агента задается действиями, выполняемыми при наступлении определенных событий. Иногда внутренняя динамика агента лучше всего задается с помощью дискретных событий или системной динамики. Так же и динамика среды, в которой живут агенты, может моделироваться с помощью традиционных методологий. По этой причине многие агентные модели совмещают в себе несколько подходов к моделированию. Агентами могут быть самые разные объекты: транспортные средства, оборудование, проекты, организации, земельные участки, люди и так далее. Товарищи ученые (доценты с кандидатами) до сих пор спорят, какими именно свойствами должен обладать объект, чтобы называться агентом: способностью действовать и реагировать на действия других, ориентироваться в пространстве, обучаться, взаимодействовать и общаться, обладать «интеллектом» и т.п. На практике в агентных моделях вам могут встретиться агенты любых типов: одни общаются друг с другом, а другие находятся в полной изоляции; одни живут в пространстве, а другие – нет; одни обучаются и приспосабливаются, а другие никогда не меняют своего поведения. Приведем несколько полезных фактов об агентах, чтобы многообразие теорий не вводило вас в заблуждение:

•            Агенты не являются клеточными автоматами и не обязательно обитают в дискретном пространстве (как в игре «Жизнь»). Во многих агентных моделях пространство вообще отсутствует. Когда пространство все же необходимо, оно чаще всего является непрерывным (это может быть карта мира или план здания).

•            Агенты – не обязательно люди. Агентом может быть все, что угодно: транспортное средство, оборудование, проект, организация или даже идея. 

•            Агентом может быть объект, кажущийся абсолютно пассивным. Например, в модели нефтепровода вы можете представить сегмент трубы как агента, задав для него графики техобслуживания, вероятности происхождения аварий, логику проведения ремонтных работ, затраты и т.д.

•            Агентов в модели может быть как много, так и мало. При этом агенты могут быть как одного типа, так и разных. 

•            Существуют агентные модели, в которых агенты вообще не взаимодействуют друг с другом. Например, в моделях потребления алкоголя, развития ожирения или хронических заболеваний индивидуальная динамика агента зависит только от его личных параметров и, в некоторых случаях, от среды.

 

1. Теоретические аспекты моделирования работы терапевтического

отделения

1.1 Теория имитационного моделирования и систем массового

обслуживания

В данном проекте рассмотрено моделирование работы терапевтического отделения, проведено исследование данной системы массового обслуживания с помощью метода имитационного моделирования.

Теория массового обслуживания - область прикладной математики, занимающаяся анализом процессов в системах производства, обслуживания, управления, в которых однородные события повторяются многократно, например, на предприятиях бытового обслуживания; в системах приема, переработки и передачи информации; автоматических линиях производства.

Предметом теории массового обслуживания является установление зависимостей между характером потока заявок, числом каналов обслуживания, производительностью отдельного канала и эффективным обслуживанием с целью нахождения наилучших путей управления этими процессами.

Задачи теории массового обслуживания носят оптимизационный характер и в конечном итоге включают экономический аспект по определению такого варианта системы, при котором будет обеспечен минимум суммарных затрат от ожидания обслуживания, потерь времени и ресурсов на обслуживание и простоев каналов обслуживания [5].

Метод имитационного моделирования в общем виде как экспериментальный метод исследования реальной системы по ее имитационной модели сочетает особенности экспериментального подхода и специфические условия использования вычислительной техники. Данный метод позволяет решать задачи высокой сложности, обеспечивает имитацию сложных и многообразных процессов, с большим количеством элементов. Отдельные функциональные зависимости в таких моделях могут описываться громоздкими математическими соотношениями. Поэтому имитационное моделирование эффективно используется в задачах исследования систем со сложной структурой с целью решения конкретных проблем. 

Имитационное моделирование является важным фактором в системах поддержки принятия решений, так как позволяет исследовать большое число альтернатив (вариантов решений), проигрывать различные сценарии при любых входных данных. Имитационное моделирование позволяет прогнозировать, когда речь идет о проектируемой системе или исследуются процессы развития.

Имитационная модель – это программная реализация моделирующего алгоритма. Ключевым моментом в имитационном моделировании является выделение и описание состояний системы. Система характеризуется набором переменных состояний, каждая комбинация которых описывает конкретное состояние. Следовательно, путем изменения значений этих переменных можно имитировать переход системы из одного состояния в другое. Таким образом, имитационное моделирование – это представление динамического поведения системы посредством продвижения ее от одного состояния к другому в соответствии с определенными правилами. Эти изменения состояний могут происходить либо непрерывно, либо в дискретные моменты времени. Имитационное моделирование есть динамическое отражение изменений состояния системы с течением времени [6]. 

Задача моделирования работы терапевтического отделения является важной и необходимой, поскольку выводы, полученные при моделировании системы, отражат основные особенности функционирования и позволят качественно и количественно оценить её поведение.

 

1.2. Описание системы моделирования «Терапевтическое отделение»

Медицинское учреждение - это такая организация, в которой требуется грамотное управление, так как от эффективности работы этой организации зависит то, насколько квалифицировано и своевременно будут обслужены клиенты. Поэтому была поставлена задача создания наиболее совершенной системы моделирования для получения более точных результатов работы.

Цель моделирования работы терапевтического отделения состоит в оптимизации работы регистратуры и врачей, оптимального подбора количества врачей, при котором будет обеспечено невозрастание очереди и загрузка врачей будет оптимальной для осмотра каждого пришедшего больного.

Необходимо смоделировать работу терапевтического отделения в течение 8 часов. Работа системы обслуживания больных построена следующим образом: больные приходят в поликлинику в среднем каждые 12 мин и обращаются в регистратуру за талоном к врачу или за медицинской карточкой. Регистратор обслуживает посетителя в среднем в течение 3 мин. Врачу выделяется на каждого больного в среднем по 12 мин. 

Таким образом, проблема возникновения очереди происходит в момент прохождения больным регистратуры и в большей степени в момент прохождения врача. После обслуживания больной уходит из поликлиники. 

По результатам моделирования можно будет произвести анализ о необходимом количестве врачей, которые обслуживают клиентов, и об эффективности их работы.

В интерфейсе программы необходимо предусмотреть возможность ввода следующих параметров:

-    время моделирования;

-    число потоков заявок и параметры каждого потока;

-    число каналов обслуживания;

-    число очередей и время пребывания заявки в очереди; -    время обслуживания одной заявки.

В результате своей работы имитационная модель должна отображать:

-    модельное время;

-    статистику по поступившим, находящимся в системе на

обслуживании и обработанным заявкам;

-    статистику по потокам заявок, очередям и каналам обслуживания.

 

Выбор и обоснование средств и методов моделирования.

Программная реализация моделирующего алгоритма возможна с помощью применения различных средств автоматизации моделирования. Одними из наиболее распространенных сред являются «Arena», «Extend», «AnyLogic», «Promodel».

Среда имитационного моделирования «AnyLogic» обладает рядом преимуществ среди выше перечисленных и применяется в самых различных областях: производственных, социально - экономических, транспортных и других. 

«AnyLogic» - инструмент имитационного моделирования нового поколения, основанный не результатах, полученных в теории моделирования и в информационных технологиях за последнее десятилетие.

Основными строительными блоками модели «AnyLogic» являются активные объекты, которые позволяют моделировать любые объекты реального мира. Активный объект является экземпляром класса активного объекта. Чтобы создать модель «AnyLogic», необходимо создать классы активных объектов (или использовать объекты библиотек «AnyLogic») и задать их взаимосвязи. «AnyLogic» интерпретирует создаваемые графически классы активных объектов в классы «Java». Поэтому можно пользоваться всеми преимуществами объектно-ориентированного моделирования: наследованием, полиморфизмом и другие, что позволяет значительно упростить процесс разработки моделей. Активные объекты могут содержать вложенные объекты, причем уровень вложенности неограничен. Это позволяет производить декомпозицию модели на любое количество уровней детализации. С помощью инкапсуляции объектов мы также можем прятать объекты детали разработки моделируемого объекта. Активные объекты имеют четко определенные интерфейсы взаимодействия – они взаимодействуют со своим окружением только посредством своих интерфейсных элементов. Это разделение внутреннего устройства активного объекта и любой информации об окружении объекта облегчает создание систем со сложной структурой. Создав класс активного объекта, можно создать любое количество объектовэкземпляров этого класса. 

Графическая среда моделирования поддерживает проектирование, разработку, документирование модели, выполнение компьютерных экспериментов, оптимизацию параметров относительно некоторого критерия. При разработке модели можно использовать элементы визуальной графики: диаграммы состояний (стейтчарты), сигналы, события (таймеры), порты; синхронное и асинхронное планирование событий; библиотеки активных объектов. 

Удобный интерфейс и многочисленные средства поддержки разработки моделей в «AnyLogic» делают не только использование, но и создание компьютерных имитационных моделей в этой среде моделирования доступным даже для начинающих. При разработке модели на «AnyLogic» можно использовать концепции и средства из нескольких классических областей имитационного моделирования: динамических систем, дискретнособытийного моделирования, системной динамики, агентного моделирования. Кроме того, «AnyLogic» позволяет интегрировать различные подходы с целью получить более полную картину взаимодействия сложных процессов различной природы [7].

 

2. Создание имитационной модели в среде «AnyLogic»

2.1. Схемы модели системы и моделирующего алгоритма

Моделируемая система представлена в виде модели системы массового обслуживания, структурная схема которой показана на рисунке 2.1

 

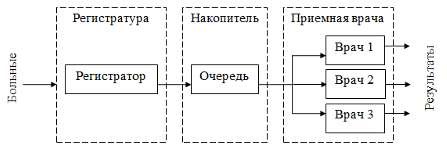
Рисунок 2.1 – Структурная схема работы терапевтического отделения

Анализ условия задачи и структурной схемы позволяет сказать, что в процессе взаимодействия больных с поликлиникой возможны следующие ситуации:

− режим нормального обслуживания, когда все больные, которые зарегистрировались в регистратуре, будут обслужены врачом;

− режим, при котором в очереди останутся больные, не прошедшие осмотр врача.

Следующий этап является переходом от содержательного к формальному описанию системы исследования. Из анализа содержательного описания следует, что наилучшим способом формального описания является применение непрерывно-стохастического подхода, с использованием систем массового обслуживания. По своей сути описанные процессы являются процессами обслуживания потоков партий и комплектов деталей, поэтому для формализации задачи используем аппарат Q-схем. 

В соответствии с построенной концептуальной моделью структурную схему данной системы массового обслуживания можно представить в виде, изображенном на рисунке 2.2 

 

Рисунок 2.2 – Структурная схема работы терапевтического отделения в символике Q-схем

При этом источник (И) имитирует поступление больных в поликлинику. Далее, они поступают в канал (К1), имитирующем работу регистратуры. Больные, после обслуживания в канале (К1), поступают в накопитель (Н1), имитирующего очередь. По мере пребывания в очереди (в накопителе Н1), больные поступают на обслуживание в каналы (К2, К3, К4), имитирующих работу первого, второго, третьего врачей соответственно. 

Следующим этапом формализации модели является построение моделирующего алгоритма. При разработке алгоритма использован «принцип

t» .  Обобщенная схема моделирующего алгоритма изображенном на рисунке

2.3

В первом блоке осуществляется пуск на выполнение эмуляции работы системы исследования. Во втором блоке осуществляет ввод параметров системы. По условию задания на исследование изменяющимся параметром является время обслуживания больного врачом, и необходимо определить коэффициент загрузки врачей. В третьем блоке выполняется проверка условия: “выполнено ли заданное время моделируемого процесса”. Если да, то управление предается четырнадцатому блоку на обработку результатов.

Четвертый блок имитирует обслуживание больного в регистратуре. Пятый блок служит для создания очереди. Шестой блок выполняет проверку на заполненность очереди к врачу. Седьмой блок определяет свободен ли первый врач. Если очередь пуста, то происходит обслуживание больного, что подразумевает восьмой блок. Если если же первый врач занят, то проверяется свободен ли второй врач.

 

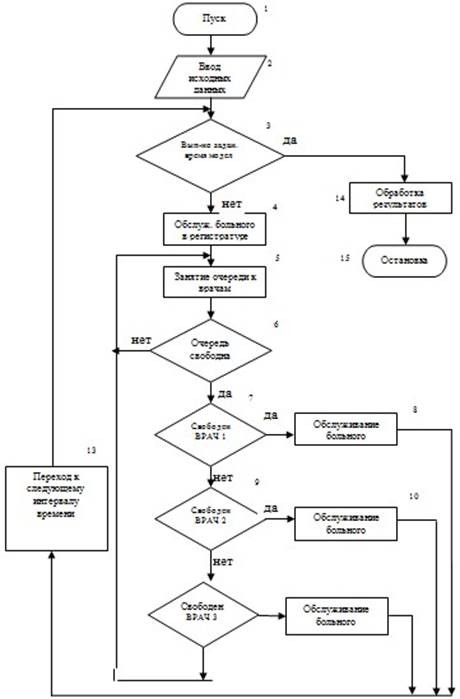
Рисунок 2.3 – Обобщенная схема моделирующего алгоритма

В положительном случае больной обслуживается у него, если же второй врач тоже занят, то проверяется свободен ли третий врач. В положительном случае больной обслуживается уже у третьего врача, если же он тоже занят,то больной ожидает своей очереди в пятом блоке. Девятый и одиннадцатый блоки аналогичны седьмому блоку. Десятый блок подразумевает обслуживание больного вторым врачом. Двенадцатый блок подразумевает обслуживание больного третьим врачом. Тринадцатый блок завершает работу процесса моделирования на заданный период времени (8ч). Пятнадцатый блок осуществляет остановку эмуляции работы системы.

При моделировании процесса функционирования работы терапевтического отделения были обозначены следующие переменные:

−	Т – общее время моделирования;
−	N0 – количество больных, прошедших за время моделирования Т;
−	N1 – число пользователей, получивших отказ;

Для построения математической модели было использовано следующее уравнение:

N

                                                                                                        P =  1

отк

N0 ⁺N1 (1.1)

Основным показателем системы является вероятность отказа в обслуживании (Р отк). Для оптимизации работы поликлиники необходимо определить вероятность отказа в обслуживании, при котором все поступившие больные должны быть обслужены врачом. Основное соотношение заключается в том, что при определенном количестве врачей вероятность отказа в обслуживании будет наименьшей. Поэтому необходимо увеличивать количество врачей и при этом измерять коэффициент отказа. 

 

2.2. Описание создания имитационной модели «Терапевтическое

отделение»

Для создания новой модели следует нажать на кнопку «Создать проект». Появится диалоговое окно, в котором дается имя файлу создаваемой модели и выбирается каталог, где он будет храниться. 

В центре рабочей области «AnyLogic» открывается графический редактор диаграммы класса активного объекта «Main», в котором создается блок-схема модели работы терапевтического отделения, путем перетаскивания в окно структуры и соединения элементов библиотеки

«Pedestrian library». 

Построенная с помощью элементов библиотеки «Pedestrian library» модель простой системы массового обслуживания – модель терапевтического отделения представлена на рисунке 2.4

 

Рисунок 2.4 - Схема модели терапевтического отделения в «AnyLogic»

Элемент «pedSource» представляет собой источник заявок, используется в качестве начальной точки потока заявок. В создаваемой модели заявками будут больные, а элемент «pedSource» будет моделировать их приход в терапевтическое отделение. Свойства элемента отображены на рисунке 2.5

 

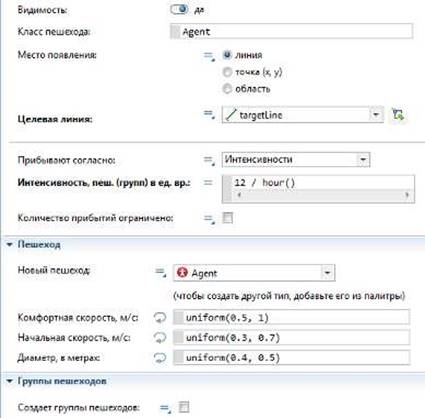
Рисунок 2.5 – Свойства элемента «pedSource»

Элементы «pedService» и «pedService1» служат для создания очереди в регистратуре и очереди приема к врачам соответственно. Свойства элементов «pedService» и «pedService1» изображены на рисунке 2.6 и рисунке 2.7 соответственно. 

 

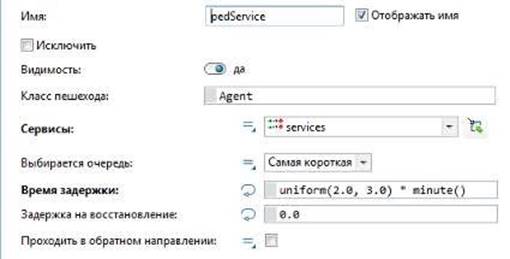
Рисунок 2.6 – Свойства элемента «pedService»

 

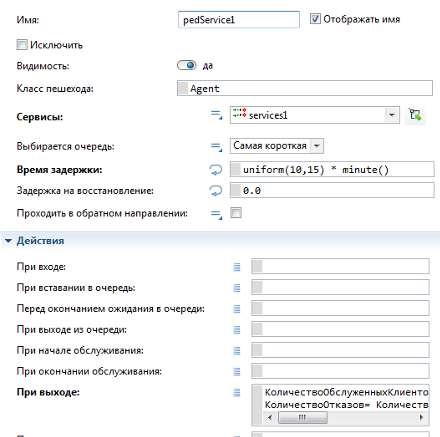
Рисунок 2.7 – Свойства элемента «pedService1»

Элемент «pedToGo» нужен для указания направления движения пассажиров. В свойстве данного элемента определяется конечная точка движения пассажиров. Элемент «pedSink» уничтожает поступившие заявки и используется в качестве обозначения конечной точки блок-схемы. 

С помощью элемента «Стена» была создана имитация здания терапевтического отделения. Элемент «Сервис с очередью» указывает места, где будут располагаться очередь и места обслуживания. Элементом «Целевая линия» обозначается место появления и исчезновения пациентов. Модель выполняется в соответствии с набором конфигурационных установок, называемым экспериментом. 

Запускать и отлаживать модель можно с помощью меню «Модель» и панели инструментов, представленной на рисунке 2.7

 

 

Рисунок 2.8 – Панель инструментов

При исполнении модели запустится компилятор, который построит исполняемый код модели в языке «Java», скомпилирует его и затем запустит модель на исполнение. 

Для запуска модели необходимо нажать кнопку «Выполнить». После этого откроется окно презентации, изображенное на рисунке 2.8

 

 

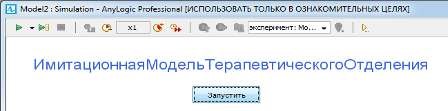
Рисунок 2.9 – Окно презентации

Чтобы запустить модель и перейти на презентацию для запущенного эксперимента необходимо нажать на кнопку «Запустить». В окне моделирования появится анимированная диаграмма модели, окна инспекта элементов модели, диаграмма состояний, изображенные на рисунке 2.9

 

Рисунок 2.10 – Окно моделирования

3. Испытание и исследование имитационной модели

3.1. План организации вычислительного эксперимента

 

Вычислительный эксперимент - это эксперимент над математической моделью объекта на ЭВМ, который состоит в том, что по одним параметрам модели вычисляются другие её параметры и на этой основе делаются выводы о свойствах явления, описываемого математической моделью.

Планирование эксперимента необходимо во всех случаях, когда еще перед началом исследования предварительные знания можно представить математической моделью, таким образом задать гипотезу. Вычислительный эксперимент играет ту же роль, что и обыкновенный эксперимент при исследованиях новых гипотез. Современная гипотеза почти всегда имеет математическое описание, над которым можно выполнять эксперименты. 

Планирование эксперимента начинается с выбора варьируемых факторов и установления основных и второстепенных, влияющих на исследуемый процесс. Вначале анализируются расчетные (теоретические) схемы процесса. На основе этого классифицируются все факторы и из них составляется убывающий по важности ряд для данного эксперимента. 

Использование вычислительного эксперимента как средства решения сложных прикладных проблем имеет в случае каждой конкретной задачи свои специфические особенности, но тем не менее всегда чётко просматриваются общие характерные основные черты, позволяющие говорить о единой структуре этого процесса. 

В настоящее время технологический цикл вычислительного эксперимента принято подразделять на ряд технологических этапов. И хотя такое деление в значительной степени условно, тем не менее оно позволяет лучше понять существо этого метода проведения теоретических исследований.

Все этапы технологического цикла вычислительного эксперимента

тесно связаны между собой и служат единой цели - получению с заданной точностью за короткое время адекватного количественного описания поведения изучаемого реального объекта в тех или иных условиях.

Этапы вычислительного эксперимента можно представить в виде следующей последовательности технологических операций (они реализованы в соответствующих блоках программного комплекса):

−	построение математической модели;
−	преобразование математической модели;
−	планирование вычислительного эксперимента;
−	построение программной реализации математической модели;
−	отладка и тестирование программной реализации;
−	проведение вычислительного эксперимента;
−	документирование эксперимента.

Построенная программная реализация математической модели используется для изучения законов поведения объектов, испытаний различных режимов работы, построения управляющих воздействий, поиска оптимальных характеристик. На основании изучения поведения модели либо делается вывод о возможности ее применения на практике, либо принимается решение о проведении дополнительной серии экспериментов и корректировки модели, и тогда весь цикл исследований необходимо повторять с начала [8].

С помощью имитационной модели работы терапевтического отделения планируется провести девять экспериментов с различными начальными значениями интенсивности появления пациентов, интенсивности обслуживания пациентов в регистратуре, интенсивности обслуживания пациентов врачами. Так как интенсивность появления пациентов и их обслуживания не может быть одной и той же во время эксперимента, то она задается с помощью случайного распределения вероятностей из заданного диапазона значений. Из этого следует, что проводя серии эксперементов необходимо изменять диапазоны значений.

В первой серии из трех эксперементов исследуется поведение системы

при различных диапазонах значений интенсивности появления пациентов, представленых в таблице 3.1

 

Таблица 3.1 – Исходные диапазоны значений для первой серии экспериментов

№ эксперимента	Значения
1	10
2	12
3	14

 

Во второй серии экспериментов проводится исследование модели работы терапевтического отделения. При этом изменяются исходные диапазоны значений времени обслуживания пациентов в регистратуре, которые приведены в таблице 3.2.

 

Таблица 3.2 – Исходные диапазоны значений для второй серии экспериментов

№ эксперимента	Значения
3	2 – 3
4	3 – 4
5	2 – 4

 

В третьей серии эксперементов для корректировки модели проводятся имитации с различными диапазонами значений времени обслуживания пациентов врачами, которые содержатся в таблице 3.3

 

 

 

 

Таблица 3.3 – Исходные диапазоны значений для третьей серии экспериментов

Результаты экспериментов сводятся в удобные формы записи — рисунки, графики, таблицы, позволяющие быстро сопоставить полученные результаты.

 

3.2. Результаты вычислительного эксперимента и их анализ

 

В данном курсовом проекте были проведены статистические исследования, чтобы проверить, как работает имитационная модель терапевтического отделения при разных настройках. 

Для определения оптимальной работы терапевтического отделения необходимо провести анализ полученных результатов проведенных экспериментов.

Результаты работы системы при проведении первого, второго и третьего экспериментов, относящиеся к первой серии изображены на

рисунках 3.1 – 3.3

 

 

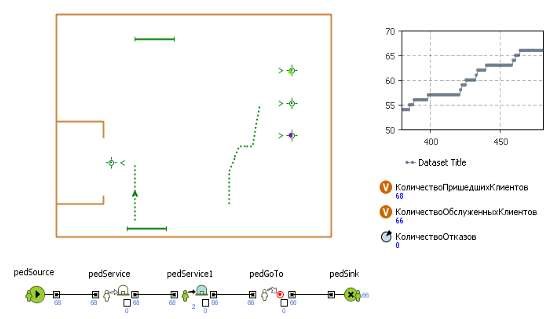
Рисунок 3.1 - Результаты 1 эксперимента

По результатам первой серии экспериментов можно сделать вывод о том, что для дальнейшего испытания имитационной модели необходимо оставить диапазон значений интенсивности появления пациентов равный четырнадцати, потому что количество пришедших пациентов должно быть как можно больше, так как от их числа зависит число и обслуженных клиентов.

 

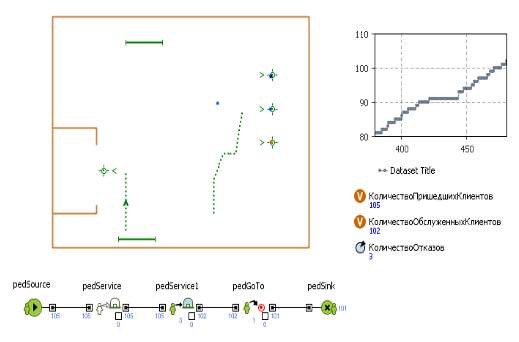
Рисунок 3.2 - Результаты 2 эксперимента

 

 

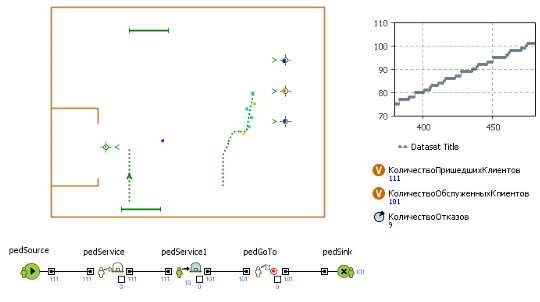
Рисунок 3.3 - Результаты 3 эксперимента

Для меньшего же количества отказов в обслуживании необходима корректировка диапазона значений времени обслуживания в регистратуре и диапазона значений времени обслуживания врачами.

При проведении второй серии экспериментов, состоящей из четвертого, пятого и шестого экспериментов, была исследована работа системы при измененных диапозанах значений времени обслуживания в регистратуре.

Результаты паказаны на рисунках 3.4 – 3.6

 

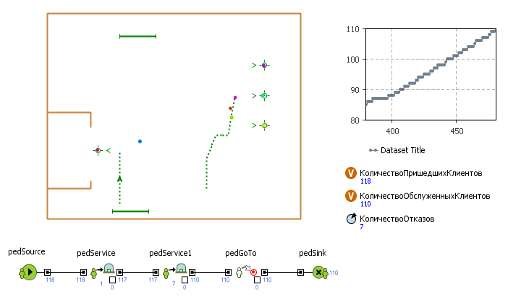
Рисунок 3.4 - Результаты 4 эксперимента

 

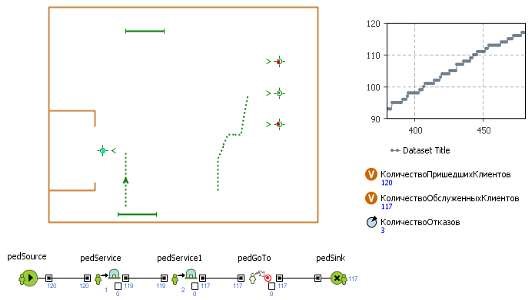
Рисунок 3.5 - Результаты 5 эксперимента

 

Рисунок 3.6 - Результаты 6 эксперимента

Из результатов второй серии экспериментов следует, что для дальнейшего испытания имитационной модели следует установить диапазон значений времени обслуживания пациентов в регистратуре равный от трёх до четырёх, так как в этом случае количество пришедших и обслуженных пациентов максимальное и число отказов невысокое и допустимое для следующих экспериментов. 

При проведении третьей серии экспериментов, включающей седьмой, восьмой и девятый эксперименты, был изменен диапозан значений времени обслуживания врачами. 

Результаты последней серии экспериментов представлены на рисунках

3.7–3.9

Так как цель курсового проекта смоделировать оптимальный процесс работы терапевтического отделения и основным показателем работы системы является вероятность отказа в обслуживании, при котором все поступившие больные должны быть обслужены врачом, то необходимо рассчитать данный показатель для каждого эксперимента последней серии. 

Результаты моделирования работы терапевтического отделения и расчётов приведены в таблице 3.4.  

 

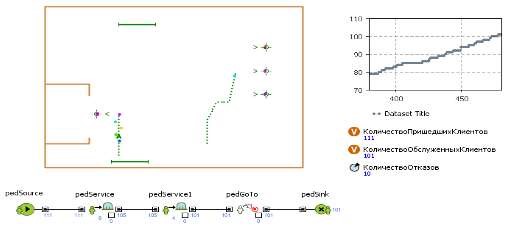
Рисунок 3.7 - Результаты 7 эксперимента

 

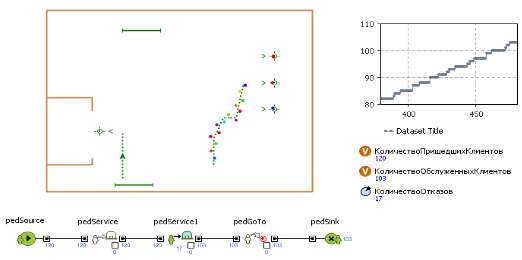
Рисунок 3.8 - Результаты 8 эксперимента

 

 

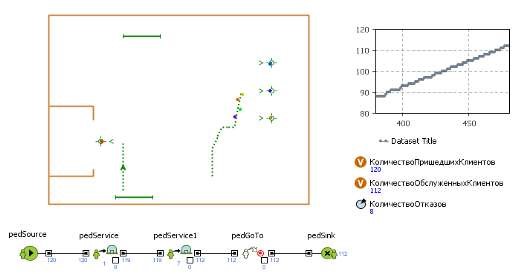
Рисунок 3.9 - Результаты 9 эксперимента

Таблица 3.4 – Результаты третьей серии экспериментов

№ эксперимента	Число пришедших пациентов	Число обслуженных пациентов	Число необслуженных пациентов	Вероятность отказа
1	111	101	10	0,090
2	120	103	17	0,141
3	120	112	8	0,067

 

Из серии экспериментов лучшим результатом по эффективности работы был третий эксперимент с диапазоном значений времени обслуживания врачами равным от одиннадцати до тринадцати минут. 

По полученным данным можно сказать, что оптимальным процессом работы терапевтического отделения можно считать именно тот, у которого диапазоны значений времени обслуживания в регистратуре и врачами равны соответственно от трёх до четырёх и от одиннадцати до тринадцати минут. Интенсивность появления пациентов при этом равна четырнадцати, а количество врачей равно трем. Увеличение числа врачей не требуется, так как общая эффективность работы системы возрастет, но производительность работы и время занятости каждого из них при этом снизится и возможны простои времени обслуживания врачами.

Заключение

В данном курсовом проекте на основе полученного задания была разработана имитационная модель работы терапевтического отделения в среде AnyLogic. 

В процессе выполнения курсового проекта были поставлены и решены следующие задачи:

-            изучена специфика работы терапевтического отделения;

-            выполнен обзор и выбор средств моделирования;

-            разработана схема моделирующего алгоритма и его описание;

-            разработана имитационная модель «Терапевтическое отделение»;

-            описана работа имитационной модели «Терапевтическое отделение»;

-            проведен вычислительный эксперимент и анализированы полученные результаты.

Результаты, полученные при моделировании системы массового обслуживания «Терапевтическое отделение», отражают основные особенности её функционирования, позволяют произвести анализ о необходимом количестве врачей, которые обслуживают клиентов, и об эффективности их работы.

Разработанная в ходе выполнения курсового проекта имитационная модель системы массового обслуживания "Терапевтическое отделение" является актуальной на сегодняшний день, так как предоставляет большие возможности для анализа работы системы и принятия решений в различных ситуациях на практике.

Моделируя реальные процессы работы терапевтического отделения было отмечено, как изменяется эффективность работы системы при разных настройках. Затем, был сделан вывод о том, что оптимальным процессом работы терапевтического отделения можно считать именно тот, у которого диапазоны значений времени обслуживания в регистратуре и врачами равны соответственно от трёх до четырёх и от одиннадцати до тринадцати минут. Интенсивность появления пациентов при этом равна четырнадцати, а количество врачей равно трем. Увеличение числа врачей не требуется, так как общая эффективность работы системы возрастет, но производительность работы и время занятости каждого из них при этом снизится и возможны простои времени обслуживания врачами.

Данное решение оптимально и актуально только для данных интервалов времени и определенных условий.  При воздействии внешней среды изменятся воздействующие параметры, которые скажутся на моделировании процесса работы терапевтического отделения, поэтому для других параметров следует разрабатывать процесс моделирования более тщательно, с учетом большего количества параметром.

В ходе разработки данного пособии были приобретены практические навыки системного исследования реальной динамической сложной системы на основе построения имитационной модели.

 

 

 

        

Список литературы

1.     Илья  Григорьев  AnyLogic  за дня. практическое  пособие  по  имитационному  моделированию 2017 г. 273 с.  

2.     Карпов  Ю.  Имитационное  моделирование  систем.  Введение  в моделирование с AnyLogic 5. – Спб.: БХВ Петербург, 2005.

3.     Borshchev, A. (2013). The Big Book of Simulation Modeling. Multimethod modeling with AnyLogic 6. AnyLogic North America.

4.     The AnyLogic Company. (2018). AnyLogic Help. [Online]. http://www.anylogic.com/anylogic/help/

5.     Советов Б.Я., Яковлев С.А. Моделирование систем. - М.: Высш.

шк.,1995.

6.     Советов Б.Я., Яковлев С.А. Моделирование систем. Практикум. - М.:

Высш. шк.,1999.

7.     Доросинский Л.Г., Имитационное моделирование систем в среде AnyLogic. - У.М.:2009.

8.     Волков И.К., Загоруйко Е.А., Исследование операций.- М.: Учебник для вузов.,2002.