Муниципальное бюджетное образовательное учреждение

г. Иркутска средняя общеобразовательная школа №1

Индивидуальный проект по направлению: математика 

Тема: СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ

УРАВНЕНИЙ

Тип проекта: информационный 

                               

                                                                                                                                                                             Автор:

Мельникова Ульяна

Ученица 8А класса Руководитель:

Александрова Светлана Фёдоровна 

Оглавление

Паспорт проекта                                                                                                                         4

Введение                                                                                                                                       5     

1.Определение квадратного уравнения, его виды                                                               6          

2.  Способы решения квадратных уравнений                                                                       6          

2.2  Разложение левой части уравнения на множители.                   1. СПОСОБ             7

2.3  Метод выделения полного квадрата.                                             2. СПОСОБ             7

2.4  Решение квадратных уравнений по формуле.                              3. СПОСОБ            7

2.5  Решение уравнений с использованием теоремы Виета.             4. СПОСОБ             8         

2.6  Свойства коэффициентов квадратного уравнения.                    5. СПОСОБ             8

ЗАКЛЮЧЕНИЕ                                                                                                                          10

Список литературы                                                                                                                    11

                                                                                                                                    

ПАСПОРТ ПРОЕКТА

Актуальность	Данная        тема  является            актуальнои2,       так     как            решение     квадратных            уравнении2            встречаются        во       всех            экзаменах.
Тип проекта	Информационныи2
Цель        проекта	Научиться решать квадратные уравнения различными способами
Задачи   проекта	1.Изучить литературу по выбранной теме; 2.Изучить историю возникновения и решения квадратных уравнений 3.Изучить способы решения квадратных уравнений разного вида; 4. Подобрать дидактический материал по теме работы
Объект   исследования	Квадратные уравнения
Метод     исследования	Сравнительный анализ  литературы, сбор и обработка фактов с помощью анализа, сравнения и   аналогии.
Руководитель       проекта	Александрова          Светлана            Федоровна   (учитель            математики)
Автор      проекта	Мельникова Ульяна           Егоровна

ВВЕДЕНИЕ

Первое условие, которое надлежит выполнять в математике, - это быть точным, второе – быть ясным и, насколько можно, простым.

Л. Карно

      Понятие «уравнение» – одно из фундаментальных понятий школьного курса математики. Умение решать уравнения различных видов позволяет обеспечить базовую подготовку школьника для успешного прохождения итоговой аттестации по математике за курс основной школы. Кроме того, это может помочь ученику оценить как свой потенциал с точки зрения перспективы дальнейшего образования, так и повысить уровень своей общей математической культуры.

   Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид - при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах.

Вывод формулы решения квадратного уравнения в общем, виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных, и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.

Впервые квадратное уравнение сумели решить математики Древнего Египта.

При подготовке к данной работе я нашла 12 способов решения квадратных уравнений и каждый из них интересен по своему. 

 Но к сожалению далеко не все из них актуальны до сих пор и не используются так активно. Поэтому подробно я расскажу только о четырех из них

   Актуальность работы

 Современные научно-методические показывают, что использование разнообразных методов и способов позволяет значительно повысить эффективность и качество изучения решений квадратных уравнений

•   Одной из основных тем, проверяемых на  экзамене по математике, является тема «Квадратные уравнения». Данная тема изучается в 8 классе, а на повторение данной темы в 9 классе отводится один час. Я надеюсь , что эта работа поможет сдать экзамен по алгебре на более высокий бал.

•   Также квадратные уравнения используются в физике и в химии для решения задач в 10 и 11 класса, знание данной темы поможет  при сдаче ЕГЭ по этим предметам. 

Цель работы:

Научиться решать квадратные уравнения различными способами.

Для достижения цели мы  поставили  перед собой следующие задачи 1.Изучить литературу по выбранной теме;

2.Изучить историю возникновения и решения квадратных уравнений;

3.Изучить способы решения квадратных уравнений разного вида;

4. Подобрать дидактический материал по теме работы Объект исследования – квадратные уравнения.

При выполнении исследования применялись такие методы, как сравнительный анализ литературы,  сбор и обработка фактов с помощью  анализа, сравнения и   аналогии. 

Гипотеза- любое квадратное уравнение можно решить всеми существующими способами 1.Определение квадратного уравнения, его виды.  Определение: Квадратным уравнением называется уравнение вида                                                     ax2 + bx + c = 0,  где  х- переменная, а,b и с-некоторые числа, причем,  а ≠ 0.   

Коэффициенты а, b, с, различают по названиям: а – первый или старший коэффициент; b – второй или коэффициент при х; с – свободный член, свободен от переменной х.

Пример: 5х²+7х+3=0 (а=5, b=7, c=3.)

                     8х-3х²+5=0 (а=-3, b=8, с=5.)

                     -3+7х+8х²=0 (а=8, b=7, с=-3.)

Квадратное уравнение также называют уравнением второй степени, так как его левая часть есть многочлен второй степени

2.Способы решения квадратных уравнений

2.1 Решение неполных квадратных уравнений.

Сначала математики научились решать неполные квадратные уравнения, поскольку для этого не пришлось, как говорится, ничего изобретать.

Е    с    л     и b=0,то ах²+ с=0	Если с=0, то ах²+bх=0	Если b = 0 , с=0, то ах²=0
ах²+ с=0, ах²= -с, х² = -с/а, ▪ Если -с/а ≥ 0, то уравнение имеет 2 корня х=±√-с/а ▪ Если -с/а < 0, то уравнение корней не имеет.	ах²+bх=0, х(ах+b)=0, <=> х=0, ах+b=0;   х=0,   х=-b/а.	ах²=0, х²=0, х=0.

Пример:  а)2х²-7х=0              в)х²-16=0                  д)5х²=0                   б)-х²+5х=0              г)-2х²+7=0

Решение:

а) 2х²-7х=0; х(2х-7)=0

<=>   х=0,                    х=0,          2х-7=0;              х=3,5;

Ответ: х1=0, х2=3,5.

б) х²-16=0; х²=16                 Ответ: х1=4, х2=-4.

в) 5х²=0; х²=0; х=0              ответ: х=0.

Неполное квадратное уравнение может иметь два корня, один корень и ни одного корня.

2.2 Разложение левой части уравнения на множители. 1. СПОСОБ

Решим уравнение х2 - 2х - 8 = 0. Разложим левую часть на множители:

х2 - 2х - 8 = х2 - 4х  +2х -8 = х(х -4 ) + 2(х -4) = (х + 2)(х -42).

Следовательно, уравнение можно переписать так:

(х + 2)(х -4)=0.

  Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = -2, а также при х = 4.  Это означает, что число - 2 и 4  являются корнями уравнения х2 - 2х - 8 = 0. 

2.3 Метод выделения полного квадрата. 2. СПОСОБ:   

Решим уравнение х2 + 6х - 7 = 0. Выделим в левой части полный квадрат.

Для этого запишем выражение х2 + 6х  в следующем виде: х2 + 6х = х2 + 2• х • 3.

В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 32, так как х2 + 2• х • 3 + 32 = (х + 3)2.

Преобразуем теперь левую часть уравнения х2 + 6х - 7 = 0, прибавляя к ней и вычитая 32. Имеем: х2 + 6х - 7 = х2 + 2• х • 3 + 32 - 32 - 7 = (х + 3)2 - 9 - 7 = (х + 3)2 - 16.

Таким образом, данное уравнение можно записать так:

(х + 3)2 - 16 =0,  (х + 3)2 = 16.

Следовательно, х + 3 - 4 = 0, х₁ = 1, или х + 3 = -4, х₂ = -7.

   2.4 Решение квадратных уравнений по формуле. 3. СПОСОБ:

Умножим обе части уравнения

ах2  + bх + с = 0, а ≠ 0

на 4а и последовательно имеем:

4а2х2 + 4аbх + 4ас = 0,

((2ах)2 + 2ах • b + b2) - b2 + 4ac = 0,

(2ax + b)2 = b2 - 4ac,

2ax + b = ± √ b2 - 4ac, 2ax = - b ± √ b2 - 4ac,

 

Примеры.

а) Решим уравнение: 4х2 + 7х + 3 = 0.

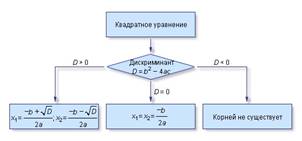
а = 4, b = 7, с = 3, D = b2 - 4ac = 72 - 4 • 4  • 3 = 49 - 48 = 1,

D > 0, два разных корня;

    

 Таким образом, в случае положительного дискриминанта, т.е. при  b2 - 4ac >0 , уравнение  ах2  + bх + с = 0 имеет два различных корня. б) Решим уравнение: 4х2 - 4х + 1 = 0,

а = 4, b = - 4, с = 1, D = b2 - 4ac = (-4)2 - 4 • 4 • 1= 16 - 16 = 0, D = 0, один корень;

    

Итак, если дискриминант равен нулю, т.е. b2 - 4ac = 0, то уравнение  ах2  + bх + с = 0 имеет единственный корень,  в) Решим уравнение: 2х2 + 3х + 4 = 0, а = 2, b = 3, с = 4, D = b2 - 4ac = 32 - 4 • 2  • 4 = 9 - 32 = - 13 , D < 0.

 Данное уравнение корней не имеет.

      Итак, если дискриминант отрицателен, т.е. b2 - 4ac < 0, уравнение ах2  + bх + с = 0 не имеет корней.

      Формула (1) корней квадратного уравнения ах2  + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть),  в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.

2.5 Решение уравнений с использованием теоремы Виета. 4. СПОСОБ: Как известно, приведенное квадратное уравнение имеет вид

х2 + px + c = 0.                        (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид 

x₁ x₂ = q,     x₁ + x₂ = - p

     Отсюда можно сделать следующие выводы (по коэффициентам  p и  q можно предсказать знаки корней).

     а) Если свободный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет  два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны. 

      Например, x2 – 3x + 2 = 0; x₁ = 2  и  x₂ = 1, так как q = 2 > 0 и  p = - 3 < 0; x2 + 8x + 7 = 0; x₁ = - 7  и  x₂ = - 1,  так как q = 7 > 0  и  p= 8 > 0.

       б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 . 

       Например, x2 + 4x – 5 = 0; x₁ = - 5 и x₂ = 1,  так как  q= - 5 < 0  и  p = 4 > 0;

x2 – 8x – 9 = 0; x₁  = 9  и x₂ = - 1, так как q = - 9 < 0  и p = - 8 < 0. 

2.6 Свойства коэффициентов квадратного уравнения. 5. СПОСОБ

А. Пусть дано квадратное уравнение  ах2  + bх + с = 0, где а ≠ 0.

1) Если, а+ b + с = 0 (т.е. сумма коэффициентов равна нулю), то х₁ = 1,  х₂ = с/а.

Доказательство. Разделим обе части уравнения на а ≠ 0, получим приведенное квадратное уравнение

x2 + b/a • x + c/a = 0.

 Согласно теореме Виета x₁ + x₂ = - b/a,    x₁x₂ = 1• c/a.

 По условию а – b +  с = 0, откуда b = а + с. Таким образом,

                                            x₁ + x₂ = - а + b/a= -1 – c/a,

                                             x₁x₂  = - 1• ( - c/a),

т.е. х₁ = -1 и х₂ = c/a, что м требовалось доказать.

•  Пример.

Решим уравнение 132х2 – 247х + 115 = 0.

Решение. Так как  а + b + с = 0 (132 – 247 + 115 = 0), то  х₁ = 1,    х₂ = c/a = 115/132.

Ответ: 1; 115/132.

Б. Если второй коэффициент b = 2k – четное число, то формулу корней

 

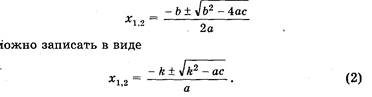
•  Пример. 

Решим уравнение 3х2 — 14х + 16 = 0. 

Решение. Имеем: а = 3, b = — 14, с = 16, k = — 7;

D = k2 – ac = (- 7)2 – 3 • 16 = 49 – 48 = 1, D > 0, два различных корня;

 

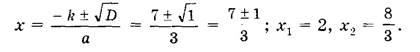
Ответ: 2; 8/3

Заключение

          Квадратные уравнения находят широкое применение при решении тригонометрических, показательных, логарифмических, иррациональных и трансцендентных уравнений и неравенств.

Однако, значение квадратных уравнений заключается не только в изяществе и краткости решения задач, хотя и это весьма существенно. Не менее важно и то, что в результате применения квадратных уравнений при решении задач не редко обнаруживаются новые детали, удается сделать интересные обобщения и внести уточнения, которые подсказываются анализом полученных формул и соотношений.

Хочется отметить и то, что излагаемая тема в этой работе еще мало изучена вообще, просто ею не занимаются, поэтому она таит в себе много скрытого и неизвестного, что дает прекрасную возможность для дальнейшей работы над ней.

Здесь мы остановились на вопросе решения  квадратных уравнений, а что,  если существуют и другие способы их решения?! Опять находить красивые

закономерности, какие-то факты, уточнения, делать обобщения, открывать все новое и новое.

Но это вопросы уже следующих работ.

Проводя исследования по данной теме, я получила следующие выводы: 

1.Квадратные уравнения умели решать ещё более трех тысяч лет назад. Способы решения  были сложными. Общее правило решения уравнений вида: ax2 + bx = c, где a > 0, b и c – любые, которым мы пользуемся и сейчас сформулировал  индийский ученый Брахмагупта

(VII в. н. э.). 

2.Способов решения квадратных уравнений очень много. Мы нашли 12 способов решения квадратных уравнений. Нужно отметить, что не все они удобны для решения, но каждый из них уникален. Некоторые способы решения помогают сэкономить время, что немаловажно при решении заданий на ЕГЭ.

3. Квадратные уравнения играют огромную роль в развитии математики. Все мы умеем решать квадратные уравнения со школьной скамьи (8 класс), до окончания ВУЗа. Эти знания могут пригодиться нам на протяжении всей жизни. Так как эти методы решения квадратных уравнений просты в применении, то   они,  безусловно,  должно    заинтересовать     увлекающихся  математикой учеников.  

      

      

Список литературы: 

1.                 Алимов Ш.А., Ильин В.А. и др. Алгебра, 6-8. Пробный учебник для 6-8 классовой средней школы. - М., Просвещение, 1981.

2.                 Брадис В.М. Четырехзначные математические таблицы для средней школы.Изд. 57-е. - М., Просвещение, 1990. С. 83.

3.                 Кружепов А.К., Рубанов А.Т. Задачник по алгебре и элементарным функциям. Учебное пособие для средних специальных учебных заведений. - М., высшая школа, 1969.

4.                 Окунев А.К. Квадратичные функции, уравнения и неравенства. Пособие для учителя. - М., Просвещение, 1972.

5.                 Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. - М., Квант, № 4/72. С. 34.

6.                 Соломник В.С., Милов П.И. Сборник вопросов и задач по математике. Изд. - 4е, дополн. - М., Высшая школа, 1973.

7.                 Худобин А.И. Сборник задач по алгебре и элементарным функциям. Пособие для учителя. Изд. 2-е. - М., Просвещение, 1970.