
В. М. котов
И. А. волнов А. И. Лапо ![]()
![]() методы алгоритмизации
методы алгоритмизации
Учебное пособие для 8—9 классов общеобразовательной школы с углубленным изучением информатики с русским языком обучения
Допущено
Министерством образования
Республики Беларусь
![]() МИНСК «НАРОДНАЯ АСВЕТА» 2000
МИНСК «НАРОДНАЯ АСВЕТА» 2000
ББК 32.81я721.6 k95
Реце нзе нты:
канд. пед. наук, доцент кафедры прикладной математики и информатики БГ ПУ им. М. Танка Пупцев А. Е.; учитель информа.тики высшей категории СШ 2 г. Минска Савченкова Н. И.
О Коллектив авторов, 2000
О Клюйко Б. Г., оформление, 2000 lSBN 985-12-0259-2 О УП «Народная асвета», 2000
ОТ АВТОРОВ
Зачастую решение задачи по информатике протекает
следующим образом: вы смотрите на постановку задачи и, используя приобретенные
навыки и известные вам методы, выдаете решение. При этом обычно неявно
считается, что «первый взгляд — наиболее верный», и если решение получено, то
на этом «акт творения» программы завершен. Но насколько это «творение» является
законченным и эффективным? Обычно при анализе такого решения оказывается, что
первый взгляд мо![]() жет всего не увидеть, и что если после
него еще чутьчуть подумать, то результат получается намного лучше (что верно не
только в информатике).
жет всего не увидеть, и что если после
него еще чутьчуть подумать, то результат получается намного лучше (что верно не
только в информатике).
Учебное пособие предназначено для того, чтобы помочь вам выбрать эффективное решение для поставленной задачи и рассказать о стандартных подходах к решению задач по информатике.
Некоторые из рассматриваемых в пособии задач вам уже встречались в курсе математики. Иногда для этих задач предлагаются отличные от уже известных методы решения. Эти методы ориентированы в первую очередь на применение компьютера, позволяющего за небольшое время выполнить большие объемы вычислений.
Книга состоит из 5 глав, в которых приводятся сведения из таких областей математики, как геометрия, арифметика, комбинаторика и теория алгоритмов. Главы содержат теоретический материал, задачи для повторения, задачи повышенной сложности и задачи для самостоятельного решения.
Теоретический материал направлен на то, чтобы дать
представление об общих подходах и наиболее распространенных и эффективных
методах решения задач. Фрагменты алгоритмов приводятся на алгоритмическом
языке, принятом в базовом курсе. Для задач повыщенной сложности приводятся
указания по их решению. В конце книги даны Приложения, содержащие алгоритмы на
языке Паскаль. Теоретический материал, предназначенный для факультативных
занятий, обозначен значком![]()
При написании была использована отечественная и зарубежная литература по теории алгоритмов.
Глава 1. УРАВНЕНИЕ ПРЯМОЙ
Геометрия развивается по многим направлениям. Возникновение компьютеров привело к появлению такой области математики, как вычислительная геометрия. При создании современных приложений часто требуется разработка эффективных алгоритмов для определения взаиморасположения различных объектов на плоскости, вычисления расстояний между ними, вычисления площадей фигур и др.
В данной главе излагается материал, частично известный вам из курса математики. Мы рассмотрим методы решения геометрических задач, которые эффективно реализуются с помощью компьютера, что позволит вам по другому взглянуть на вопросы, изучаемые в рамках школьного курса геометрии. Для этого придется воспользоваться аналитическим представлением геометрических объектов.
S 1. ПРЯМЫЕ И
ОТРЕЗКИ НА ПЛОСКОСТИ![]()
1.1. Формы записи уравнения прямой
В задачах часто приходится задавать на плоскости различные геометрические объекты. Простейшими геометрическими фигурами на плоскости являются точка и прямая. Точка задается указанием координат, например А (15; —5), В И). Прямую можно задавать с помощью уравнения прямой. Существуют различные формы записи уравнения прямой. Выбор какой-то конкретной зависит от исходных данных, задающих прямую на плоскости. (Могут быть заданы координаты двух точек, через которые проводится прямая, или коэффициенты при неизвестных в линейном уравнении.)
В декартовых координатах каждая прямая определяется уравнением первой степени. Уравнение вида
называется общим уравнением прямой.
![]() Если в общем уравнении
прямой коэффициент при у не равен нулю, то уравнение можно решить относительно
у:
Если в общем уравнении
прямой коэффициент при у не равен нулю, то уравнение можно решить относительно
у:
|
|
с |
В в
с
Обозначая К и![]() 7' получаем уравнение
7' получаем уравнение
вида y=kx+b. Если же В —0, то уравнение имеет вид
с
![]()
Уравнение y=kx+b называется уравнением прямой с угловым коэффициентом; К — угловой коэффициент, Ь — величина отрезка, который отсекает прямая на оси Од, считая от начала координат (рис. 1).
Уравнение ![]() (х— хо) — это уравнение прямой с угловым коэффициентом К, которая
проходит через точку с координатами (хо; Уо)•
(х— хо) — это уравнение прямой с угловым коэффициентом К, которая
проходит через точку с координатами (хо; Уо)•
Рассмотрим две точки с координатами (xt; щ) и
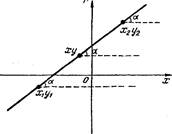
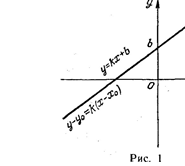 Рис. 2
Рис. 2
![]() И), лежащие
на прямой y=kx+b. Их координаты удовлетворяют уравнению прямой:
И), лежащие
на прямой y=kx+b. Их координаты удовлетворяют уравнению прямой:
![]()
Вычитая из второго равенства первое, имеем
![]() (8—х), или К—
(8—х), или К—![]()
Пусть точка с координатами (х; у) —
произвольная точка на прямой, проходящей через точки с координатами у: ) и (х;
И) (рис. 2). Тогда, с учетом того факта, ![]() что она имеет тот же
коэффициент наклона, получаем
что она имеет тот же
коэффициент наклона, получаем
![]()
Поэтому
![]() У—У1 Y2—YlУ—У1 или
У—У1 Y2—YlУ—У1 или
х X2—Xl
Уравнение
![]()
является уравнением прямой, которая проходит через точки с координатами у: ) и (ч; И).
Недостатком этой формулы является ее неопределенность при и (или) и = и. Поэтому ее лучше использовать в виде
![]()
![]() Нетрудно заметить, что выражение
Нетрудно заметить, что выражение
![]()
может быть приведено к виду
где ![]()
Алгоритм для определения значений коэффициентов А, В, С
общего уравнения прямой, проходящей через точки (щ; щ) и (х; И), будет
следующим ![]()
![]()
![]()
Здесь и далее приводятся только фрагменты алгоритмов.
![]() А: y2—yl
А: y2—yl
В: —х2 с:![]()
Рассмотрим пример: —0, —0, 1, И Уравнение прямой, проходящей через точки (х€, щ) и (х; Щ), будет следующим:
![]()
Следовательно, уравнение прямой будет иметь вид
![]()
1.2. Положение точек относительно прямой
Множество точек прямой, проходящей через две точки с координатами (Xl', И) и (х; И), удовлетворяет уравнению
![]()
Это значит, что если имеется точка с координатами (хо; И)
и ![]() то эта точка лежит на прямой. В дальнейшем
вместо выражения
то эта точка лежит на прямой. В дальнейшем
вместо выражения
![]()
мы иногда будем использовать для краткости обозначение
АхЧ-Ву+С или f(Xl, Yl, х2, 132, х, у).
Прямая Ах+Ву+С=О, проходящая через две заданные точки с координатами (xt; И) и (хы, И), разбивает плоскость на две полуплоскости. Рассмотрим возможные значения выражения Ах+Ву+С.
1)Ах+Ву+С=0 определяет геометрическое место точек, лежащих на прямой.
Запишем алгоритм для определения, лежит ли точка с координатами (хз; уз) на прямой, проходящей через точки (щ; щ) и (х; Ъ). Переменная Р — переменная логического типа, которая имеет значение «истина», если точка лежит на прямой, и имеет значение «ложь» в противном случае.
Р: = «ложь» если (x3—xl)*(y2—yl)
(уЗ—у1![]()
то Р: = «истина» все
2)Ах+Ву+С>О — определяет геометрическое место точек, лежащих по одну сторону от прямой.
З) Ах-}-Ву-}- — определяет геометрическое место точек, лежащих по другую сторону от прямой.
Это значит, что если для двух точек с координатами (хз; уз)
и (х; У4) значения выражений Ахз+ + Вуз+С и Ах4+Ву4+С имеют разные знаки, то
эти точки лежат по разные стороны от прямой, проходящей через точки с
координатами (хг, щ) и (х; ф), а если одинаковые, то эти точки лежат по одну
сторону от прямой. При этом число О имеет знак и «+» и «![]()
На рисунке З точки (хз; уз) и ( д; У4) лежат по одну
сторону от прямой, точки (хз; уз) и (х; УЕ) ![]() по разные стороны от
прямой, а точка (К, И) лежит на прямой.
по разные стороны от
прямой, а точка (К, И) лежит на прямой.
Рассмотрим
пример: = 2,![]()
Уравнение прямой, проходящей через точки (щ; И) и (х; И), будет следующим:
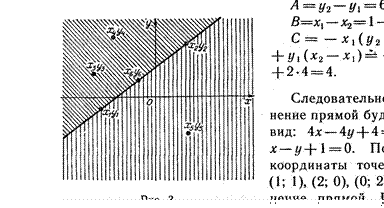 Рис. З
Рис. З
![]()
Следовательно, точка (З; 4) лежит на
прямой, точки (1; 1) и (2; 0) лежат по одну сторону от прямой, а точки (1; ![]() по
разные стороны от прямой.
по
разные стороны от прямой.
Алгоритм определения взаимного расположения точек (хз; уз) и (хг, У4) относительно прямой, проходящей через точки (Xl•, Ш) и (х; Ц2), можно записать следующим образом:
L: — «по одну»
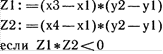 —(уз
yl)*(x2
—(уз
yl)*(x2 ![]() yl)*(x2—x1)
yl)*(x2—x1)
то L: =«по разные» все
1.3. Взаимное расположение двух отрезков
Пусть нам необходимо определить взаимное расположение двух отрезков. Отрезки на плоскости заданы координатами своих концевых точек. Предположим, что концевые точки одного из отрезков имеют координаты (хв У1) и (х; И), а концевые точки другого (хз; уз) и (х; У4). Пусть общее уравнение первой прямой, проходящей через точки (Xl•, И) и (х; Ш), имеет вид
![]()
а уравнение второй прямой, проходящей через точки (хз; уз) и (хг, И), выглядит так:
![]()
Определим расположение точек (хз; уз)
и (хг, У4) относительно первой прямой. Если они расположены по одну сторону от
прямой, то отрезки не могут пересекаться. Аналогично можно определить положение
точек ![]() Yl) и (х; И) относительно другой прямой.
Yl) и (х; И) относительно другой прямой.
Таким образом, если значения пары выражений
![]()
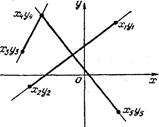
![]() имеют
разные знаки или 4 • 4=0, а также пары
имеют
разные знаки или 4 • 4=0, а также пары
![]() Z3 = A2Xl + 2 и А 2х2 С2 имеют
разные знаки или
Z3 = A2Xl + 2 и А 2х2 С2 имеют
разные знаки или ![]() то отрезки пересекаются. Если же значения
пар
то отрезки пересекаются. Если же значения
пар
Рис. 4
выражений Zl И Z2 ИЛИ Z3 и Z4 имеют одинаковые знаки, то отрезки не пересекаются.
Различные случаи расположения отрезков показаны на рисунке 4.
На этом рисунке отрезки с концами в точках И), (х; И) и (хг, И), К) пересекаются, отрезки с конца ми в точках (хг, И), (х; И) и (хз; уз), (хг, 1ј4) не пересекаются, а отрезки с концами в точках (хз; уз), (и; И) и (хг, У4) и (х5; Уб) имеют общую вершину. Последний случай можно считать частным случаем пересечения.
Алгоритм для определения, пересекаются ли два отрезка с концами в точках (хг, уј, (х; И) и (хз; уз), (Ч; Ш), будет следующим:
Р: = «истина»
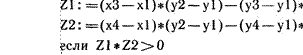 И: (хЗ —xl )*(у2
И: (хЗ —xl )*(у2
то р: = «ложь» все
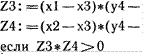 УЗ) —уЗ)*(х4
УЗ) —уЗ)*(х4![]()
УЗ) (Р— — хЗ)
то р : «ложь» все
Приведенный фрагмент алгоритма не учитывает
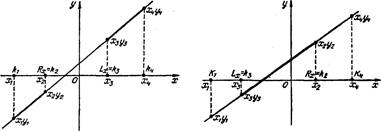
Рис. 5 Рис. 6
крайней ситуации, когда два отрезка лежат на одной прямой. В этом случае
![]()
На рисунке 5 отрезки, лежащие на одной прямой, не пересекаются, а на рисунке 6 — пересекаются.
Для того чтобы определить взаимное расположение таких
отрезков, поступим следующим образом. Обозначим kl =min И); ![]() ч); k3=min
(хз; И);
ч); k3=min
(хз; И); ![]() =тах (хз; д).
=тах (хз; д).
Здесь kl является левой, а Ь — правой точкой проекции первого отрезка (отрезка, заданного координатами (и; И), (х; У2)) на ось Ох. Аналогично Кз является левой, а К4 — правой точкой проекции второго отрезка (отрезка, заданного координатами (хз; уз), (х; на ось Ох. Аналогично ищем проекции на ось Оу.
|
|
6 |
|
|
|
Отрезки, лежащие на одной прямой, будут пересекаться
тогда, когда их проекции на каждую ось пересекаются. (Следует заметить, что
если проекции двух произвольных ![]() отрезков пересекаются, то это не значит,
что и сами отрезки пересекаются, что видно на рисунке 7.)
отрезков пересекаются, то это не значит,
что и сами отрезки пересекаются, что видно на рисунке 7.) ![]() Рис. 7 Для
определения взаимного расположения проекций на ось Ох воспользуемся следующим
фактом (см. рис. 5 и 6): координата левой точки пересечения проекций Lx равна
тах (КГ, Кз), т. е. максимальной из координат левых точек проекций. Рассуждая
аналогично для правых точек проекций, получим, что координата правой точки Rх
пересечения равна min (К; Щ). Для того чтобы отрезки пересекались, необходимо,
чтобы левая координата пересечения проекций была не больше правой координаты
пересечения отрезков (такой случай имеет место на рис. 5, когда Lx=x3, а ь),
Поэтому условием пересечения проекций является выполнение неравенства Lx<Rx
Рис. 7 Для
определения взаимного расположения проекций на ось Ох воспользуемся следующим
фактом (см. рис. 5 и 6): координата левой точки пересечения проекций Lx равна
тах (КГ, Кз), т. е. максимальной из координат левых точек проекций. Рассуждая
аналогично для правых точек проекций, получим, что координата правой точки Rх
пересечения равна min (К; Щ). Для того чтобы отрезки пересекались, необходимо,
чтобы левая координата пересечения проекций была не больше правой координаты
пересечения отрезков (такой случай имеет место на рис. 5, когда Lx=x3, а ь),
Поэтому условием пересечения проекций является выполнение неравенства Lx<Rx![]()
Аналогично можно вычислить величины Ly И Ry, взяв соответствующие проекции на ось Оу.
Следует отметить, что длина пересечения проекций в этом случае равна величине Rx— Lx (если Rx— Lx=O, то проекции имеют только общую точку).
1.4. Точка пересечения отрезков
Для определения места пересечения отрезков (если известно, что они пересекаются), достаточно определить точку пересечения прямых, на которых эти отрезки лежат.
Пусть А ![]() — уравнение прямой,
прохо
— уравнение прямой,
прохо![]() дящей через концевые точки первого
отрезка, а A2X-F + Вм+ С2=0 — уравнение прямой, проходящей через концевые точки
второго отрезка.
дящей через концевые точки первого
отрезка, а A2X-F + Вм+ С2=0 — уравнение прямой, проходящей через концевые точки
второго отрезка.
Тогда для определения точки пересечения отрезков достаточно решить систему уравнений
![]()
Домножив первое уравнение на 142, а второе ![]() получим
получим
![]()
Вычитаем из первого уравнения второе и находим значение у:
У![]()
Аналогично вычисляем значение х:
BlC2—B2Cl
![]()
Это справедливо в случае,
если 142 • Щ —АеВ2*0. Но мы уже знаем, что отрезки пересекаются и не лежат на
одной прямой, а это невозможно, если h12•Bl —А 1 , Щ![]()
Вопроеы для повторения
1. Как определить коэффициенты общего уравнения прямой, если известно уравнение прямой с угловым коэффициентом?
2. Каким может быть взаимное расположение отрезка и прямой?
З. Как определить, что отрезки параллельны?
4. Как определить взаимное расположение двух параллельных отрезков?
S 2. РАССТОЯНИЕ КА ПЛОСКОСТИ
2.1. Расстояние между точками. Расстояние от точки до прямой
![]() Расстояние между точками Ml (Ч; щ) и Ма (х; (32) на
плоскости (рис. 8) определяется по формуле
Расстояние между точками Ml (Ч; щ) и Ма (х; (32) на
плоскости (рис. 8) определяется по формуле
D
= (x.l — — У2)2 ![]()
Расстояние от точки до прямой на плоскости определяется как длина отрезка перпендикуляра, опущенного из точки на прямую. Уравнение вида
|
|
|
Рис. 8 Рис. 9
Ах ву С
![]()
![]() причем С (чего можно достигнуть изменением
знака выражения), называется нормальным уравнением прямой. Это уравнение
обладает тем свойством, что при подстановке координат произвольной точки в
выражение (Ах+Ву+ С)/Т получается значение, по абсолютной величине равное
расстоянию от точки до прямой (рис. 9).
причем С (чего можно достигнуть изменением
знака выражения), называется нормальным уравнением прямой. Это уравнение
обладает тем свойством, что при подстановке координат произвольной точки в
выражение (Ах+Ву+ С)/Т получается значение, по абсолютной величине равное
расстоянию от точки до прямой (рис. 9).
![]() Запишем алгоритм для определения расстояния от точки (хз;
уз) до прямой, проходящей через точки (хь щ)
Запишем алгоритм для определения расстояния от точки (хз;
уз) до прямой, проходящей через точки (хь щ)
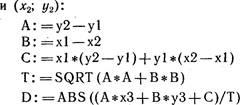
Рассмотрим пример. Пусть —0, —0, ь = З, И ![]() хз — — 1,
уз— 7. Тогда уравнение прямой, проходящей через точки (xt; щ) и (х; У2), будет
следующим:
хз — — 1,
уз— 7. Тогда уравнение прямой, проходящей через точки (xt; щ) и (х; У2), будет
следующим:
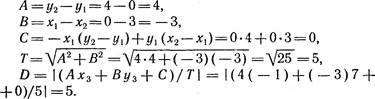
2.2. Расстояние между точкой и отрезком
Для определения расстояния между точкой и отрезком необходимо выяснить, пересекает ли перпендикуляр, опущенный из данной точки на прямую, проходящую через концы отрезка, сам отрезок. Если перпендикуляр пересекает отрезок, то расстояние между точкой и отрезком равно расстоянию между точкой и прямой, проходящей через отрезок. (Эту задачу вы уже умеете решать.) Если перпендикуляр не пересекает отрезок, то расстояние между точкой и отрезком равно минимальному из расстояний между точкой и одним из концов отрезка. Для определения взаимного расположения отрезка и перпендикуляра поступим следующим образом.
Рассмотрим треугольник, образованный тремя точками, две из которых у) и (х; И) являются концами данного отрезка, а третья — данная точка с координатами (хз; уз) (рис. l()). Конечно, может оказаться, что все точки лежат на одной прямой и такого треугольника не существует. В этом случае, однако, мы будем полагать, что треугольник существует, правда он вырожденный (особый). В вырожденном треугольнике вершины могут лежать на одной прямой (см. рис. 10, а).
Более того, мы будем полагать, что данный отрезок является основанием рассматриваемого треугольника (см. рис. 10, б, в).
При таких предположениях для решения исходной задачи нам достаточно определить, является ли один из углов при основании тупым. Действительно, если один из
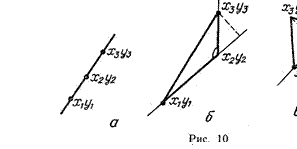
углов при основании тупой, то перпендикуляр, опущенный из вершины, соответствующей исходной точке, не попадает на основание (отрезок). Если угол не тупой, то перпендикуляр, опущенный из вершины, соответствующей исходной точке, попадает на основание (отрезок).
Для решения последней задачи воспользуемся следующим
свойством. Пусть а, Ь, с — длины сторон треугольника, причем с— длина
основания. Тогда треугольник является тупоугольным при основании, если ![]() a2>b2+c2
или а2+ 8
a2>b2+c2
или а2+ 8![]()
Поэтому, вычислив значения квадратов длин сторон, нетрудно определить, пересекает ли перпендикуляр, опущенный из точки (хз; уз) на прямую, отрезок с концами в точках Щ) и (х; И). И если не пересекает, то расстояние от точки до отрезка равно минимуму из величин а, Ь. Если же пересекает, то необходимо воспользоваться формулой расстояния от точки до прямой.
Вопросы для повторения
1. Как определить расстояние между двумя точками?
2. Чему равно расстояние между точкой и прямой?
З. Как определяется расстояние между отрезками?
S З. МНОГОУГОЛЬНИКИ
3.1. Виды многоугольников
![]() Ап и соединяющих их отрезков AlA2, А2Аз,
Ап и соединяющих их отрезков AlA2, А2Аз, ![]() Ап д
п (рис. 11, а). Точки называются вершинами ломаной, а отрезки — звеньялш.
Наиболее распространенным способом задания ломаной является использование
таблицы, элементы которой соответствуют координатам вершин ломаной в порядке ее
обхода из одного конца в другой. Длиной ломаной называется сумма длин ее
звеньев.
Ап д
п (рис. 11, а). Точки называются вершинами ломаной, а отрезки — звеньялш.
Наиболее распространенным способом задания ломаной является использование
таблицы, элементы которой соответствуют координатам вершин ломаной в порядке ее
обхода из одного конца в другой. Длиной ломаной называется сумма длин ее
звеньев.
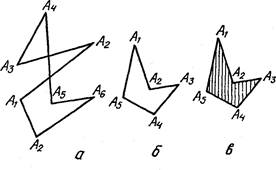
Рис. ll
Многоугольником называется замкнутая ломаная линия без самопересечений (рис. l l , б).
плоским многоугольником называется конечная часть плоскости, ограниченная многоугольником (рис.
Обход плоского многоугольника называется положительным, если при обходе область расположена по левую руку, и отрицательным, если область остается по правую руку.
Расстояние между фигурами на плоскости определяется как длина минимального отрезка, один конец которого принадлежит одной фигуре, а второй конец — другой фигуре.
3.2. Выпуклость многоугольников
Многоугольник является выпуклым, если для каждой прямой,
проходящей через любую его сторону, все остальные вершины лежат в одной
полуплоскости относительно прямой. Проверим для каждой прямой, проходящей через
вершины (хг, И) и (х; И), (х; И) и (хз; уз), ![]() (хп_1,• уп_1) И (хп;
УП), (Х; ут) И (ХВ И), взаимное расположение вершин многоугольника. Если они
каждый раз расположены в одной полуплоскости относительно проведенной прямой,
то многоугольник выпуклый. Если же
(хп_1,• уп_1) И (хп;
УП), (Х; ут) И (ХВ И), взаимное расположение вершин многоугольника. Если они
каждый раз расположены в одной полуплоскости относительно проведенной прямой,
то многоугольник выпуклый. Если же
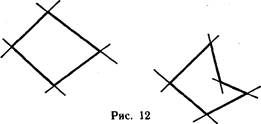
![]() найдется прямая,
проходящая через одну из сторон, и пара вершин многоугольника, лежащих по
разные стороны относительно проведенной прямой, то многоугольник не является
выпуклым. Случаи выпуклого и невыпуклого многоугольников изображены на рисунке
l2. Можно заметить, что для каждой прямой, проходящей через вершины (Ч; У}) и
И), (Ч, И) и (хз; уз),
найдется прямая,
проходящая через одну из сторон, и пара вершин многоугольника, лежащих по
разные стороны относительно проведенной прямой, то многоугольник не является
выпуклым. Случаи выпуклого и невыпуклого многоугольников изображены на рисунке
l2. Можно заметить, что для каждой прямой, проходящей через вершины (Ч; У}) и
И), (Ч, И) и (хз; уз), ![]() (xn_f, yn_l) и (х; Л), (х; ут) и И),
достаточно ограничиться определением взаимного расположения вершин
многоугольника (х; УП) и (хз; уз), И) и (хг, И), ..., (хп_; уп_2) и (ХГ, И),
yn_l) и (Х; У2) соответственно. Если они каждый раз расположены в одной
полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если
же найдется прямая и пара вершин многоугольника, лежащих по разные стороны
относительно проведенной прямой, то многоугольник не является выпуклым. Поэтому
для определения, является ли многоугольник выпуклым, достаточно воспользоваться
алгоритмом (1.6).
(xn_f, yn_l) и (х; Л), (х; ут) и И),
достаточно ограничиться определением взаимного расположения вершин
многоугольника (х; УП) и (хз; уз), И) и (хг, И), ..., (хп_; уп_2) и (ХГ, И),
yn_l) и (Х; У2) соответственно. Если они каждый раз расположены в одной
полуплоскости относительно проведенной прямой, то многоугольник выпуклый. Если
же найдется прямая и пара вершин многоугольника, лежащих по разные стороны
относительно проведенной прямой, то многоугольник не является выпуклым. Поэтому
для определения, является ли многоугольник выпуклым, достаточно воспользоваться
алгоритмом (1.6).

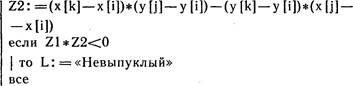
кц
Вопросы для повторения
![]() 1. Какие бывают обходы многоугольника?
1. Какие бывают обходы многоугольника?
2. Какой многоугольник называется ВЫПУКЛЫМ?
S 4. ПЛОЩАДИ ФИГУР
4.1. Площадь треугольника
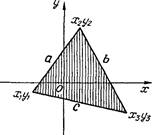
Для вычисления площади треугольника (рис. 13) известна
формула Герона: ![]()
![]() S p(p—a)(p—b)(p—c), где а,
Ь, с — длины сторон треугольника, а р — его полупериметр, т. е.
S p(p—a)(p—b)(p—c), где а,
Ь, с — длины сторон треугольника, а р — его полупериметр, т. е.![]()
Так как при заданных координатах вершин треугольника можно вычислить длины его сторон, то алгоритм поиска площади треугольника сводится к поиску длин сторон и использованию формулы Герона.
![]()
 Однако такой метод вычисления площади имеет один
существенный недостаток: необходимо выполнение операции нахождения квадратного
корня из числа. При выполнении этой операции часто происходит потеря точности,
что может привести к получению не совсем точного результата. Поэтому, чтобы
избежать возможных ошибок, в дальнейшем будут использоваться другие фор-
Однако такой метод вычисления площади имеет один
существенный недостаток: необходимо выполнение операции нахождения квадратного
корня из числа. При выполнении этой операции часто происходит потеря точности,
что может привести к получению не совсем точного результата. Поэтому, чтобы
избежать возможных ошибок, в дальнейшем будут использоваться другие фор-
мулы. Рис. 13
 4.2. Площадь прямоугольника
4.2. Площадь прямоугольника
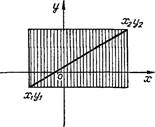
Мы будем рассматривать прямоугольники, стороны которых параллельны осям координат (рис. 14).
В этом случае прямоугольник может быть определен одной из своих диагоналей. Это значит, что пара точек на пло-
Рис. 14
скости с координатами (Хё, И) и (хы, И), соответствующая концам диагонали, однозначно определяет расположение и размер прямоугольника. Такое задание более удобно вместо описания прямоугольника посредством последовательности вершин в порядке обхода. Кроме того, при таком задании легко вычислить площадь прямоугольника по формуле
![]()
где ![]() — длина проекции
прямоугольника на ось Ох (длина стороны, параллельной оси Ох), а
— длина проекции
прямоугольника на ось Ох (длина стороны, параллельной оси Ох), а ![]() длина
проекции прямоугольника на ось Оу (длина стороны, параллельной оси Оу).
длина
проекции прямоугольника на ось Оу (длина стороны, параллельной оси Оу).
4.3. Площадь трапеции
Мы будем рассматривать трапеции, основания которых параллельны оси Оу, одна из боковых сторон ле-
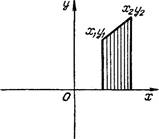 жит на оси Ох, а
другая расположена выше оси Ох (рис. 15).
жит на оси Ох, а
другая расположена выше оси Ох (рис. 15).
В этом случае трапеция может быть определена парой точек (хг, Щ) и (х; И), соответствующих вершинам трапеции, не лежащим на оси Ох. При таком задании легко вычислить площадь трапеции по
Рис. 15 формуле
1х2 — % l(Y2+Yt) 2
где ![]() — высота трапеции, а и
— длины ее оснований.
— высота трапеции, а и
— длины ее оснований.![]()
4.4. Площадь плоского многоугольника
Сначала мы рассмотрим плоские многоугольники, расположенные выше оси Ох.
Традиционно при подсчете площади произвольного многоугольника его разбивают на треугольники и находят площадь каждого из них. Сумма площадей этих треугольников равна площади данного многоугольника.
Однако при этом возникает вопрос, каким образом делать это разбиение, если многоугольник задан координатами ломаной в порядке ее обхода и при этом не является выпуклым.
Более рациональным способом нахождения площади многоугольника
является его представление в виде комбинации трапеций. При этом считается, что
если рассматривается трапеция, у которой <х2, то значение ее площади берется
со знаком «+» (рис. l6, а), а если х, >х2, то значение ее площади берется со
знаком « ![]() (рис. 16, б).
(рис. 16, б).
При вычислении значения площади используется формула
а
|
|
|
||||||
Рис. 16
![]()
2
Используя такой подход, формула для подсчета площади многоугольника, определяемого ломаной с координатами вершин (хг, у), (Ч, И), . . . , ( Хп—:; yn—l)' уп) примет следующий вид:
![]() ( хя
—х ,) (У2+У1) (хз
—Х2) (Уз+У2)
( хя
—х ,) (У2+У1) (хз
—Х2) (Уз+У2)
2 2 или
![]()
При и эти формулы могут быть использованы для вычисления площадей треугольников и четырехугольников соответственно.
При этом совершенно безразлично, выпуклый многоугольник или нет (рис. 17). Более того, вычисление площади требует выполнения только операций сложения, вычитания, умножения и одной операции деления.
|
|
|
|
|
|
Г |
|
При более детальном изучении оказывается, что приведенная выше формула может использоваться для произвольных точек на плоскости, т. е. точки могут располагаться и ниже оси Ох. Правда, при этом необходимо предварительно осуществить преобразование координат по формуле
![]() тЈП'
тЈП'
где ymin — минимальное значение у
координаты для вершин многоугольника в исход![]() ной системе координат.
Такое преобразование соответствует параллельному переносу мноРис. гоугольника
параллельно оси
ной системе координат.
Такое преобразование соответствует параллельному переносу мноРис. гоугольника
параллельно оси
Оу и гарантирует, что в новой системе координат ни одна вершина многоугольника не будет расположена ниже оси Ох.
Алгоритм для определения площади плоского многоугольника, заданного координатами его вершин в порядке их обхода по контуру, будет таким.
![]() (Внимание! Здесь и в дальнейшем мы будем предполагать, что
обход многоугольника задается n+•l вершиной, причем (п+ 1)-я вершина совпадает
с первой вершиной обхода.) ymin: =
(Внимание! Здесь и в дальнейшем мы будем предполагать, что
обход многоугольника задается n+•l вершиной, причем (п+ 1)-я вершина совпадает
с первой вершиной обхода.) ymin: = ![]() нц для К от 2 до п если yrnin>y [К] то
ymin:
нц для К от 2 до п если yrnin>y [К] то
ymin: ![]() все
все
нц для К от до п +1 ![]()
![]() У
[К] — ymin кц
У
[К] — ymin кц
нц для К от I до п
![]()
кц
Вопросы для повторения
1. Как можно вычислить ппощвдь треугольника, если известны координаты его вершин?
2. Какие преобразования можно сделать, чтобы многоугольник лежал выше оси Ох?
З. Какой способ вычисления площади треугольника более эффективен: формула Герона или общая формула?
S 5. ВЗАИМНОЕ РАСПОЛОЖЕНИЕ ФИГУР
НА ПЛОСКОСТИ
5.1. Взаимное расположение многоугольника и точки
Существует много способов определения взаимного расположения многоугольника и точки. Рассмотрим один из наиболее употребительных способов, который называется методом сканирующей прямой, и основывается на следующем.
![]() Находясь в данной точке (хо; До), мы
начинаем двигаться в одном направлении (это может быть любое направление,
например, параллельно оси Ох), подсчитывая при этом количество пересеченных
сторон многоугольника. Движение заканчивается тогда, когда мы уйдем достаточно
далеко, и ни одна сторона многоугольника уже не сможет встретиться на нашем
пути. Оказывается, что если при нашем движении было пересечено нечетное число
сторон многоугольника, то исходная точка лежит внутри многоугольника (рис. 18,
а), а если было пересечено четное число сторон, то точка лежит снаружи (рис. 18
6, в).
Находясь в данной точке (хо; До), мы
начинаем двигаться в одном направлении (это может быть любое направление,
например, параллельно оси Ох), подсчитывая при этом количество пересеченных
сторон многоугольника. Движение заканчивается тогда, когда мы уйдем достаточно
далеко, и ни одна сторона многоугольника уже не сможет встретиться на нашем
пути. Оказывается, что если при нашем движении было пересечено нечетное число
сторон многоугольника, то исходная точка лежит внутри многоугольника (рис. 18,
а), а если было пересечено четное число сторон, то точка лежит снаружи (рис. 18
6, в).
Маршрут нашего движения может быть представлен в виде отрезка, координаты одной концевой точки которого равны координатам исходной точки, а одна из координат другой концевой точки больше (или меньше) любой соответствующей координаты вершин многоугольника.
В этом случае задача взаимного расположения многоугольника и точки сводится к подсчету числа пересечения полученного отрезка и сторон многоугольника. Другая координата может быть любой. Обычно ее берут равной соответствующей координате исходной точки. В этом случае маршрут движения происходит вдоль одной из осей координат.
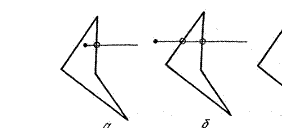
![]() Рис. 18
Рис. 18
![]() В этом случае задача взаимного
расположения многоугольника и точки сводится к подсчету числа пересечений
полученного отрезка и сторон многоугольника. В массивах Х и У хранятся
координаты вершин многоугольника в порядке обхода, х у [0] — координаты
исходной точки.
В этом случае задача взаимного
расположения многоугольника и точки сводится к подсчету числа пересечений
полученного отрезка и сторон многоугольника. В массивах Х и У хранятся
координаты вершин многоугольника в порядке обхода, х у [0] — координаты
исходной точки.
xmin: = ![]() нц для К от 2 до п
если xmin>x [К] то xmin:
нц для К от 2 до п
если xmin>x [К] то xmin:![]()
все кц
![]()
нц для i от 1 до п 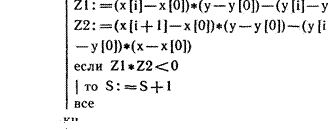 х [01)
х [01)
L: = «внутри» если mod (S, ![]() I
то L: ==«вне» все
I
то L: ==«вне» все
Такой подход требует особого анализа случаев, когда полученный отрезок пересекает сторону многоугојљника в концевой точке.
Если отрезок пересекает одну из вершин многоугольника (например, Щ), то может быть 2 случая (рис. l9):
1) Обе стороны многоугольника, входящие в вершину Щ, лежат по одну сторону от отрезка (рис. 19, а). Количество пересечений можно считать равным 2 (или 0);
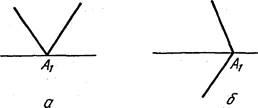
Рис. 19
2) стороны многоугольника, входящие в вершину А 1 , лежат по разные стороны отрезка (рис. 19, б). Число пересечений примем равным 1.
Для проверки, по разные или по одну. сторону от прямой лежат стороны многоугольника, можно использовать алгоритм (1.3).
Если отрезок проходит по стороне, то число пересечений будем считать равным 2.
5.2. Взаимное расположение многоугольников
Возможны З варианта взаимного расположения многоугольников:
они могут пересекаться (рис. 20, а), лежать один внутри другого (рис. 20, б)
или располагаться каждый вне другого (рис. 20, в). ![]()
Определение взаимного расположения многоугольников, заданных обходами своих вершин, будет проводиться в два этапа.
Первый этап. Для того чтобы определить взаимное расположение многоугольников, следует проверить взаим-
![]() В д ьа
В д ьа![]()
Рис. 20 ![]()
ное расположение сторон многоугольников. Если две стороны разных многоугольников пересекаются, то и многоугольники пересекаются. Поэтому для определения возможного пересечения сторон многоугольников можно воспользоваться алгоритмом (1.4). Если найдется пара сторон из разных многоугольников, которые пересекаются, то взаимное положение многоугольников определено.
Если оказалось, что в многоугольниках нет взаимно пересекающихся сторон, то переходим ко второму этапу.
Второй этап. Устанавливаем взаимное расположение вершины одного из многоугольников и другого многоугольника. Если оказалось, что вершина одного из многоугольников лежит внутри другого многоугольника, то один из многоугольников лежит внутри другого. Следовательно, взаимное расположение многоугольников установлено.
Пусть для каждого из многоугольников его вершина лежит вне другого многоугольника. В этом случае остается единственно возможное решение: каждый многоугольник лежит вне другого.
Вопросы для повторения
1. Как определить взаимное расположение многоугольника и точки?
2. Зависит ли способ определения взаимного расположения многоугольника и точки от выпуклости многоугольника? З. Назовите возможные расположения двух треугольников.
ЗАДАЧИ ДЛЯ ПОВТОРЕНИЯ
1. Даны три числа а, Ь, с. Определить, существует ли треугольник с такими длинами сторон.
2. Даны четыре числа а, Ь, с, d. Определить, существует ли четырехугольник с такими длинами сторон.
З. Найти взаимное расположение окружности радиуса R с центром в точке (хо; И) и точки А с координатами
![]()
4. Найти взаимное расположение двух окружностей
радиуса Rl и R2 с центрами в точках (Xl; у, ) и (х; И) соответственно.
5. Найти
взаимное расположение окружности радиу![]() са R с центром в точке (хо; И) и прямой,
проходящей через точки с координатами (Хё, И) и (х; И).
са R с центром в точке (хо; И) и прямой,
проходящей через точки с координатами (Хё, И) и (х; И). ![]()
6. Определить количество точек с целочисленными координатами, лежащих внутри окружности радиуса R с центром в точке (хо; до).
7. Найти координаты точек пересечения двух окружностей радиусов R1 и R2 с центрами в точках (ю; щ) и (х; !l2) соответственно.
![]() 8. Найти координаты точки, симметричной
данной точке М с координатами (Xl,' щ) относительно прямой Ах + Ву+С=0.
8. Найти координаты точки, симметричной
данной точке М с координатами (Xl,' щ) относительно прямой Ах + Ву+С=0.
9. Даны
две точки Ml (xt; у), МА х; У2) и прямая Ах+Ву+С=О. Найти на этой прямой такую
точку Мо (хо; И), чтобы суммарное расстояние от нее до двух данных точек было
минимально.![]()
10. Даны три точки с координатами ( „Ч; И), (х; И), (хз; уз), которые являются вершинами некоторого прямоугольника. Найти координаты четвертой вершины.
11. Даны координаты
вершин четырехугольника (хк, щ), (х; И), (хз; уз), (х; И). Определить, выпуклый
ли ![]() четырехугольник.
четырехугольник.
12. Даны координаты вершин четырехугольника (хк, И), (х; И), (хз; уз), (х; И). Определить, является ли четырехугольник: а) ромбом; б) квадратом; в) трапецией.
13. Даны координаты двух вершин ( и (х; И) некоторого квадрата. Найти возможные координаты других его вершин.
14. ![]() Даны
координаты двух вершин И) и (х; У2) некоторого квадрата, расположенных по
диагонали, и точка (хз; уз). Определить, лежит ли точка внутри квадрата.
Даны
координаты двух вершин И) и (х; У2) некоторого квадрата, расположенных по
диагонали, и точка (хз; уз). Определить, лежит ли точка внутри квадрата.
15. Даны координаты (хв
И), (х; И), (хз; уз) вершин треугольника. Найти координаты точки пересечения
его ![]() медиан.
медиан.
28
![]() 16. Даны координаты (щ; у), (ь; ф), (хз;
уз) вершин треугольника. Найти длины его высот.
16. Даны координаты (щ; у), (ь; ф), (хз;
уз) вершин треугольника. Найти длины его высот.
17. Определить коэффициенты уравнения прямой, параллельной данной прямой, определяемой уравнением Ах+Ву+С=0 и проходящей через точку с координатами (хо; Уо)•
![]() 18. Определить коэффициенты уравнения
прямой, перпендикулярной данной прямой, определяемой уравнением Ах+Ву+С=О и
проходящей через точку с координатами (хо; И).
18. Определить коэффициенты уравнения
прямой, перпендикулярной данной прямой, определяемой уравнением Ах+Ву+С=О и
проходящей через точку с координатами (хо; И).
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ
1. Определить, пересекаются ли прямая y=kx+b и отрезок с концами (хь Yl)' (х; У2).
2. Определить, принадлежит ли точка А (х; у) отрезку с концевыми точками B(xr•, У!) и С (х; И).
З. а) Выпуклый многоугольник задается координатами своих вершин при его обходе по часовой или против часовой стрелки. Контур многоугольника не имеет самопересечений. Определить направление обхода.
б) Определить направление обхода в случае невыпуклого многоугольника.
4. На плоскости заданы п отрезков координатами концевых
точек. Концы отрезков задаются двумя парами координат (Xl [i]; [i]), (х2 ![]() (концы
принадлежат отрезку). Найти прямую, имеющую общие точки с максимальным числом
отрезков, и напечатать в порядке возрастания номера тех отрезков, которые эта
прямая пересекает.
(концы
принадлежат отрезку). Найти прямую, имеющую общие точки с максимальным числом
отрезков, и напечатать в порядке возрастания номера тех отрезков, которые эта
прямая пересекает.
![]() 5. N точек на плоскости заданы своими
координатами. Найти такой минимальный по площади выпуклый многоугольник, что
все N точек лежат либо внутри этого многоугольника, либо на его границе (такой
выпуклый многоугольник называется выпуклой оболочкой).
5. N точек на плоскости заданы своими
координатами. Найти такой минимальный по площади выпуклый многоугольник, что
все N точек лежат либо внутри этого многоугольника, либо на его границе (такой
выпуклый многоугольник называется выпуклой оболочкой).
![]() 6. На плоскости заданы своими
координатами К точек. Определить, можно ли построить такой ВЫПУКЛЫЙ
многоугольник, что каждая точка принадлежит некоторой стороне.
6. На плоскости заданы своими
координатами К точек. Определить, можно ли построить такой ВЫПУКЛЫЙ
многоугольник, что каждая точка принадлежит некоторой стороне.
7.
N точек на плоскости заданы своими координатами. Найти порядок, в
котором можно соединить эти ![]() точки, чтобы получился
точки, чтобы получился![]()
8. Представьте себе, что в тетрадке Вы закрасили на листе какое-то количество клеточек и получили клеточную фигуру. Сколько осей симметрии имеет заданная клеточная фигура?
Заданы: Ni— размер фигуры по вертикали, Nj — размер фигуры по
горизонтали (Ni< 101; N.<81) и сама фигура в виде Ni строк из пробелов и
звездочек по Nj символов в каждой строке.![]()
Звездочка соответствует закрашенной
клеточке.![]()
Пример 1.
2 4 (размер фигуры по вертикали и горизонтали)
![]()
Фигура имеет ось симметрии.
Пример 2.
З 5 (размер фигуры по вертикали и горизонтали)
![]()
Фигура имеет 0 осей симметрии.
9. Прямоугольник ABCD задан координатами своих вершин. На противоположных сторонах АВ и CD заданы последовательности Rl и R2 из N точек разбиения, а на сторонах ВС и AD — R3 и R 4 из М точек разбиения. Нумерация элементов последовательностей R 1 и R2 начинается соответственно от точек А и D, а R3 и R 4 — от В и Њ Соединив отрезками точки с одинаковыми номерами в разбиениях Rl и R2, а затем в разбиениях R3 и R 4, получим разбиение Q прямоугольника ABCD на множество четырехугольников.
Найти четырехугольник разбиения Q с наибольшей площадью при условии, что отрезки, соединяющие точки разбиений R1 и R2 параллельны стороне AD. Последовательности Rl, R2, R3 и R4 задаются как массивы из длин отрезков разбиения соответствующих сторон прямоугольника.
10. На прямой задано N точек с координатами х], х2, . .. , XN. Найти такую точку Z, сумма расстояний от которой до данных точек минимальна.
11. Пусть
через административный район проходит по прямой железная дорога. На ней надо
построить станцию так, чтобы расстояние от нее до самой дальней деревни было бы
минимальным. Написать программу. 12. На плоскости задано N точек с координатами
![]() (х; ул). Написать программу, которая из
этих точек выделяет вершины квадрата, содержащего максимальное число заданных
точек. (Предполагается, что точки, расположенные на сторонах квадрата,
принадлежат ему.)
(х; ул). Написать программу, которая из
этих точек выделяет вершины квадрата, содержащего максимальное число заданных
точек. (Предполагается, что точки, расположенные на сторонах квадрата,
принадлежат ему.)
13. ![]() На
плоскости задано множество из N прямоугольников, стороны которых параллельны
осям координат, при этом каждый прямоугольник задается координатами левой
нижней и правой верхней его вершин. Составить алгоритм определения наибольшего
натурального числа К, для которого существует точка плоскости, принадлежащая
одновременно К прямоугольникам.
На
плоскости задано множество из N прямоугольников, стороны которых параллельны
осям координат, при этом каждый прямоугольник задается координатами левой
нижней и правой верхней его вершин. Составить алгоритм определения наибольшего
натурального числа К, для которого существует точка плоскости, принадлежащая
одновременно К прямоугольникам.
П ри меч а н не. Эффективным считается алгоритм, число действий которого пропорционально N 2.
14. На
квадратном торте N свечей. Можно ли одним прямолинейным разрезом разделить его
на две равные по площади части, одна из которых не содержала бы ни одной свечи?
Свечи будем считать точками, у которых известны их целочисленные координаты (хв
щ), ![]() (хм, YN). Начало координат — в центре
торта. Разрез не может проходить через свечу.
(хм, YN). Начало координат — в центре
торта. Разрез не может проходить через свечу.
15. Даны
![]() прямоугольников,
для которых предполагается, что:
прямоугольников,
для которых предполагается, что:
а) стороны любого прямоугольника параллельны ко-
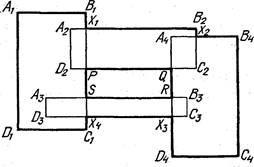
Рис. 21![]()
ординатным осям и прямоугольник задается
концами ![]() одной из диагоналей;
одной из диагоналей;
б) каждый прямоугольник имеет общие внутренние ![]() точки с хотя
бы одним из остальных и не имеет общих вершин, сторон или частей сторон ни с
одним из остальных прямоугольников.
точки с хотя
бы одним из остальных и не имеет общих вершин, сторон или частей сторон ни с
одним из остальных прямоугольников. ![]()
Составить программу, которая даст возможность: 1) Определить внешний контур фигуры Е, являющейся объединением прямоугольников (рис. 21).
2) Определить, содержит ли фигура F «дырки», т. е. замкнутые фигуры, которые ей не принадлежат.
З) Разложить фигуру F на наименьшее возможное число
непересекающихся прямоугольников, которые могут иметь общие стороны или части
сторон, а их объединение дает фигуру F. ![]()
4) Вычислить периметр и площадь фигуры F.
Внешний контур объединения пря»моугольников AiBiCiDi, i—l, 2, З, 4, есть APPXXD 1 4 3 4 4 4 2 2 lСВХВ Х Щ; фигура F содержит единственную «дырку» PQRS.
П р и м е ч а н и е. Задачи З) и 4) решаются только для фигур, не содержащих «дырок».
16. Очертание города. Необходимо написать программу, которая должна помочь архитектору в рисовании очертания города. Город задается расположением зданий и рассматривается как двумерный; все здания
32
Рис. 22
в нем — прямоугольники, основания которых лежат на одной прямой (город построен на равнине). Здания задаются тройкой чисел (Ц, Hi, Ri), где Li И Ri — координаты левой и правой стен здания i, а Ц— высота этого здания. На рисунке 22 здания описываются тройками (0, 11, 5), (2, 6, 7), (3, 13, 10), (12, 7, 16), (14, з, 25), (20, 18, 22),
(23, 13, 30), (24, 4, 29), а контур, показанный на рисунке
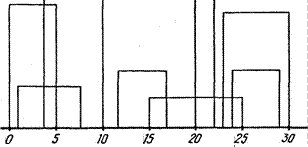 |
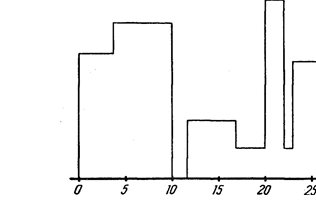
Рис. 23
2 Информатика, 8—9 КЛ. 33
Ввод представляет собой последовательность троек, задающих дома. Все координаты есть целые числа меньше 10000. Во входном файле минимум одно и максимум 50 зданий. Каждая тройка, обозначающая здание, находится в отдельной строке во входном файле. Все целые числа в тройке разделены одним или несколькими пробелами. Тройки отсортированы по Li, т. е. по левой х-координате здания, таким образом, здание с самой маленькой левой х-координатой является первым во входном файле.
Вывод будет состоять из вектора, описывающего очертание, как показано в примере выше. В векторе очертание (01, 02, Ч, СУП— 2' оп— vn), Vi означает горизонтальную линию (высоту), когда i — четное число, и вертикальную линию (х-координату), когда i— нечетное. Вектор очертания будет определять маршрут, пройденный, к примеру, жуком, начавшим с минимальной х-координаты и путешествующим по всем вертикальным и горизонтальным линиям, определяющим контур. Последний элемент в векторе линии контура будет О.
17. Нижняя левая и
верхняя правая вершины прямоугольника А имеют координаты (О; О) и (У; У)
соответственно. Множество S из N точек задается парами координат (х; И), ![]() Найти
такой прямоугольник G максимальной площади, что его стороны параллельны
сторонам А, G полностью лежит в А (G и А могут иметь общие граничные точки) и
ни одна точка S не лежит внутри G (но может лежать на его стороне). Напечатать
величину площади G и координаты нижней левой и верхней правой вершин этого
прямоугольника. Если таких прямоугольников несколько, то вывести информацию по
каждому.
Найти
такой прямоугольник G максимальной площади, что его стороны параллельны
сторонам А, G полностью лежит в А (G и А могут иметь общие граничные точки) и
ни одна точка S не лежит внутри G (но может лежать на его стороне). Напечатать
величину площади G и координаты нижней левой и верхней правой вершин этого
прямоугольника. Если таких прямоугольников несколько, то вывести информацию по
каждому.
П р и м е ч а н и е. Во множестве S никакие две точки не лежат на одной прямой, параллельной стороне А.
34
18. 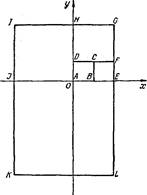 В первом
квадрате координатной системы Оху нарисован первый квадрат — ABCD, длина
стороны которого равна
В первом
квадрате координатной системы Оху нарисован первый квадрат — ABCD, длина
стороны которого равна ![]() и вершина А находится в начале координат.
Потом нарисованы: второй квадрат BEFC, третий — DFGH, четвертый — JAHI, пятый —
kLEJ и так далее по спирали (рис. 24). Написать программу, которая для
введенных целых чисел х и у
и вершина А находится в начале координат.
Потом нарисованы: второй квадрат BEFC, третий — DFGH, четвертый — JAHI, пятый —
kLEJ и так далее по спирали (рис. 24). Написать программу, которая для
введенных целых чисел х и у
Рис. 24
определяет и выводит номер квадрата, которому принадле-
жит точка Р (х; у). Если точка Р лежит на сторонах квадратов или в вершинах, то будем считать, что она принадлежит квадрату с наименьшим номером из возможных.
![]() Примеры. результат
Примеры. результат
2 2
![]() 4
4
13 2![]()
19. На плоскости заданы своими координатами N различных точек. Найти уравнение прямой, делящей это множество точек на два подмножества с одинаковым количеством элементов.
20. Найти пересечение и объединение двух выпуклых многоугольников. Многоугольники задаются координатами вершин в порядке обхода по контуру.
21. ![]() на плоскости
задается координатами вершин в порядке их обхода по контуру. Для точки Z (х; у)
найти минимальное расстояние до контура
на плоскости
задается координатами вершин в порядке их обхода по контуру. Для точки Z (х; у)
найти минимальное расстояние до контура
![]()
22. На плоскости своими
координатами задаются N точек. Матрица C[l..N, l..N] задается следующим
образом: ![]() в случае, если вершины i и ј соединены
отрезком, и 0, если не соединены. Известно, что любая вершина соединена, по
крайней мере, с двумя другими и что отрезки пересекаются только в концевых
точках.
в случае, если вершины i и ј соединены
отрезком, и 0, если не соединены. Известно, что любая вершина соединена, по
крайней мере, с двумя другими и что отрезки пересекаются только в концевых
точках. ![]() Таким образом, вся плоскость разбивается
на множество многоугольников. Задана точка Z (х; у). Найти минимальный по
площади многоугольник, содержащий Z, или выдать сообщение, что такого не
существует. Если Z принадлежит какому-то отрезку, то выдать его концевые точки;
если Z лежит в многоугольнике, то выдать его вершины в порядке обхода по
контуру.
Таким образом, вся плоскость разбивается
на множество многоугольников. Задана точка Z (х; у). Найти минимальный по
площади многоугольник, содержащий Z, или выдать сообщение, что такого не
существует. Если Z принадлежит какому-то отрезку, то выдать его концевые точки;
если Z лежит в многоугольнике, то выдать его вершины в порядке обхода по
контуру.
23. Будем называть два многоугольника подобными, если существует взаимно однозначное отображение сторон этих двух фигур такое, что соответствующие стороны пропорциональны с коэффициентом пропорциональности К, а углы, образованные двумя соответствующими сторонами, равны. Определить, подобны ли два многоугольника. Многоугольники задаются на плоскости координатами вершин контуров. Вершины в контуре перечисляются в порядке обхода против часовой стрелки.
Пр им е ч а н и е. Так как все вычисления на ЭВМ проводятся с ограниченной точностью, то считать, что две величины равны, если они совпадают с точностью до двух знаков после запятой.
24. Заданы натуральное
число N и две последовательности целых чисел (щ, щ, . . . , ат.4) и (bl, b2, . ![]() Заданы
также два числа хо и % , xo<Xl.
Заданы
также два числа хо и % , xo<Xl.
а) Найти числа to, , [р, p < N, такие, что хо = и указать
для каждого отрезка 1', tj], 1 такое число К, 1 ![]() что для всех i, и для
всех х из [tI tj] справедливо неравенство Ц.
что для всех i, и для
всех х из [tI tj] справедливо неравенство Ц.
![]() б) Найти числа so,
s1, такие, что хо = И указать ДЛЯ каждого отрезка такую перестановку (il, i2,
... , iN) чисел
б) Найти числа so,
s1, такие, что хо = И указать ДЛЯ каждого отрезка такую перестановку (il, i2,
... , iN) чисел
![]() N, что для всех х из [s У.]
справедливо неравенство ai •x+bi •x+b. .x+biN, и для всех отрезков
соответствующие перестановки различны.
N, что для всех х из [s У.]
справедливо неравенство ai •x+bi •x+b. .x+biN, и для всех отрезков
соответствующие перестановки различны.
25. В правильном п-угольнике провели несколько диагоналей, причем никакие три не пересекаются в одной точке. На сколько частей диагонали разбили п-угольник? Диагонали заданы номерами вершин п-угольника, которые они соединяют, все вершины перенумерованы по порядку числами 1 п.
26. Круг разрезан
самонепересекающейся ![]() координаты вершин которой заданы парами
натуральных чисел (хв щ), . . . , (хм, УК). Первая и последняя вершины лежат на
границе круга, а остальные — внутри него. Определить, можно ли разъединить две
получившиеся части круга (выход из плоскости и повороты разнимаемых частей не
допускаются).
координаты вершин которой заданы парами
натуральных чисел (хв щ), . . . , (хм, УК). Первая и последняя вершины лежат на
границе круга, а остальные — внутри него. Определить, можно ли разъединить две
получившиеся части круга (выход из плоскости и повороты разнимаемых частей не
допускаются).
27. На местности,
представляющей собой идеально ровную поверхность, стоит высокий забор. План
забора — замкнутая ломаная без самопересечений, которая задается N парами
координат своих вершин в порядке обхода ограничиваемой забором области против
часовой стрелки. Вершины пронумерованы от 1 до N, ![]() 100. В точке (х; у)
стоит человек ((х; у) не может лежать на ломаной). Считая, ч го каждому звену
ломаной ставится в соответствие пара номеров концевых вершин, указать, какие
звенья человек увидит полностью или частично, а какие — вообще не увидит. Если
при взгляде звено видно как точка или как пара точек, то полагаем, что оно не
видно.
100. В точке (х; у)
стоит человек ((х; у) не может лежать на ломаной). Считая, ч го каждому звену
ломаной ставится в соответствие пара номеров концевых вершин, указать, какие
звенья человек увидит полностью или частично, а какие — вообще не увидит. Если
при взгляде звено видно как точка или как пара точек, то полагаем, что оно не
видно.
![]() 28. На гранях двух равных правильных
тетраэдров N и М написаны числа Nl, ЛЬ, N3, N4 и М), ЛЬ, мз, М4. Можно ли
совместить тетраэдры так, чтобы на совпадающих гранях оказались одинаковые
числа?
28. На гранях двух равных правильных
тетраэдров N и М написаны числа Nl, ЛЬ, N3, N4 и М), ЛЬ, мз, М4. Можно ли
совместить тетраэдры так, чтобы на совпадающих гранях оказались одинаковые
числа?
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Заданы стороны А и В двух квадратов, расположенных так, как показано на рисунке 25 (вертикальные оси симметрии у квадратов совпадают). Определить угол а, под которым шарик надо выпустить из точки А, чтобы он попал в точку В за минимальное количество отражений.
2. Два
![]() на
плоскости задаются координатами вершин в порядке их обхода по контурам. Найти
минимальное расстояние между этими
на
плоскости задаются координатами вершин в порядке их обхода по контурам. Найти
минимальное расстояние между этими![]()
З. N точек на плоскости заданы своими координатами. Найти
порядок, в котором можно соединить эти точки, чтобы получилась ломаная без
самопересечений. 4. На плоскости задано N точек с координатами ![]() (х; уп).
Найти такую точку Z (х; у), сумма расстояний от которой до остальных минимальна
и:
(х; уп).
Найти такую точку Z (х; у), сумма расстояний от которой до остальных минимальна
и:
а) Z — одна из заданных точек;
б) Z — произвольная точка плоскости.
5. На плоскости задано множество точек А и множество прямых В. Найти две такие различные точки из А, что проходящая через них прямая параллельна наибольшему количеству прямых из В.
6. Среди треугольников с вершинами в заданном множестве точек на плоскости указать такой, стороны которого содержат максимальное число точек заданного
множества.
7.
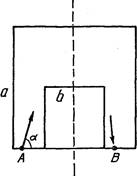 Все стены дома имеют длину 5 м. Северная и южная стороны —
белые, западная и восточная — синие. Человек јтрошел от юго-восточного угла
дома А метров на юг, В метров на восток и С метров на север и посмотрел на дом.
Написать алгоритм, который определяет, какие стены увидит человек.
Все стены дома имеют длину 5 м. Северная и южная стороны —
белые, западная и восточная — синие. Человек јтрошел от юго-восточного угла
дома А метров на юг, В метров на восток и С метров на север и посмотрел на дом.
Написать алгоритм, который определяет, какие стены увидит человек.
8.
На столе лежит игральный кубик гранью Ао к нам, гранью Рис. 25 Во вверх.
Написать программу, определяющую последовательность «кантования» кубика («на
нас», «от нас», «вправо», «влево»), после выполнения которых кубик окажется на
прежнем месте, но к нам гранью Ак, вверх — Вк![]()
П р и м е ч а н и е. Под кантованием понимается перекатывание кубика через соприкасающееся со столом ребро без скольжения. Другие способы перемещения кубика запрещены. Нумерация граней кубика такова, что если его положить на грань с цифрой 5, то боковые грани будут иметь номера 1, 6, 4, З при обходе по часовой стрелке, а верхняя — номер 2.
9. На плоскости заданы координаты вершин двух треугольников. Требуется найти хотя бы одну прямую, разбивающую каждый из этих треугольников на две равновеликие части. Результат должен выводиться на экран в виде уравнения y=kx+b. Если искомая прямая параллельна оси Оу, то уравнение должно быть приведено в виде х=А. Коэффициенты А, В, К должны быть приведены не менее чем с четырьмя знаками после десятичной точки.
10. Даны числа (Xl•, И), (х; И), ( хз; Уз) — координаты трех каких-то вершин прямоугольника в прямоугольной системе координат. Найти координаты четвертой вершины.
11. Будем отсчитывать углы от положительного направления оси Ох: положительные — против часовой стрелки, отрицательные — по часовой стрелке. Пусть величина угла лежит в пределах от —180 0 до 180 0 . Даны 2 точки А (Xf, щ) и В (х; И). Определить, какой из отрезков, ОА или ОВ, образует больший угол с осью Ох.
12. ![]() Задается
число N и точки плоскости щ), (х; И), . . . , хм; YN), являющиеся серединами
последовательных сторон Восстановить по этим точкам исходный Под
многоугольником в данной задаче понимается какая угодно (возможно
самопересекающаяся) замкнутая ломаная.
Задается
число N и точки плоскости щ), (х; И), . . . , хм; YN), являющиеся серединами
последовательных сторон Восстановить по этим точкам исходный Под
многоугольником в данной задаче понимается какая угодно (возможно
самопересекающаяся) замкнутая ломаная.
П р и м е ч а н ие. ![]() и N<20, Xi, уј — вещественные числа. Входные данные
будут соответствовать приведенным условиям, причем многоугольник построить
можно. Структура вывода: точка 1: А [1] В [1] точка 2: А [21 В [2]
и N<20, Xi, уј — вещественные числа. Входные данные
будут соответствовать приведенным условиям, причем многоугольник построить
можно. Структура вывода: точка 1: А [1] В [1] точка 2: А [21 В [2]
точка N•. А [N] В [М, где (А [il; В — координаты вершины контура искомого многоугольника.
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
ПОВЫШЕННОЙ СЛОЖНОСТИ
1. ![]()
![]() Вариант 1.
Можно через концы отрезка провести прямую y=cx+d и определить, принадлежит ли
точка пересечения двух прямых, если она существует, отрезку, т. е. мы должны
решить уравнение х (с— К) —
Вариант 1.
Можно через концы отрезка провести прямую y=cx+d и определить, принадлежит ли
точка пересечения двух прямых, если она существует, отрезку, т. е. мы должны
решить уравнение х (с— К) — ![]() найти и проверить выполнение неравенств Но
при нахождении (х; у) в результате деления могут возникнуть большие
вычислительные погрешности или даже переполнение или потеря значимости, в
результате чего получится неверный ответ.
найти и проверить выполнение неравенств Но
при нахождении (х; у) в результате деления могут возникнуть большие
вычислительные погрешности или даже переполнение или потеря значимости, в
результате чего получится неверный ответ.
Вариант 2. Обозначим Е (х; ![]() Прямая
Прямая
Кх+Ь=у разбивает плоскость на три части: в одной Р (х; в другой F(x; у и на прямой Кх+Ь=у выполняется F (x; Если прямая y=kx+b пересекает отрезок, то либо концы отрезка лежат в различных полуплоскостях, либо хотя бы одна концевая точка отрезка лежит на прямой. Это равносильно выполнению неравенства F(xt•, щ) F (х; Таким образом, не вычисляя точку пересечения, мы по знаку произведения можем определить, имеют ли прямая и отрезок общую точку. Очевидно, что второй вариант решения задачи предпочтительнее первого.
2. Точки отрезка Z можно описать уравнением
![]()
где р число
![]() 1),
ОВ и ОС— векторы.
1),
ОВ и ОС— векторы.![]()
![]() Если существует такое число р
Если существует такое число р ![]() 1),
что
1),
что ![]() то А лежит на отрезке, иначе
то А лежит на отрезке, иначе ![]() нет.
нет.
Равенство расписывается покоординатно так:
![]()
Из первого уравнения находим р, подставляем
во второе; если получаем равенство и ![]() то А лежит на отрезке, иначе нет.
то А лежит на отрезке, иначе нет.
З. Найдем какую-нибудь внутреннюю точку А (х; у) выпуклого многоугольника, например точку А (х; у) с координатами ((Xl +х2+хз)/З; (141 -Ку* уз)/ З). Такая точка называется центром масс треугольника с вершинами в этих трех точках. На контуре выберем произвольно две последовательные вершины Ll и L2 и вычислим углы, которые образуют отрезки (А; Ц) и (А; L2) с осью Ох. Если первый угол меньше второго, то обход против часовой стрелки, иначе — по часовой.
Можно решать задачу и другим способом, который применим и в случае невыпуклой фигуры. Вначале найдем номер вершины, имеющей минимальную у-координату (пусть ее координаты (хо; ут Если таких точек несколько, то берем ту, у которой х-координата минимальна (т. е. самую левую). После этого мы знаем координаты двух точек, одна из которых предшествует в заданном обходе найденной точке, а другая — следует за ней. Пусть ИХ координаты (хр; ур) И (Х; ys) соответственно. Если
Ys--Ymtn
(ХР — + (ур — Ymin)2 (xs —ХО)2 + (ys — Ymin)Q
то обход по часовой стрелке, иначе — против (значения дробей соответствуют косинусам углов, которые образуют соответствующие стороны многоугольника с прямой, определяемой уравнением y=ymin. А так как этот угол лежит в пределах от 00 до l80 0 , то меньшему углу соответствует большее значение косинуса).
4.
Предположим, мы нашли такую прямую. Будем сдвигать ее в направлении,
перпендикулярном этой прямой (параллельный перенос) до тех пор, пока она не
пересечет какую-нибудь из концевых точек отрезка. За счет поворота прямой
вокруг этой точки мы можем добиться того, что прямая будет проходить через 2
концевые точки отрезков и не перестанет быть решением задачи. Следовательно, мы
должны рассмотреть прямые, проходящие через все возможные комбинации пар
концевых точек отрезков. Всего надо проверить (2N— ![]()
![]() + (2N— 1) прямых
и для каждой из них найти число пересечений с отрезками. Та прямая, у которой
это число максимальное, и есть искомая.
+ (2N— 1) прямых
и для каждой из них найти число пересечений с отрезками. Та прямая, у которой
это число максимальное, и есть искомая.
При решении возникает подзадача пересечения прямой ![]() и
отрезка с концами (хв щ), (х; У2). (См. алгоритм 1,3.)
и
отрезка с концами (хв щ), (х; У2). (См. алгоритм 1,3.)
5. Строим выпуклую оболочку данного множества точек, т. е. такой выпуклый многоугольник, вершинами которого являются некоторые из этих N точек (возможно, не все). Через какое бы ребро этого многоугольника мы не провели прямую, все N точек исходного множества будут лежать по одну сторону от этой прямой и на ней (определение местоположения точек относительно прямой — см. алгоритм 1.3).
Из произвольной точки at множества А из N точек мы можем провести не более (N— 1 )-го отрезка так, чтобы и вторая концевая точка этого отрезка была из множества А. Берем тот отрезок [щ; ф], для которого все точки множества А лежат по одну сторону от прямой, проходящей через этот отрезок (если ни один отрезок не удовлетворяет этому условию, то берем другое а1•, с самого начала лучше всего взять в качестве at точку с максимальной абсциссой, а если таких несколько, то среди них берем точку с максимальной ординатой — это гарантирует, что al принадлежит искомому контуру выпуклого многоугольника). Для точки а2 ищем точку аз * а; так, чтобы все множество А лежало по одну сторону от прямой, определяемой отрезком [а; аз], ДЛЯ ТОЧКИ ај ищем точку ai+l +ai_l так, чтобы все точки А лежали по одну сторону от прямой, содержащей отрезок [щ, щ +1], и т. д., до тех пор, пока очередной точкой ai+l не станет 01, — мы замкнули контур и нашли выпуклую оболочку.
Все точки множества А, не лежащие на контуре, лежат внутри выпуклой оболочки.
6.
![]() Предположим, что мы построили искомый выпуклый многоугольник. Если
какая-то точка а (из данного
Предположим, что мы построили искомый выпуклый многоугольник. Если
какая-то точка а (из данного ![]() в условии множества S из К точек) лежит на
стороне многоугольника, то считаем ее новой вершиной этого многоугольника.
Можем считать, что все вершины данного многоугольника есть точки множества S
(если это не так и между двумя точками а и Ь из S лежит одна или несколько
«посторонних» вершин, то мы можем их отбросить и считать, что а и Ь — две
последовательные вершины контура. Многоугольник при этом у нас остается
выпуклым (отрезок [а; Ь] делит фигуру на два выпуклых многоугольника), а так
как на контуре между а и Ь не лежало ни одной точки из S, то полученный
многоуголь
в условии множества S из К точек) лежит на
стороне многоугольника, то считаем ее новой вершиной этого многоугольника.
Можем считать, что все вершины данного многоугольника есть точки множества S
(если это не так и между двумя точками а и Ь из S лежит одна или несколько
«посторонних» вершин, то мы можем их отбросить и считать, что а и Ь — две
последовательные вершины контура. Многоугольник при этом у нас остается
выпуклым (отрезок [а; Ь] делит фигуру на два выпуклых многоугольника), а так
как на контуре между а и Ь не лежало ни одной точки из S, то полученный
многоуголь![]() ник удовлетворяет требованиям задачи).
ник удовлетворяет требованиям задачи).
Итак, в качестве решения задачи мы получили выпуклую оболочку множества S (о построении ее см. задачу 5).
Если построенная выпуклая оболочка такова, что каждая точка S является ее вершиной (или лежит на стороне), то задача решена, иначе — решения не существует.
7. Рассмотрим два из возможных алгоритмов.
Вариант 1. Строим выпуклую оболочку данного множества точек (см. задачу 5).
Если все точки множества А лежат на контуре, то ![]() задача
решена. Если же нет, то ищем точку р с минимальным расстоянием до контура (если
таких точек несколько, то берем любую из них). Пусть минимальное расстояние до
контура есть расстояние до стороны (и; о).
задача
решена. Если же нет, то ищем точку р с минимальным расстоянием до контура (если
таких точек несколько, то берем любую из них). Пусть минимальное расстояние до
контура есть расстояние до стороны (и; о).
43
Вставляем в контур точку р: вместо контура . ![]() будет
контур
будет
контур![]()
Для оставшихся точек повторяем описанную выше процедуру, пока все точки не будут вставлены в контур.
Расстояние от точки до стороны — это либо длина
перпендикуляра, опущенного из точки на сторону, если проекция точки попадает на
отрезок, либо минимальное из расстояний от точки до концевых точек стороны.
Расстояние от точки 2 (и; о) до ее проекции на прямую ![]() ест Ь А 2 +В
2 .
ест Ь А 2 +В
2 .
Вариант 2. Строим выпуклую оболочку V данного множества точек.
Если все точки множества А лежат на контуре, то задача
решена. Иначе, обозначим через А 1 все внутренние точки выпуклой оболочки У.
Строим для нового множества 141 выпуклую оболочку V1 (контуры V и Vl не
пересекаются !![]()
«Склеиваем» два контура следующим образом.
Выберем по паре последовательных вершин р, s и Т, Sl на контурах V и соответственно так, чтобы в четырехугольнике с вершинами s, р, Р), не лежало больше никаких других точек контуров V и И. Разрываем контуры V и Vl (убирая ребра (р; s ) и (щ; Sl)) и объединяем их (добавляя ребра (р; р) и (s; Sl)).
Если внутри нет внутренних точек, то задача решена, иначе — с внутренними точками Vl проделываем те же самые операции: находим выпуклую оболочку и пары последовательных точек на контура& разрываем и «склеиваем» контуры и т. д., пока не получим, что последняя построенная выпуклая оболочка содержит в себе 0, 1 или 2 точки.
Если точек О, то задача решена. В
противном случае присоединяем точки к ранее образованному контуру так, ![]() чтобы
фигура осталась многоугольником (можно проводить присоединение, как и в
варианте l).
чтобы
фигура осталась многоугольником (можно проводить присоединение, как и в
варианте l).
![]() 8. У клеточной фигуры могут быть
следующие оси симметрии — горизонтальная, вертикальная и идущие под углом 450
и l35 0 (т. е. 4 оси симметрии, как у квадрата). Оси могут
проходить как через центр какой-то клетки, так и по стороне. Например, фигуры
8. У клеточной фигуры могут быть
следующие оси симметрии — горизонтальная, вертикальная и идущие под углом 450
и l35 0 (т. е. 4 оси симметрии, как у квадрата). Оси могут
проходить как через центр какой-то клетки, так и по стороне. Например, фигуры
и
имеют по 2 оси симметрии горизонтальную и вертикальную, а фигура * — все 4 оси симметрии.
Введем систему координат таким образом, что каждая зарисованная клетка представляется точкой с целочисленными координатами.
Находим возможный центр симметрии фигуры, имеюЩИЙ координаты
((xmax-l- xmin)/2; (утах -Fymin)/2), где Хгваю ![]() таю xmin и ymin
соответственно максимальные И МИНИмальные иксовые и игрековые координаты точек
в заданной нами системе координат:
таю xmin и ymin
соответственно максимальные И МИНИмальные иксовые и игрековые координаты точек
в заданной нами системе координат:
хтах — тах {хј, Утах —— тах {уД, хmin min min {уј.
Если у фигуры есть ось симметрии, то она проходит через возможный центр симметрии фигуры.
![]() Рассматриваем 4 возможные оси симметрии,
проходящие через этот центр. Определяем, является ли фигура симметричной
относительно каждой из осей (для удобства этот центр можно считать началом
системы координат). При симметрии относительно горизонтальной (вертикальной)
оси каждой клетке фигуры (х; у) должна соответствовать клетка с такой же
иксовой (игрековой) координатой, но с обратной по знаку другой координатой, т.
е. (х; — у) (для вертикальной оси соответственно (— х; у)). При симметрии
относительно оси с наклоном 45 0 (—45 0 ) каждой клетке
(х; у) фигуры должна соответствовать клетка с координатой (у; х) (соответственно
( — у; х)).
Рассматриваем 4 возможные оси симметрии,
проходящие через этот центр. Определяем, является ли фигура симметричной
относительно каждой из осей (для удобства этот центр можно считать началом
системы координат). При симметрии относительно горизонтальной (вертикальной)
оси каждой клетке фигуры (х; у) должна соответствовать клетка с такой же
иксовой (игрековой) координатой, но с обратной по знаку другой координатой, т.
е. (х; — у) (для вертикальной оси соответственно (— х; у)). При симметрии
относительно оси с наклоном 45 0 (—45 0 ) каждой клетке
(х; у) фигуры должна соответствовать клетка с координатой (у; х) (соответственно
( — у; х)).
 9. Отрезки, соединяющие точки разбиений R 1 и Ю,
параллельны стороне AD. Будем брать отрезки, соединяющие последовательные точки
разбиений R3 и R4, и искать между этими двумя последовательными отрезками
четырехугольник с наибольшей площадью. Четырехугольник разбиения Q с
максимальной площадью есть четырехугольник с максимальной площадью по всем
таким разбиениям прямоугольника отрезками.
9. Отрезки, соединяющие точки разбиений R 1 и Ю,
параллельны стороне AD. Будем брать отрезки, соединяющие последовательные точки
разбиений R3 и R4, и искать между этими двумя последовательными отрезками
четырехугольник с наибольшей площадью. Четырехугольник разбиения Q с
максимальной площадью есть четырехугольник с максимальной площадью по всем
таким разбиениям прямоугольника отрезками.
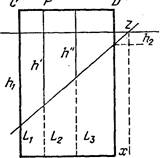
Пусть последовательные точки разбиения с одинаковыми номерами на сторонах
ВС и AD есть соответственРис. 26 но ;2 и Д2•
Если ![]() анализируемые
четырехугольники есть прямоугольники, и прямоугольник с максимальной площадью
определяется максимальной длиной отрезка в разбиении R 1 (или, что то же, R2).
анализируемые
четырехугольники есть прямоугольники, и прямоугольник с максимальной площадью
определяется максимальной длиной отрезка в разбиении R 1 (или, что то же, R2).
Пусть для определенности 72—fl ![]() (случай обратного
неравенства рассматривается аналогично). Обозначим il =Т,
(случай обратного
неравенства рассматривается аналогично). Обозначим il =Т, ![]() P=CD, и h”
P=CD, и h” ![]() длины
левой и правой сторон четырехугольника, L2 — расстояние между двумя этими
сторонами, Z — точка пересечения продолжения верхней и нижней сторон
четырехугольника: Ц, L3 — соответственно расстояния от левой и правой стенок
прямоугольника ABCD до четырехугольника, х — расстояние от точки Z до
прямоугольника ABCD, S — площадь четырехугольника. Получим следующую схему
(рис. 26) и равенства:
длины
левой и правой сторон четырехугольника, L2 — расстояние между двумя этими
сторонами, Z — точка пересечения продолжения верхней и нижней сторон
четырехугольника: Ц, L3 — соответственно расстояния от левой и правой стенок
прямоугольника ABCD до четырехугольника, х — расстояние от точки Z до
прямоугольника ABCD, S — площадь четырехугольника. Получим следующую схему
(рис. 26) и равенства:
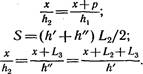
Откуда х = ph2/(hl — Ь);
![]() = h2 (х + 1-.,2 + L3)/x;
= h2 (х + 1-.,2 + L3)/x; ![]() = h2 (Х + L3)/X.
= h2 (Х + L3)/X.
![]() KaXAOÜ napb} OTPe3KOB, onpeme.nneMblx TOMKaMH pa36meHHü R3 H R
4, Hax0ÅHM MaKCHMaJ1bHYEO fl.nouaAb qeTb1pexY1'0J1bHHKa Mencmy 9THMH
OTPe3KaMH.
KaXAOÜ napb} OTPe3KOB, onpeme.nneMblx TOMKaMH pa36meHHü R3 H R
4, Hax0ÅHM MaKCHMaJ1bHYEO fl.nouaAb qeTb1pexY1'0J1bHHKa Mencmy 9THMH
OTPe3KaMH.
10. nycTb KOOPAHHaTb1 Toqex Xl, He y6blBaK)T (ec,nq 3T0 He TaK, TO npocT0 0TcopTupyeM mpeABapvrreJ1bH0 110CJ1eAOBaTeJ1bHOCTb).
BapuaHT l. FIpeA110JIO>KHM, MTO Mbl HaLUJIH TOMKY Z C KOOPAHHaTOÜ XO H OHa JIOKHT Ha HHTepBaene (X • X ). CnpaBa 0T Hee i ToqeK, cneBa — (N —i). CYMMa paCCTORHHÜ Smn 6ymeT Taxoh:
![]() —XO) + + (xN — XO).
—XO) + + (xN — XO).
IIpeÄTIOJIO>KHM, r-1T0
i > N —i H Mbl B npeme.nax MHTepBaJia CABqraeM TO LIKY Z BJ1eBO
Ha KaKYK)-TO Ma,neHbKYÆO BeJIMMHHY d ![]() F10J1yqaeM HOBYK) cyMMY S:
F10J1yqaeM HOBYK) cyMMY S:
![]()
A TaK KaK no rrpeA110J10hßHHK) i > N —i, TO S < Smin •
CHTyaLUåfl, K0FÅa N—i>i, ncc.nemyeTcH aHa,norH 11H0 —
me,naeM CABHP Ha BeJJh LIHHY d < xN+l—XO mpaB0, He BblXO![]() 9TOM 3a rpaHHLLb1 HHTepBajra, H onflTb
me no,nyqaeM, t4T0 HOBafl CYMMa S < Smin. CJ1yqaü, KORAa Z
coBnamaeT C OAHO#i H3 ToqeK Xi, HCCJ1emyeTcq eraK Me, C
HCflOJ1b30BaHHeM Ma,neHbKMX CABHROB.
9TOM 3a rpaHHLLb1 HHTepBajra, H onflTb
me no,nyqaeM, t4T0 HOBafl CYMMa S < Smin. CJ1yqaü, KORAa Z
coBnamaeT C OAHO#i H3 ToqeK Xi, HCCJ1emyeTcq eraK Me, C
HCflOJ1b30BaHHeM Ma,neHbKMX CABHROB.
C,neAOBaTeJ1bHO, Toro I-ITC6b1 ToqKa Z 6b1,na HCKOMOü, He06XOAUMO H AOCTaT04HO, qT06b1 cnpaBa H CJ1eBa 0T Hee JlexaJIO OJIHO H TO xe MHCJIO 'roqeK. ECJIH N = 2k, TO T0MKa Z MO>KeT 6b1Tb Jl}060i H3 'roqeK 0TpeaKa [Xk', Xk+l], ecJIM me N=2k+1, TO TOMKa Z HMeeT KOOPÅHHaTY Xk+l. BapuaHT 2. NYCTb Mb! pemaeM 3aÅayy N 'rogeK Ha apHM0ü.
ToqKa Z AOJ1>KHa, oqeBHAHO,
.ne>KaTb Ha 0Tpe3Ke [Xf, XN]. ECJIH N = l, TO maHHaH ToqKa H ABJ1qeTCf1 HCKOMOVI. ECJTH N =
2, TO Z MO>KeT JlexaTb rue yr0AH0 Ha otpe3Ke ![]() cyMMapHoe pacCT0flHHe 6ymeT OAHHaKOBb1M
H pagHb1M AJIHHe ompe3Ka.
cyMMapHoe pacCT0flHHe 6ymeT OAHHaKOBb1M
H pagHb1M AJIHHe ompe3Ka.![]()
Если N>2, то суммарное расстояние от точки Z до точек с минимальной и максимальной координатами (т. е. до точек и XN) не зависит от местоположения точки Z и равно длине отрезка [хь XN].
Так как суммарное расстояние до этих двух точек постоянно, то поэтому мы их можем не рассматривать и решать далее задачу уже для (N—2) точек х2, ..., XN_l. Проведя необходимое число раз сокращение количества точек, мы придем к уже рассмотренным случаям одной или двух точек.
Окончательно получаем: если N=2k, то точка Z может быть любой
из точек отрезка [хк; хк +1], если же N— ![]() 1, то точка Z имеет
координату хк +1.
1, то точка Z имеет
координату хк +1.
11. Переформулируем задачу: На плоскости своими координатами задаются N точек Р, (х; у). Построить окружность минимального радиуса с центром на оси абсцисс так, чтобы она содержала внутри себя и на своей границе все эти точки.
![]() Везде в дальнейшем будем обозначать через
С (Р; Z) окружность с центром в точке (Р; О) и проходящую через точку Z (х; у).
Везде в дальнейшем будем обозначать через
С (Р; Z) окружность с центром в точке (Р; О) и проходящую через точку Z (х; у).
Очевидно, что на искомой окружности лежит, по меньшей мере, одна точка. Действительно, в противном случае мы можем, не меняя центра окружности, уменьшить ее радиус, а это противоречит предположению о том, что нами была построена окружность минимального радиуса.
Докажем следующее простое утверждение: если на искомой окружности лежит единственная +ьчка, то центр окружности есть проекция этой точки на ось абсцисс.
Предположим противное — на минимальной окружности лежит
единственная точка Z(x у), а центр ее не совпадает с (х; 0). Если мы начнем
понемножку двигать центр окружности, проходящей через точку Z, в направлении
(х; 0), то, так как все точки, кроме Z, лежат внутри окружности, до какого-то
момента они и будут оставаться внутри нее. Таким образом мы можем хоть
чуть-чуть, ![]() но сдвинуть центр, уменьшив при этом
радиус окружности, содержащей все точки. Получаем противоречие
но сдвинуть центр, уменьшив при этом
радиус окружности, содержащей все точки. Получаем противоречие ![]() с
предположением о минимальности радиуса.
с
предположением о минимальности радиуса.
Следствие. Если на искомой окружности лежит только одна точка, то это точка с максимальной по модулю ординатой.
Отметим, что окружность с центром на оси абсцисс ![]() единственным
образом определяется двумя лежащими на ней точками (центр этой окружности — это
точка пересечения оси абсцисс и серединного перпендикуляра к отрезку,
соединяющего эти две точки).
единственным
образом определяется двумя лежащими на ней точками (центр этой окружности — это
точка пересечения оси абсцисс и серединного перпендикуляра к отрезку,
соединяющего эти две точки).
![]() Вариант 1.
Вариант 1.
Шаг 1. Ищем точку (х; И) с максимальной по модулю ординатой (если таких точек несколько и у них разные абсциссы, то перейти на Шаг 2) и для окружности С (х; (х; yD) проверяем, содержит ли она все N точек. Если да, то задача решена, если нет, то переходим к шагу 2.
Шаг 2. Среди окружностей, определяемых всевозможными парами точек (Р; Рј), находим те, которые содержат все точки, а затем выбираем из них окружность минимального радиуса.
Пар точек, которые могут определять окружности, всего N (N— 1)/2, т. е. порядка N2, следовательно, и возможных окружностей тоже порядка N2. Для проверки принадлежности N точек каждой окружности требуется порядка N операций. Получаем, что сложность этого алгоритма порядка N3. (Когда мы говорим о сложности алгоритма, то рассматриваем только зависимость роста числа требуемых операций от числа N, игнорируя все константные множители и медленно растущие слагаемые.) Рассмотрим другой способ решения этой задачи, основанный на более глубоком ее анализе.
![]() Вариант 2.
Вариант 2.
Проверка по Шагу ранее изложенного алгоритма остается без изменения. Пусть искомая окружность не найдена. Для обоснования Шага 2 докажем следующее утверждение:
Пусть окружность с центром (Pii, О) определяется точками Pi(Xf, уј) и Рј(хј; уј). Она только тогда может быть содержащей все точки окружностью С минимального радиуса, когда (Ри; 0) лежит на ортогоналъной проекции отрезка [(Xf, И); (х; уј)] на ось абсцисс, т. е. должны выполняться неравенства xkPij<x..
![]() Окружность С с центром (Ри; О) должна
проходить не менее чем через две точки заданного множества из N точек, и при
этом из исходных точек всегда можно выбрать две такие (обозначим ИХ Pi (Х; Yi)
И Рј (хј; уј)), что
Окружность С с центром (Ри; О) должна
проходить не менее чем через две точки заданного множества из N точек, и при
этом из исходных точек всегда можно выбрать две такие (обозначим ИХ Pi (Х; Yi)
И Рј (хј; уј)), что ![]() Действительно, если бы абсциссь1 всех лежащих
на окружности точек были, например, меньше РЕЈ, то (Ри; 0) можно было бы
сместить влево по оси абсцисс на некоторую величину с уменьшением радиуса
охватывающей все точки окружности, что противоречит минимальности найденной
ранее окружности.
Действительно, если бы абсциссь1 всех лежащих
на окружности точек были, например, меньше РЕЈ, то (Ри; 0) можно было бы
сместить влево по оси абсцисс на некоторую величину с уменьшением радиуса
охватывающей все точки окружности, что противоречит минимальности найденной
ранее окружности.
Ни одна из точек, лежащих на окружности, не может иметь абсциссы Pii вследствие невыполнения условия Шага 1.
Итак: всегда можно найти две лежащие на окружности точки РЕ и Рј с абсциссами соответственно меньше и больше абсциссы центра окружности. Эти точки определяют центр окружности (Ри; О) — точку пересечения серединного перпендикуляра К отрезку [Рј; Рј] С ОСЬЮ абсцисс. При этом точка (Рт; 0), естественно, будет лежать на проекции отрезка [Рг, Рј] на ось абсцисс.
Рассматривая все пары точек (Р; Рј), таких, что точка
пересечения (Ри; 0) серединного перпендикуляра к отрезку [Р; РА с осью абсцисс
лежит на“ проекции отрезка [Р; Рј] на ось абсцисс, получаем, что центр ![]() искомой
окружности минимального радиуса совпадает с одной из таким образом полученных
точек. Каждая из рассматриваемых пар точек (Р; Рј) определяет окружность
минимального радиуса Rii, содержащую эти две точки.
искомой
окружности минимального радиуса совпадает с одной из таким образом полученных
точек. Каждая из рассматриваемых пар точек (Р; Рј) определяет окружность
минимального радиуса Rii, содержащую эти две точки.
Из всего вышесказанного получаем, что интересующая нас окружность минимального радиуса, содержащая М точек, должна иметь максимальный из всех полученных радиусов RiI.
![]() Всего пар точек (РБ PI) не более (N2 —
N)/2, и, следовательно, сложность алгоритма:
Всего пар точек (РБ PI) не более (N2 —
N)/2, и, следовательно, сложность алгоритма:
![]()
Здесь мы, как и обычно, избавляемся от констант и медленно растущих слагаемых.
![]() Вариант З.
Вариант З.
Все вычисления на машине проводятся с ограниченной точностью, с определенным числом знаков после запятой. Поэтому нам бывает достаточно только указать, что интересующая нас точка лежит внутри отрезка заранее заданной длины epsilon. Epsilon задается пользователем. Например, если мы хотим найти координату точки с точностью 5 знаков после запятой, то epsilon=
—6
В отличие от варианта 2 мы не будем брать все перпендикуляры, попадающие на проекции отрезков, и искать среди получаемых окружностей окружность с максимальным радиусом. Наоборот, описанным ниже способом будем выбирать точку на оси абсцисс и проверять, является ли она искомой или нет.
Из варианта решения 2 можно сделать вывод, что искомая точка
лежит на отрезке [АО, ![]() {хД, тах {Xi}]. Пусть Во)/2 — середина
этого отрезка, а — его длина.
{хД, тах {Xi}]. Пусть Во)/2 — середина
этого отрезка, а — его длина.
Обозначим:
Dl (Со) — максимальное из расстояний от точки (Со; 0) до точек (х; И) с абсциссами х •
Dr (Со) — максимальное из расстояний от точки (Со; 0) до точек (х; И) с абсциссами Со.
Опишем Ј-й итеративный (повторяющийся) шаг алгоритма (i=O, I ![]() ЕСЛИ
ЕСЛИ![]()
ТО центр окружности лежит на отрезке [А; Ц] и желаемая точность достигнута. Стоп.
ИНАЧЕ
Вычисляем ![]() Bi)/2
Bi)/2
Находим Dl (Ci) и Dr (Ci)
ЕСЛИ![]()
ТО искомая точка не может лежать на промежутке [Д; СЛ, так как радиус любой содержащей N точек окружности с центром на этом промежутке больше Dr (Ci) (проверьте сами!), а окружность с центром Ci имеет радиус Dr (С). Поэтому центр искомой окружности лежит на отрезке [С; Д], который мы обозначим
![]()
ИНАЧЕ
ЕСЛИ![]()
ТО получаем, что центр искомой
окружности лежит на [АБ СЕ], который мы обозначим [Д + й, Bi+l] ![]() ИНАЧЕ
ИНАЧЕ
ЕСЛИ![]()
ТО Ci — центр искомой окружности. Стоп ![]() Конец
Ј-го итеративного шага. Выполнить шаг Н- 1
Конец
Ј-го итеративного шага. Выполнить шаг Н- 1
Мы видим, что длина L начального отрезка на каждом шаге уменьшается вдвое. Алгоритм, вообще говоря, заканчивает работу при выполнении условия L/(2S ) epsilon.
При меча н и е. Таким образом, требуется не более чем S
= ![]() шагов, где log2 — это логарифм по основанию 2. Так как на каждом шаге
(для вычисления Dl и Dr) выполняется не более 0 (N) операций, то всего их
потребуется порядка О (N 10Д2 (L/epsilon)).
шагов, где log2 — это логарифм по основанию 2. Так как на каждом шаге
(для вычисления Dl и Dr) выполняется не более 0 (N) операций, то всего их
потребуется порядка О (N 10Д2 (L/epsilon)).
12. Это переборная задача. Обратите внимание, что стороны квадрата могут и не быть параллельны осям координат! Каждую из N точек мы последовательно рассматриваем в качестве верхнего левого угла квадрата, каждую из оставшихся М— 1 — как нижнюю правую вершину и смотрим, есть ли для них в этом множестве из N точек точки, соответствующие верхнему правому и нижнему левому углам. Если да, то подсчитываем, сколько точек лежит в данном квадрате.
Пусть координата левого верхнего угла (хь щ), нижнего правого — (х; И), тогда координата пересечения диагоналей квадрата:
(( X l + х2)/ 2 ; (Yl +Y2)/2 ); координата верхнего правого угла:
![]() + х2)/2 + [И — (щ -4- У2)/2];
+ х2)/2 + [И — (щ -4- У2)/2];
(Yl + У2)/ 2 -F[X i
— ( X l + ![]() (( Х \ Yl — У2)/ 2 ;
( Х 1 —X2+Yl + У2)/ 2 )'
(( Х \ Yl — У2)/ 2 ;
( Х 1 —X2+Yl + У2)/ 2 )' ![]() нижнего левого:
нижнего левого:
(( X l -F X2—Y1 +У2)/2 ; ( —X l -F X2+Yl![]()
Для ( Ь; щ) и (х; И) должны выполняться следующие неравенства: <х2, (иначе это будут уже не левый верхний и правый нижний углы квадрата).
13. Из координат вершин прямоугольников формируем массивы: массив Xkor, содержащий х-координаты вершин прямоугольников, связанный с ним массив Хпот ' содержащий соответствующие номера прямоугольников, аналогично формируются массивы Уко, и Упот для у-координат. При этом координате вершины ставится в соответствие номер со знаком если вершина левая нижняя, и знак «—», если правая верхняя.
Затем массивы координат сортируют в порядке неубывания (при
этом соответствие между координатами и номерами прямоугольников сохраняется),
причем для одинаковых координат вначале должны располагаться номера левых
(нижних) вершин (т. е. со знаком ![]() а затем номера правых (верхних).
а затем номера правых (верхних).
Задача решается в два этапа. На первом этапе решается задача нахождения максимального числа взаимно пересекающихся отрезков на оси Ох (в качестве отрезков берутся проекции прямоугольников на ось Ох).
![]() Максимальное число взаимно пересекающихся
отрезков находится следующим образом: просматриваем массив Xkor от начала к
концу и увеличиваем на переменную, соответствующую текущему числу пересечений,
если просматриваемая координата соответствует левому концу отрезка, и уменьшаем
эту переменную на 1, если текущая координата соответствует правому концу
отрезка.
Максимальное число взаимно пересекающихся
отрезков находится следующим образом: просматриваем массив Xkor от начала к
концу и увеличиваем на переменную, соответствующую текущему числу пересечений,
если просматриваемая координата соответствует левому концу отрезка, и уменьшаем
эту переменную на 1, если текущая координата соответствует правому концу
отрезка.
Максимальное число взаимно пересекающихся отрезков есть максимальное значение текущего числа пересечений. Заметим, однако, что если для двух прямоугольников их проекции на оси Ох и Оу пересекаются, то прямоугольники пересекаются.
На втором этапе ищется пересечение прямоугольников. Возьмем
некоторую прямую вида у = С (параллельную оси Ох) и все прямоугольники, которые
она пересекает, будем называть активными. Эти прямоугольники в массиве ACT/V
пометим 1, остальные — О.![]()
Теперь, используя результаты первого этапа, с учетов массива ACT/V находится максимальное число взаимно пересекающихся прямоугольников, которые являются активными для рассматриваемого значения С (ищется максимальное число пересекающихся активных прямоугольников).
Теперь определим возможные значения С. Можно ограничиться только теми значениями у, которые соответствуют концевым точкам проекций прямоугольников на ось Оу. Следовательно, формирование массива ACT/V может осуществляться по следующему принципу: отсортировав у-кобрдинаты проекций по неубыванию значений (с учетом того факта, что для нескольких одинаковых координат вначале располагаютсд координаты, соответствующие верхним концам отрезков, а затем располагаются координаты, соответствующие нижним концам отрезков).
Просматривая массив от начала к концу, мы активизируем прямоугольник, если текущая координата соответствует нижнему концу проекции, или отменяем активность прямоугольника, если текущая координата соответствует верхнему концу проекции. Процесс формирования массива ACT/V начинаем при значении переменной С, равной минимальной у-координате (вначале все элементы массива равны 0). Алгоритм заканчивает работу при значении переменной С, равной максимальной у-координате.
14. Понятно, что если есть свеча с нулевыми координатами или какие-нибудь две свечи лежат на прямой, проходящей через начало координат, по разные стороны от начала координат, то решения не существует.
![]() Пусть таких свеч нет. Проведем линию через центр и первую
свечу (пусть это точка А). Если все свечи оказались по одну сторону от прямой,
то решение построено. Предположим, что существуют свечи по разные стороны
прямой. Определим направление прямой от центра к свече, и пусть М — множество
точек, лежащих по правую сторону от прямой. Определим среди них точку В, для
которой угол АОВ максимальный и лежит в пределах от 0 0 до 180 0
. Проведя прямую через точки О и В, проверяем, лежат ли все свечи по одну
сторону от нее. Если да, то решение найдено. Если нет, то решения нет.
Пусть таких свеч нет. Проведем линию через центр и первую
свечу (пусть это точка А). Если все свечи оказались по одну сторону от прямой,
то решение построено. Предположим, что существуют свечи по разные стороны
прямой. Определим направление прямой от центра к свече, и пусть М — множество
точек, лежащих по правую сторону от прямой. Определим среди них точку В, для
которой угол АОВ максимальный и лежит в пределах от 0 0 до 180 0
. Проведя прямую через точки О и В, проверяем, лежат ли все свечи по одну
сторону от нее. Если да, то решение найдено. Если нет, то решения нет.
15. Припишем сторонам каждого из N прямоугольников ориентацию: левая сторона считается идущей сверху вниз (ориентацию обозначим 1), нижняя — слева направо (2), правая снизу вверх (З), верхняя — справа налево (4). Найдем точки пересечения всех N прямоугольников. Обозначим это множество точек S. Добавим в S угловые точки всех прямоугольников. Каждой из точек S припишем пару, состоящую из двух ориентаций, соответствующих ориентации тех ребер, пересечением которых точка является.
Найдем в множестве S точку с максимальной ординатой. Если
таких точек несколько, то возьмем среди них точку Ро с минимальной абсциссой.
Эта точка лежит на верхней части контура объединения прямоугольников и является
левым верхним углом какого-то прямоугольника. Печатаем Ро. Будем двигаться от
Ро вниз по ребру, пока не встретим одну из точек S (это будет либо точка —
вершина прямоугольника, либо точка пересече![]() ние сторон). Обозначим
эту точку Њ. Ей приписана пара ориентаций (ОК, 02), одна из ориентаций (пусть,
напри
ние сторон). Обозначим
эту точку Њ. Ей приписана пара ориентаций (ОК, 02), одна из ориентаций (пусть,
напри![]() мер, 01) есть 1 (это то ребро, по которому
мы пришли в Р 1). Печатаем Р 1 — очередную вершину контура, и двигаемся из
точки Р) (по ребру какого-то прямоугольника) в направлении 02, пока не
достигнем еще какой-нибудь вершины из S. Обозначим ее У нее пара ориентаций
мер, 01) есть 1 (это то ребро, по которому
мы пришли в Р 1). Печатаем Р 1 — очередную вершину контура, и двигаемся из
точки Р) (по ребру какого-то прямоугольника) в направлении 02, пока не
достигнем еще какой-нибудь вершины из S. Обозначим ее У нее пара ориентаций ![]() (0f;
Об). Пусть, например, 02, тогда мы из очередной вершины контура Р2 будем
двигаться в направлении О]' и т. д., пока не достигнем вершины РО. Контур
выписан.
(0f;
Об). Пусть, например, 02, тогда мы из очередной вершины контура Р2 будем
двигаться в направлении О]' и т. д., пока не достигнем вершины РО. Контур
выписан.
Определим, есть ли в контуре «дырки». Занесем в массив А
[1..2, l..2N] в строку все ординаты вершин прямоугольников без повторений и
отсортируем этот массив по первой строке по возрастанию. Предположим, что в
массиве А хранится всего S различных ординат: ![]() А [1, s]. Сначала вс.е
А [2,
А [1, s]. Сначала вс.е
А [2, ![]() s. Определим массив В [l ..4, l.«N]. В
первой строке массива В располагаются в порядке неубывания х-координаты левых
нижних и правых верхних вершин всех N прямоугольников. Пусть В [1, Ј] —
х-координата какойто вершины Р; В [2, i] и В [З, i] — соответственно ординаты
нижней и верхней вершин той вертикальной стороны прямоугольника, на которой
лежит Р; В [4, если эта вертикальная сторона прямоугольника левая, и 1, если —
правая.
s. Определим массив В [l ..4, l.«N]. В
первой строке массива В располагаются в порядке неубывания х-координаты левых
нижних и правых верхних вершин всех N прямоугольников. Пусть В [1, Ј] —
х-координата какойто вершины Р; В [2, i] и В [З, i] — соответственно ординаты
нижней и верхней вершин той вертикальной стороны прямоугольника, на которой
лежит Р; В [4, если эта вертикальная сторона прямоугольника левая, и 1, если —
правая.
Воспользуемся методом сканирующей прямой. Будем брать
по возрастанию индекса i элементы В [Д, i] масси- ![]() ва В.
ва В.
Если В [4, то будем увеличивать на 1, а если ![]() 1,
то уменьшать на 1 все элементы А [2, ј] такие, что В [2, [1, [З, Ј] (А [2, ј]
будет равно количе-
1,
то уменьшать на 1 все элементы А [2, ј] такие, что В [2, [1, [З, Ј] (А [2, ј]
будет равно количе- ![]() ству прямоугольников, содержащих внутри
себя или на границе отрезок А [1, [2, ј], х = В [1, i]).
ству прямоугольников, содержащих внутри
себя или на границе отрезок А [1, [2, ј], х = В [1, i]).![]()
![]() Если какое-то А [2, то это означает, что прямоугольники
при х— В [1, i] не покрывают интервал у =
Если какое-то А [2, то это означает, что прямоугольники
при х— В [1, i] не покрывают интервал у =
![]()
![]() Если мы найдем такие
Ј, ј и К, что при х— В [1, Ј] интервал (А [1, ј]; А [1, КА- 1]) не покрыт
многоугольника—А [2, а интервалы (А [1, ј покрыты (т. е. А [2, ј— и А [2, и
точка
Если мы найдем такие
Ј, ј и К, что при х— В [1, Ј] интервал (А [1, ј]; А [1, КА- 1]) не покрыт
многоугольника—А [2, а интервалы (А [1, ј покрыты (т. е. А [2, ј— и А [2, и
точка ![]() (х; у)—(В [1, Ј]; А [1, ј]) не принадлежит
внешнему контуру фигуры — объединению прямоугольников, то у фигуры есть по
крайней мере одна «дырка». Чтобы, при необходимости, выписать контур «дырки»,
поступим, как и в случае нахождения внешнего контура,— пойдем по ребрам,
образующим контур «дырки», но обход контура
(х; у)—(В [1, Ј]; А [1, ј]) не принадлежит
внешнему контуру фигуры — объединению прямоугольников, то у фигуры есть по
крайней мере одна «дырка». Чтобы, при необходимости, выписать контур «дырки»,
поступим, как и в случае нахождения внешнего контура,— пойдем по ребрам,
образующим контур «дырки», но обход контура ![]() необходимо будет осуществлять
по часовой стрелке, т. е. против ориентации сторон.
необходимо будет осуществлять
по часовой стрелке, т. е. против ориентации сторон.
Будем выписывать контур точка за точкой, начиная с самой левой точки контура.
Если две соседние горизонтальные площадки имеют одинаковую высоту, то мы их «склеиваем», т. е. рассматриваем как одну площадку.
Если же две соседние площадки различаются по высоте, то, следовательно, надо выписать вертикальный излом контура.
![]() 17. Считаем, что точки в S не дублируются
(так как S — множество). Введем в множество S точки (О; ш), (0; О), (о; 0), (v;
ш)— вершины А. Будем использовать два двумерных массива — ВХ и В У; в массиве
ВХ располагаются координаты точек множества S в порядке неубывания абсциссы, в
ВУ — по невозрастанию ординаты. пара (BX[i, Ц; ВХ [Ј, 2]) (аналогично (ВУ[Ј,
17. Считаем, что точки в S не дублируются
(так как S — множество). Введем в множество S точки (О; ш), (0; О), (о; 0), (v;
ш)— вершины А. Будем использовать два двумерных массива — ВХ и В У; в массиве
ВХ располагаются координаты точек множества S в порядке неубывания абсциссы, в
ВУ — по невозрастанию ординаты. пара (BX[i, Ц; ВХ [Ј, 2]) (аналогично (ВУ[Ј, ![]() ВУ
[ј, 2])) есть х- и у-координаты точки из S.
ВУ
[ј, 2])) есть х- и у-координаты точки из S.
Рассмотрим множество прямоугольников Рј, удовлетворяющих условию задачи. Тот из них, который имеет максимальную площадь, и является искомым. Очевидно, что на каждой из сторон должна лежать точка из S либо сторона Pi должна лежать на стороне А.
Рассмотрим следующие случаи.
1)
Верхняя сторона Р лежит на верхней стороне прямоугольника А. Для каждой
точки ВХ [Ј] ищем, двигаясь по массиву ВХ вправо и влево от элемента ВХ [i],
такие первые ВХ [ј] и ВХ [К], j<i, k>i, что ВХ [ј, ![]()
![]() [i,
2], ВХ [К,
[i,
2], ВХ [К, ![]() 21.
21.
Считаем, что стороны прямоугольника Pi проходят: нижняя — через точку ВХ [i], левая — через ВХ [ј], правая — через ВХ [К]. Верхняя сторона лежит на верхней стороне А.
Таким образом находим все прямоугольники, примыкающие к верхней стороне.
Прямоугольники, примыкающие к нижней, левой и правой сторонам А, находятся аналогично, но в двух последних случаях надо вместо ВХ использовать массив В У.
2)
Ни одна из сторон Pi не лежит на стороне А. Берем последовательно точки
массива ВУ [i], 1, N, и считаем, что верхняя сторона Pi проходит через точку ВУ
Для этой точки полагаем сначала, что Хведт![]()
![]()
![]() V. При
просмотре массива ВУ вправо от элемента ВУ [i] находим такие точки ВУ [ј] и ВУ
[К], которые первыми удовлетворят условиям ВУ [ј, ВУ[К,
V. При
просмотре массива ВУ вправо от элемента ВУ [i] находим такие точки ВУ [ј] и ВУ
[К], которые первыми удовлетворят условиям ВУ [ј, ВУ[К, ![]() ВУ[ј,
ВУ[ј, ![]() Ц,
ВУ[К,
Ц,
ВУ[К,
(объяснение смотрите ниже), т. е. мы
находим точки с максимальной ординатой, через которые можно провести правую и
левую стороны прямоугольника Н. Внутри интервала (В У [ј, 1]; В У [К, 1]) на
оси Ох ищем точку ВУ [г, 1] такую, что у-координата этой точки ВУ [г, 2]
максимальная, меньше величинь) тах {ВУ [ј, 2], ВУ [К, 2]}. Через эту точку ВУ
[г] проведем нижнюю сторону прямоугольника. Полагаем ХВедгп![]() 1], ХЕп—ВУ
[К, 1].
1], ХЕп—ВУ
[К, 1].
Но этим прямоугольником может не исчерпываться все множество
прямоугольников, у которых точка ВУ [Ј] лежит на верхней стороне. Попытаемся
найти еще один из таких прямоугольников. Очевидно, что левая его сторона имеет
х-координату не меньше чем XBegin, а правая — не больше чем XEnd. Будем искать
такую точку В У [г], что Х Begin [r, ![]() (теперь уже понятно почему), ВУ [r, 2] —
максимальная из всех ординат, меньше тах {В У [ј, 2], ВУ [К, 2]} (мы «сужаем»
прямоугольник как можно незначительнее). Если ВУ [r,
(теперь уже понятно почему), ВУ [r, 2] —
максимальная из всех ординат, меньше тах {В У [ј, 2], ВУ [К, 2]} (мы «сужаем»
прямоугольник как можно незначительнее). Если ВУ [r,![]()
![]() Ц, то это новая левая
сторона, иначе — новая правая. Находим новую нижнюю сторону и т. д. Если мы не
можем найти нового значения ВУ [r], то просмотр прямоугольников с точкой ВУ [il
на верхней стороне закончен, и мы переходим к В У [Н- Ц.
Ц, то это новая левая
сторона, иначе — новая правая. Находим новую нижнюю сторону и т. д. Если мы не
можем найти нового значения ВУ [r], то просмотр прямоугольников с точкой ВУ [il
на верхней стороне закончен, и мы переходим к В У [Н- Ц.
18. Длина стороны первого квадрата — 1, второго — 1, третьего 2, четвертого — З и т. д. Видно, что длины сторон есть числа Фибоначчи, определяемые следующим рекуррентным соотношением:
![]()
Будем хранить координаты четырехугольника Ai ![]() объединения
квадратов с номерами от до Ј.
объединения
квадратов с номерами от до Ј.
Второй квадрат А2 рисуется справа от первого А], Аз — сверху от А2, А4 — слева от Аз, А5 — снизу от А4, А6 — опять справа от А5 и т. д.
Как только точка Р впервые попадает в Д, распечатываем номер
Ј. Проверка принадлежности точки Р четырехугольнику с параллельными сторонами:
пусть левый верхний угол И), правый нижний (х; И); точка Р (Р; Ру) принадлежит
четырехугольнику, если одновременно ![]() и
и![]()
19. Отсортируем координаты точек в порядке неубывания х-координат, а в случае одинаковых х-координат в порядке невозрастания у-координат. Находим координаты средней точки (находящейся в позиции (п div 2+ +1) отсортированного массива координат). Пусть эта точка имеет координаты (хо; И). При этом множество точек оказалось разбитым на З части: точки, лежащие на прямой х— хо; точки, лежащие левее прямой х = Хо; точки, лежащие правее прямой х = хо. Представим, что точки, лежащие левее прямой х = хо, лежат в пределах прямоугольника, х-координата правого края которого равна х: (х1 <хо), а точки, лежащие правее прямой х— хо, лежат в пределах прямоугольника, х-координата левого края которого равна х2 (х— хо). При этом верхний и нижний края обоих прямоугольников имеют координаТЫ утах и соответственно, где утах — максимальная у-координата точек, ymin — минимальная у-координата..
![]() Тогда существует прямая с достаточно
большим углом наклона (например, с углом наклона, тангенс которого превышает
величину (утах—ymin+2)/Z, где Z
Тогда существует прямая с достаточно
большим углом наклона (например, с углом наклона, тангенс которого превышает
величину (утах—ymin+2)/Z, где Z ![]() = min (хо— х»
= min (хо— х» ![]() которая разделяет эти
части. Осталось разделить только точки на прямой так, чтобы количество точек в
получившихся частях было равным (т. е. найти точку пересечения разделяющей
прямой с прямой х— хо). Если количество точек нечетно, то разделяющая прямая проходит
через среднюю точку, иначе — над средней точкой отсортированного массива, но
под предыдущей, если та лежит на прямой х = хо. Таким образом:
которая разделяет эти
части. Осталось разделить только точки на прямой так, чтобы количество точек в
получившихся частях было равным (т. е. найти точку пересечения разделяющей
прямой с прямой х— хо). Если количество точек нечетно, то разделяющая прямая проходит
через среднюю точку, иначе — над средней точкой отсортированного массива, но
под предыдущей, если та лежит на прямой х = хо. Таким образом:
![]() — может быть найдена просмотром массива
х-координат справа налево от средней точки до нахождения первой координаты,
отличной от хо; если такая координата не найдена, то Xl=xo—- 1;
— может быть найдена просмотром массива
х-координат справа налево от средней точки до нахождения первой координаты,
отличной от хо; если такая координата не найдена, то Xl=xo—- 1; ![]() х2 — может
быть найдена просмотром массива х-координат слева направо от средней точки до
нахождения первой координаты, отличной от хо; если такая координата не найдена,
то xt=xo-F 1;
х2 — может
быть найдена просмотром массива х-координат слева направо от средней точки до
нахождения первой координаты, отличной от хо; если такая координата не найдена,
то xt=xo-F 1;
![]() — это у-координата точки, предшествующей
средней точке, если ее х-координата равна хо или равна yo-F 1, если
х-координата точки, предшествующей средней точке, не равна хо.
— это у-координата точки, предшествующей
средней точке, если ее х-координата равна хо или равна yo-F 1, если
х-координата точки, предшествующей средней точке, не равна хо.
![]() После того как хо, И, xt, щ найдены,
осталось написать уравнение прямой с тангенсом угла наклона
После того как хо, И, xt, щ найдены,
осталось написать уравнение прямой с тангенсом угла наклона ![]() проходящей
через точку с координатами (х; У2), определяемую по следующему правилу: если N
— четно,
проходящей
через точку с координатами (х; У2), определяемую по следующему правилу: если N
— четно,
то Ь— хо; ![]() иначе Х2=Хо; У2=Уо•
иначе Х2=Хо; У2=Уо•
20. Проведем через каждую вершину этих двух выпуклых многоугольников прямые, параллельные оси Оу. Эти прямые разбивают всю плоскость на полосы. Пересечение каждой полосы с выпуклым многоугольником образует трапецию, поэтому внутри каждой полосы пересечением двух выпуклых многоугольников будет пересечение двух четырехугольников. Собираем все эти пересечения в одну фигуру, удаляя при этом ложные вершины, которые возникают на границах между полосами.
Объединение делается аналогично.
21. Если проекция точки Z попадает на сторону многоугольника, а не на ее продолжение, то минимальное расстояние от точки Z до стороны есть длина проведенного перпендикуляра. Если же проекция точки Z попадает на продолжение стороны, то минимальное расстояние есть минимум из расстояний от Z до концевых точек этой стороны.
Минимальное расстояние от гочки Z до контура есть минимум из расстояний от точки Z до каждой из сторон.
22. Проверяем, лежит ли точка Z на каком-либо отрезке. Если нет, то проводим отрезок, концевые точки которого Z, и, например, точка с номером 1. Находим ближайшую к Z точку пересечения этого отрезка и сторон многоугольников, на которые разбивается плоскость. Пусть эта точка принадлежит стороне АЬ. Для треугольника ZAB сначала определим направление обхода контура от А к В (задача З). Для стороны АВ ищем следующую, смежную с ней, сторону ВС контура, которая образует максимальный по величине угол с отрезком ВА
Рис. 27
(угол отсчитывается от отрезка АВ по часовой или против часовой стрелки в зависимости от того, по или против часовой стрелки обход). Находим замкнутый контур и определяем, находится точка Z внутри него или снаружи; если снаружи, то удаляем из фигуры все ребра этого контура и повторяем процесс (рис. 27).
23.
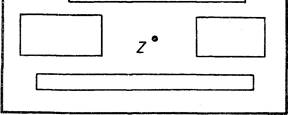 |
24, Дадим другую интерпретацию этой задачи: есть
N отрезков, описываемых уравнениями
![]()
![]()
Предположим, что отрезки не совпадают.
1) Найти верхний
контур объединения фигур ![]() bi<y, 1
bi<y, 1![]()
(т. е. найти такую разбивку to, ..., tp отрезка [хо,
ха и те кусочки отрезков![]()
![]() 0 Р—1, что отрезок
qx+bi лежит не ниже
0 Р—1, что отрезок
qx+bi лежит не ниже ![]() любого другого отрезка при
любого другого отрезка при![]()
2) HaiTH TaKYIO pa36HBKY 0Tpe3Ka [XO, Xi] TOAKaMH S],
I-ITO B Ka>KAOM ceKTope ![]() i +1 KYCOYKH 0Tpe3KOB bi,
I N He nepeceKaK)Tcfl, a Ha rpaHH1.1ax ceKTopa, x=Si H x=Si+l, JIOKHT no
i +1 KYCOYKH 0Tpe3KOB bi,
I N He nepeceKaK)Tcfl, a Ha rpaHH1.1ax ceKTopa, x=Si H x=Si+l, JIOKHT no
KpaüHeii Mepe 110 0AH0i T0HKe
nepeceqeHHH ompe3KOB bi, i = l,![]()
Peu.1HM cl--raqajla nyHKT 2) 3amaYH, 3aTeM IIYHKT 1). Hafime.M BCe nepeceqeHHfl OTPe3KOB aiX+ bi, i= l,
![]() N, Apyr C mpyroM. A06aBHM B STO
MHO>KeCTBO TO t1KH XO H X!. YnopHmoz-1HM TOMKH
nepeceqeHHf1 no B03paCTaHH10 (ecJIH B 110CJ1eAOBaTeJ1bHOCTH BCTpeqaK)Tcfl
HeCKOJ1bKO ToqeK C OAHHM H TelM xe 3HaqeHHeM, 'ro OCTaBJ151eM H3 HUX TOJ1bKO
OAHY). 110J1yqaeM rraKHM 06pa30M noc,neÅOBaTeJ1bHOCTb s SQ.
N, Apyr C mpyroM. A06aBHM B STO
MHO>KeCTBO TO t1KH XO H X!. YnopHmoz-1HM TOMKH
nepeceqeHHf1 no B03paCTaHH10 (ecJIH B 110CJ1eAOBaTeJ1bHOCTH BCTpeqaK)Tcfl
HeCKOJ1bKO ToqeK C OAHHM H TelM xe 3HaqeHHeM, 'ro OCTaBJ151eM H3 HUX TOJ1bKO
OAHY). 110J1yqaeM rraKHM 06pa30M noc,neÅOBaTeJ1bHOCTb s SQ.
AJIH Ka>KÄoro 0Tpe3Ka [S],
Sj+l], i![]() Q — l HaxoAHM ero cepeAHHY
Q — l HaxoAHM ero cepeAHHY ![]() BblqHCJIHeM 3HaqeHHfl
BblqHCJIHeM 3HaqeHHfl ![]() N, copTHpyeM ux 110
BOapaCTaHHIO.
N, copTHpyeM ux 110
BOapaCTaHHIO.
HHÅeKCb1 i 3HaqeHMÜ B OTCOPTMPOBaHHOÜ 110CJ1eAOBaTeJ1bHOCTU AJ1fl QHKCUPOBaHHOPO j KaK pa3 H eCTb HCKOMaH nepecTaH0BKa (ill, i2j, . . . , iNi) quce,n 1, 2, 3, N, yr10M%HYTafl B 4)OPMYJIHPOBKe 3amaqu B nyHKTe 2 0Tpe3Ka
![]()
AJIH peweHMfl TlYHKTa I BbUIUU1eM no nopqÅKY ![]() Ka»uoro 0Tpe3Ka [Si, S/ +1],
Ka»uoro 0Tpe3Ka [Si, S/ +1], ![]() Q— l, Bej1HMHHb1 iNj (3T0
HHÅeKC caMoro BepxHero 0Tpe3Ka B ceKTope [S], S. +1]).
Q— l, Bej1HMHHb1 iNj (3T0
HHÅeKC caMoro BepxHero 0Tpe3Ka B ceKTope [S], S. +1]).
OTpe30K C HOMePOM k MO>KeT 651Tb caMb1M BePXHHM
HeCKOJ1bKHX CMeXHb1X ceKTOPOB [S S ] N03TOMY Mbl npocMa rrpHBaeM H0Mepa iNf,
0Tpe3KaM [Sj, Si+ll, j![]() Q— l, H onpeAeJIHeM mocnemoBateJ1bHb1e
MaKCHMaJ1bHb1e OTPe3KH, [10MeqeHHb1e OAHHM H TeM xe HOMePOM. KOHL1eBb1e TOMKM
3THX MaKCHMaJ1bHb1X OTPe3KOB H eCTb MCKOMb1e TOMKU t t (OHM Bb16npakOTCfl no
YKagaHHOMY Bblll-le MeTOAY H3 'roqeK So, SQ).
Q— l, H onpeAeJIHeM mocnemoBateJ1bHb1e
MaKCHMaJ1bHb1e OTPe3KH, [10MeqeHHb1e OAHHM H TeM xe HOMePOM. KOHL1eBb1e TOMKM
3THX MaKCHMaJ1bHb1X OTPe3KOB H eCTb MCKOMb1e TOMKU t t (OHM Bb16npakOTCfl no
YKagaHHOMY Bblll-le MeTOAY H3 'roqeK So, SQ).
![]() 25. flycTb B (burype yxe f]POBemeHb1
L Anarolda.,qei, H OHM pa36HBaK)T n-yrOJ1bHMK Ha K qacTei. Ml)0BemeM eme OAHY
(L+ I)-K) nuanOHaJ1b. FlomcYHTaeM, CKOJ1bKO paHee 11POBeÅeHHb1X
muaP0HaJ1eä nepeceKaeT BO BHYTPeHHHX Toq-
25. flycTb B (burype yxe f]POBemeHb1
L Anarolda.,qei, H OHM pa36HBaK)T n-yrOJ1bHMK Ha K qacTei. Ml)0BemeM eme OAHY
(L+ I)-K) nuanOHaJ1b. FlomcYHTaeM, CKOJ1bKO paHee 11POBeÅeHHb1X
muaP0HaJ1eä nepeceKaeT BO BHYTPeHHHX Toq-
ках эта диагональ. Обозначим количество
пересечений ![]() через S. Проведение диагонали:
через S. Проведение диагонали:
1) увеличивает количество разбивок п-угольника на 1;
2) каждое пересечение этой диагонали с ранее проведенной диагональю также увеличивает количество разбивок на 1 (по условию никакие З диагонали не пересекаются в одной точке).
Итак, после проведения (L+ 1)-й диагонали количество частей станет k+S+l (предполагается, что (L+ 1)-я диагональ не совпадает ни с одной ранее проведенной).
Как определить, пересекается ли диагональ, соединяющая вершины i и ј, с диагональю, заданной вершинами т и р? Вершины i и ј разбивают контур многоугольника на 2 части: множество А — вершины, лежащие на контуре между вершинами i и ј, и множество В — вершины контура между и i (множества А и В не включают i и ј). Если т принадлежит одному из этих множеств, а р — другому, то диагонали пересекаются, иначе — нет.
26. Будем обозначать через Vi вершину ломаной с координатами (хо И).
Сначала рассмотрим разрез круга ломаной, состоящей только из
двух ребер ![]() Щ) и
Щ) и ![]() V3). Для того чтобы
разнять этот круг, необходимо тянуть в направлении вектора S, выходящего из
точки V2 и лежащего либо внутри угла Vl V2V3 (вершина угла — точка Щ), либо внутри
центрально-симметричного ему относительно точки V2 угла. Будем говорить, что
вектор S лежит в конусе С2 с вершиной V2.
V3). Для того чтобы
разнять этот круг, необходимо тянуть в направлении вектора S, выходящего из
точки V2 и лежащего либо внутри угла Vl V2V3 (вершина угла — точка Щ), либо внутри
центрально-симметричного ему относительно точки V2 угла. Будем говорить, что
вектор S лежит в конусе С2 с вершиной V2.
Аналогично, если ломаная определяется К вершинами, то
для каждой пары ребер (V• И ) и (V • V )![]()
![]() К—2, определяем конус Ci+l возможных
направлений перемещения, затем считаем, что параллельным переносом вершины всех
конусов совмещены в одной точке. Пересечение всех Ci,
К—2, определяем конус Ci+l возможных
направлений перемещения, затем считаем, что параллельным переносом вершины всех
конусов совмещены в одной точке. Пересечение всех Ci, ![]() К— 1, и даст искомое
возможное направление разнимания круга. Если это пересечение пусто, то круг
разнять нельзя, иначе
К— 1, и даст искомое
возможное направление разнимания круга. Если это пересечение пусто, то круг
разнять нельзя, иначе ![]() можно.
можно.
27. Пусть
точка Z — центр координат (если это не так, сделаем параллельный перенос). Для
того чтббы звено забора было полностью видно, необходимо и достаточно, чтобы из
точки Z, где стоит человек, были видны обе вершины этого звена и еще
какая-нибудь его внутренняя точка. Будем считать, что вершина Р звена видна,
если интервал (Z; Р) не пересекает никаких звеньев забора или же если обе
концевые вершины пересекаемого звена К лежат на [Z; Р], т. е. человек смотрит
вдоль звена К.![]()
![]() Отсортируем по
неубыванию углы, образуемые с осью Ох отрезками, одна концевая точка которых Z,
а вторая пробегает все вершины звеньев (углы отсчитываются от точки Z в
положительном направлении,
Отсортируем по
неубыванию углы, образуемые с осью Ох отрезками, одна концевая точка которых Z,
а вторая пробегает все вершины звеньев (углы отсчитываются от точки Z в
положительном направлении, ![]() т. е. против часовой стрелки). Получаем
последовательность углов щ, щ, . . . , ап. Добавляем в эту последовательНОСТЬ
угол щ. Из точки Z в направлении между прямыми, идущими под углами ai и ai+l,
может быть виден кусок только одного единственного звена.
т. е. против часовой стрелки). Получаем
последовательность углов щ, щ, . . . , ап. Добавляем в эту последовательНОСТЬ
угол щ. Из точки Z в направлении между прямыми, идущими под углами ai и ai+l,
может быть виден кусок только одного единственного звена.
Из точки Z под углами (щ-4- ai+l)/2, 1 п, проводим лучи и для
каждого луча смотрим, какое звено К этот луч пересекает первым (пересечение по
вершине не учитывается). В том случае, если у этого звена К видны ![]() обе вершины,
то звено видно полностью, если хотя бы одна вершина не видна, то К видно
частично.
обе вершины,
то звено видно полностью, если хотя бы одна вершина не видна, то К видно
частично. ![]()
После анализа точек пересечения всех п лучей те звенья, которые не видны ни полностью, ни частично, получают пометку невидимых.
![]() 28. Рассматриваем номера граней как
элементы массивов. Сортируем каждый из массивов с помощью некоторого обменного
алгоритма (например, с помощью «пузырьковой» сортировки), подсчитывая
количество обменов (пусть это kN и КМ соответственно). Если отсортированные
массивы совпадают и (КМ— КМ) кратно 2, то тетраэдры совпадают. (Обмен двух
граней можно трактовать как отражение тетраэдра в зеркале.)
28. Рассматриваем номера граней как
элементы массивов. Сортируем каждый из массивов с помощью некоторого обменного
алгоритма (например, с помощью «пузырьковой» сортировки), подсчитывая
количество обменов (пусть это kN и КМ соответственно). Если отсортированные
массивы совпадают и (КМ— КМ) кратно 2, то тетраэдры совпадают. (Обмен двух
граней можно трактовать как отражение тетраэдра в зеркале.) ![]()
З Информатика, 8—9 кл.
Глава 2. ПОИСК И СОРТИРОВКИ
1. ПОСЛЕДОВАТЕЛЬНЫЙ ПОИСК
НЕОБХОДИМОГО ЭЛЕМЕНТА В МАССИВЕ![]()
Человеку постоянно приходится сталкиваться с задачами поиска
требуемой информации. Типичными примерами может служить работа с тем или иным
справочни![]() ком, телефонной книгой, библиотечной
картотекой.
ком, телефонной книгой, библиотечной
картотекой.
В программировании поиск является одной из наиболее часто выполняемых операций. Будем считать, что множество из N элементов задано в виде массива (таблицы) А [l..N].
Среди разновидностей простейших задач поиска, встречающихся на практике, можно выделить следующие типы:
1.
Найти хотя бы один элемент, равный заданному ![]() элементу Х. В
результате необходимо получить 1— индекс (номер) элемента массива такой, что А
элементу Х. В
результате необходимо получить 1— индекс (номер) элемента массива такой, что А![]()
2.
Найти все элементы, равные заданному Х. В результате необходимо получить
количество таких элементов и (или) их индексы. ![]()
Иногда поиск организуется не по совпадению с элементом Х, а по
выполнению некоторых условий. Примером может служить поиск элементов,
удовлетворяющих условиям ХК А ![]() где Щ и Х2 \заданы'.
где Щ и Х2 \заданы'.
Если у нас нет никакой добавочной информации о разыскиваемых данных, то очевидный подход — это последовательный просмотр массива. Такой метод называется линейным или последовательным поиском.
Рассмотрим сначала реализацию последовательного поиска для задач типа 1.
Поиск заканчивается при выполнении одного из двух следующих условий:
![]()
1.
Элемент найден, т. е. в массиве есть такой элемент А [i], что А![]()
2. Весь массив просмотрен и совпадения не обнаружено.
Одним из возможных решений данной задачи может быть следующее: пусть Р — переменная логического типа, которая имеет значение «истина», если элемент в массиве найден, и «ложь» — в противном случае.
р : «Ложь» нц для i от I до N
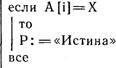
кц
Если после выполнения алгоритма Р = «Истина», то элемент найден, если переменная Р не изменила своего значения, то элемента нет.
Часто требуется не только определить, есть ли в массиве искомый элемент, но и установить, на каком месте он находится. Будем хранить индекс найденного элемента в переменной К:
нц для i от 1 до N
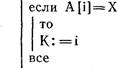
кц
После выполнения данного алгоритма по значению переменной К можно определить, есть ли в массиве искомый элемент, и если есть, то где он стоит. Если в массиве несколько таких элементов, то в переменной К будет храниться номер последнего из них. Если такого элемента нет, то значение переменной К не изменится (останется равным нулю).
![]()
На практике операцию поиска приходится выполнять достаточно часто, и скорость работы программы находится в прямой зависимости от используемого алгоритма поиска.
В рассмотренных выше алгоритмах требуется просмотреть весь массив даже в том случае, если искомый элемент находится в массиве на первом месте.
Для сокращения времени поиска можно останавливаться сразу после того, как элемент найден. В этом случае весь массив придется просмотреть только тогда, когда искомый элемент последний или его нет вообще. В результате получим следующий алгоритм:
i: = l ![]() нц пока и
нц пока и![]()
Цикл заканчивает работу, либо когда будет найден искомый элемент, либо когда i=N-Fl (элемента, совпадающего с Х, не существует).
На каждой итерации цикла требуется
увеличивать индекс i и вычислять логическое выражение. Давайте попытаемся
ускорить поиск, упростив логическое выражение. Поместим в конец массива
дополнительный элемент со значением Х. Тогда совпадение с Х обязательно
произойдет, и мы можем отбросить проверку условия (А >Х). Такой
вспомогательный элемент часто на![]() зывают «барьером» или «часовым», так как
он препятствует выходу за пределы массива. В исходнђм массиве теперь будет N+l
элемент.
зывают «барьером» или «часовым», так как
он препятствует выходу за пределы массива. В исходнђм массиве теперь будет N+l
элемент.
Алгоритм поиска с «барьером» выглядит следующим образом: A[N+ll: = Х
![]()
кц
Если по выходу из цикла i=N+l (Х равен «барьеру»), то
элемента Х в массиве А [l..N] нет. ![]()
Для реализации поиска в задачах типа 2 (нахождение количества элементов, равных Х) в любом случае придется просматривать весь массив.
Если требуется определить количество
элементов, то заводят переменную, значение которой увеличивают на ![]() каждый раз,
когда найден нужный элемент. Такую
каждый раз,
когда найден нужный элемент. Такую ![]() переменную называют «счетчиком». До
начала просмотра элементов массива «счетчику» нужно задать начальное значение
или, другими словами, инициализировать значение переменной. В данном случае это
начальное значение равно нулю. Алгоритм подсчета элементов, равных заданному,
составьте самостоятельно.
переменную называют «счетчиком». До
начала просмотра элементов массива «счетчику» нужно задать начальное значение
или, другими словами, инициализировать значение переменной. В данном случае это
начальное значение равно нулю. Алгоритм подсчета элементов, равных заданному,
составьте самостоятельно.
![]()
Для получения индексов искомых элементов создадим новый массив В [l..N]. Как только будет найден необходимый элемент, его индекс будет заноситься в массив В. В переменной К будет храниться номер последнего занятого места в массиве В. Сначала К —0.

После завершения работы первые К элементов массива В будут содержать индексы искомых элементов.
Вопросы для повторения
1. Что называют последовательным поиском?
2. Как определить, что в массиве был найден элемент?
З. Какой из алгоритмов (2.2), (2.3) или (2.4) работает быстрее и почему?
4. Что такое поиск с «барьером»?
5. Для чего используют переменные «счетчики»?
6. Что такое инициализация переменной?
S 2. ПОИСК МАКСИМАЛЬНОГО И МИНИМАЛЬНОГО ЭЛЕМЕНТОВ В МАССИВЕ
![]() Очень часто для решения задачи требуется
находить не заданный элемент массива, а максимальный (наибольший) или
минимальный (наименьший) элемент.
Очень часто для решения задачи требуется
находить не заданный элемент массива, а максимальный (наибольший) или
минимальный (наименьший) элемент.
Рассмотрим задачу нахождения максимального элемента. Если в массиве один единственный элемент, то он и есть максимальный. В противном случае воспользуемся тем, что максимальным в массиве из i элементов является максимум из A [i] и максимального среди первых i-l элементов.
тах: = А [1] нц для i от 2 до N
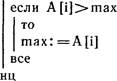
После завершения работы в переменной тах будет храниться значение максимального элемента массива. Однако данный алгоритм не позволяет определить, на каком месте в массиве находится этот максимальный элемент. Будем использовать перменную К для хранения индекса максимального элемента.
нц для i от 2 до N
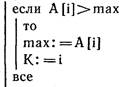
кц
После выполнения алгоритма переменная К будет содержать значение индекса максимального элемента.
![]()
Если в массиве несколько элементов имеют
максимальное значение, то в переменной К будет запоминаться индекс первого из
них. Если использовать условие А ![]() то будет запоминаться индекс последнего
из максимальных.
то будет запоминаться индекс последнего
из максимальных.
Для поиска минимального элемента необходимо заменить знак
> в ЕСЛИ на знак![]()
Вопросы для повторения
1. Какой элемент массива является максимальным, какой — минимальным?
Х Как найти максимальный элемент в
массиве? Как найти минимальный элемент в массиве?![]()
З. Как определить номер первого элемента, равного максимальному?
4. Как определить номер последнего
элемента, равного минимальному? ![]()
S З. УПОРЯДОЧЕНИЕ ЭЛЕМЕНТОВ МАССИВА
Сортировка массива — это расстановка элементов массива в некотором порядке. В отсортированном массиве, за счет предварительно выполненной работы по упорядочению, поиск элемента (даже в худшем случае) можно осуществлять, не просматривая весь массив. Пример отсортированного массива — это, например, список телефонов в справочнике, список фамилий в адресной книге и т. д.
![]() Примером задачи сортировки может служить
следующая: в массиве из N различных чисел необходимо осуществить их
перестановку так, чтобы после нее в массиве первым элементом было самое большое
число. Каждое следующее должно быть меньше предыдущего, а последнее — самое
маленькое из чисел данного массива. Такой порядок расположения чисел называют
убывающим.
Примером задачи сортировки может служить
следующая: в массиве из N различных чисел необходимо осуществить их
перестановку так, чтобы после нее в массиве первым элементом было самое большое
число. Каждое следующее должно быть меньше предыдущего, а последнее — самое
маленькое из чисел данного массива. Такой порядок расположения чисел называют
убывающим.
Если в массиве есть равные числа, то задачу можно переформулировать следующим образом: в массиве из N чисел осуществить их перестановку так, чтобы после перестановки в массиве первым элементом было самое большое число. Каждое следующее должно быть не больше предыдущего, а последнее— самое маленькое из чисел данного массива. Такой порядок расположения чисел называют невозрастающим.
Порядок, при котором в массиве первым элементом является самое маленькое число, каждое следующее число больше предыдущего, а последнее — самое большое из чисел данного массива называют возрастающим.
Если в массиве есть равные числа и они расположены так, что первым элементом является самое маленькое число, каждое следующее число не меньше предыдущего, а последнее— самое большое из чисел данного массива, то такой порядок называют неубывающим.
![]()
![]() Задача сортировки, как и любая другая задача, может
решаться множеством способов, каждый из которых имеет как достоинства, так и
недостатки. Выбор способа сортировки определяется особенностями решаемой
задачи.
Задача сортировки, как и любая другая задача, может
решаться множеством способов, каждый из которых имеет как достоинства, так и
недостатки. Выбор способа сортировки определяется особенностями решаемой
задачи.
При выборе метода сортировки необходимо учитывать объем требуемой памяти и скорость работы. При сортировке массива желательно использовать как можно меньше дополнительной памяти, поэтому обычно рассматриваются алгоритмы, которые упорядочивают массив перестановками его элементов (без использования еще одного массива). Оценить скорость работы метода сортировки можно, оценив количество требуемых операций сравнения и (или) операций перестановок Элементов.
Ниже рассматриваются методы сортировки линейного массива по убыванию (невозрастанию). Сортировка по возрастанию (неубыванию) производится аналогично.
3.1. Сортировка выбором![]()
Давайте представим, что перед нами поставлена задача расставить N чисел по убыванию. Как бы мы ее решали?
Наверное, пришлось бы сначала найти максимальное из всех чисел и поменять местами с первым числом. Затем из еще неотсортированных элементов надо было бы опять выбрать максимальный элемент и поменять местами с первым элементом из еще не отсортированной части.
Примененный нами метод и называется сортировкой выбором. ![]()
Формально его можно описать следующим образом. На i-M шаге
(i=l, ![]() выбираем из элементов с индексами от i до
N максимальный элемент; меняем местами найденный максимальный и элемент А [i];
на i-M месте оказывается максимальный элемент из еще неотсортированной части
массива.
выбираем из элементов с индексами от i до
N максимальный элемент; меняем местами найденный максимальный и элемент А [i];
на i-M месте оказывается максимальный элемент из еще неотсортированной части
массива.![]()
После выполнения М— 1-го шага в позиции А [N] будет находиться самый маленький элемент массива.
Название метода, «сортировка выбором» определяется тем, что на каждом шаге мы находим (выбираем) максимальный элемент из еще неотсортированной части массива.
![]() Запишем алгоритм сортировки выбором:
Запишем алгоритм сортировки выбором:
 нц для i от до
нц для i от до![]()
нц для ј от i +1 до N тах
кц
Внутренний цикл ДЛЯ ј ОТ i+l ДО N является ничем иным, как
алгоритмом поиска максимального алгоритма среди элементов с номерами от i+ l до
N. Рассмотрим работу данного метода на массиве А— ![]() 4, З, 6, 5}.
Максимальный элемент будем подчеркивать.
4, З, 6, 5}.
Максимальный элемент будем подчеркивать.

Подсчитаем количество сравнений, которые пришлось сделать для упорядочения массива.
На первом шаге для нахождения максимального элемента
необходимо (N— 1) сравнение, на втором (N—2), на третьем (N—3) на последнем
шаге одно срав![]() нение. Найдем сумму:
нение. Найдем сумму:
![]() 1 = N (М— 1 —(N2 — N)/2.
1 = N (М— 1 —(N2 — N)/2.![]()
П р и м е ч а н и е. Сумму можно посчитать исходя из следующих соображений. Количество слагаемых равно (N— 1), сумма первого и последнего, второго и предпоследнего и т. д. равна N. Произведение N (N—l) даст удвоенную сумму, так как каждое слагаемое будет входить в эту сумму дважды, поэтому его нужно разделить на 2.
![]() Количество перестановок элементов равно
(N— 1). Это количество определяется внешним циКлом ДЛЯ.
Количество перестановок элементов равно
(N— 1). Это количество определяется внешним циКлом ДЛЯ.
3.2. Сортировка обменом![]()
Рассмотрим еще один метод сортировки, который формально можно описать так:
На i-M шаге (i=l N 1) выполняем:
1. Сравниваем первые два элемента. Если первый меньше второго, то меняем их местами.
2. Сравниваем
второй и третий, третий и четвертый, ![]() N—i и N—i+ 1, при необходимости меняя
элементы местами. Самый маленький окажется на i-M месте в массиве.
N—i и N—i+ 1, при необходимости меняя
элементы местами. Самый маленький окажется на i-M месте в массиве. ![]()
После первого шага самый маленький элемент массива помещается на N-e место. Массив будет отсортирован после просмотра, в котором участвуют только первый и второй элементы.
Название метода «сортировка обменом» определяется тем, что алгоритм основывается на обмене местами двух элементов массива.
Описанный метод сортировок обменом называют также пузырьковой сортировкой.
Алгоритм
метода сортировки обменом: ![]()
нц для i от 1 до N—l 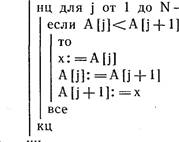 нц
для ј от 1 до N—i
нц
для ј от 1 до N—i
кц
Рассмотрим
его на примере гого же массива А 1 ![]()

Число сравнений в данном алгоритме равно также
![]()
При каждом сравнении возможна перестановка двух элементов в массиве. Поэтому количество перестановок (в худшем случае) будет равно количеству сравнений,
![]()
* На последних двух проходах в приведенном выше примере массив не менялся. Заметим, что если на каком-то шаге алгоритма элементы массива уже упорядочены, то при последующих проходах по массиву перестановки больше выполняться не будут. Следовательно, как только количество выполненных на последнем проходе перестановок станет равным 0, алгоритм можно заканчивать.
Если запоминать положение (индекс) К последнего обмена, то все пары соседних элементов дальше индекса К уже находятся в желаемом порядке. Поэтому на следующем проходе просмотр можно заканчивать на индексе К.
Р:
= «Истина» ![]()
![]()
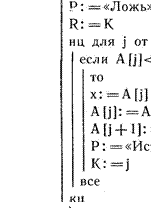
![]() В приведенном фрагменте переменная Р
логического типа используется для определения, были перестановки или нет, а
переменная К — для хранения индекса по-
В приведенном фрагменте переменная Р
логического типа используется для определения, были перестановки или нет, а
переменная К — для хранения индекса по-
следнего обмена. Переменная R является границей, на которой заканчивается просмотр.
Если проанализировать пузырьковую сортировку, то можно
заметить, что самое маленькое число занимает свое место за один проход по
массиву, а самое большое перемещается по направлению к своему месту на одну
позицию при каждом проходе. Это наводит на мысль ![]() чередовать направление
проходов. Такая сортировка называется шейкер-сортировкой. Рассмотрим ее работу
на том же массиве А
чередовать направление
проходов. Такая сортировка называется шейкер-сортировкой. Рассмотрим ее работу
на том же массиве А ![]() 5}. (L — левая граница просмотра, R —
правая.)
5}. (L — левая граница просмотра, R —
правая.)

Алгоритм данной сортировки попытайтесь написать самостоятельно.
Все эти улучшения сокращают количество операций сравнения для частных случаев, однако при неблагоприятной начальной расстановке элементов массива (подумайте какой) приходится проделать все (N2 —N)/2 операции сравнения*.
Вопросы для повторения
1. На каких принципах основана сортировка выбором?
![]() 2. На каких принципах основана
сортировка обменом?
2. На каких принципах основана
сортировка обменом?
З. За какое количество операций сравнения будет отсортирован массив, если применять сортировку обменом? сортировку выбором?
4. Сколько перестановок будет сделано для упорядочения массива, если применять сортировку обменом? сортировку выбором?
5.
Как можно
сократить время работы алгоритма сортировки обменом? ![]()
6. Алгоритм какой из сортировок будет работать быстрее? Почему?
![]() S 4. СОКРАЩЕНИЕ
ОБЛАСТИ ПОИСКА. двоичный ПОИСК
S 4. СОКРАЩЕНИЕ
ОБЛАСТИ ПОИСКА. двоичный ПОИСК
Рассмотрим следующую задачу.
В отделение милиции аэропорта поступило сообщение о том, что некто пытается провезти на самолете бомбу. Диверсант пока находится в здании аэропорта. Допустим, что в нашем распоряжении имеется прибор, который может определить, есть ли бомба в комнате. Необходимо как можно быстрее определить, у кого находится бомба.
Самым простым (и самым продолжительным по времени) решением будет последовательная проверка каждого из пассажиров в комнате с прибором. Однако такой подход вряд ли поможет сэкономить время.
![]() Поступим по-другому. Разделим всех пассажиров на две
наиболее равные по численности группы. Разведем группы по двум комнатам. Прибор
смо>кет определить, в какой из комнат находится бомба. В результате такого
действия количество подозреваемых уменьшится вдвое. С оставшимися
подозреваемыми поступим аналогичным образом: разделим их на 2 части и разведем
по двум комнатам. При этом опять количество подозреваемых сократится.
Продолжаем так, пока не найдем диверсанта.
Поступим по-другому. Разделим всех пассажиров на две
наиболее равные по численности группы. Разведем группы по двум комнатам. Прибор
смо>кет определить, в какой из комнат находится бомба. В результате такого
действия количество подозреваемых уменьшится вдвое. С оставшимися
подозреваемыми поступим аналогичным образом: разделим их на 2 части и разведем
по двум комнатам. При этом опять количество подозреваемых сократится.
Продолжаем так, пока не найдем диверсанта.
Такой метод поиска называется двоичным поиском. Встречаются и
другие названия этого метода: бинарный поиск, логарифмический поиск, метод
Деления пополам,![]()
ДИХОТОМИЯ.
В программировании такой поиск применяют для нахождения элемента Х в отсортированном массиве.
Пусть массив отсортирован в порядке убывания. Находим средний
элемент массива А [т] (т— div (N+ 1, 2) и сравниваем его с элементом Х. Если он
равен Х, то поиск заканчивается. Если он меньше Х, то все элементы с индексами,
большими или равными т, можно не рассматривать: если же он больше Х, то
исключаются элементы с индексами, меньшими или равными т.![]()
При выполнении данного алгоритма нам придется на каждом шаге пересчитывать границы поиска. Так, на первом шаге левая граница L=l, правая — R=N. На втором шаге либо левая, либо правая граница поменяет свое значение.
![]() Поиск будет
продолжаться до тех пор, пока элемент
Поиск будет
продолжаться до тех пор, пока элемент ![]() не будет найден, либо когда левая и правая
границы поиска не совпадут, что соответствует отсутствию элемента в массиве.
не будет найден, либо когда левая и правая
границы поиска не совпадут, что соответствует отсутствию элемента в массиве.
Пусть натуральное число К есть количество операций сравнения, которые необходимы для нахождения элемента в упорядоченном массиве методом дихотомии. Число К определяется из следующего неравенства: N<2 k, причем К — минимальное из всех возможных.
Примеча н и е. Обычно в математике для определения
числа К пользуются функцией 10g 1 . Тогда число К будет вычислено по
форму![]() ле
ле ![]() /V]+ 1, где квадратные скобки обозначают целую часть числа, находящегося
в скобках.
/V]+ 1, где квадратные скобки обозначают целую часть числа, находящегося
в скобках.
![]()
![]() Алгоритм
имеет следующий вид:
Алгоритм
имеет следующий вид: ![]()
![]()
Р: = «ложь» 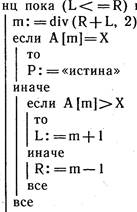 нц пока = R
) и (Р==«ложь»)
нц пока = R
) и (Р==«ложь»)
кц
![]() то 10Д2 b=a.
то 10Д2 b=a.
После выполнения алгоритма в переменной т будет храниться номер найденного элемента, если он есть в массиве (Р = «истина»).
При мер. В массиве А найти элемент х:
![]()
![]() 4>l; Р=
«ложь»
4>l; Р=
«ложь»
Р= «ложь»![]()
Р= «истина»
![]()
![]() Р= «ложь»
Р= «ложь»
Р= «ложь» Р= «ложь»
Р= «ложь»
Р= «ложь»
![]()
![]() Р «ложь»
Р «ложь»
Р= «ложь»
Р= «истина»
Можно несколько сократить запись алгоритма, если как и в случае линейного поиска попытаться упростить составное условие цикла ПОКА.

если ![]() то
то
Р: ==«истина» иначе
Р: = «ложь» все
После выполнения цикла к переменной R хранится номер
элемента, равного Х, если такой элемент в массиве есть. Если элемента нет, то
переменная R показывает номер места в массиве, куда можно вставить элемент Х,
не нарушая упорядоченности массива.![]()
![]() Вопросы для повторения
Вопросы для повторения
1. В каких случаях можно использовать метод двоичного поиска? Приведите примеры из жизни.
2. В чем суть метода двоичного поиска?
З. Почему алгоритм (2.12) будет
работать быстрее, чем алгоритм (2,11)? ![]()
S ДРУГИЕ ВИДЫ СОРТИРОВОК
Все сортировки, рассмотренные раньше, требуют (N2 —N)/2 операций сравнения, или, другими словами, порядка N2 операций. Используя дихотомический поиск, количество операций сравнения можно сократить.
5.1. Сортировка вставками
Будем просматривать элементы массива А, начиная со
второго. Каждый новый элемент А [i] будем вставлять на подходящее место в уже
упорядоченную совокупность ![]()
![]() 1]. Это место определяется
последовательными сравнениями элемента А [Г] с упорядоченными элементами А [1],
1]. Это место определяется
последовательными сравнениями элемента А [Г] с упорядоченными элементами А [1],
![]() ц.
ц.
Такой метод сортировки называется сортировкой простыми вставками. Он также требует порядка N 2 операций сравнения и столько же перестановок элементов в массиве. Попытайтесь составить алгоритм метода самостоятельно.
Если для поиска места элемента А [i] в упорядоченную совокупность А [1] А [i— 1] воспользоваться методом двоичного поиска, то количество операций сравнения будет порядка N log2 N, что существенно меньше чем N2. Количество же перестановок будет порядка АР. Такой метод сортировки называется сортировкой бинарныжи вставками.
Алгоритм сортировки бинарными вставками:
нц для i от 2 до N
![]()
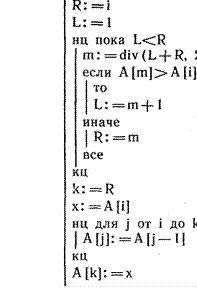 (2.13)
(2.13)
кц
![]() цикл ПОКА — цикл поиска места вставки. Он основан на
методе двоичного поиска. (Сравни с алгоритмом 2.12.) цикл ДЛЯ ОТ i ДО k+l ШАГ—
1 сдвигает элементы для освобождения места вставки. Пример. (Элемент, который
вставляем, подчеркнут.) 1. 1,
цикл ПОКА — цикл поиска места вставки. Он основан на
методе двоичного поиска. (Сравни с алгоритмом 2.12.) цикл ДЛЯ ОТ i ДО k+l ШАГ—
1 сдвигает элементы для освобождения места вставки. Пример. (Элемент, который
вставляем, подчеркнут.) 1. 1,
з.
4. 9,

5.2. Сортировка слияниями
Сначала рассмотрим следующую задачу:
Есть два отсортированных в порядке невозрастания массива А [l..N] и В [l..M]. Получить отсортированный по невозрастанию массив C [1..N+M], состоящий из элементов массивов А и В («слить» вместе массивы А и В).
Можно в массив С записать сначала элементы массива А, затем
массива В, затем применить любой алгоритм ![]() сортировки. Но в этом
случае мы не используем того, что А и В уже отсортированы. Будем просматривать
элементы массивов А и В, начиная с А [1] и В [1]. Если, например, А [1], то
C[l]: = А [Ц, и на следующем шаге сравниваем уже А [2] и В [1], занося больший
элемент пары в ячейку С [2], и т. д. Запись алгоритма:
сортировки. Но в этом
случае мы не используем того, что А и В уже отсортированы. Будем просматривать
элементы массивов А и В, начиная с А [1] и В [1]. Если, например, А [1], то
C[l]: = А [Ц, и на следующем шаге сравниваем уже А [2] и В [1], занося больший
элемент пары в ячейку С [2], и т. д. Запись алгоритма:
![]() : текущие индексы в массивах А,
: текущие индексы в массивах А,![]()
если (Ai>N) и (СК >N+M) : Проверка окончания одного из массивов
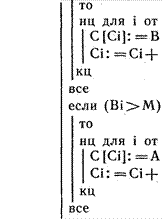 если (В>М) и (Ci< >N+M)
если (В>М) и (Ci< >N+M)кц
При решении данной задачи мы выполнили «слияние» двух отсортированных массива в один. Количество операций сравнения, которые понадобились для получения упорядоченного массива, равно N-FM.
На приведенном алгоритме основывается сортировка слияниями.
1. Разобьем все элементы массива на пары (группы) и упорядочим элементы в парах. Если последнему элементу нет пары, то он просто остается на своем месте, образуя отдельную группу.
2.
Выполним «слияние» соседних упорядоченных групп чисел, полученных на
предыдущем шаге (первой и второй, третьей и четвертой и т. д.; еслњ, количество
групп нечетное, то с последней группой ничего не делаем). Для «слияния»
придется воспользоваться вспомога![]() тельным массивом. Количество элементов во
всех группах, за исключением, может быть, последней, равно четырем.
тельным массивом. Количество элементов во
всех группах, за исключением, может быть, последней, равно четырем.
З. Выполним «слияние» соседних упорядоченных ![]() групп
чисел, полученных на предыдущем шаге. Получим упорядоченные группы элементов
массива, содержащие по восемь чисел, кроме, может быть, последней группы.
групп
чисел, полученных на предыдущем шаге. Получим упорядоченные группы элементов
массива, содержащие по восемь чисел, кроме, может быть, последней группы.
4. Продолжаем действовать таким образом до тех пор, пока не получим две отсортированные части массива, которые после слияния и дадут упорядоченный массив.
Алгоритм сортировки слияниями также имеет название алгоритма фон Неймана.
Алгоритм метода запишите самостоятельно.
Алгоритм сортировки слияниями требует порядка N log2 N операций сравнения и столько же перестановок элементов. Данный алгоритм является самым быстрым из всех рассмотренных выше алгоритмов сортировок (проверьте!).
Рассмотрим работу алгоритма на примере массива 1, 9, 2, 4, З, 6, 5, 0, 7, 11, 8. (Сортируем массив в порядке убывания.)

ЗАДАЧИ ДЛЯ ПОВТОРЕНИЯ
1. Дан линейный массив А [l..N], содержащий целые числа. Определить:
а) имеется ли в массиве хотя бы одно число с указанными ниже свойствами;
б) посчитать количество чисел, которые являются положительными;
2) являются нечетными;
З) отличны от А (К); К вводится;
4) делятся на З и на 5;
5) делятся на 7 и не делятся на 4;
6) при делении на З и на 5 дают одинаковые остатки;
7) при делении на 7 дают в остатке 1, 2 или З; 8) являются квадратом целого числа; 9) являются степенью 5.
![]() 2. Дан линейный массив А [1..N],
содержащий целые числа. Определить, сколько в нем соседств
2. Дан линейный массив А [1..N],
содержащий целые числа. Определить, сколько в нем соседств ![]()
1) двух положительных чисел;
2) двух разных чисел;
З) двух нечетных чисел;
4) двух нулевых элементов;
5) двух чисел одного знака, причем модуль первого должен быть больше модуля второго;
6) трех упорядоченных по неубыванию чисел.
З. Дан линейный массив А [l..N],
содержащий целые ![]() числа. Получить те элементы массива,
индексы которого являются
числа. Получить те элементы массива,
индексы которого являются
1) степенями двойки;
2) полными квадратами; З) числами Фибоначчи.
4. Дан линейный массив А [l..N], содержащий целые
числа.![]()
Г) Определить, сколько раз встречается максимальный элемент в этом массиве.
![]() 2) Получить те
элементы массива, которые находятся
2) Получить те
элементы массива, которые находятся ![]() ме>кду минимальным и максимальным.
ме>кду минимальным и максимальным.
З) Найти длину наименьшего отрезка числовой прямой, содержащего все элементы массива.
4) Найти минимальный, максимальный, наименьший больше минимального, наибольший меньше максимального за один просмотр массива.
5.
Дан линейный массив А [l..N], содержащий целые числа. Посчитать в нем![]()
![]() 1) наибольшее
количество одинаковых чисел; 2) количество различных чисел.
1) наибольшее
количество одинаковых чисел; 2) количество различных чисел.
6. При поступлении в институт лица, получившие двойку на первом экзамене, ко второму не допускаются. Считая фамилии абитуриентов и их оценки после первого экзамена исходными данными, составить список абитуриентов, допущенных ко второму экзамену.
7. Дан прямоугольный массив А [1..М, l..N]. Получить номер
1) столбца, содержащего максимальный элемент; 2) строки, содержащей минимальный элемент; З) столбца, сумма элементов которого максимальна; 4) строки, сумма элементов которой минимальна.
8. Дан прямоугольный массив А [l..M, l..N]. Получить номера
1) строк, в которых есть равные элементы;
2)
строк, суммы элементов в которых равны. ![]()
9. Дан прямоугольный массив А [1..М, l..N]. Получить линейный
массив В, в котором ![]()
l) B[i] — максимальный элемент Ј-й строки
массива А (i изменяется от 1 до М); 2) В [i] — минимальный элемент столбца
массива ![]() А (i изменяется от I до N).
А (i изменяется от I до N).
10. Дан линейный массив А [l..N], содержащий целые числа. Отсортировать его
[ ) методом «пузырька» в порядке возрастания;
2) методом «пузырька» в порядке возрастания модулей;
З) методом выбора, при помощи поиска минимального элемента в порядке возрастания;
4) методом выбора при помощи поиска
одновременно минимального и максимального элементов в порядке возрастания; ![]()
![]() 5) переставив все
нулевые элементы в конец массива; порядок ненулевых произвольный;
5) переставив все
нулевые элементы в конец массива; порядок ненулевых произвольный;
6) так, чтобы все четные элементы стояли в начале массива, а нечетные — в конце;
![]() 7) так, чтобы все
положительные элементы стояли в начале массива, отрицательные — в середине, а
нули — в конце;
7) так, чтобы все
положительные элементы стояли в начале массива, отрицательные — в середине, а
нули — в конце;
8) так, чтобы все положительные элементы стояли в начале массива, а отрицательные — в конце (относительный порядок следования элементов должен сохраниться);
9)
в порядке возрастания количества цифр в числах, входящих в массив
(сначала однозначные, затем двузначные и т. д.); порядок расположения чисел ![]() с
одинаковым количеством цифр должен сохраниться неизменным;
с
одинаковым количеством цифр должен сохраниться неизменным;
10) в порядке возрастания количества цифр в числах, входящих в массив (сначала однозначные, затем двузначные и т. д.); числа с одинаковым количеством цифр располагаются в порядке убывания.
11. Имеются весы без гирь и четыре различных груза. На каждую из двух чашек весов можно класть по одному грузу. Разложить грузы по убыванию массы, использовав пять взвешиваний.
12. Дан прямоугольный массив А [1..М, l..N]. Получить номера
1) строк, элементы которых расположены в возрастающем порядке;
2) столбцов, элементы которых расположены в убывающем порядке;
![]()
![]()
4) строк, элементы которых являются последовательными степенями двойки.
13. Фамилии участников
соревнований по фигурному катанию после короткой программы располо»кены в
порядке, соответствующем занятому месту. Составить список стартовых номеров
участников для произвольной ![]() программы (участники выступают в порядке,
обратном
программы (участники выступают в порядке,
обратном ![]() занятым местам).
занятым местам).
14. Дан отсортированный в порядке возрастания линейный массив А [1..N].
1) Определить, имеется ли в данном массиве число, равное среднему арифметическому элементов массива.
![]() 2) Вставить в данный
массив некоторое число Х так,
2) Вставить в данный
массив некоторое число Х так, ![]() чтобы упорядоченность массива сохранилась.
чтобы упорядоченность массива сохранилась.
![]() 15. Таблица выигрышей лотереи представлена
в виде двух массивов А [l..N] и C[l..Nl. В массиве А, упорядоченном по
убыванию, хранятся выигрышные номера, а в массиве С — выигрыши в рублях,
выпавшие соответственно на номера А [Ц, А [2] А [N]. Требуется найти выигрыши,
выпавшие на ряд номеров, хранящихся в массиве B[l..M] (если номера нет в
таблице, выигрыш считается равным нулю).
15. Таблица выигрышей лотереи представлена
в виде двух массивов А [l..N] и C[l..Nl. В массиве А, упорядоченном по
убыванию, хранятся выигрышные номера, а в массиве С — выигрыши в рублях,
выпавшие соответственно на номера А [Ц, А [2] А [N]. Требуется найти выигрыши,
выпавшие на ряд номеров, хранящихся в массиве B[l..M] (если номера нет в
таблице, выигрыш считается равным нулю). ![]()
16. Заданы
массивы А [1..N] и В [l..M]. Массив А упорядочен по убыванию. Подсчитать
количество тех В [i], 1 ![]() для которых нет равных среди элементов
массива А.
для которых нет равных среди элементов
массива А.
17. Задан массив А [l..N]. Получить в порядке возрастания все различные числа, входящие в массив А.
18. Лыжные гонки проводятся двумя группами по 10 человек. Результаты соревнований представлены списками участников по каждой группе, в порядке занятых ими мест. Необходимо получить общий список, в котором участники расположены в порядке, соответствующем показанным результатам.
19. ![]() Соревнования
по плаванию проводятся отдельно в Европе и Америке. Результаты 100 лучших
спортсме
Соревнования
по плаванию проводятся отдельно в Европе и Америке. Результаты 100 лучших
спортсме![]() нов каждого континента представлены в виде
таблиц, содержащих в порядке занятых мест фамилии спортсменов и их результаты.
Составить список 100 лучших спортсменов мира в порядке, определяемом
результатами.
нов каждого континента представлены в виде
таблиц, содержащих в порядке занятых мест фамилии спортсменов и их результаты.
Составить список 100 лучших спортсменов мира в порядке, определяемом
результатами.
20. В памяти ЭВМ хранится список фамилий абонентов в алфавитном порядке и номера их телефонов. Составить программу, обеспечивающую быстрый поиск абонента по номеру телефона.
21. В
памяти ЭВМ хранятся списки номеров телефо![]() нов и фамилий абонентов,
упорядоченные по номерам телефонов, для каждого из пяти телефонных узлов
города. Один телефонный узел включает несколько АТС (не более 10). Номера АТС
(первые две цифры номера телефона), относящиеся к каждому телефонному узлу,
также хранятся в упорядоченном виде в памяти ЭВМ. Составить программу,
обеспечивающую быстрый поиск фамилии абонента по заданному номеру телефона.
нов и фамилий абонентов,
упорядоченные по номерам телефонов, для каждого из пяти телефонных узлов
города. Один телефонный узел включает несколько АТС (не более 10). Номера АТС
(первые две цифры номера телефона), относящиеся к каждому телефонному узлу,
также хранятся в упорядоченном виде в памяти ЭВМ. Составить программу,
обеспечивающую быстрый поиск фамилии абонента по заданному номеру телефона.
22. Даны N монет, среди которых одна фальшивая. Определить фальшивую монету с помощью чашечных весов без гирь за минимальное количество взвешиваний, если фальшивая монета
1) тяжелее остальных;
![]() 2) легче остальных;
2) легче остальных;
З) отличается от остальных по массе и при этом не известно — тяжелее она или легче настоящей монеты.
23. Некто задумал число из промежутка [О, 100]. Он может правдиво отвечать «да» или «нет» на задаваемые ему вопросы. Какие вопросы нужно задавать, чтобы отгадать задуманное число за минимальное количество попыток.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ
1. Задан массив чисел А [1..N, 1..М], упорядоченный по возрастанию по строкам и по столбцам, так что
![]() А р, 1 КА [Е, [i, М] (при всех i),
А р, 1 КА [Е, [i, М] (при всех i),
А [1, [2, [N, ј] (при всех ј).
Найти индексы (i, ј) элемента массива, равного заданному числу Х, или напечатать слово «нет», если такого элемента не окажется.
2. Задан массив А [1..N, l..N], элементы которого равны 0 или 1, причем А [i, для любого i. Необходимо найти, если они есть, такие строку io и столбец јо, чтобы в столбце јо были все 0, а в строке все (кроме элемента А [Јо, Љ], равного 0).
З. На плоскости своими координатами задается выпуклыЙ ![]() Координаты
Координаты
![]() целочисленны
и перечисляются в порядке обхода по контуру. Вводятся координаты точки (х; у).
Определить
целочисленны
и перечисляются в порядке обхода по контуру. Вводятся координаты точки (х; у).
Определить
а) является ли она вершиной![]()
б)
принадлежит ли она![]()
4. На каждой из двух параллельных прямых слева направо заданы по N точек (рис. 28).
![]() Их координаты
хранятся в массивах A [l..N] и В В..М. Точки с одинаковыми номерами соединены
отрезками. Таким образом, полоса между прямыми разбивается на Рис. 28
Их координаты
хранятся в массивах A [l..N] и В В..М. Точки с одинаковыми номерами соединены
отрезками. Таким образом, полоса между прямыми разбивается на Рис. 28 ![]() конечную
и 2 бесконечные трапеции. Расстояние между прямыми единичное. Вводится точка
(х; у),
конечную
и 2 бесконечные трапеции. Расстояние между прямыми единичное. Вводится точка
(х; у), ![]() 1. Определить, в какой из трапеций лежит
точка.
1. Определить, в какой из трапеций лежит
точка.
5. Вводится
последовательность из N натуральных ![]() чисел. Определить наименьшее натуральное
число, отсутствующее в последовательности.
чисел. Определить наименьшее натуральное
число, отсутствующее в последовательности.
6. ![]() На
длинной перфоленте записаны N попарно различных положительных целых чисел. Ваша
ЭВМ может перематывать ленту на начало и считывать числа одно за другим.
Внутренняя память ЭВМ может хранить
На
длинной перфоленте записаны N попарно различных положительных целых чисел. Ваша
ЭВМ может перематывать ленту на начало и считывать числа одно за другим.
Внутренняя память ЭВМ может хранить ![]() только несколько целых чисел. Требуется
найти наименьшее положительное целое число, которого нет на ленте.
только несколько целых чисел. Требуется
найти наименьшее положительное целое число, которого нет на ленте. ![]() Опишите
алгоритм, который сделает это за небольшое количество перемоток ленты.
Опишите
алгоритм, который сделает это за небольшое количество перемоток ленты.
7. На
столе в двух столбиках лежат 64 золотые и 64 серебряные монеты соответственно.
Как серебряные, так и золотые монеты упорядочены по убыванию масс (самая
тяжелая — вверху, самая легкая — внизу). Массы всех монет разные. Какое
наименьшее количество взвешиваний необходимо для определения 64-й монеты в
порядке убывания масс среди всех 128 монет? (За один раз можно взвешивать две
монеты.)![]()
8. Задано N наборов монет из различных стран. Наборы упорядочены по невозрастанию массы монет. В i-M наборе а, монет. Определить за как можно меньшее число взвешиваний на чашечных весах К-ю по массе монету среди всех монет.
9. Заданы массивы А [1..N] и В [1..М]. Найти такие индексы и јо, что
где ![]()
10. Решить уравнение / на промежутке [а, Ь], на котором функция / (х) является монотонной и непрерывной. Корень найти с точностью п знаков после запятой.
11. В романе N глав. В главе ai страниц. Требуется издать роман в К томах так, чтобы объем самого толстого тома был минимален. Описать алгоритм, отвечающий на вопрос, каким будет объем V самого толстого тома. Делить и переставлять главы нельзя.
12. Имеется N камней
массой Al, 142, А м. Необхо![]() димо разбить их на две кучи таким образом,
чтобы массы куч отличались не более чем в 2 раза. Выдать сообщение, если этого
сделать нельзя.
димо разбить их на две кучи таким образом,
чтобы массы куч отличались не более чем в 2 раза. Выдать сообщение, если этого
сделать нельзя.
![]() 13. Условие задачи 12, только массы куч
отличаются не более чем в раза.
13. Условие задачи 12, только массы куч
отличаются не более чем в раза.
14. Даны две целочисленные таблицы А [1..10] и В [1..15]. Разработать алгоритм и написать программу, которая проверяет, являются ли эти таблицы похожими. (Две таблицы называются похожими, если совпадают множества чисел, встречающихся в этих таблицах.)
15. Задается словарь. Найти в нем все анаграммы (слова, составленные из одних и тех же букв).
16. На прямой окрасили N отрезков. Известны координата L [i] левого конца и координата R [i] правого конца отрезка для i 1, М. Найти сумму длин всех окрашенных частей прямой.
П р и м еч ан и е. Число N столь велико, что на выполнение Х 2 даже
простейших операций не хватит времени. ![]()
Модифи ка ция. На окружности окрасили N дуг. Известны угловая координата L [i] начала и R [i] конца Ј-й дуги (от начала к концу двигались, закрашивая дугу, против часовой стрелки). Какая доля окружности окрашена?
17. Имеется 2N чисел. Известно, что их можно разбить на пары таким образом, что произведение чисел в парах равны. Сделать разбиение, если числа: а) натуральные; б) целые.
![]() 18. Имеются числа 141, А2,
18. Имеются числа 141, А2, ![]()
Составить из них N пар (Ai, Вј) таким
образом, чтобы ![]() сумма произведений пар была максимальна
(минималь
сумма произведений пар была максимальна
(минималь![]() на). Каждое Ai и В] в парах встречаются
ровно по одному разу.
на). Каждое Ai и В] в парах встречаются
ровно по одному разу.
19. ![]() Упорядочить
по невозрастанию 5 чисел за 7 операций сравнения.
Упорядочить
по невозрастанию 5 чисел за 7 операций сравнения.
20. Пусть А — множество из N натуральных чисел. Ваша программа должна определить, существует ли по крайней мере одно подмножество В множества А, удовлетворяющее следующим условиям для любых Х, У, Z из
![]()
где У, Z} означает множество В без элементов Х, У и Z, SUM — сумма элементов соответствующего множества.
В случае положительного ответа программа должна найти подмножество В, удовлетворяющее условию ( * ) и состоящее из максимально возможного числа элементов.
![]() 21. Дано положительное целое число К и К
целых чисел Щ, к. Вычислить значение суммы S (M,
21. Дано положительное целое число К и К
целых чисел Щ, к. Вычислить значение суммы S (M,![]()
а) наибольшее;
б) наименьшее;
![]() в) наиболее близкое к нулю;
в) наиболее близкое к нулю;
![]()
г) наиболее близкое к заданному числу Р.
Пр им е ч а н и е. Число К столь велико, что числа А 1,
„42, . ![]() занимают примерно пятую часть памяти, отводимой для хранения данных, а на
выполнение k2 даже простейших операций не хватает времени.
занимают примерно пятую часть памяти, отводимой для хранения данных, а на
выполнение k2 даже простейших операций не хватает времени.
22. Даны
целые числа М и N и массив действительных чисел X[l..N]. Найти целое число i (1
![]() для
которого сумма
для
которого сумма ![]() + Х [i+M] ближе всего к нулю по модулю.
+ Х [i+M] ближе всего к нулю по модулю.
23. Дан массив Х [1 ..N]. Необходимо циклически сдвинуть его на К элементов влево (т. е. элемент Х [i] после сдвига должен стоять на месте Х [i— К]; тут мы считаем, что за Х [l] следует Х Разрешается использовать только несколько дополнительных переменных (дополнительного массива заводить нельзя!).
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Чему будут равны и х2, если: а) х, = Р (1. 0, 2. 0),
6) ![]() О, 4. ор
О, 4. ор![]()
Алг вещ Р(вещ а, Ь) нач вещ с

кон
2. Определить, можно ли представить заданное натуральное число в виде произведеЁия четырех последовательных натуральных чисел. Длина числа не более 250 символов. Конец числа — пробел.
![]() З. Написать программу, которая в двумерном массиве А
[1..N, 1..М] целых чисел, таком, что для всех 1 выполняется А [i, [i,
и выполняется А [i, [i+ 1, М], находит все элементы А [Е, Л, равные
j+i, или устанавливает, что таких элементов нет.
З. Написать программу, которая в двумерном массиве А
[1..N, 1..М] целых чисел, таком, что для всех 1 выполняется А [i, [i,
и выполняется А [i, [i+ 1, М], находит все элементы А [Е, Л, равные
j+i, или устанавливает, что таких элементов нет.
4.
![]() Написать программу, которая в двумерном массиве А [1..N, 1..М] целых
чисел, таком, что для всех 1 выполняется А [i, [i, j-F 1] и выполняется А [i,
МКА [i+ 1, М], находит все элементы А [i, Л, равные j+i, или устанавливает, что
таких элементов нет.
Написать программу, которая в двумерном массиве А [1..N, 1..М] целых
чисел, таком, что для всех 1 выполняется А [i, [i, j-F 1] и выполняется А [i,
МКА [i+ 1, М], находит все элементы А [i, Л, равные j+i, или устанавливает, что
таких элементов нет.
5. На прямой своими концами заданы N отрезков и точка Х. Определить, принадлежит ли точка межотрезочному интервалу. Если да, то указать концевые точки этого интервала. Если нет, то найти: а) какому количеству отрезков принадлежит точка; б) каким именно отрезкам принадлежит точка?
![]() 6. На прямой своими концами заданы N
отрезков. Найти точку, принадлежащую максимальному числу отрезков.
6. На прямой своими концами заданы N
отрезков. Найти точку, принадлежащую максимальному числу отрезков.
7.
8.
Дан прямоугольный треугольник АВС: LABC= —900 ; LBAC=a0 (00
![]() Катет ВС разделен на п равных частей:
Катет ВС разделен на п равных частей:![]()
![]() = lDlD21
= lDlD21![]()
Каждая из точек Д (1 ![]() 1) соединена отрезком
с вершиной А таким образом, что полученные отрезки разделяют угол ВАС на п
частей:
1) соединена отрезком
с вершиной А таким образом, что полученные отрезки разделяют угол ВАС на п
частей:
для введенных а (в градусах) и п определить
К (1 ![]() для которого значение выражения lak—a/nl
будет наименьшим.
для которого значение выражения lak—a/nl
будет наименьшим.
9. В треугольном королевстве, расположенном между ![]() тремя
пирамидами, где-то под пылью столетий спрятан вход в гробницу фараона
Тутрамзеса. Многие кладоискатели отправлялись в дорогу, чтобы найти вход в
гробницу и обнаружить несметные сокровища.
тремя
пирамидами, где-то под пылью столетий спрятан вход в гробницу фараона
Тутрамзеса. Многие кладоискатели отправлялись в дорогу, чтобы найти вход в
гробницу и обнаружить несметные сокровища.
Напрасно! Проклятие фараона гласило: как только кладоискатель попадает в треугольное королевство, он должен двигаться только прямолинейно в направлении к вершине одной из пирамид. При этом, преодолев половину пути, он должен некоторое время отдохнуть и затем снова отправиться в путь по направлению к какой-нибудь из трех пирамид. Каждый раз направление выбирается случайным образом. Существует ли в треугольном королевстве точка, в которую кладоискатель никогда не сможет попасть? Если да, то вход в гробницу останется навсегда скрытым и фараон навеки будет оставлен в покое.
![]() Написать программу для кладоискателя, показывающую на
экране только точки остановки путника. (Задаются координаты трех угловых точек
треугольного королевства и начальное положение кладоискателя.)
Написать программу для кладоискателя, показывающую на
экране только точки остановки путника. (Задаются координаты трех угловых точек
треугольного королевства и начальное положение кладоискателя.)
Получить как минимум 5 графиков. Один из них ![]() должен
быть для следующих начальных условий: начальная точка и три вершины лежат в 4
углах экрана; проделать 5000 итераций.
должен
быть для следующих начальных условий: начальная точка и три вершины лежат в 4
углах экрана; проделать 5000 итераций.
![]() 10. Предположим, что имеется некоторый
кусок ленты, разделенный на кадры. Кадры занумерованы с двух сторон. Полоска
ленты склеена в лист Мебиуса. Необходимо составить алгоритм упорядочения этой
последовательности, предположив, что соседние кадры можно переставлять
(естественно, в упорядоченной поспледовательности будет один «скачок» от
минимального элемента к максимальному). Следует учесть, что при перестановке
кадров переставляются числа с обеих сторон кадров.
10. Предположим, что имеется некоторый
кусок ленты, разделенный на кадры. Кадры занумерованы с двух сторон. Полоска
ленты склеена в лист Мебиуса. Необходимо составить алгоритм упорядочения этой
последовательности, предположив, что соседние кадры можно переставлять
(естественно, в упорядоченной поспледовательности будет один «скачок» от
минимального элемента к максимальному). Следует учесть, что при перестановке
кадров переставляются числа с обеих сторон кадров.
Например: есть 2 кадра, Д, В] — одна сторона кадров, А2, В2 —
другая. Пусть 4=2, В; —7, Щ = З. Тогда после перестановки содержимого А и В
будет Al — ![]() 7, АБЗ, Вј=1, Щ=2.
7, АБЗ, Вј=1, Щ=2. ![]()
Всегда ли такое упорядочение возможно?
11. Имеется
N человек и целые числа А 1, ![]() Может ли число знакомых человека в этой
группе равняться АР
Может ли число знакомых человека в этой
группе равняться АР
12. Условие задачи l l. Указать один из возможных вариантов знакомств.
13. Задано семейство множеств букв. Найти такое максимальное К, для которого можно построить множество, состоящее из К букв, причем каждая из них принадлежит ровно К множествам заданного семейства.
14. В музее регистрируется в течение дня время прихода и ухода каждого посетителя. Таким образом за день получены N пар значений, где первое значение в паре показывает время прихода посетителя, а второе значение — время его ухода. Найти промежуток времени, в течение которого в музее одновременно находилось максимальное число посетителей.
15. ![]()
![]()
![]() Задается
число 1, которое определяет размерность пространства и размеры М п-мерных
параллелепипедов (ал, ...,
Задается
число 1, которое определяет размерность пространства и размеры М п-мерных
параллелепипедов (ал, ..., ![]() 1, М. Параллелепипед может располагаться в
пространстве любым из способов, при
1, М. Параллелепипед может располагаться в
пространстве любым из способов, при ![]() которых его ребра параллельны осям
координат. Найти максимальную последовательность вкладываемых друг в друга
параллелепипедов.
которых его ребра параллельны осям
координат. Найти максимальную последовательность вкладываемых друг в друга
параллелепипедов.
16. Построить
максимальное множество, состоящее из попарно не сравнимых векторов о. Векторы v
определяются парами чисел, выбираемых из данной после- ![]() довательности чисел щ,
ап, п Два вектора
довательности чисел щ,
ап, п Два вектора ![]() Ь) и
Ь) и ![]() называются сравнимыми,
если а<а' и b<b' или а>а' и b>b', в противном случае —
несравнимыми.
называются сравнимыми,
если а<а' и b<b' или а>а' и b>b', в противном случае —
несравнимыми.
17. Пусть группа состоит из N человек. Назовем одного из этих людей знаменитостью, если он не знает никого из оставшихся, а его знают все. Задача состоит в том, чтобы в этой группе определить знаменитость (если она там есть). При этом разрешается задавать только вопросы вида: «Извините, знаете ли Вы вон того человека?» (Предполагается, что все ответы правдивы,
4 Информатика, 8—9 кл.
и что даже знаменитость ответит на поставленный ей вопрос.)
Найти минимальное необходимое число вопросов, которые надо задать, и описать алгоритм опроса.
Входные данные: матрица С [i, ј], такая, что С [i, ![]() =
1, если i знает ј, и C[i, если иначе.
=
1, если i знает ј, и C[i, если иначе.
18.
На бирже есть N продавцов и М покупателей ![]() и один вид товара.
Каждый продавец определяет для себя и объявляет минимальную цену, по которой он
согласен продать товар, а каждый покупатель называет максимальную цену, по
которой он еще согласен купить товар.
и один вид товара.
Каждый продавец определяет для себя и объявляет минимальную цену, по которой он
согласен продать товар, а каждый покупатель называет максимальную цену, по
которой он еще согласен купить товар.
Найти такую единую цену на товар, чтобы сумма ![]() сделок
купли-продажи была максимальной.
сделок
купли-продажи была максимальной.
Найти такую максимальную единую цену на товар, чтобы общее количество продавцов и покупателей, участвующих в торгах, было максимальным.
19.
Пусть blackbox(u) — функция аргумента![]()
![]()
![]() 1, если
слово является частью неизвестного слова ш, и О—в противном случае.
1, если
слово является частью неизвестного слова ш, и О—в противном случае.
Разработать программу нахождения слова ш с помощью как можно более короткой последовательности вызовов функции blackbox.
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ
ПОВЫШЕННОЙ СЛОЖНОСТИ
1. Для решения задачи необходимо
сравнить число Х с элементами массива. Если сравнивать Х со всеми элементами
массива А, количество операций сравнения ![]() равно M•N.
равно M•N.
Существенно сократить количество сравнений можно, если
рассматривать первую строку и последний столбец массива А как один массив.
Элементы в нем упорядочены по возрастанию.![]()
Рассмотрим элемент А [1, М].![]()
Возможны следующие ситуации.
![]()
![]() В этом случае заданный элемент найден.
В этом случае заданный элемент найден.![]()
![]()
Тогда элемента, равного Х, в столбце с номером М ![]() быть
не может. Поэтому можно ограничиться поиском заданного элемента в массиве А с
выброшенным М-м столбцом.
быть
не может. Поэтому можно ограничиться поиском заданного элемента в массиве А с
выброшенным М-м столбцом.
В этом случае элемента, равного Х, в строке с номером быть не может. Поэтому в дальнейшем поиск заданного элемента будет проводиться в массиве А без первой строки.
Таким образом, на каждом шаге, после сравнения заданного элемента Х со значением элемента из правого верхнего угла массива, из массива выбрасывается либо строка, либо столбец. В результате этого суммарное число строк и столбцов уменьшается на 1. Поэтому для решения задачи потребуется не более чем N-FM сравнений.
![]() 2. Номера строки и столбца јо должны
совпадать, иначе в строке будет недиагональный нулевой элемент. Простейшим
решением является просмотр элементов
2. Номера строки и столбца јо должны
совпадать, иначе в строке будет недиагональный нулевой элемент. Простейшим
решением является просмотр элементов ![]() строки и ј-го столбца,
строки и ј-го столбца, ![]() N, массива
до нахождения индекса К такого, что элементы К-й строки и К-го столбца
удовлетворяют требуемому свойству или до установления факта, что такого индекса
нет. Очевидно, что в последнем случае необходим просмотр почти всех элементов
массива.
N, массива
до нахождения индекса К такого, что элементы К-й строки и К-го столбца
удовлетворяют требуемому свойству или до установления факта, что такого индекса
нет. Очевидно, что в последнем случае необходим просмотр почти всех элементов
массива.
Однако возможно существенно сократить количество операций, используя следующий факт.
Рассмотрим элемент А
[К, Л, Возможны две ![]() ситуации:
ситуации:
![]()
В этом случае можно заметить, что индекс К не подходит, так
как в строке с индексом К стоит 0. Поэтому можно ограничиться поиском заданного
элемента в подмассиве без К-го столбца и К-й строки. ![]()
![]() 1.
1.
![]()
В этом случае можно заметить, что индекс не подходит, так как в столбце с индексом ј стоит 1. Поэтому можно ограничиться поиском заданного элемента в подмассиве без ј-го столбца и /-й строки.
Таким образом, рассматривая на каждом шаге значения элементов А [К, Л таких, что А [К, ј] является элементом интересующего нас подмассива, потребуется просмотр ровно М— элемента для установления единственного индекса К, который может удовлетворить требуемому свойству. Остается проверить только элементы этого столбца и строки.
К: —1 для ј от 2 до N если А [К, ![]() то
к:
то
к:![]()
![]() После окончания цикла остается проверить только элементы
К-го столбца и К-й строки.
После окончания цикла остается проверить только элементы
К-го столбца и К-й строки. ![]()
![]() Суммарная трудоемкость описанного алгоритма не превосходит
3N операций.
Суммарная трудоемкость описанного алгоритма не превосходит
3N операций.
З. Простейшим решением является просмотр координат вершин ![]() и
определение, совпадают ли координаты одной из них с координатами точки (х; у).
В этом случае необходим просмотр координат всех N вершин многоугольника.
и
определение, совпадают ли координаты одной из них с координатами точки (х; у).
В этом случае необходим просмотр координат всех N вершин многоугольника.
Сократить количество операций просмотра можно, используя метод дихотомии.
Пронумеруем вершины от I до N в порядке обхода по ![]() контуру
и занесем координаты вершин в массив.
контуру
и занесем координаты вершин в массив.
Сравним вначале координату первой вершины в обходе с координатами точки (х; у). Если они совпадают, то задача решена. Если не совпадают, то точка (х, у) может совпадать с одной из оставшихся N— 1 вершиной. Номер начальной вершины оставшегося участка контура равен 2, конечной — N.
Пусть на некотором шаге номера начальной и конечной вершин
рассматриваемого контура равны и q соответственно. Найдем номер средней вершины
т— ![]() div 2. Определим теперь положение точки
(х; у) и вершины с номером относительно прямой, проходящей через вершины с
номерами 1 и т. Возможны следующие ситуации:
div 2. Определим теперь положение точки
(х; у) и вершины с номером относительно прямой, проходящей через вершины с
номерами 1 и т. Возможны следующие ситуации:
1)
Точки лежат по одну сторону от прямой. В этом ![]() случае нас не
интересует часть контура от вершины т до вершины q. Поэтому последней
интересующей нас вершиной в контуре можно считать вершину rn— l. Полагаем q: =
т— 1.
случае нас не
интересует часть контура от вершины т до вершины q. Поэтому последней
интересующей нас вершиной в контуре можно считать вершину rn— l. Полагаем q: =
т— 1.
2) Точки лежат по разные стороны от прямой. В этом случае нас не интересует часть контура от вершины до вершины т— 1. Поэтому первой интересующей нас вершиной в контуре можно считать вершину т. Полагаем р. = т.
Процесс заканчивается, когда q—f— I (т. е. осталось только две точки). Проверка их координат на совпадение с точкой (х; у) и дает ответ на поставленный в задаче вопрос.
Пр и м е ч а н и е. Для решения задачи нам понадобилось проанализировать О N) вершин.
Этот пример показывает, что метод дихотомии можно применять не только к числовым упорядоченным множествам.
4. Пронумеруем трапеции слева направо
от 1 до N+ 1. Левая бесконечная трапеция имеет номер 1, пра![]() вая — (N-F
1), конечные трапеции от 2 до N.
вая — (N-F
1), конечные трапеции от 2 до N.
Простейшим решением является
последовательное определение положения точки (х; у) относительно прямых,
проходящих через точки с координатами (Д 1), ![]() (Bi_l; 0) и (Ах, 1),
(ВГ, 0) соответственно, i=2, . . . , N. Возможны следующие ситуации.
(Bi_l; 0) и (Ах, 1),
(ВГ, 0) соответственно, i=2, . . . , N. Возможны следующие ситуации.![]()
![]()
![]() 1) Точка лежит по одну сторону от прямых.
1) Точка лежит по одну сторону от прямых.
![]() Полагаем i: =i+l.
Полагаем i: =i+l.
2) Точка лежит по разные стороны от прямых. Тогда интересующей нас трапецией является конечная грапеция с индексом i.
![]() Если мы проанализировали все конечные
трапеции, а ситуация 2) не возникла, то точка лежит в одной из бесконечных
трапеций. Проверим, лежат ли точка (х; у) и точка из левой бесконечной трапеции
по одну сторону от прямой, проходящей через точки (А 1', 1), (Щ; О). Если да,
то точка принадлежит левой бесконечной трапеции, если нет — правой.
Если мы проанализировали все конечные
трапеции, а ситуация 2) не возникла, то точка лежит в одной из бесконечных
трапеций. Проверим, лежат ли точка (х; у) и точка из левой бесконечной трапеции
по одну сторону от прямой, проходящей через точки (А 1', 1), (Щ; О). Если да,
то точка принадлежит левой бесконечной трапеции, если нет — правой.
Однако можно существенно сократить количество операций, используя метод дихотомии.
![]() Определим индексы начального и конечного
номеров интересующих нас трапеций, среди которых будет искомая. Вначале индексы
равны и N+l соответственно.
Определим индексы начального и конечного
номеров интересующих нас трапеций, среди которых будет искомая. Вначале индексы
равны и N+l соответственно.
![]() Пусть на некотором
шаге индексы начального и конечного номеров интересующих нас трапеции равны
Пусть на некотором
шаге индексы начального и конечного номеров интересующих нас трапеции равны ![]() и q
соответственно. Вычислим индекс среднего номера
и q
соответственно. Вычислим индекс среднего номера ![]() div 2.
div 2.
![]()
![]() Определим
взаимное расположение точки (х; у) и точки, лежащей заведомо в левой
бесконечной трапеции, относительно прямой, проходящей через точки с
координатами (А т; 1), (Вт; О).
Определим
взаимное расположение точки (х; у) и точки, лежащей заведомо в левой
бесконечной трапеции, относительно прямой, проходящей через точки с
координатами (А т; 1), (Вт; О).
Возможны следующие ситуации.
![]() 1) Точки лежат по одну сторону от прямой.
В этом
1) Точки лежат по одну сторону от прямой.
В этом ![]() случае нас не интересуют трапеции с
номерами от т до q.
случае нас не интересуют трапеции с
номерами от т до q.
Полагаем q: = т.
2) Точки лежат по разные стороны от
прямой. В этом случае нас не интересуют трапеции с номерами от ![]() до т.
Полагаем р.
до т.
Полагаем р.![]()
![]() Алгоритм заканчивает работу, когда /—q.
Искомая
Алгоритм заканчивает работу, когда /—q.
Искомая ![]() трапеция имеет номер г.
трапеция имеет номер г.
5.
Среди N введенных натуральных чисел отсутствует по крайней мере
одно число из интервала [1, N-F l]. Идея решения состоит в использовании
массива из N чисел, в котором элемент с индексом i «регистрирует», пришло ![]() ли
число со значением Г. После «регистрации» всех элементов последовательности
остается только проверить, какое минимальное число не «зарегистрировано».
ли
число со значением Г. После «регистрации» всех элементов последовательности
остается только проверить, какое минимальное число не «зарегистрировано».
В качестве признака «регистрации» числа i можно заносить в элемент массива l. Первоначально все числа «незарегистрированы» — все элементы массива равны 0.
Если все числа от до N «зарегистрированы», то минимальное отсутствующее натуральное — N+ 1.
6. Очевидно, что при вводе N натуральных чисел по крайней мере одно число из интервала [1, АУ -6- Ц отсутствует.
![]() Определим начало а и конец Ь некоторого
интервала индексов, который нас интересует. Возможно ли за один просмотр ленты
установить, все ли числа из интервала [а, Ь] присутствуют на ленте? Учитывая
тот факт, что записанные числа различны, можно определить, сколько чисел,
записанных на ленте, попадают в интересующий нас интервал. С другой стороны,
нетрудно определить
Определим начало а и конец Ь некоторого
интервала индексов, который нас интересует. Возможно ли за один просмотр ленты
установить, все ли числа из интервала [а, Ь] присутствуют на ленте? Учитывая
тот факт, что записанные числа различны, можно определить, сколько чисел,
записанных на ленте, попадают в интересующий нас интервал. С другой стороны,
нетрудно определить
![]()
количество натуральных чисел на интервале [а, Ь] — это
Алгоритм состоит в следующем.![]()
Определим значения начала и конца интересующего нас
интервала. Очевидно, что вначале они равны ![]() и N+l соответственно.
и N+l соответственно.
Пусть на некотором шаге значения начала и конца интересующего
нас интервала равны и q соответственно. Определим индекс среднего элемента
интервала т. = ![]() (/+q) div 2.
(/+q) div 2.
Найдем теперь количество элементов К на ленте, лежащих в интервале т]. Возможны следующие ситуации.
l) Количество элементов ![]() В этом
случае
В этом
случае ![]() нас не интересует интервал от т до q, так
как на интервале [Р, т] хотя бы одно число отсутствует.
нас не интересует интервал от т до q, так
как на интервале [Р, т] хотя бы одно число отсутствует. ![]() Поэтому интересующим
нас интервалом можно
Поэтому интересующим
нас интервалом можно ![]() считать [Т, т]. Поэтому полагаем q: = т.
считать [Т, т]. Поэтому полагаем q: = т. ![]()
2) Количество элементов 1. В этом случае ![]() нас не
интересует интервал от до т, так как на
нас не
интересует интервал от до т, так как на ![]() интервале [Р, т]
все натуральные числа присутст
интервале [Р, т]
все натуральные числа присутст![]() вуют. Таким образом, интересующим нас
интерва
вуют. Таким образом, интересующим нас
интерва![]()
JIOM
MO>KHO C t4HTaTb [m*- 1, q]. 1103TOMY fl0J1araeM![]()
![]()
Ilpouecc OKaHMHBaeTCfl, Korma /=q. 3HaqeHue fiBJ1%eTCH HCKOMb1M.
7. C03maÅMM ABa MaCCHBa, ![]() H3 KOTOPb]X 6ymeT cmepxaTb MaCCb1
MOHeT H3 nepBoro H BToporo CTOJ16HKOB COOTBeTCTBeHHO.
H3 KOTOPb]X 6ymeT cmepxaTb MaCCb1
MOHeT H3 nepBoro H BToporo CTOJ16HKOB COOTBeTCTBeHHO.
OqeBHAHoe pemeHue 3amaHH — ![]() 9THX
9THX ![]() MaCCHBOB B 06111Hü ynopqmoqeHHb1i
MaCCHB BeCOB H HaXO>KmeHue B HeM 64-ro no BeJIH LIHHe 3J1eMeHTa.
MaCCHBOB B 06111Hü ynopqmoqeHHb1i
MaCCHB BeCOB H HaXO>KmeHue B HeM 64-ro no BeJIH LIHHe 3J1eMeHTa.
OÅHaKO aamaqy MO>KHO pelliHTb 6b1cTpee, HCflOJ1b3Yfl MeTOÅ AHXOTOMHH. I-IPH 3TOM He B03HHKaeT He06XOÅHMOCTU 06%eÅHHHTb HCXOAHb1e MaCCHBbr.
0603HaqHM COOTBeTCTBeHHO qepe3 Ni H Ki HaqaJ1bHb1i H KOHeHHb1Ü
H0Mepa 9.neMeHTOB B paccMaTpHBaeMb1x Ha maHHOM mare MaccHBax, l, 2. OnpemeJIHM
H0Mepa cpemHHX 3J1eMeHTOB div 2. Ha nepB0M mare N i = l, K] —64, N2=1, 16=64,
$=32,![]()
![]() MeHTOB, CTOHUIHX Ha MecTe Si, 1, 2,
0603HaqHM X H Y.
MeHTOB, CTOHUIHX Ha MecTe Si, 1, 2,
0603HaqHM X H Y. ![]() CpaBHHB cpeAHHe 3J1eMeHTb1 X H Y, HaimeM 60J1bUIHä H3 HHX. flycTb X.
B CHJIY ynopqmoqeHHocTH MaccHBa Ka>KÅb1ü H3 3J1eMeHTOB, CTOHUIUX
nepeA X, 60J1bU.1e X no BeJIHqH1--re. C Apyroü CTOPOHb1, TOJ1bKO
3,neMeHTb1, CT0fl11iue nepeA Y BO BTOPOM MaCCHBe, MOPYT 6b1Tb 60J1b1.Ue X.
1103TOMY X 60J1bU-1e HCKOMOPO 64-ro 9JJewreHTa. CJ1eAOBaTeJ1bHO, B nepBOM MaCCHBe
MO>KHO He paCCMaTPHBaTb nepBb1e 32 3,neMe1-1Ta.
CpaBHHB cpeAHHe 3J1eMeHTb1 X H Y, HaimeM 60J1bUIHä H3 HHX. flycTb X.
B CHJIY ynopqmoqeHHocTH MaccHBa Ka>KÅb1ü H3 3J1eMeHTOB, CTOHUIUX
nepeA X, 60J1bU.1e X no BeJIHqH1--re. C Apyroü CTOPOHb1, TOJ1bKO
3,neMeHTb1, CT0fl11iue nepeA Y BO BTOPOM MaCCHBe, MOPYT 6b1Tb 60J1b1.Ue X.
1103TOMY X 60J1bU-1e HCKOMOPO 64-ro 9JJewreHTa. CJ1eAOBaTeJ1bHO, B nepBOM MaCCHBe
MO>KHO He paCCMaTPHBaTb nepBb1e 32 3,neMe1-1Ta.
![]() AHaJ10rH t-1HO MO>KHO
110Ka3aTb, YTO 3J1eMeHTb1, CTOHLÅHe nocjre Y, MOXHQ •raK>Ke He
paccMaTPHBaTb, Tax KaK OHM MeHb111e HCKOMTO 3J1eMeHTa. 110CJ1e TaKHX
meÜCTBHi B MacCHBax OCTaJIOCb no 32 3J1eMeHTa, H STOM He06XOÅHMO
HaiTH 32-ü no BeJIH4HHe 3J1eMeHT.
AHaJ10rH t-1HO MO>KHO
110Ka3aTb, YTO 3J1eMeHTb1, CTOHLÅHe nocjre Y, MOXHQ •raK>Ke He
paccMaTPHBaTb, Tax KaK OHM MeHb111e HCKOMTO 3J1eMeHTa. 110CJ1e TaKHX
meÜCTBHi B MacCHBax OCTaJIOCb no 32 3J1eMeHTa, H STOM He06XOÅHMO
HaiTH 32-ü no BeJIH4HHe 3J1eMeHT.
![]()
3HaqeHHflMM HaqaJ1bHb1X Ni, KOHeMHb1X Ki H cpeAHHX Si
HOMepoB 3,RMeHTOB B MaCCHBax no ceneAyrouxeMY npaBHJ1y: ecJIH 60J1b111Hi H3 X H
Y HaXOÅflTCH B nepB0M MaccHBe, TO NI=Si+1, K2=S2, HHaqe N2=S2+l, KI=SI.![]()
заканчивается, когда в каждом массиве останется по одному элементу. При этом больший из них и будет искомым.
П р и м е ч а н и е. Поскольку количество монет после каждого шага уменьшается в два раза, то количество взвешиваний — log2128=7.
8. Очевидным решением задачи является создание общего упорядоченного массива, содержащего элементы всех исходных массивов, и нахождение в нем К-го по величине элемента.
П р и ме ч а н и е. В этом случае требуется порядка (щ +аН-... + + ал) log2 (Щ + ад) операций.
Однако можно существенно сократить количество операций, используя дихотомический способ поиска.
ДЛЯ массивов с kj<Nj ПО
правилу Sj=kj. На каждой итерации вычисляем значение![]()
![]()
Возможны три ситуации.
![]()
В этом случае искомый элемент не меньше
минимального среднего элемента min (пусть он находится в наборе с номером ј).
Тогда элементы с индексами Si, К/ заведомо не являются ![]() решением и их можно
игнорировать. Поэтому пересчитываем К] по правилу
решением и их можно
игнорировать. Поэтому пересчитываем К] по правилу ![]() (напомним, что
kj>Ni).
(напомним, что
kj>Ni).
![]()
В этом случае искомый элемент не больше
макси![]() мального элемента тах (пусть он находится
в наборе с номером t). Тогда элементы с индексами
мального элемента тах (пусть он находится
в наборе с номером t). Тогда элементы с индексами
![]() St заведомо не являются решением и их
можно игнорировать. Поэтому пересчитываем
St заведомо не являются решением и их
можно игнорировать. Поэтому пересчитываем ![]() по правилу Nt—St+l
(напомним, что kt>Nt).
по правилу Nt—St+l
(напомним, что kt>Nt).
![]()
В этом случае можно пересчитать kj=S. и![]()
![]()
Процесс заканчивается, когда начальный Ni и конечный Кг индексы удовлетворяют условию ki<Ni для каждого г. При этом меньший из элементов с индексами ki и будет искомым (если то этот элемент рассматривать не нужно).
![]() 9. Для решения задачи достаточно
осуществлять просмотр элементов массивов А и В, фиксируя две величины:
9. Для решения задачи достаточно
осуществлять просмотр элементов массивов А и В, фиксируя две величины:
1) положение р максимального
просмотренного эле![]() мента из А;
мента из А;
![]() 2) значение индексов io, јо для
максимальной найденной суммы, удовлетворяющей требованию условия. На начальном
этапе p=l,
2) значение индексов io, јо для
максимальной найденной суммы, удовлетворяющей требованию условия. На начальном
этапе p=l, ![]() 2.
2.
При просмотре очередного элемента i из А определяется:
максимальная из сумм
![]()
пересчетом индексов io, јо для
максимальной найденной суммы; индекс р максимального просмотренного элемента ![]() из А
(при сравнении значений А [р] и А [i]).
из А
(при сравнении значений А [р] и А [i]).
Действия выполняются для i от 2 до т— 1,
![]() 10. Если функция является монотонной и
непрерывной на промежутке [а, Ь] и имеет на концах промежутка значения разных
знаков, то она имеет на этом промежутке единственный корень, который можно
найти методом дихотомии.
10. Если функция является монотонной и
непрерывной на промежутке [а, Ь] и имеет на концах промежутка значения разных
знаков, то она имеет на этом промежутке единственный корень, который можно
найти методом дихотомии.
Если функция имеет на промежутке единственный корень, то
значения функции на концах этого промежутка имеют разные знаки, т.е. ; (а) ![]() Найдем
середину отрезка [а,
Найдем
середину отрезка [а, ![]() Ь)/2. Точка с разделит наш промежуток на
две части. Вычислим значение / (с). Если р (с то с — корень уравнения. Если Нс
то либо либо
Ь)/2. Точка с разделит наш промежуток на
две части. Вычислим значение / (с). Если р (с то с — корень уравнения. Если Нс
то либо либо ![]() В качестве нового промежутка [а, Ь] берем
тот, на концах которого функция
В качестве нового промежутка [а, Ь] берем
тот, на концах которого функция ![]() принимает значения разных знаков. Длина
промежутка сократилась вдвое. Разделим [а, Ь] пополам и из двух полученных
промежутков выберем тот, на концах которого функция принимает значения разных
знаков, и т. д.
принимает значения разных знаков. Длина
промежутка сократилась вдвое. Разделим [а, Ь] пополам и из двух полученных
промежутков выберем тот, на концах которого функция принимает значения разных
знаков, и т. д.
Процесс продолжается до тех пор, пока модуль значения функции
в найденной на данном шаге точке х не будет меньше 10 ¯n (если п— 5, то
(x)l![]()
11. Попытаемся распределить главы по томам равномерно. На
каждый том придется не более Р== rN/IO глав, где ГЛ округление по избытку. Тома
с 1-го по (К— 1)-й будут содержать по Р глав, а том с номером ![]() РК) глав.
Найдем максимальный объем тома при таком распределении. Запомним его в
переменной high. Это будет оценка минимального объема V сверху.
РК) глав.
Найдем максимальный объем тома при таком распределении. Запомним его в
переменной high. Это будет оценка минимального объема V сверху.
![]() div 2.
div 2.
Попытаемся распределить главы по томам так, чтобы объем каждого тома не превосходил level. Будем заносить в очередной том главы до тех пор, пока добавление следующей главы не приведет к превышению level. После этого перейдем к формированию следующего тома.
Если нам удалось распределить все главы по томам, то мы нашли новую оценку для V сверху. В этом случае полагаем high=level.
Если же мы сформировали последний том и после этого осталась еще хотя бы одна глава, то с максимальным объемом тома не более level главы распределить нельзя. Требуется увеличить нижнюю оценку. Полагаем [ош : = level+ 1.
![]() Повторяем этот процесс до тех пор, пока не
станет [ош >high (тем самым объем искомого тома V уточнен до одной
страницы). Значение high и будет искомым минимальным объемом самого толстого
тома.
Повторяем этот процесс до тех пор, пока не
станет [ош >high (тем самым объем искомого тома V уточнен до одной
страницы). Значение high и будет искомым минимальным объемом самого толстого
тома.
Применение метода дихотомии к решению данной задачи позволяет значительно сократить перебор возможных вариантов.
![]() 12. Основная стратегия решения заключается
в том, что каждый следующий камень кладется в кучу с меньшей текущей массой.
При этом в первую кучу надо положить камень максимальной массы. Покажем, что
этого достаточно, чтобы гарантировать правильное решение задачи. По окончании
распределения камней по кучам возможны 2 ситуации:
12. Основная стратегия решения заключается
в том, что каждый следующий камень кладется в кучу с меньшей текущей массой.
При этом в первую кучу надо положить камень максимальной массы. Покажем, что
этого достаточно, чтобы гарантировать правильное решение задачи. По окончании
распределения камней по кучам возможны 2 ситуации:
1) Все камни попали во вторую кучу, а ее
масса ![]() осталась меньше половины массы первой
кучи. Понятно, что в этом случае камни требуемым образом разбить нельзя,
следовательно, решения не существует.
осталась меньше половины массы первой
кучи. Понятно, что в этом случае камни требуемым образом разбить нельзя,
следовательно, решения не существует.
![]() 2) Случай не выполняется. Тогда возможны
следующие ситуации.
2) Случай не выполняется. Тогда возможны
следующие ситуации.
а) Все камни попали во вторую кучу. В
этом случае ![]() ясно, что массы куч отличаются не более
чем на половину первой кучи, если масса первой кучи больше, или не более чем на
массу последнего камня, положенного во вторую кучу. „В любом из этих случаев
требуемое условие выполняется.
ясно, что массы куч отличаются не более
чем на половину первой кучи, если масса первой кучи больше, или не более чем на
массу последнего камня, положенного во вторую кучу. „В любом из этих случаев
требуемое условие выполняется.
![]() б) В первую кучу
попали и другие камни. Тогда ясно, что массы куч отличаются не более чем на
массу
б) В первую кучу
попали и другие камни. Тогда ясно, что массы куч отличаются не более чем на
массу ![]() самого тяжелого камня, кроме первого. Следова
самого тяжелого камня, кроме первого. Следова![]() тельно, и в этом случае условие задачи выполняется.
тельно, и в этом случае условие задачи выполняется.
![]() 13. На начальном этапе в первую кучу
кладется самый тяжелый камень, а во вторую — два следующих
13. На начальном этапе в первую кучу
кладется самый тяжелый камень, а во вторую — два следующих
по массе камня. Для оставшихся камней реализуется описанная для задачи 12 стратегия.
14. Мы можем отсортировать оба массива — и А, и В (например, по неубыванию), далее, если первые элементы массивов А и В совпадают, то ищем и в А, и в В минимальные элементы больше данного и повторяем сравнения; если же элементы не совпадают либо один из массивов уже закончился, а другой еще нет, то массивы не похожи.
{А и В уже отсортированы} i : = 1; {смотрим массивы А и В,
начиная с первых} Ј: — 1; {элементов} while = 10) and ![]() do
begin element: ==А [il; while = 10) and
do
begin element: ==А [il; while = 10) and ![]() do i :
do i : ![]() 1; {поиск
несовпадающего элемента} while
1; {поиск
несовпадающего элемента} while ![]() = 15) and (В [jl=element) do ј : =j-F 1;
{поиск несовпадающего элемента) end;
= 15) and (В [jl=element) do ј : =j-F 1;
{поиск несовпадающего элемента) end; ![]() if (i 11) and (ј• = 16)
{просмотрели все элементы
if (i 11) and (ј• = 16)
{просмотрели все элементы
then writeln ('Массивы похожи ![]() else writeln ('Массивы непохожи');
else writeln ('Массивы непохожи');
15. Каждому слову приписываем номер в словаре. Сначала сортируем буквы в каждом слове по (например) неубыванию. Получаем какой-то «ключ», который совпадает у всех слов-анаграмм (например, слова «лом» и «мол» преобразуются в одни и те же ключи «лмо»).
Далее мы сортируем ключи слов (совместно с приписанными
номерами) по неубыванию. Все одинаковые ключи будут размещаться в
отсортированной последовательности слов друг за другом. Мы просматриваем полу![]() ченную
последовательность, ищем совпадающие ключи и по приписанным им номерам находим
в словаре соответствующие слова-анаграммы.
ченную
последовательность, ищем совпадающие ключи и по приписанным им номерам находим
в словаре соответствующие слова-анаграммы.
![]() 16. Отсортируем отрезки в порядке
неубывания коор
16. Отсортируем отрезки в порядке
неубывания коор![]() динат левых концов и будем моделировать
последовательное их закрашивание, начиная с самого левого отрезка. Назовем
закрашиваемым тот отрезок, который
динат левых концов и будем моделировать
последовательное их закрашивание, начиная с самого левого отрезка. Назовем
закрашиваемым тот отрезок, который ![]() является объединением одного или
нескольких отрезков. Каждый раз, когда берем новый отрезок из упорядоченной
последовательности, мы анализируем следующие возможные ситуации.
является объединением одного или
нескольких отрезков. Каждый раз, когда берем новый отрезок из упорядоченной
последовательности, мы анализируем следующие возможные ситуации.
1)
Если новый отрезок пересекается с закрашиваемым отрезком (его левая
координата не больше ![]() координаты правого конца закрашиваемого
отрезка), то новым правым концом закрашиваемого сейчас отрезка становится более
правый дз концов закрашиваемого и нового отрезков.
координаты правого конца закрашиваемого
отрезка), то новым правым концом закрашиваемого сейчас отрезка становится более
правый дз концов закрашиваемого и нового отрезков.
2)
![]()
![]()
![]()
![]() Если новый отрезок не пересекается с закрашиваемым
отрезком, то закраска предыдущего отрезка закончена, его длина суммируется с
длиной уже закрашенной части, а закрашиваемым отрезком становится новый
отрезок.
Если новый отрезок не пересекается с закрашиваемым
отрезком, то закраска предыдущего отрезка закончена, его длина суммируется с
длиной уже закрашенной части, а закрашиваемым отрезком становится новый
отрезок.
Процесс продолжается до тех пор, пока не будут просмотрены все отрезки. После этого длина последнего закрашенного отрезка суммируется с длиной ранее закрашенной части.
![]() 17. Основная идея состоит в том, чтобы не
использовать операцию умножения двух чисел. Если числа натуральные, то одна из
пар должна содержать максимальное и минимальное числа. Рассуждая таким образом
для оставшихся чисел, приходим к простому алгоритму. Сортируем числа в порядке
неубывания. Тогда пары состав
17. Основная идея состоит в том, чтобы не
использовать операцию умножения двух чисел. Если числа натуральные, то одна из
пар должна содержать максимальное и минимальное числа. Рассуждая таким образом
для оставшихся чисел, приходим к простому алгоритму. Сортируем числа в порядке
неубывания. Тогда пары состав![]() ляют первое и последнее числа, второе и
предпоследнее и т. д. Ситуация немного изменяется, если числа целые. В этом
случае возможны три варианта:
ляют первое и последнее числа, второе и
предпоследнее и т. д. Ситуация немного изменяется, если числа целые. В этом
случае возможны три варианта:
1) Произведение
равно О. В этом случае существует хотя бы N нулевых элементов. Поэтому пары бу![]() дут
организованы из одного ненулевого элемента и одного нулевого или из двух
нулевых элементов.
дут
организованы из одного ненулевого элемента и одного нулевого или из двух
нулевых элементов.
llO
2) Произведение
положительно. В этом случае пере![]() множаются положительные числа с
положительными, а отрицательные —с отрицательными по
множаются положительные числа с
положительными, а отрицательные —с отрицательными по ![]() правилу, как и в
случае с натуральными числами.
правилу, как и в
случае с натуральными числами.
З) Произведение отрицательно. В этом случае перемножается минимальное положительное число с минимальным отрицательным и т. д.
для определения ситуаций достаточно подсчитать количество нулевых, положительных и отрицательных элементов.
Если есть нулевые элементы, то возможен только вариант 1). Если количество положительных элементов не равно количеству отрицательных, то возможен только вариант 2). В других случаях возможна ситуация 2) и З).
Для определения знака произведения рассмотрим четыре элемента
массива: максимальный положительный (пусть это а), минимальный положительный
(Ь), минимальный отрицательный (с), максимальный отрицательный (d). Понятно,
что решением могут быть только пары (а, Ь), (с, d) или (а, d), (Ь, с). Если а *
—с, то в случае —с в паре с элементом а должен быть меньший по модулю из
элементов Ь и d, а если —с, то — больший по модулю. В случае, если а = —с и Ь—
= —d, эта четверка не дает никакой информации о знаке произведения, поэтому
можно перейти к следующей четверке чисел и т. д., пока не будет установлен знак
произведения. Если же просмотрены все числа, а знак не ![]() установлен, то он
может быть как плюс, так и минус.
установлен, то он
может быть как плюс, так и минус.
![]() 18, Чтобы сумма произведений пар была
максимальна (минимальна), необходимо упорядочить наборы А и В
18, Чтобы сумма произведений пар была
максимальна (минимальна), необходимо упорядочить наборы А и В ![]() одинаковым
(различным) образом, и пары будут составлять элементы, стоящие на одинаковых
позициях в упорядоченных наборах. Это следует из того, что если
одинаковым
(различным) образом, и пары будут составлять элементы, стоящие на одинаковых
позициях в упорядоченных наборах. Это следует из того, что если ![]() и c<d, то
ac+bd>ad+bc.
и c<d, то
ac+bd>ad+bc.
19. Предположим, что среди пяти чисел нет одинаковых (случай
совпадающих чисел рассматривается анало![]() гично. В дальнейшем будем обозначать
операцию сравнения значком «:». Например, 5:3 означает, что мы
гично. В дальнейшем будем обозначать
операцию сравнения значком «:». Например, 5:3 означает, что мы ![]() сравниваем
пятое и третье числа. Запись означает, что пятое число меньше третьего.
сравниваем
пятое и третье числа. Запись означает, что пятое число меньше третьего. ![]()
Сначала выполним операции : 2, 3:4. При необходимости,
перенумеровывая числа, получаем, что 1 ![]() 3<4. Далее
выполняем операцию 1 Опять же при необходимости, перенумеровывая числа,
получаем I
3<4. Далее
выполняем операцию 1 Опять же при необходимости, перенумеровывая числа,
получаем I ![]() Выполняем операцию 3:5. При этом возможны
следующие ситуации:
Выполняем операцию 3:5. При этом возможны
следующие ситуации:
1) 3>5. Подводя итог четырех
проделанных операций сравнения, имеем: l <2; ![]() 5<3.
5<3.
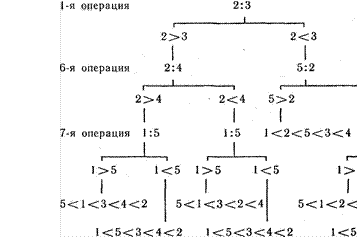
![]()
![]() Сравниваем 4 и 5. пусть 4<5. тогда
1<2;
Сравниваем 4 и 5. пусть 4<5. тогда
1<2;
Выполняем 2:4. В зависимости от
результата делаем либо 2:3, либо 2:5. Оставшиеся варианты ![]() рассматриваем
аналогично.
рассматриваем
аналогично.
20. Без потери общности предположим, что
элементы ![]() массива А упорядочены в возрастающем
порядке (во множестве нет дублирующихся элементов, поэтому мас
массива А упорядочены в возрастающем
порядке (во множестве нет дублирующихся элементов, поэтому мас![]() сив А
упорядочен именно в возрастающем, а не только
сив А
упорядочен именно в возрастающем, а не только
112
B Hey6b1Ba}0111eM nopHÄKe). ECJIM 9T0 He TaK, TO A06aB.nneM B nporpaMMY 110AnporpaMMY COPTHPOBKH.
ECJIH CBOÜCTBO ( * ) Bb1110JIH%eTCH [1011MHO>KeCTBa B, TO OHO Bblr10J11--1HeTC51 H Tpex HaH60J1b1UHX no BeJIW-1HHe 9J1eMeHTOB B. 06paTH0, H3 BblflOJIHHMOCTM ( * ) Tpex MaKCHMaJ1bHb1X 3J1eMeHTOB B cJ1emyeT BblflOJIHHMOCTb ( * )
H AJIH B. Mbl 6YÅeM BK.moqaTb B
B B nopflAKe HX B03pacTa![]() 3,neMeHTb1 H3 A M np0BepHTb Tpex MaKCUMaJ1bHb1X
3,neMeHTb1 H3 A M np0BepHTb Tpex MaKCUMaJ1bHb1X
Bblr10J11--1e1--fHe YCJIOBH%![]()
21. a) HYCTb B nepervreHH0i MaxEndHere
xpaHHTCfl ![]() cyMMa 3JRMeHTOB MaKCHMaJ16HOPO 110ÅBeKTOPa,
3aKaHMHBamuetOC% B H03HUHH Toro MT06b1
cyMMa 3JRMeHTOB MaKCHMaJ16HOPO 110ÅBeKTOPa,
3aKaHMHBamuetOC% B H03HUHH Toro MT06b1 ![]() MaxEndHere Havana xpa-
MaxEndHere Havana xpa-
![]() HHTb CYMMY 3J1eMeHTOB
MaKCHMaJ1bH01'0 110ABeKTopa, OKaHYHBam.-.uePOC51 B H03HLIHH i, He06x0AMMO
Bb1110JIHHTb cJ1eAYK)1.uyK) or-lepaumo Til)HcBauBaHH51:
HHTb CYMMY 3J1eMeHTOB
MaKCHMaJ1bH01'0 110ABeKTopa, OKaHYHBam.-.uePOC51 B H03HLIHH i, He06x0AMMO
Bb1110JIHHTb cJ1eAYK)1.uyK) or-lepaumo Til)HcBauBaHH51:
MaxEndHere•. max (MaxEndHere+A [i], A [i]);
a ÅJIH TOPO YT06b1 HaiTH MaKCHMaJ1bHYK) cyMMY MaxSoFar 3J1eMeHTOB 110ABeKTopa, BCTPeTHBU1erocH no n03HLIHH i, Hauw BblflOJIHHTb onepaumo•.
MaxS0Far•.
![]() MaxEndHere).
MaxEndHere).
11porpaMMa:
MaxS0Far•.![]()
MaxEndHere•. —A [11;
MaxEndHere•. ![]()
6) noHCKa MHHHMaJ1bHOä CYMMb1 Mbl
MOM-CM ![]() cHaqaJ1a YMHO>KHTb BCe 3J1eMeHTbl MaCCVIBa A Ha
cHaqaJ1a YMHO>KHTb BCe 3J1eMeHTbl MaCCVIBa A Ha
113
—1, а затем искать, как и в пункте а), максимальную сумму.
в) Определим массив С [О..К] такой, что C [l]+ + + А [Ц, С Заметим, что
![]()
Сумма S (М, N) элементов вектора А [М]+... + А [N] равна
нулю, если С [М— l]— С Исходя из этого соображения, возьмем массив С,
отсортируем его, затем найдем минимальную по модулю разность двух соседних
элементов отсортированного массива (т. е. найдем два ![]() наименее отличающихся
элемента массива С). Эта разность как раз и будет наиболее близким к нулю
значением суммы S(M, М).
наименее отличающихся
элемента массива С). Эта разность как раз и будет наиболее близким к нулю
значением суммы S(M, М). ![]()
г) Как и в предыдущем пункте, сформируем массив С, затем его отсортируем. Нам надо найти в этом массиве два элемента C[i] и С [Л, значение разности которых наиболее близко к Р. Пусть массив С упорядочен по неубыванию, и i и ј — индексы текущих просматриваемых элементов массива С.
i:==![]()
MinSoFar.• (С ![]() {Текущее значение минимальной разности}
while
{Текущее значение минимальной разности}
while ![]() and = К) do begin if ј (если это
не один и тот же элемент массива С) then MinSoFar: =min (MinSoFar, abs (С [ј]—С
[i]—P));
and = К) do begin if ј (если это
не один и тот же элемент массива С) then MinSoFar: =min (MinSoFar, abs (С [ј]—С
[i]—P));
![]()
then i : =i+l; {увеличиваем вычитаемое} else ј: 1;
{увеличиваем уменьшаемое} end;![]()
22. Заметим, что если мы знаем сумму S [i]+ + + Х [Н- М], то можем вычислить S [i+l] по очевидной формуле
![]()
![]() и нет необходимости во вложенном цикле для
вычисления S [i+
и нет необходимости во вложенном цикле для
вычисления S [i+![]()
23. Пусть А — это К первых элементов массива Х, а В — последних N—k. Необходимо из массива АВ получить массив ВА. Пусть есть подпрограмма REVERSE (i, ј), которая реверсирует (меняет порядок элементов на обратный) часть массива Х с индексами от i до ј. Начав с массива АВ, реверсируем часть А, получаем (Ж) В; реверсируем В, получаем (А 7 ) (Ш); реверсируем весь массив, получаем ((АЭ ( вэу= ВА.
Продемонстрируем описанный алгоритм на примере.
Пусть Х есть последовательность 1, 2, З, 4, 5, К —З:
![]() REVERSE(l,
К);
REVERSE(l,
К);
REVERSE(k+l, N);
REVERSE (1, К);
![]() АРИФМЕТИКИ
АРИФМЕТИКИ
S 1. ПОИСК ДЕЛИТЕЛЕЙ ЧИСЛА.
ПРОСТЫЕ ЧИСЛА
Натуральное число Ь называют Делителем натурального числа а,
если а представимо в виде произведения а = bc, (1) где с— натуральное число.
В этом случае говорят, что число а делится без остатка на число Ь, или, короче,
число а делится на число Ь. Из формулы (1) следует, что число а делится также
на число с, т. е. с — делитель числа а. Например, ![]() З и 5 — делители
числа 15.
З и 5 — делители
числа 15.
Число I является делителем любого натурального числа,
поскольку любое натуральное число делится на ![]() (a: l =a).
(a: l =a).
Число, делящееся на 2, называют четным; число, не делящееся на 2, называют нечетным.
Кратным числа Ь называют число а, которое делится на Ь. Множество чисел, кратных данному числу Ь, бесконечно.
В программировании для определения того, является ли число Ь делителем
числа а или нет, пользуются следующим свойством: если число а делится на число
Ь, ![]() то остаток от деления равен 0.
то остаток от деления равен 0.
если mod (а, ![]() то
то
Р:=«Делится» иначе
Р: = «Не делится» ![]() все
все
Натуральное число а, не равное 1, называется простыж, если оно делится только на себя и на 1, т. е. имеет
116
только два делителя. Натуральное число,
отличное от ![]() I и не являющееся простым, называется
составным. Другими словами, натуральное число называется составным, если оно
имеет более двух делителей. Число 1 не относится ни к простым, ни к составным
числам, поскольку имеет лишь один делитель. Наименьшим простым числом является
число 2. Это единственное четное простое число. Остальные простые числа
являются нечетными.
I и не являющееся простым, называется
составным. Другими словами, натуральное число называется составным, если оно
имеет более двух делителей. Число 1 не относится ни к простым, ни к составным
числам, поскольку имеет лишь один делитель. Наименьшим простым числом является
число 2. Это единственное четное простое число. Остальные простые числа
являются нечетными.
Для того чтобы найти делители числа а Ы, мы должны попытаться делить данное число на все отличные от числа, меньшие а. Если а не разделилось ни на одно из них, следовательно, оно является простым.
Массив В будем использовать для хранения делителей числа а,
переменную Р — для определения того, ![]() простое число или составное, переменную К
— для обозначения номера текущего делителя числа а.
простое число или составное, переменную К
— для обозначения номера текущего делителя числа а.
Р : = «простое»
![]()
: ==а
К: 2 нц для i от 2 до а —1![]() (3.2)
(3.2) 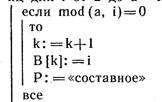 если
mod (а,
если
mod (а,
кц ![]()
После выполнения алгоритма первые К элементов ![]() массива В
будут содержать все делители числа а.
массива В
будут содержать все делители числа а.![]()
В приведенном алгоритме мы делили число а на все отличные от
1 числа, меньшие а. На самом деле делитель не может превышать а/2 (почему?).
Учет этого очевидного факта приводит к увеличению скорости работы программы в
два раза. ![]()
1 17
Алгоритм (3.2), кроме нахождения делителей числа а,
определяет, является ли число а простым или составным. Если требуется только
определить, простое число или составное, то данный алгоритм можно улучшить. В
самом деле, цикл для i от 2 до а— 1 выполняется а— 2 раза. Однако для проверки
простоты числа а достаточно выполнить данный цикл [АД] раз (ГАД] — целая часть
от корня квадратного из а). Это вытекает из следующих соображений. Если а —
число составное, его можно представить в виде ![]() где bQ,6, с Если а
делится на Ь, то оно будет делиться и на с. Если а не делится ни на одно число,
меньшее или равное АД, то оно не будет делиться ни на какое другое число.
где bQ,6, с Если а
делится на Ь, то оно будет делиться и на с. Если а не делится ни на одно число,
меньшее или равное АД, то оно не будет делиться ни на какое другое число. ![]()
Запишем алгоритм проверки, является ли число а простым:
![]() Р: = «простое» нц для
i от 2 до int (sqrt
Р: = «простое» нц для
i от 2 до int (sqrt ![]() если (mod (а, и (Ка) то
если (mod (а, и (Ка) то
Р : = «составное» все кц
![]() В цикле ДЛЯ к величине int (sqrt (а))
добавлена 1, так как значение sqrt (а) является вещественным и может
вычисляться с погрешностью.
В цикле ДЛЯ к величине int (sqrt (а))
добавлена 1, так как значение sqrt (а) является вещественным и может
вычисляться с погрешностью.
Идеей уменьшения количества выполнений цикла можно воспользоваться и для нахождения делителей числа а. Попытайтесь сделать это самостоятельно.
Алгоритм определения простого числа можно еще улучшить, если останавливаться сразу после того, когда установили, что число не является простым (т. е. если а разделилось на какое-либо число).
Р : = «простое»
![]() =int (sqrt (а
=int (sqrt (а ![]() и (mod (а,
и (mod (а,![]()
![]() кц если (mod (а, и (Ка) то
кц если (mod (а, и (Ка) то
Р : = «составное» все
* Множество простых чисел является бесконечным. Очевидно, что множество простых чисел, не превосходящих некоторого числа N, будет конечным. Возникает вопрос — как же найти эти простые числа?
![]() Можно, конечно же,
просмотреть первые N натуральных чисел и для каждого проверять, является ли оно
простым. Однако данный метод, хоть и прост с первого взгляда, не является
эффективным, так как программа будет работать очень медленно даже для небольших
N.
Можно, конечно же,
просмотреть первые N натуральных чисел и для каждого проверять, является ли оно
простым. Однако данный метод, хоть и прост с первого взгляда, не является
эффективным, так как программа будет работать очень медленно даже для небольших
N. ![]() (Можете проверить!)
(Можете проверить!) ![]()
Лучше всего делать это методом, который предложил Эратосфен Киренский (ок. 276—194 гг. до н. э.), друг Архимеда. Называется метод — решето Эратосфена.
![]() Суть метода следующая: выпишем подряд все числа от до N.
Первым стоит число 1. Оно не является простым. Вычеркнем это число. Следующее
число 2. Это простое число. Оставляем его и вычеркиваем все числа, кратные 2.
Для этого достаточно вычеркнуть каждое второе число, начиная счет с З. Первым
невычеркнутым числом будет З. Это простое число. Оставляем его и вычеркиваем
все числа, кратные З, т. е. каждое третье число, начиная счет с 4. (При счете
необходимо учитывать и ранее вычеркнутые числа, поэтому некоторые числа
вычеркиваются второй раз: такими числами будут 6, 12, 18... . )
Суть метода следующая: выпишем подряд все числа от до N.
Первым стоит число 1. Оно не является простым. Вычеркнем это число. Следующее
число 2. Это простое число. Оставляем его и вычеркиваем все числа, кратные 2.
Для этого достаточно вычеркнуть каждое второе число, начиная счет с З. Первым
невычеркнутым числом будет З. Это простое число. Оставляем его и вычеркиваем
все числа, кратные З, т. е. каждое третье число, начиная счет с 4. (При счете
необходимо учитывать и ранее вычеркнутые числа, поэтому некоторые числа
вычеркиваются второй раз: такими числами будут 6, 12, 18... . ) ![]() После этой
операции первым невычеркнутым, а значит
После этой
операции первым невычеркнутым, а значит ![]() простым, будет число
5. Оставляем это число и вычеркиваем все числа, кратные 5, т. е. каждое пятое
число,
простым, будет число
5. Оставляем это число и вычеркиваем все числа, кратные 5, т. е. каждое пятое
число, ![]() начиная счет с б. Затем переходим к
следующему невычеркнутому числу 7 и так далее. Таким способом мы вычеркиваем
все составные числа, останутся лишь простые. В таблице приведены результаты
указанных действий для 50; вычеркнутые числа подчеркнуты.
начиная счет с б. Затем переходим к
следующему невычеркнутому числу 7 и так далее. Таким способом мы вычеркиваем
все составные числа, останутся лишь простые. В таблице приведены результаты
указанных действий для 50; вычеркнутые числа подчеркнуты.
![]() 2 З 4 5
2 З 4 5
![]() 6 7 8 9 10
6 7 8 9 10
![]() 12
12![]() 15
15 ![]() 16 17 18 19 20
16 17 18 19 20
![]() 21 22 23 24 25 26 27 28 29 зо
21 22 23 24 25 26 27 28 29 зо
31 32 33 34 35 36 37 38 39 40
41 42 43 ![]() 44
44 ![]() 46 47 48 49 50
46 47 48 49 50
Метод Эратосфена получил название решета по следующим причинам. Древние греки рабочие записи вели заостренной палочкой на восковых дощечках. Такой палочкой Эратосфен прокалывал те места, где были написаны составные числа. После этого дощечка становилась похожей на решето. Применяя метод Эратосфена, как бы отсеивают, пропускают через решето все составные числа и оставляют только простые.
![]()
З. После этого найдем первое ненулевое число после числа З и будем заменять нулями все числа, кратные ему. Так продолжаем до тех пор, пока не просмотрим весь массив.
![]()
нц для i от 2 до N :первоначальное за-
![]()
![]() массива
массива
:индекс первого
: обнуляемого
: кратных текущему
![]() —
— ![]() 0)
: поиск очередного : ненулевого числа
0)
: поиск очередного : ненулевого числа
кц
Этот алгоритм работает достаточно быстро.
Для![]()
= 10 000 результат получается через З секунды (для [ВМ PS/2—286). Однако у него есть один недостаток: для хранения всех чисел требуется массив слишком большой размерности (5000 элементов для 10 000). Поэтому можно воспользоваться другим алгоритмом, который работает медленнее, однако не требует сохранения в массиве всех нечетных чисел.
В массиве будем хранить только простые числа. Вначале в массив поместим число 2. Рассматривая очередное нечетное число Х, будем делить его на предшествующие ему простые числа. И если ни на одно из предшествующих простых чисел текущее не делится, то оно само является простым. Проверку на делимость числа нужно заканчивать после того, как проверена делимость на простое число, не превосходящее [sqrt (Х)].
![]() 2
2
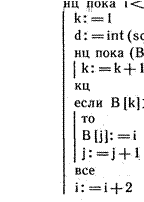 =d)
и (mod (i, В
=d)
и (mod (i, В ![]() и (К<ј)
и (К<ј)
кц
Данный алгоритм на компьютере с 286-м процессором при 10 000 выдает результат через 12 секунд. Следует обратить внимание и на необходимость введения переменной d. Выражение, значение которого присваивается переменной d, можно вычислять непосредственно в условии цикла, однако это удлинит работу программы до 100 секунд. (Проверьте и подумайте, почему так происходит.)*
Вопросы для повторения
1. Как определить, делится ли данное число а на число Ь?
2. Как найти все делители числа?
З. Как определить, является ли число простым?
4. Как получить все простые числа, не превосходящие данного числа N?
S 2. РАЗЛОЖЕНИЕ ЧИСЛА НА ПРОСТЫЕ МНОЖИТЕЛИ
Всякое число можно представить в виде произведения простых множителей, причем такое представление является единственным с точностью до порядка сомножителей. Этот факт, называемый основной теоремой арифметики, известен из курса математики 6-го класса. Напомним алгоритм разложения числа на простые множители.
Пусть число а разложено в произведение ТТ... р, ,
Находить будем по следующему алгоритму: разделим число а на наименьшее простое число 2, если остаток от деления равен 0, то и число а уменьшаем в 2 раза, т. е. а: div 2. Затем опять делим а на 2, если разделилось, то и а опять уменьшаем в два раза. Так продолжаем до тех пор, пока а делится на 2. Если число а не разделилось на 2, то пытаемся делить а на следующее простое число З. Если разделилось, то находим очередное д и уменьшаем а в З раза. Продолжаем так до тех пор, пока число делится на З. Затем пытаемся делить на 5, 7, ll, Закончим тогда, когда а = 1.
В качестве примера рассмотрим разложение на простые множители числа 2520. Запись будем производить по знакомой схеме:
25202
12602 2520 2-2-2.з.з.5-7
6302
315з
105З
355
77
Несколько изменим описанный алгоритм. Данное число будем делить на 2, а затем только на нечетные числа. Если какое-то нечетное число Х является составным, то число а на него не разделится (так как число а уже разделилось на простые числа, произведение которых равно Х, и они меньше Х). Простые множители будем хранить в массиве В, К — номер текущего простого множителя, d — число, на которое делим.
![]()
![]() К: d: нц пока
К: d: нц пока

кц
После выполнения данного алгоритма первые К элементов массива
В будут содержать простые числа, про![]() изведение которых равно а.
изведение которых равно а.
В разложении числа на простые множители могут быть равные числа. Объединяя равные множители, из формулы (2) получим формулу вида
![]() а
а
a=pl ...рК, (3)
![]() где Pl, Р2, —
различные простые числа, щ, а2, ..., т — некоторые натуральные числа. Каждое из
ai показывает, сколько раз входит множитель р, в разложение числа а.
Произведение в правой части равенства (З) называют каноническим разложением
натурального числа а.
где Pl, Р2, —
различные простые числа, щ, а2, ..., т — некоторые натуральные числа. Каждое из
ai показывает, сколько раз входит множитель р, в разложение числа а.
Произведение в правой части равенства (З) называют каноническим разложением
натурального числа а.
![]() Так, число 2520 из нашего примера будет
записано следующим образом:
Так, число 2520 из нашего примера будет
записано следующим образом:![]()
Вопросы для повторения
1. Всякое ли число при разложении на простые множители имеет больше одного множителя?
2. Как разложить число на простые множители?
З. Почему не применяют в информатике алгоритм разложения на простые множители, известный из курса математики?
4. Что такое каноническое разложение?![]()
S З. ПОИСК НАИБОЛЬШЕГО ОБЩЕГО
ДЕЛИТЕЛЯ (НОД) И НАИМЕНЬШЕГО ![]() ОБЩЕГО КРАТНОГО (НОК)
ОБЩЕГО КРАТНОГО (НОК)
Если а и Ь— два натуральных числа и если число с таково, что а делится на с и Ь делится на с, то число с называют общим делителем чисел а и Ь. Произвольные два числа всегда обладают ОбЩИЯ Делитележ. Таким делителем является число 1. Если других общих делителей нет, то числа а и Ь называют взаимно простыми.
3.1. поиск нод
![]()
(НОД) чисел а и Ь, если d является общим делителем чисел а и Ь; d делится на любой другой общий делитель. Другими словами, d — наибольший из всех общих делителей чисел а и Ь.
![]()
![]() В курсе
математики приводился следующий алгоритм нахождения НОД. Необходимо разложить
числа а и Ь на простые множители и затем выбрать те из них, которые входят и в
одно и в другое разложение. Рассмотрим пример: НОД (2520, 2475).
В курсе
математики приводился следующий алгоритм нахождения НОД. Необходимо разложить
числа а и Ь на простые множители и затем выбрать те из них, которые входят и в
одно и в другое разложение. Рассмотрим пример: НОД (2520, 2475).
![]() 2520 2
2520 2
1260 2
630 2
315 з
105 з
35 5
7 7
![]() Общие множители подчеркнуты. нод (2520,
Общие множители подчеркнуты. нод (2520,![]()
![]()
Данный алгоритм на практике обычно не применяется, так как
разложение числа на простые множители уже является достаточно трудоемкой
задачей, а ведь еще потребуется найти среди них одинаковые. Поэтому очень часто
для нахождения НОД применяют метод, который ![]() называется алгоритмом
Евклида.
называется алгоритмом
Евклида.
Это один из самых древних и популярных алгоритмов. Он описан еще в «Началах» Евклида.
![]() Прежде чем описать сам алгоритм, укажем несколько свойств
НОД, на которые опирается алгоритм Евк
Прежде чем описать сам алгоритм, укажем несколько свойств
НОД, на которые опирается алгоритм Евк![]() лида.
лида.
Пусть а и Ь — отличные от нуля натуральные числа, причем a>b, тогда:
1)
НОД (а, ![]() (а—Ь, Ь);
(а—Ь, Ь);
2)
НОД (а,![]()
3) нод (а, ока.
Свойства 2) и З) являются очевидными. ![]() П р и м е ч а н и е. Докажем свойство
1).
П р и м е ч а н и е. Докажем свойство
1).
![]() Свойство будет доказано, если мы
установим, что множество общих
Свойство будет доказано, если мы
установим, что множество общих ![]() делителей чисел а и Ь совпадает с множеством общих делителей чисел
делителей чисел а и Ь совпадает с множеством общих делителей чисел ![]() и Ь, т. е. всякий общий делитель Х
чисел а и Ь является делителем чисел а—Ь и Ь, и наоборот. Если Х — делитель а и
Ь, то а— КХ и b=lX для некоторых К и l. Тогда Х, т. е. Х является общим
делителем чисел а—Ь и Ь. Наоборот, пусть и Ь=пХ для некоторых т и п. Складывая,
получаем Х. Таким образом, Х является общим делителем а и Ь.
и Ь, т. е. всякий общий делитель Х
чисел а и Ь является делителем чисел а—Ь и Ь, и наоборот. Если Х — делитель а и
Ь, то а— КХ и b=lX для некоторых К и l. Тогда Х, т. е. Х является общим
делителем чисел а—Ь и Ь. Наоборот, пусть и Ь=пХ для некоторых т и п. Складывая,
получаем Х. Таким образом, Х является общим делителем а и Ь.
Перечисленные равенства подсказывают идею алгоритма нахождения НОД: нужно от большего отнимать меньшее, до тех пор, пока числа не станут равными
(свойство после чего НОД найдется по свойству 2). Пример: найти НОД (530, 155), а=5ЗО, 155.
![]() а
а
|
|
|
|
|
|
||||||||||||||
|
|
15 ![]()
5 ![]()
5 5 Алгоритм будет следующим:
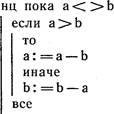
кц
![]()
Если проанализировать работу данного алгоритма, то можно
заметить, что одно и то же число нужно отнимать несколько раз. Этого можно
избежать, если вместо нескольких вычитаний находить остаток от деления большего
числа на меньшее (подумайте почему). В этом случае свойство 1) можно записать в
виде: НОД (а, ![]() = НОД (а mod Ь, Ь). Для окончания работы
алгоритма нужно воспользоваться свойством З).
= НОД (а mod Ь, Ь). Для окончания работы
алгоритма нужно воспользоваться свойством З). ![]()
Пример: Найти НОД (530, 155), а=5ЗО, Ь— 155. а
530 155
65 155
65 25
15 25
15![]()
5 10
5 ![]()
Алгоритм будет выглядеть следующим образом:
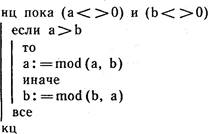
![]() если а
если а ![]() то NOD:
то NOD:![]()
иначе
NOD: ==а все
Последний оператор ЕСЛИ можно заменить оператором NOD: =a+b. Подумайте почему.
3.2. поиск нок
Если а и Ь— два натуральных числа и если число с таково, что с делится на а и с делится на Ь, то число с называют общим кратным чисел а и Ь. Произвольные два числа всегда обладают общим кратным. Таким кратным является число, равное произведению ab.
Число d называют наименьшим общим кратным (НОК) чисел а и Ь, если d является общим кратным чисел а и Ь; на d делится любое другое общее кратное. Другими словами, d — наименьшее из всех общих кратных чисел а и Ь.
Для нахождения НОК можно воспользоваться алгоритмом, известным из курса математики. Нужно разложить числа а и Ь на простые множители, а затем из двух разложений выбрать те сомножители, которые входят хотя бы в одно разложение. Пример: НОК (52, 65).
![]() 52
52 ![]() 2 65 5
2 65 5
26 2 13 13
13 13![]()
Однако пользоваться этим алгоритмом на практике не следует
(причины описаны выше). Для нахождения НОК можно воспользоваться следующим
свойством: НОК (а, ![]() (а, Ь) (докажите самостоятельно). Для
нахождения НОД следует воспользоваться алгоритмом Евклида.
(а, Ь) (докажите самостоятельно). Для
нахождения НОД следует воспользоваться алгоритмом Евклида.
Вопросы для повторения
1, Что такое НОД?
2, Какие способы вычисления НОД вам известны?
З. Что такое НОК?
4. Как найти НОК трех чисел?
S 4. ПРЕДСТАВЛЕНИЕ ЧИСЕЛ.
ВЫДЕЛЕНИЕ ЦИФР ЧИСЛА
В десятичной системе счисления, как и в любой другой позиционной системе счисления, натуральное число может быть записано в виде суммы разрядных слагаемых, т. е. в виде суммы единиц, десятков, сотен, тысяч и т. д. Так, например, число 6487 содержит 7 единиц, 8 десятков, 4 сотни и 6 тысяч и может быть записано в виде выражения:
6487=6-1000+4. 100+8- 10+7.
![]()
![]() Цифры 6, 4, 8, 7 являются цифрами числа 6487, а 1000, 100,
— разрядные единицы. Каждая разрядная единица является степенью числа 10,
поэтому представление числа в виде суммы разрядных слагаемых чаще записывают
так:
Цифры 6, 4, 8, 7 являются цифрами числа 6487, а 1000, 100,
— разрядные единицы. Каждая разрядная единица является степенью числа 10,
поэтому представление числа в виде суммы разрядных слагаемых чаще записывают
так:
6487_6- 103 +4- 102 +8- 10!+7- 100 .
![]() Вид числа в левой части равенства будем
называть обычным представлением числа в десятичной форме. При написании
программ такие числа хранятся в стандартных числовых типах, например: ЦЕЛ, ВЕЩ.
При работе с числами в обычном представлении мы не имеем возможности
непосредственно обращаться к цифрам этого числа, однако иногда это бывает
необходимо. Например, если требуется вычислить значение выражения, которое не
помещается в стандартном числовом типе (100!), то число представляют в виде
массива цифр. Такое представление будем называть табличным представлением
числа.
Вид числа в левой части равенства будем
называть обычным представлением числа в десятичной форме. При написании
программ такие числа хранятся в стандартных числовых типах, например: ЦЕЛ, ВЕЩ.
При работе с числами в обычном представлении мы не имеем возможности
непосредственно обращаться к цифрам этого числа, однако иногда это бывает
необходимо. Например, если требуется вычислить значение выражения, которое не
помещается в стандартном числовом типе (100!), то число представляют в виде
массива цифр. Такое представление будем называть табличным представлением
числа.
5 Информатика. 8—9 ка.
Размещение цифр числа в массиве возможно двумя способами. Связано это с тем, что разряды чисел нумеруются справа налево, а число читается слева направо, поэтому цифры числа можно располагать в массиве, начиная с первой (старший разряд), а можно — начиная с последней (младший разряд). Порядок, при котором цифра старшего разряда является первым элементом массива, назовем прямым. Обратным вазовем порядок, при котором первый элемент в массиве является цифрой младшего разряда.
Можно задавать число и как литерную величину, тогда мы получим доступ к каждой отдельной цифре, однако с ними, без преобразования в числовой тип, нель• зя выполнять арифметические операции.
Рассмотрим способы преобразования обычного представления числа в табличное и наоборот.
4.1. Преобразование числа из обычного представления в табличное
Пусть задано число в обычном представлении, необходимо получить табличное представление данного числа.
Как видно из представления числа в виде суммы разрядных слагаемых, каждое слагаемое, кроме последнего, разделится на 10 без остатка. Поэтому остаток от деления числа на l0 будет равен последней цифре числа. Эту цифру мы помещаем в массив. Если мы размещаем в массиве цифры числа, начиная с последней, то первому элементу массива присваивается значение полученной цифры. Если размещаем цифры, начиная с первой, то полученную цифру помещаем в элемент массива с индексом, равным количеству цифр в числе (количество цифр необходимо подсчитать до того, как начнем получать сами цифры). Далее находим целую часть от деления исходного числа на 10 (или, говоря другими словами, отбрасываем последнюю цифру числа) и снова на-
![]() ходим остаток от деления данного числа на
10, это и будет следующая цифра. Так продолжаем до тех пор, пока в числе не
останется ни одной цифры.
ходим остаток от деления данного числа на
10, это и будет следующая цифра. Так продолжаем до тех пор, пока в числе не
останется ни одной цифры.
Данный алгоритм размещает цифры числа в массив в обратном порядке. Для хранения цифр числа N будем использовать массив В, К — номер текущей цифры в массиве В.
![]() К:
К:
10)![]()
Первые К элементов массива В содержат цифры числа М, записанные в обратном порядке.
Изменим алгоритм для получения цифр числа в прямом порядке.
К:![]()
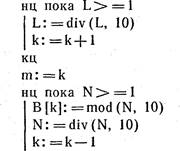
кц
Первый цикл ПОКА считает количество цифр в числе, второи
получает цифры числа. Переменная L служит для того, чтобы сохранить значение
исходного числа, так как внутри цикла переменная изменяет свое значение. Если
бы в первом цикле использовалась ![]() переменная М, то после выполнения цикла ее
значение равнялось бы 0 (почему?) и второй цикл не выполнился бы ни разу. В
переменной т сохраняется количество цифр числа, что, вообще говоря, не всегда
необходимо.
переменная М, то после выполнения цикла ее
значение равнялось бы 0 (почему?) и второй цикл не выполнился бы ни разу. В
переменной т сохраняется количество цифр числа, что, вообще говоря, не всегда
необходимо.
4.2. Преобразование
табличного представления числа в обычное ![]()
Решим обратную задачу, т. е. получим обычное представление числа из табличного.
Пусть некоторое число а задано своими цифрами:
а = а1И2аз а![]()
Черта сверху обозначает, что щ, (12, аз, ![]() цифры числа а (щ — цифра старшего
разряда). Запишем это число в виде суммы разрядных слагаемых:
цифры числа а (щ — цифра старшего
разряда). Запишем это число в виде суммы разрядных слагаемых:
![]() 1 -р 02. 2 +
аз. 3 + ... -Кап _ 1 . (4)
1 -р 02. 2 +
аз. 3 + ... -Кап _ 1 . (4)
Для того чтобы получить значение числа а, необходимо вычислить значение выражения, стоящего в правой части равенства (4). Для этого проделаем следующие преобразования: вынесем 10 за скобки из тех слагаемых, для которых это возможно.
![]() 1 + ф.
1 + ф.
Затем с выражением в скобках проделаем то же самое, т. е. вынесем 10 за скобки из тех слагаемых, для которых это возможно. Продолжим действовать таким образом до тех пор, пока это будет возможно:
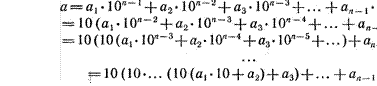
![]()
Теперь для вычисј1ения значения числа а достаточно:
1)
первую цифру числа умножить на 10 и к произве![]() дению прибавить вторую
цифру;
дению прибавить вторую
цифру;
2) полученную сумму умножить на l0 и прибавить следующую цифру;
З) пункт 2) выполнять до тех пор, пока не используем все заданные цифры числа.
Описанный выше алгоритм называется схемой Горнера. Работа алгоритма рассмотрена для случая, когда цифры числа расположены в массиве в прямом (щ — цифра старшего разряда) порядке.
Число будем получать в переменной а. Цифры числа хранятся в массиве В (элемент В [1] содержит цифру старшего разряда).
нц для i от I до N
![]()
Для получения числа а, цифры которого заданы в обратном порядке (первый элемент массива содержит цифру младшего разряда), можно воспользоваться схемой Горнера, начиная обработку с последнего элемента массива.
Можно воспользоваться и другим алгоритмом. Каждая цифра
должна умножаться на соответствующую ей разрядную единицу: первая на 1, вторая ![]() третья
— на 100 и т. д. Каждая следующая разрядная единица в 10 раз больше предыдущей.
Число а будем накапливать следующим образом: будем брать очередную цифру,
умножать ее на соответствующую ей разрядную единицу и прибавлять полученное
произведение к уже накопленному числу. Разрядную единицу увеличим в 10 раз. Так
продолжаем до тех пор, пока не используем все цифры числа.
третья
— на 100 и т. д. Каждая следующая разрядная единица в 10 раз больше предыдущей.
Число а будем накапливать следующим образом: будем брать очередную цифру,
умножать ее на соответствующую ей разрядную единицу и прибавлять полученное
произведение к уже накопленному числу. Разрядную единицу увеличим в 10 раз. Так
продолжаем до тех пор, пока не используем все цифры числа.
В переменной будем хранить значение разрядной единицы, цифры числа будем хранить в массиве В.
133
нц для i от I до N![]()
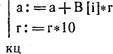 (3.13)
(3.13)
Проанализируйте алгоритмы (3.12) и (3.13) на скорость работы (посчитайте количество выполненных арифметических операций).
Вопросы для повторения
1. Какой порядок расположения цифр числа в массиве называется прямым? Обратным?
2. Как получить цифры числа в обратном порядке? В прямом порядке?
З, Как получить число из массива цифр? 4, Что такое схема Горнера?
S 5. ПЕРЕВОД ЧИСЕЛ ИЗ ОДНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДРУГУЮ
Задачи перевода чисел из одной системы счисления в другую можно разделить на две группы: перевод из десятичной системы счисления в какую-то другую и из какой-то в десятичную (рассматриваем только позиционные системы счисления). Если требуется, например, пе: ревести число из троичной системы счисления в семеричную, это можно сделать через десятичную систему счисления. Если делать это напрямую, то придется моделировать арифметические действия либо в троичной, либо в семеричной системе счисления.
Для записи числа в любой системе счисления, кроме десятичной, мы будем пользоваться только табличным представлением числа.
Алгоритм перевода числа из десятичной системы счисления в
какую-то другую известен. Нужно разделить число на основание системы счисления,
в которую переводят, и найти остаток. Если целая часть частного получилась не
равной нулю, то ее делят на основание системы счисления. Так продолжают до тех
пор, пока целая часть частного не станет равной нулю. Затем выписывают остатки
в порядке, обратном их получению. Эти остатки являются цифрами искомого ![]() числа.
числа.
![]() П р и м ер. Переведем число 345 в
семеричную систему счисления.
П р и м ер. Переведем число 345 в
семеричную систему счисления.
325 | 7
28
|
7 |
|
|
45
42
42 6 1 7
4 ![]() з
з
6
Остатки выделены жирным шрифтом.
![]()
![]() 6437.
6437.
По аналогии с записью числа в виде суммы разряд-
![]()
ных слагаемых в десятичной системе счисления, в семеричной системе счисления число можно записать следующим образом:
6437
= 6-72+4-71 з . 70. ![]()
Вообще натуральное число а в позиционной . системе счисления может быть записано следующим образом:
а • рп • рп 2 аз • рп¯З —1— + ап_ р + а,п, (5)
![]() где щ, щ, аз, ап —- цифры числа а, р —
основание системы счисления, причем К акр, 1
где щ, щ, аз, ап —- цифры числа а, р —
основание системы счисления, причем К акр, 1 ![]()
![]() Запись (5) отличается от (4) только тем,
что основа
Запись (5) отличается от (4) только тем,
что основа![]() ние десятичной системы счисления 10
заменим на про
ние десятичной системы счисления 10
заменим на про![]() извольное число р (основание новой системы
счисления).
извольное число р (основание новой системы
счисления).
135
Цифры числа в новой системе счисления можем получать, пользуясь алгоритмом (3.10), опять же заменив число 10 числом р. Цифры числа, записанного в системе счисления с основанием р, будут храниться в массиве В в обратном порядке.
Запишем алгоритм перевода числа N из десятичной системы счисления в систему счисления с основанием р:
нц пока
В [Ю: =mod (N, р) (3.14)
N: =div (N, р) кц
С помощью алгоритмов (3.10) и (3.12) можно осуществить и перевод из какой-то системы счисления (с основанием меньше 10) в десятичную. Для этого нужно вычислить значение выражения (5) (алгоритм (3.12) или (3.13), заменяя 10 на р). Число получим в обычном представлении. Табличное представление можно получить, применив алгоритм (3.10) к полученному результату.
Этот алгоритм сформулируйте самостоятельно.
Вопросы для повторения
1. Как перевести число из десятичной системы счисления в какую-то другую?
2. Как перевести число в десятичную систему счисления?
S 6. ДЕЛИМОСТЬ ЧИСЕЛ
Для определения, делится ли одно число на другое, нужно, как упоминалось выше, найти остаток от деления одного числа на другое и проверить, равен ли он нулю. Если остаток равен нулю, то число делится, если не равен нулю — нет. Таким образом, проверка на дели-
мость сводилась к нахождению остатка от деления одного числа на другое. Для чисел в обычном представлении остаток находится с помощью стандартной операции mod. При решении этой задачи вручную мы делим одно число на другое «в столбик».
Рассмотрим, как найти остаток от деления числа, заданного таблично, на число в обычном представлении.
![]()
В десятичной системе счисления число представимо в виде (4) (S 4, п. 4.2):
![]()
где щ, а2, аз, . . . , ап цифры числа а, причем 10,
Пусть нам требуется найти остаток от деления числа а на число т.
Прежде чем это делать, укажем на некоторые свойства остатков. Пусть с, d, п — некоторые натуральные числа, тогда:
1) (c-Fd) mod п=((с mod mod п)) mod п;
2) mod
n—c (d mod п) mod п==((с mod п) d) mod а; З) cd mod ![]() mod п) с) mod п.
mod п) с) mod п.
П ри меч а н ие. Докажем свойство 1).
Пусть c} = с div п, 02 = = с mod п, Щ —d div п, d2=d mod п; тогда d=dl •п+Щ;
(c+d) mod п , п + c2+dl , п + Щ) mod +dl) п + ф) mod п = ![]() (ct2+d2) mod mod mod п)) mod п.
(ct2+d2) mod mod mod п)) mod п.
Доказательства свойств 2) и З) аналогичны. Попытайтесь доказать их самостоятельно.
Найдем остаток от деления числа а (представление (4), п. 4.2) на число т, пользуясь свойствами l) и 2) (сначала применим свойство 1), затем к каждому слагаемому свойство 2)):
а mod nt (ас lOH l+ar 10п 2 + аз. 3+... + mod 1 ) mod т +
+ (ау 2) mod n•l+
+ + (ап 1 • 10) mod т -Рап
mod т) mod т![]()
((al ( 10 'l l mod m)mod ![]() 2 mod m) mod
2 mod m) mod![]()
+ -F(an_] (10 mod т) mod m)-Fan mod т) mod т.
Из последнего равенства вытекает алгоритм нахождения остатка. Находим остаток от деления очередной разрядной единицы на число т, пользуясь свойством З). Умножаем полученное число на значение цифры, соответствующей данной разрядной единице, прибавляем к тому, что получили на предыдущих шагах, и снова находим остаток от деления на т. Так продолжаем до тех пор, пока не используем все цифры числа а.
Значение искомого остатка будем накапливать в переменной s, значение остатка разрядной единицы — в переменной r, цифры числа будут храниться в массиве В (в обратном порядке, т. е. элемент В соответствует цифре младшего разряда).
![]() для i от до N
для i от до N ![]() mod
((s+B [iFr), т)
mod
((s+B [iFr), т) ![]() mod (г*1о, т)
mod (г*1о, т)![]()
![]() Алгоритм (3.15) можно применять для
получения остатка от деления числа а на число т и в том случае, если число а,
заданное в виде массива цифр, записано в любой позиционной системе счисления
(цифры числа должны быть записаны своими десятичными аналогами). Для этого
достаточно число 10 в алгоритме (3.15) заменить основанием системы счисления р.
Остато»к от деления будет получен в десятичной системе счисления. Если есть
необходимость, его можно перевести в систему счисления с основанием р.
Алгоритм (3.15) можно применять для
получения остатка от деления числа а на число т и в том случае, если число а,
заданное в виде массива цифр, записано в любой позиционной системе счисления
(цифры числа должны быть записаны своими десятичными аналогами). Для этого
достаточно число 10 в алгоритме (3.15) заменить основанием системы счисления р.
Остато»к от деления будет получен в десятичной системе счисления. Если есть
необходимость, его можно перевести в систему счисления с основанием р. ![]()
Для получения остатка от деления можно также воспользоваться схемой Горнера. Для этого представление числа ((4), п. 4.2) необходимо преобразовать по схеме Горнера, а затем применить свойства остатков так, как это сделано выше. (Данный алгоритм напишите самостоятельно.)
![]() Вопросы для повторения
Вопросы для повторения
1. Какие свойства остатков вы знаете?
2. Как найти остаток от деления числа, заданного в виде массиза цифр, на число, заданное непосредственно?
З. Как можно использовать схему Горнера для нахождения
остатка от деления числа, заданного в виде массива цифр, ![]() на число, заданное непосредстаенно?
на число, заданное непосредстаенно?
S 7. ДЕЙСТВИЯ С МНОГОЗНАЧНЫМИ (БОЛЬШИМИ)
ЧИСЛАМИ
В данном пункте под многозначными числами мы будем понимать числа, заданные табличным представлением в десятичной системе счисления.
Работа с многозначными числами предполагает моделирование арифметических действий над двумя числами, заданными массивами свои.х цифр.
Алгоритмы работы с такими массивами будут напоминать знакомые из курса математики действия в столбик.
Пусть два положительных числа А и В заданы как массивы цифр, причем A [l] и В [Ц содержат цифры младшего разряда. (Подумайте, почему такой порядок цифр для данной задачи удобнее.) Число А состоит из N цифр, а число В — из М цифр.
7.1. Сложение многозначных чисел
Найдем сумму чисел А и В. Будем складывать элементы массивов
с одинаковыми номерами и хранить полученные результаты, как элементы массива С.
Если на каком-то шаге получим 10, то на месте С ![]() оставляем остаток от
деления C[i] на 10 (количество единиц данного разряда), а к элементу С [i+ 1]
прибавим
оставляем остаток от
деления C[i] на 10 (количество единиц данного разряда), а к элементу С [i+ 1]
прибавим ![]() (перенос 1 в следующий разряд).
(перенос 1 в следующий разряд).
Если число А состоит из N цифр, а число В — из М цифр, то число С имеет либо тах (М, М) цифр, либо
139
тах (N, M)-F l цифру. Обозначим через К величину max(N, М) + 1.
Перед выполнением сложения следует дополнить незначащими нулями число с меньшим количеством цифр так, чтобы количество цифр уравнялось. Этого можно достигнуть и обнулив массивы А и В до ввода цифр.
Алгоритм сложения двух многозначных чисел будет следующим:
если
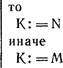
все
![]()
нц для i от I до К
![]()
нц для i от I до К
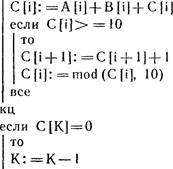
все
После выполнения данного алгоритма в первых К элементах массива С будет храниться сумма чисел А и В, С [1] — цифра младшего разряда. Последняя проверка позволяет убрать незначащий нуль из старшего разряда числа С.
[40
7.2. Вычитание многозначных чисел
Для определенности будем считать, что А Если нет, то необходимо поменять числа местами, а результат сделать отрицательным. (Подум айте, как определить, какое из чисел больше.)
Если число А состоит из N цифр, тогда число В не может иметь более чем N цифр. Разность будет содержать не более чем N цифр.
Найдем разность чисел А и В. Будем вычитать элементы массива
В из элементов массива А с соответствующими номерами. Полученные результаты
будем хранить в массиве С. Если на каком-то шаге получим С ![]()
![]() то
к элементу C[i] прибавляем 10, а от элемента С [Н- l] отнимаем (забираем из
следующего разряда).
то
к элементу C[i] прибавляем 10, а от элемента С [Н- l] отнимаем (забираем из
следующего разряда).
Алгоритм будет следующим:
кц нц для i от I до N
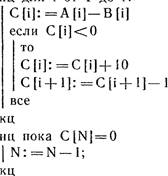
Последний цикл позволяет убрать незначащие нули в начале числа С. Данный алгоритм после некоторых дополнений можно применять для вычитания чисел с разными знаками. Подумайте, что нужно изменить.
7.3*. Произведение многозначных чисел![]()
Алгоритм нахождения произведения будет заключаться в
следующем: число А будем поочередно умно![]() жать на каждую из цифр
числа В. Полученный на
жать на каждую из цифр
числа В. Полученный на ![]() данном шаге результат будем накапливать в
массиве С, прибавляя к тому, что уже получили на предыдущих шагах. При
умножении на В [i] результат начинаем прибавлять к C[i], т. е. учитываем сдвиг
на разряд.
данном шаге результат будем накапливать в
массиве С, прибавляя к тому, что уже получили на предыдущих шагах. При
умножении на В [i] результат начинаем прибавлять к C[i], т. е. учитываем сдвиг
на разряд.
При такой организации вычислений значения элементов массива С
могут стать большими либо равными ![]() 10. Можно после получения очередного С [i]
проверять его и, если С 10, поступать так, как поступали при вычислении суммы.
Тогда количество проверок будет равно N•M. Разумнее разнос по разрядам
выполнить
10. Можно после получения очередного С [i]
проверять его и, если С 10, поступать так, как поступали при вычислении суммы.
Тогда количество проверок будет равно N•M. Разумнее разнос по разрядам
выполнить
после того, когда вычисление произведения закончено. Количество проверок будет равно количеству цифр в произведении А • В. Количество цифр произведения двух чисел не превосходит k=N+M. (Почему?)
![]() Алгоритм вычисления произведения будет следующим:
Алгоритм вычисления произведения будет следующим:

нц для i от 1 до![]()
С [Н- Ц: _С [Н- ![]() [i] div 10;
[i] div 10;
С —С [il mod 10;

кц
![]()
![]() Полученные алгоритмы сложения, вычитания,
умножения многозначных чисел можно использовать для моделирования действий над
числами в какой-либо системе счисления. Для этого необходимо помнить, что если
у нас система счисления имеет основание р, то р единиц одного разряда образуют
единицу нового разряда. Другими словами, необходимо число 10 в алгоритмах
(3.16), (3.17), (3.18) заменить основанием системы счисления.
Полученные алгоритмы сложения, вычитания,
умножения многозначных чисел можно использовать для моделирования действий над
числами в какой-либо системе счисления. Для этого необходимо помнить, что если
у нас система счисления имеет основание р, то р единиц одного разряда образуют
единицу нового разряда. Другими словами, необходимо число 10 в алгоритмах
(3.16), (3.17), (3.18) заменить основанием системы счисления.
Вопросы
для повторения ![]()
1. Как сложить два многозначных числа?
2.
Как найти
разность двух многозначных чисел? ![]()
ЗАДАЧИ ДЛЯ ПОВТОРЕНИЯ
1. Определить, является ли данное число четным. 2. Два натуральных числа называют дружественными, если каждое из них равно сумме всех делителей другого, кроме самого этого числа. Найти все пары дружественных чисел, лежащих в диапазоне от п до К.
З. Найти натуральное число из диапазона от п до К, которое имеет наибольшее количество делителей.
4. Разложить
дробь p/q на сумму дробей вида l/n. Например, при р—![]()
1
7 4 + л!.т+ 2 3l![]()
5. Найти все совершенные числа, меньшие N. Число совершенно, если оно равно сумме всех своих делителей, за исключением самого числа.
6. Любую целочисленную денежную сумму, большую
7р., можно выплатить без сдачи трешками и пятерками (докажите). Для данного п найти все такие целые неотрицательные а и Ь, что За+5Ь=п.
7. Сообщество
роботов живет по следующим за![]() конам:
конам:
![]() l) один раз в начале года они
объединя}отся в группы по З или по 5 роботов;
l) один раз в начале года они
объединя}отся в группы по З или по 5 роботов;
2) за год группа из З роботов собирает б новых, а группа из 5 роботов собирает 9 новых;
З) роботы объединяются так, чтобы собрать за год наибольшее количество роботов; каждый робот живет З года после сборки.
Известно начальное количество роботов. Все они только что собраны.
Сколько роботов будет через N лет?
8. Даны
два натуральных числа п и Ь, причем Ь ![]() нечетное число больше 1.
нечетное число больше 1.
Определить, что делает следующий ниже фрагмент программы:
нц пока ![]()
 п: div (n, 2)
п: div (n, 2)если п —0
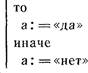
все
9. Два двузначных числа, записанных одно за другим, образуют четырехзначное число, которое делится на их произведение. Найти эти числа.
10. Найти натуральные числа из отрезка [п; К], количество делителей у которых является произведением двух простых чисејт.
11. Дано натуральное число п. Найти четверки простых чисел и меньших п, принад,лежащих одному десятку (например ll, 13, 17, 19).
![]() 12. Дано натуральное число п. Выяснить,
имеются ли среди чисел п, п + I 2п числа-близнецы, т. е. простые числа,
разность между которыми равна 2.
12. Дано натуральное число п. Выяснить,
имеются ли среди чисел п, п + I 2п числа-близнецы, т. е. простые числа,
разность между которыми равна 2.
13. Дано натуральное число п. Получить все числа, взаимнопростые с п и меньше его.
14. Дано натуральное число п. Получить все его простые делители.
15. Даны натуральные числа р и q. Получить все делители числа р, взаимнопростые с q.
16, Найти К-е простое число в арифметической прогрессии 11,
21, 31, 41, 51, 61, . Привести ответ для К— ![]() 1, 10, 100, 1000 и т.
д.
1, 10, 100, 1000 и т.
д.
17. Сократить дробь a/b (а, Ь — натуральные числа). 18. Даны 4 целых числа а, Ь, с, d. Написать программу, вычисляющую сумму обыкновенных дробей a/b+ +c/d в виде х/у.
19. дано натуральное число п. Определить количество сотен (тысяч, миллионов) в нем.
20. Ввести период дроби. Напечатать числитель и знаменатель.
21. Натуральное число из п цифр является числом Армстронга, если сумма его цифр, возведенных в п-ю степень, равна самому числу (l53= 53 +33 ). Получить все числа Армстронга для п = 2, З, 4.
22, Дано натуральное число п. Чему равна сумма его цифр?
![]() 23. Дано натуральное число п. Верно ли,
что сумма цифр этого числа является нечетной?
23. Дано натуральное число п. Верно ли,
что сумма цифр этого числа является нечетной?
![]() 24. Дано натуральное число п. Верно ли,
что это число содержит ровно три одинаковые цифры? Если да, то укажите эти
цифры.
24. Дано натуральное число п. Верно ли,
что это число содержит ровно три одинаковые цифры? Если да, то укажите эти
цифры.
![]() 25. Посчитать сумму цифр всех целых чисел
от I до N.
25. Посчитать сумму цифр всех целых чисел
от I до N.
26. Дано натуральное число п. Выбросить из записи числа п все цифры, равные 1, оставив при эа•ом прежним порядок остальных цифр. Например, из 5101234 50234.
27. Из записи натурального числа выбросить цифры I и 5, оставив прежним порядок цифр. Например, число 527012 преобразуется в число 2702.
28. Найти . такие две различные наименьшие степени натурального числа п, у которых три последние цифры одинаковы.
29. Дано натуральное число п. Выбросить из записи числа все четные цифры.
30. Дано натуральное число п. Определить, является ли оно палиндромом (читается одинаково с начала и с конца).
31. Найти все числа из диапазона от п до т, которые при возведении в квадрат дают палиндром.
32. Найти все числа-палиндромы из диапазона от п до т, которые при возведении в квадрат также дают палиндромы.
33. Найти остаток от деления числа, записываемого с помощью К семерок, на число а, К и а— заданные натуральные числа.
34. Все натуральные числа выписаны подряд, начиная с единицы. Определить, какая цифра стоит на N-M месте.
35. На
интервале (1000; 9999) найти все простые числа, каждое из которых обладает тем
свойством, что сумма первой и второй цифр записи этого числа равна сумме
третьей и четвертой. ![]()
36. Высадившись
на планете Альфа, населенной разумными «осьминогами>>, космонавты
увидели. написанную на стене близлежащего строения формулу 99 •99= ![]() =
1210. Сколько щупальцев было у населявших планету Альфа «осьминогов»?
=
1210. Сколько щупальцев было у населявших планету Альфа «осьминогов»?
37. Среди простых чисел, не превосходящих N, найти такое, в двоичной записи которого максимальное число единиц.
38. Найти двоичное представление для чисел Ферма, которые представимы в виде 22 + 1.
39. Задана последовательность длины N, состоящая из единиц и нулей. Определить количество М-значных двоичных чисел (М М), входящих в указанную последовательность, которые делятся на 21.
40. Напечатать шестнадцатеричную таблицу умножения так же, как печатают обычную на обложке тетради.
41. Десятичная дробь определяется следующим образом:
![]() ] abc...d [.e/g...h],
] abc...d [.e/g...h],
где а, Ь, с![]() h — десятичные цифры
от 0 до 9, элементы в квадратных скобках не являются обязательными. Найти
корень уравнения Х/А=В (А и В — десятичные дроби), представив его в виде
десятичной дроби, сохранив все ее десятичные знаки.
h — десятичные цифры
от 0 до 9, элементы в квадратных скобках не являются обязательными. Найти
корень уравнения Х/А=В (А и В — десятичные дроби), представив его в виде
десятичной дроби, сохранив все ее десятичные знаки.
42. Написать программу, которая вычисляет значение выражения.
![]()
Ответ представить в виде несократимой дроби p/q, где р и q — натуральные числа.
43. дана последовательность
![]()
Составить программу, в которой используются только целые
числа, для печати члена последовательности в виде обыкновенной дроби. Например:
![]() при
должно быть напечатано 19/10, при М —4 должно быть напечатано 651/290.
при
должно быть напечатано 19/10, при М —4 должно быть напечатано 651/290.
44. Вывести на экран картинку, изображающую умножение <<столбиком» двух заданных целых чисел.
![]() 45. Написать программу, которая выводит
картинку, изображающую умножение «столбиком» двух данных чисел.
45. Написать программу, которая выводит
картинку, изображающую умножение «столбиком» двух данных чисел.
Например, сомножители: 398.56, 85.03.![]()
147
39856 х
8503 l9568
+ 199280
318848
![]()
338895568
Произведение: 33889.5568.
46. Определить количество повторений каждой из цифр 0, l, 2, 9 в числе NN, 1000.
47. Найти частное от деления a/b с точностью цифр после запятой. Числа а и Ь вводятся с не более чем 200 цифрами.
48. Даны две таблицы: М1, М![]()
Каждый элемент либо одна из цифр 0, 1, 9, либо десятичная точка (она появляется не более одного раза). Написать алгоритм сравнения «записанных» в таблицу величин. Например:
|
|
|
|
|
|
|
|
|
|
|
|
|
м |
З |
4 |
|
|
7 |
4 |
9 |
О |
О |
О |
|
|
о |
о |
0 |
|
|
|
О |
з |
4 |
2 |
Результат: «М так
как 341.749<342. ![]()
49. Даны целые числа т и
п ![]() указывающие момент времени т часов п
минут. Определить наименьшее время (число полных минут), которое должно пройти
до того момента, когда часовая и минутная стрелки на циферблате совпадут; расположатся
перпендикулярно друг другу.
указывающие момент времени т часов п
минут. Определить наименьшее время (число полных минут), которое должно пройти
до того момента, когда часовая и минутная стрелки на циферблате совпадут; расположатся
перпендикулярно друг другу.
50. Даны п положительных
чисел А 1, 142, Ап И Т положительных чисел Щ, В Вт. Сумма всех Ai равна сумме
всех Щ. Доказать, что можно построить (и описать как) массив C[i, Л; ![]() который
удовлетворяет следующим требованиям:
который
удовлетворяет следующим требованиям:
1) все (i, ј) неотрицательные числа;
2) в массиве по крайней мере (т— 1) нулей; З) сумма каждой строки равна А;
4) сумма каждого ј-го столбца равна В].
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ
1. Число задано своим двоичным представлением (длина числа не превышает 10 000 двоичных разрядов). Необходимо определить, делится ли число на 15.
2. а) Как-то раз в аптеку доставили 10 флаконов по 1000 пилюль. Не успел провизор расставить флаконы на полке, как почтальон принес телеграмму, в которой было следующее:
![]() «Воздержаться от
продажи лекарства. По ошибке фармацевта в одном из флаконов каждая пилюля
содержит на 1 мг лекарства больше допустимой дозы. Просьба незамедл ительно
вернуть флакон с повышенной дозой лекарства».
«Воздержаться от
продажи лекарства. По ошибке фармацевта в одном из флаконов каждая пилюля
содержит на 1 мг лекарства больше допустимой дозы. Просьба незамедл ительно
вернуть флакон с повышенной дозой лекарства».
Сколько взвешиваний придется сделать провизору для определения флакона с повышенной дозой лекарства, если масса пилюли с допустимой дозой лекарства равна 10 мг?
б) Через какое-то время в аптеку доставили еще 10 флаконов того же лекарства. И на этот раз не успели распаковать коробку с флаконами, как почтальон принес телеграмму с извещением о том, что на этот раз фармацевт допустил более серьезную ошибку. В посылке могли оказаться от 1 до 10 флаконов с пилюлями, каждый из которых на мг тяжелее нормы.
Сколько взвешиваний придется сделать провизору в этот раз для определения флаконов с повышенной дозой лекарства?
З, Предположим, что у нас есть весы с двумя чашами и по одной
штуке гирь 1, З, 9, 27, ![]() Уравновесить груз массой М на весах.
Уравновесить груз массой М на весах.
149
4. Сосчитать количество единиц в двоичной записи числа i, заданного в десятичной системе счисления.
5. Последовательность 011212201220200112... строится следующим образом. Сначала пишется 0, затем повторяется следующее действие: уже написанную часть приписывают справа с заменой О на 1, 1 на 2, 2 на 01 т. е.
![]() 220 .
220 .
Составить алгоритм, который по введенному N (00<2000000000) определяет, какое число стоит на N-M месте в последовательности.
![]() 6. Даны массивы Х [1..100] и Y[l..100].
Записать алгоритм, последовательно меняющий местами значения элементов Х [К] и
У [К], 1, 2 100, не используя промежуточных переменных.
6. Даны массивы Х [1..100] и Y[l..100].
Записать алгоритм, последовательно меняющий местами значения элементов Х [К] и
У [К], 1, 2 100, не используя промежуточных переменных.
7. Точки с целочисленными координатами из 1-го квадранта
помечаются числами из множества (0,![]()
Очередная точка помечается в том случае, если все точки ниже и левее ее уже помечены. При этом точке приписывается минимальное число, отсутствующее в вертикали и горизонтали, проходящей через точку. Первой помечается точка (О; 0),
Написать программу, которая: 1) по заданным
координатам х и д, х д>О, х, у ![]() целые, определяет пометку точки;
целые, определяет пометку точки;
2) по заданным координате х и пометке точки К (х К>О, х, К — целые) определяет вторую координату точки.
![]() 8. Найти длину периода и сам период дроби
в Р-ичной системе счисления, представляющей рациональное число N/M (для
конечных дробей считать, что длина
8. Найти длину периода и сам период дроби
в Р-ичной системе счисления, представляющей рациональное число N/M (для
конечных дробей считать, что длина ![]() периода равна 1). М, М, Р— целые
десятичные числа,
периода равна 1). М, М, Р— целые
десятичные числа,
![]()
9. Для введенных действительного числа и натурального числа
необходимо найти наилучшее при![]() ближение r в виде рациональной дроби p/q,
где q<qтах• 10. Пусть запись числа А в позиционных системах счисления с
основанием р и q имеет вид бесконечной периодической дроби с периодом 2:
ближение r в виде рациональной дроби p/q,
где q<qтах• 10. Пусть запись числа А в позиционных системах счисления с
основанием р и q имеет вид бесконечной периодической дроби с периодом 2:![]()
А —0, ![]() (ba)q,
(ba)q,
где a+b.
Написать программу, которая для введенных натуральных чисел р и q (2<р, q<30, p>q) находит и выводит все возможные пары значений цифр а и Ь, удовлетворяющих соотношению (*). Если таковых нет, вывести сообщение «Пригодных цифр нет».
Примеч ан и е. Значением числа, запись которого в
позиционной системе счисления с основанием S есть 0, cdef (где с, d, е, —
цифры), является![]()
11. Определим множества КЕ рекуррентно. Пусть
![]() 1]. Разделим отрезок [0, Ц на три части
точками 1/3 и 2/3 и удалим из него интервал (1/3, 2/3). Получим множество Щ,
состоящее из двух оставшихся отрезков [0, 1/31 и [2/3, Ц. Каждый из них
разделим на три части
1]. Разделим отрезок [0, Ц на три части
точками 1/3 и 2/3 и удалим из него интервал (1/3, 2/3). Получим множество Щ,
состоящее из двух оставшихся отрезков [0, 1/31 и [2/3, Ц. Каждый из них
разделим на три части
(точками 1/9 и 2/9 для первого отрезка и точками
7/9 и 8/9 — для второго) и удалим средние
интервалы (1/9, 2/9) и (7/9, 8/9). Таким образом, получаем множество К2 и т. д.
Пусть мы построим множество ki. Поделим каждый оставшийся отрезок из ki на З
части и удалим из этих сегментов средние интервалы. Получим, таким образом, из
Щ множество ki+l![]()
Вводятся З целых числа п, а, Ь. Необходимо определить, принадлежит ли точка с координатой a/b множеству кп.
12. Число называется совершенным, если оно равно сумме всех своих делителей, за исключением его самого. Любое четное совершенное число представимо в виде 2P - l (2Р— 1), где р — простое число.
Найти двоичное представление для максимального совершенного четного числа меньше введенного М.
![]() 13. Заданы натуральные числа е, К, т, t в
записи химической реакции ХеАк+У—» YmAi+X, где А, Х, У — атомы или группы
атомов. Написать алгоритм для прохождения таких натуральных коэффициентов, при
которых стрелку можно было бы заменить знаком равенства.
13. Заданы натуральные числа е, К, т, t в
записи химической реакции ХеАк+У—» YmAi+X, где А, Х, У — атомы или группы
атомов. Написать алгоритм для прохождения таких натуральных коэффициентов, при
которых стрелку можно было бы заменить знаком равенства.
14. Вводятся целые числа а и Ь. Пусть у треугольника АВС координаты вершин А (О; 0), В (а; Ь), а обе координаты С (х; у) целые числа, и площадь треугольника АВС не равна нулю. Какую минимальную площадь может иметь треугольник АВС?
15. Имеется
N банок с целочисленными объемами И, ![]() Vn литров, пустой сосуд и кран с водой.
Можно ли с помощью этих банок налить в сосуд ровно V литров воды?
Vn литров, пустой сосуд и кран с водой.
Можно ли с помощью этих банок налить в сосуд ровно V литров воды?
16. Вычислить число е (основание натурального логарифма) с точностью п значащих десятичных цифр после запятой. Можно использовать числовой ряд
![]()
17. Вывести
на экран число 2't , ![]() [О ООО, п нату
[О ООО, п нату![]() ральное.
ральное.
18. Вводится М. Необходимо найти, на сколько нулей оканчивается •N.
19. Вводятся
два числа и Р. Найти такое максимальное число М, что N! делится на Р и ,
но не делится Н а РИА- 1![]()
Примеч а н ия. 1. Числа N и Р так велика, что нет смысла считать значение N!.
2. Числа N и Р— натуральные.
20. Натуральное число представить в виде суммы натуральных слагаемых так, чтобы их произведение было максимальным.
21. Задается
любое положительное действительное число R. Найти положительные действительные
R 1, R2, ![]() п, такие, что R = R 1 • 122
п, такие, что R = R 1 • 122![]()
[52
22. Вывести в порядке возрастания все обыкновенные несократимые дроби, заключенные между 0 и l , знаменатели которых не превышают 15. Массив при этом заводить не следует.
23. Дан
многогранник, в вершинах которого записаны целые числа. Одним ходом можно
выбрать одно ребро, и к числу, записанному в одном из его концов, прибавить 1,
а из числа, записанного в другом конце, ![]() вычесть 1.
вычесть 1.
Какому необходимому и достаточному условию должны удовлетворять записанные числа, чтобы с помощью таких ходов можно было добиться, чтобы во всех вершинах был одновременно записан нуль? Ответ обосновать.
24. В нулевой момент времени мастеру одновременно поступает N работ. Работы пронумерованы от 1 до М.
![]()
![]()
![]()
![]()
![]()
![]()
![]() Для
каждой работы i заранее известно следующее: К ) время выполнения работы ti,
кратное суткам;
Для
каждой работы i заранее известно следующее: К ) время выполнения работы ti,
кратное суткам;
2) штраф с; за ка»кдые сутки ожидания работы i до момента начала ее выполнения.
Одновременно может выполняться только одна работа, и если мастер приступает к выполнению некоторой работы, то он продолжает выполнять ее, пока не закончит. Суммарный штраф, который надо будет уплатить, выражается следующим образом:
сумма ![]() начала выполнения
работы i) по всем г.
начала выполнения
работы i) по всем г.
Найти такой порядок выполнения работ, чтобы штраф оказался минимальным.
25. В ряд лежат N арбузов, пронумерованных
от ![]() до М. Нам известно, что:
до М. Нам известно, что:
1) массы первого и арбузов tnl и тм соответствен но;
2) масса арбуза есть среднее арифметическое масс двух соседних арбузов, увеличенное на d:
![]()
![]() По введенным Tl, тм, N, d и ј найти тј.
Ограничение:
По введенным Tl, тм, N, d и ј найти тј.
Ограничение: ![]() N 200.
N 200.
Необходимо в рамках формулировки задачи предусмотреть проверку корректности данных программы. ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Натуральное число, записанное в десятичной системе
счисления, называется сверхпростым, если оно остается простым при любой перестановке
своих цифр. Определить, является ли данное число сверхпростым. 2.
Последовательность, состоящую из четырех целых чисел а, Ь, с, d, одним ходом
можно преобразовать в последовательность la—bl, lb—cl,![]()
Доказать, что какой бы ни была начальная последовательность, многократным повторением ходов можно получить последовательность, состоящую из четырех нулей.
З. Дано целое неотрицательное число К, не превышающее миллиона. Напечатать фразу «К ворон» русскими словами. (Например, если К = 23, то должно быть напечатано «двадцать три вороны», если К—1, то — «одна ворона». )
4. Написать программу, переводящую заданную сумму в рублях (до 30 000 тысяч включительно) в ее полное название. (Например:
СУММА? 29320,25 — ДВАДЦАТЬ ДЕВЯТЬ ТЫСЯЧ ТРИСТА ДВАДЦАТЬ РУБЛЕЙ ДВАДЦАТЬ ПЯТЬ
КОПЕЕК
Сокращать слова нельзя.
5.
Написать
программу, которая выдаст словами название введенного действительного числа.
(Например: 25.23 — двадцать пять целых двадцать три сотых.)![]()
![]() 6. Число является палиндромом, если оно
читается одинаково слева направо и справа налево. Рассмотрим некоторое
натуральное число N. Если это число не палиндром, то изменим порядок его цифр
на обратный и сложим исходное число с получившимся. Если сумма
6. Число является палиндромом, если оно
читается одинаково слева направо и справа налево. Рассмотрим некоторое
натуральное число N. Если это число не палиндром, то изменим порядок его цифр
на обратный и сложим исходное число с получившимся. Если сумма
![]()
не палиндром, то над ней повторяем то же действие и т. д., пока не получится палиндром. До настоящего времени неизвестно, завершается ли этот процесс для любого натурального N.
![]() Даны натуральные числа К, L, М (k<L). Проверить, верно
ли, что для любого натурального числа из диапазона от К до L процесс
завершается не позднее, чем после М таких действий. Если нет, то выдать числа,
для которых процесс не завершился, и количество таких чисел.
Даны натуральные числа К, L, М (k<L). Проверить, верно
ли, что для любого натурального числа из диапазона от К до L процесс
завершается не позднее, чем после М таких действий. Если нет, то выдать числа,
для которых процесс не завершился, и количество таких чисел.
7. Все квадраты натуральных чисел выписаны подряд, начиная с единицы. Определить, какая цифра стоит на N-M месте.
8. Доказать, что в 16-разрядной ЭВМ с объемом ОЗУ 192 Кбайт в любой момент времени t существуют две ячейки, содержащие одинаковые числа.
9. Римские числа.
б) Записать данное целое число из диапазона от до 1999 римскими цифрами.
![]() в) Перевести число, записанное римскими
цифрами, в десятичную систему счисления.
в) Перевести число, записанное римскими
цифрами, в десятичную систему счисления.
10. ![]() Можно ли
разбить все натуральные числа 1, 2, З,
Можно ли
разбить все натуральные числа 1, 2, З, ![]() на две такие
возрастающие последовательности Щ, Щ, аз, и bl, 62, 63, . . . , что
на две такие
возрастающие последовательности Щ, Щ, аз, и bl, 62, 63, . . . , что ![]() для
любого К— 1,
для
любого К— 1, ![]() По введенному числу N определить, какому
номеру оно соответствует и какое число будет с ним в паре (не выписывая все
предыдущие ак и Ьк).
По введенному числу N определить, какому
номеру оно соответствует и какое число будет с ним в паре (не выписывая все
предыдущие ак и Ьк).
11. Послание от внеземной
цивилизации представляет собой набор из N символов, каждый из которых является
нулем или единицей. Число N является произведением двух простых чисел и ученые
предполагают, ![]() что эта строка — закодированная
прямоугольная «картинка», размеры которой — множители числа М.
что эта строка — закодированная
прямоугольная «картинка», размеры которой — множители числа М.
Составить программу, которая производит перекоди![]() ровку
послания и печатает картинки, заменяя каждый нуль пробелом, а единицу —
звездочкой.
ровку
послания и печатает картинки, заменяя каждый нуль пробелом, а единицу —
звездочкой.
Пример:
![]() 55
55
Послание:
![]()
lOOlOOOlOlll
12. Числа 46816M и
160l25N представлены в разных системах счисления с неизвестными основаниями ЛК ![]() и
10. Существуют ли такие М и N, что эти числа равны?
и
10. Существуют ли такие М и N, что эти числа равны?
13. Рассмотрим числовую
последовательность, определенную следующим образом: аш ![]() если i>l.
если i>l.
Вычислить все цифры перед запятой члена.
14. Написать алгоритм, который для вещественного числа х находит сумму хк к, где К = 1, 2 128, используя не более 258 умножений и 256 сложений, учитывая операции организации цикла (возведение в степень не использовать).
15. Составить программу, которая выполняет сложение двух пятиразрядных двоичных чисел, пользуясь операциями «И», «ИЛИ», «НЕ» и «СДВИГ ВЛЕВО» (на один разряд), которые выполняются так:
1) С== А ; переменной С присваивается значение числа А, в котором нули заменяются на 1, а единицы — на 0 (Операция «НЕ»).
2) МВ — поразрядная операция, результат вы: полнения которой определяется таблицей (Операция <<ИЛИ>>).
ТАБЛИЦА ![]() ovo=o
ovo=o
![]()
З) С = АЛВ — поразрядная операция, результат выполнения которой определяется таблицей 2 (Операция «И»).
ТАБЛИЦА 2 оло=о
![]()
4) ![]() — поразрядный сдвиг
влево, т. е. раз
— поразрядный сдвиг
влево, т. е. раз![]() ряд С получает значение (Н- 1)-го разряда
числа
ряд С получает значение (Н- 1)-го разряда
числа ![]() А, 5-й (младший) разряд С становится
равным 0. Каждое из исходных чисел меньше 10 0002.
А, 5-й (младший) разряд С становится
равным 0. Каждое из исходных чисел меньше 10 0002.
16. Для заданного К найти такое N, что в десятичном числе 2 N встретится К нулей подряд.
17. По заданному п составить программу вычисления
![]()
Оценить, для каких достаточно больших п будет работать эта программа.
18. Составить программу, которая в полной записи числа 77! (77 факториал) укажет в порядке убывания номера разрядов, содержащих цифру 7.
П р и м е ч а н и е. Разряды числа нумеруютс.я в следующем порядке:
разряд единиц имеет номер 1, десятков —2, сотен —![]()
19. Из
заданного натурального числа вычеркнуть ![]() цифр так, чтобы
полученное число было возможно большим.
цифр так, чтобы
полученное число было возможно большим.
20. Найти
все десятичные цифры числа 100! — 2 100 ![]() 21. На правильно
идущих часах с 12-часовым циферблатом имеются часовая, минутная и секундная
стрелки, движущиеся плавно (без скачков).
21. На правильно
идущих часах с 12-часовым циферблатом имеются часовая, минутная и секундная
стрелки, движущиеся плавно (без скачков).
В какое время все стрелки образуют между собой углы 120 0 ? Как долго за сутки углы, образованные между всеми стрелками, одновременно будут в пределах от 119 0 до 121 0 ?
22. Задана таблица чисел. Алгоритм на каждом шаге выбирает в этой таблице строку (или столбец), сумма элементов которой меньше нуля, и умножает все эти элементы на (—1).
Доказать, что алгоритм не может работать бесконечно долго.
![]() 23. Дано натуральное число п, являющееся
квадратом некоторого другого натурального числа.
23. Дано натуральное число п, являющееся
квадратом некоторого другого натурального числа.
Составить программу, которая вычисляет п используя только операции сложения и вычитания.
24. Найти значение функции Р (1990), вычисляемой по следующему алгоритму:
![]()
![]()
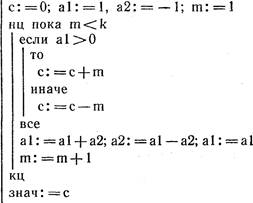 —а2;
—а2;
кон
Придумать алгоритм для вычисления этой функции, „в записи которого не используются команды ветвления и цикла.
25. Вычислить
значение функции ![]() где т — число знаков, содержащихся в
десятичной записи числа п!
где т — число знаков, содержащихся в
десятичной записи числа п!
![]() 26. Известно, что для любых натуральных
чисел а и Ь существуют такие целые числа и и v, что справедлива формула:
аи+Ьо=НОД (а, Ь). По введенным а и Ь найти какие-нибудь и и о.
26. Известно, что для любых натуральных
чисел а и Ь существуют такие целые числа и и v, что справедлива формула:
аи+Ьо=НОД (а, Ь). По введенным а и Ь найти какие-нибудь и и о.![]()
![]() 27. В круге стоит человек, пронумерованных
по порядку от до М. При расчете на первый-второй, начиная с первого человека,
каждый второй выходит из круга, до тех пор, пока не останется один человек.
27. В круге стоит человек, пронумерованных
по порядку от до М. При расчете на первый-второй, начиная с первого человека,
каждый второй выходит из круга, до тех пор, пока не останется один человек.
![]() Доказать, что его номер можно найти
следующим образом: представить N в двоичной системе счисления, затем поставить
крайний левый единичный бит числа после самого правого разряда числа.
Доказать, что его номер можно найти
следующим образом: представить N в двоичной системе счисления, затем поставить
крайний левый единичный бит числа после самого правого разряда числа.
![]() Например:
Например: ![]() 11002, номер
последнего человека 10012=9.
11002, номер
последнего человека 10012=9.
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ПОВЫШЕННОЙ СЛОЖНОСТИ
1. Вспомним, что признаком деления на 9 в десятичной системе счисления является делимость на 9 суммы цифр числа. Действительно, пусть есть число
![]()
тогда
S ET10d 9 ![]() ) + а п
) + а п![]()
А так как l0h — l делится
на 9 нацело, то и S 9 ![]() mod 9.
mod 9.
Аналогично получаем, что признаком деления на 15 в системе счисления с основанием 16 будет делимость на 15 суммы всех шестнадцатеричных цифр числа.
Разбиваем двоичное число справа налево на тетрады, которые
однозначно можно преобразовать в шестнадцатеричные цифры, находим их сумму и
делим ее на 15. Если остаток О, то введенное число делится на 15, иначе — не
делится.![]()
2. а) Для решения задачи не нужно взвешивать пилюли из каждого флакона, т. е. производить 10 взвешиваний. Достаточно одного взвешивания для определения флакона с повышенной дозой лекарства.
Для этого необходимо взять 1 пилюлю из первого, 2 пилюли из второго, З пилюли из третьего 10 пилюль из десятого флакона. Затем следует положить 55 отобранных пилюль на одну чашу весов и взвесить их. Если бы все пилюли были с допустимой дозой лекарства, их масса составила бы 550 мг. Предположим, что пилюјш весили 551 мг, или на 1 мг больше, чем следует. Это значит, что имеется ровно одна пилюля с повышенной дозой лекарства, а ровно одна пилюля была извлечена из первого флакона. Если бы масса 65 пилюль оказалась на З мг больше нормы, то это означало бы, что среди отобранных пилюль имеются З пилюли с повышенной дозой лекарства. Их можно было извлечь только из третьего флакона. Таким образом количество взвешиваний можно понизить до 1.
б) Метод решения, позволивший за одно взвешивание определить флакон, содержащий лекарства с повышенной дозой, в данном случае не применим, однако его можно модифицировать.
Для того чтобы решить задачу, необходимо воспользоваться последовательностью, которая бы сопоставляла каждому флакону отличный от других номер и обладала бы е:це одним дополнительным свойством: сумма членов любой ее подпоследовательности должна быть оз•личноЙ от суммы членов любой другой ее подпоследовательности. Примером такой последовательности может служить следующая: 1, 2, 4, 8, все члены ее — степени числа 2. Эта последовательность лежит в основе двоичной системы счисления.
Решение задачи состоит в том, чтобы взять пилюлю из первого закона, 2 пилюли из второго, 4 пилюли из третьего и т. д., затем собрать все отобранные пилюли и взвесить. Предположим, что пилюли оказались на 27 мг тяжелее, чем нужно. Так как каждая пилюля с повышенной дозой лекарства тяжелее нормальной на
I мс, то, разделив 27 на 1, мы получим 27 число более тяжелых пилюль.
Запишем число 27 в двоичной системе: 11011. Двоичные разряды, в которых стоят единицы, говорят нам, какие степени числа 2 в сумме дают двоичное число 11011 (или десятичное число 27): 1, 2, 8, 16. Единицы стоят в первом, втором, четвертом и пятом двоичных разрядах. Следовательно, непригодные пилюли с повышенным содержанием лекарства находятся в первом, втором, четвертом и пятом флаконах.
![]() З. При представлении числа в троичной
системе счисления обычно используются цифры (), I и 2. Однако можно
использовать цифры 1, 0 и — 1. Для получения такой записи поступим следующим
образом: будем переводить М в троичную систему счисления, и каждый раз, когда
при делении на З будет получаться 2, будем увеличивать частное на 1, а в
остатке писать (— l). Например:
З. При представлении числа в троичной
системе счисления обычно используются цифры (), I и 2. Однако можно
использовать цифры 1, 0 и — 1. Для получения такой записи поступим следующим
образом: будем переводить М в троичную систему счисления, и каждый раз, когда
при делении на З будет получаться 2, будем увеличивать частное на 1, а в
остатке писать (— l). Например: ![]() — 1 • 33-4-0-32— l +0- 30.
— 1 • 33-4-0-32— l +0- 30.
Груз V положим на первую чашу весов. Г'рузы с коэффициентом в разложении — поставим на эту же чашу, а грузы с коэффициентом — на другую.
Объясните, почему данный алгоритм работает.
Опишите процесс уравновешивания груза неизвестной массы на чашечных весах, используя ту же систему гирь.
4. Алгоритм:
|
cnt : |
{cnt — счетчик е,циниц в i.} |
|
while |
[цикл повторяется число раз,} |
|
begin |
{равное числу единиц в ij |
|
|
{«Убираем» крайнюю справа} |
|
cnt: — |
{единицу в двоичной записи) |
|
end; |
{числа.} |
![]()
100![]() and (i— 1)
and (i— 1)
6 Информатика, 8—9 кл. i61
5. Пусть А 4— К-й член последовательности. Рассмотрим
последовательность, формируемую по следующему правилу: ао=0; фрагмент ![]() получаем
приписыванием к фрагменту ао...а справа аналогичного фрагмента, в котором
каждый член увеличен на единицу. ПОЛУЧаеМ О
получаем
приписыванием к фрагменту ао...а справа аналогичного фрагмента, в котором
каждый член увеличен на единицу. ПОЛУЧаеМ О ![]() .
.
![]() Докажем, что ак есть сумма единиц в
двоичном представлении числа К. Доказательство проведем по индукции. Для ао=0
это справедливо. Пусть предположение справедливо для всех щ,
Докажем, что ак есть сумма единиц в
двоичном представлении числа К. Доказательство проведем по индукции. Для ао=0
это справедливо. Пусть предположение справедливо для всех щ, ![]() всех чисел
i, состоящих из не более чем (К— 1) двоичных разрядов). Тогда в двоичном
разложении числа l,
всех чисел
i, состоящих из не более чем (К— 1) двоичных разрядов). Тогда в двоичном
разложении числа l, ![]() в К-м разряде появляется добавочная
единица, и поэтому а— 1-Fat—2h— 1.
в К-м разряде появляется добавочная
единица, и поэтому а— 1-Fat—2h— 1.
Возьмем ai mod З и получим число, стоящее на i-M месте в последовательности, описанной в условии задачи.
Для того чтобы найти а;, необходимо по доказанному сосчитать количество единиц в двоичной записи числа i (см. задачу 4).
![]() 60 Будем менять местами содержимое
переменных А и В. Существует несколько способов сделать это.
60 Будем менять местами содержимое
переменных А и В. Существует несколько способов сделать это.
 В
В
2) Можно использовать логическую операцию XOR (исключающее ИЛИ). Таблица истинности для XOR следующая:
![]() XOR l XORO=l 0 XOR
OXOR
XOR l XORO=l 0 XOR
OXOR![]()
Операция XOR над двумя переменными в машине реализуется как
побитовая операция над двоичным представлением чисел. Поэтому, в частности, А
XOR А ![]() А XOR XORA, А XOR 0=А.
А XOR XORA, А XOR 0=А.
![]()
![]() Оператор
Оператор![]() Значение в А Значение в В
Значение в А Значение в В
![]() А XORB
А XORB ![]() А XOR В
А XOR В ![]()
![]() XOR
В А XOR В (А XOR В) XOR В
XOR
В А XOR В (А XOR В) XOR В![]()
—А XOR (В XOR В)![]()
![]() А XOR
А XOR![]()
![]() XORB (А XOR В) XORA
XORB (А XOR В) XORA ![]()
![]() — В
XOR (А
— В
XOR (А![]()
7. Если рассмотреть битовые представления числа А [i, Л, помечающего точку (i, ј), и чисел i и ј, то обнаруживается, что А [i, XOR f, откуда получается, что А р, Л XOR i=j, А [i, Л XOR j=i.
Покажем, что А [i, XOR ј.
1) Число А [i, XORj не встречалось еще ни в строке i, ни в столбце ј. От противного: существует такое (, что
![]() XOR
XOR XOR
XOR
XOR XOR ![]()
![]() i XOR XOR
i XOR XOR![]()
2)
Пусть существует такое XOR ј, что К = ![]() XOR XORM, и
К еще не встречалось в строке i и столбце (напомним, что по предположению все
XOR XORM, и
К еще не встречалось в строке i и столбце (напомним, что по предположению все ![]() остальные
уже заполненные элементы равны i XOR ј, поэтому и МЯ).
остальные
уже заполненные элементы равны i XOR ј, поэтому и МЯ).
Тогда, так как M>i, то существует бит с номером t такой,
что для любого биты Мг и ir равны, ![]() бит М— 1, it=O. Но так как
бит М— 1, it=O. Но так как
![]() XOR ХО? Е,
то 1.
XOR ХО? Е,
то 1.
![]() Так как и LXORi=jXORM, то L
Так как и LXORi=jXORM, то L ![]() = jXORM XORi. Рассмотрим iXORM. В
силу вышесказанного для любого бита с номером R, R>t,
= jXORM XORi. Рассмотрим iXORM. В
силу вышесказанного для любого бита с номером R, R>t,
(i
XOR а![]()
При
этом 1, следовательно![]()
(Е XOR для
![]() и
и
(iXORjXOR для r=t,
т. е. L<j?! Получили противоречие.
![]()
8. Введем переменную N1=N. Пусть Nl и М заданы в десятичной системе счисления. Переведем дробь Л4}/М в систему счисления с основанием р.
Пусть в системе с основанием р искомая дробь 0, ща2... . Получаем:
![]()
Умножим правую и левую части равенства на
р:![]()
+ arp ¯l -К- N1 .р/М. Выделяя целую часть выражений слева и справа от знака равенства, получаем: есть целая часть от (N1•p/M). Обозначим • р mod М; очевидным образом получаем аур¯ + =N2/M. Домножая на р и находя целую часть, опять же имеем: а2 есть целая часть от (N2.p/M); продолжая аналогично, определяем коэффициенты аз, и т. д.
В ходе выделения цифр a.i мы можем получить различных значений Ni не более чем М (по приведенному алгоритму выше у нас всегда Ni<M).
Если вдруг какие-то два остатка совпадают: ![]() i+j, то
совпадают и цифры разложения: aj+l, а
i+j, то
совпадают и цифры разложения: aj+l, а![]() т. е. цифры (щ +1, ај) образуют один ИЗ
кратных периодов. Нам надо найти минимальную длину такой периодически
повторяющейся последовательности, которая равна количеству цифр между двумя
ближайшими повторяющимися остатками, и сами цифры.
т. е. цифры (щ +1, ај) образуют один ИЗ
кратных периодов. Нам надо найти минимальную длину такой периодически
повторяющейся последовательности, которая равна количеству цифр между двумя
ближайшими повторяющимися остатками, и сами цифры.
Поступаем следующим образом. Выделяем М цифр р-ичной дроби
(исходя из вышесказанного, к этому моменту период уже обязан начаться).
Запот;инаем ![]() и ищем первый такой остаток Nk, К>т,
что Nm=Nk. Величина как раз и есть искомая длина периода.
и ищем первый такой остаток Nk, К>т,
что Nm=Nk. Величина как раз и есть искомая длина периода.
9. Обозначим: р — числитель, а q знаменатель искомой дроби. Вначале р— 0; 1. Если p/q меньше г, то увеличим числитель, если p/q меньше искомой дроби, то увеличим знаменатель. Если p/q=r, то решение найдено. Если тар то из всех полученных дробей выбираем ту, которая ближе всех к r.
![]() Фрагмент программы:
Фрагмент программы:
write ('r,qmax![]()
![]() ==0;q: — l;min
==0;q: — l;min![]()
REPEAT
IF p/q<r THEN р: p+l ELSE q: — ![]() d: abs(r — p/q); iF
d<min THEN
d: abs(r — p/q); iF
d<min THEN
BEGlN min: d;writeln(p![]()
END
UNTIL ![]()
10. Так как q<p, то цифры а и Ь должны лежать в пределах от 0 до ч 1. Распишем А в системе с основанием р:
д = Д + Ь2+-дг+Д+...![]()
{находим сумму бесконечно убывающей геометрической прогрессии со знаменателем р 2}
![]() 2
2
==(ар + Ь)
Аналогично для А в системе с основанием q выполняется равенство bq+a
![]()
![]() Получаем
Получаем
![]()
Вычисляем выражения в квадратных скобках, обозначив их соответственно и и о: аи = bv.
Находим НОД (и, обозначим r—u/s, = v/s.
Получаем bf, r и взаимно простые числа, следовательно,
решениями этого равенства будут числа а=ћ, b=rh, К—1, 2,![]()
при этом мы берем только те а и Ь, для которых одновременно выполняется a*b, a<-q, b<q. Для нахождения НОД используется алгоритм (3.8).
Рассмотрим другой метод решения этой задачи. Так как мы постоянно дол>кны делить отрезки на три части, то это наталкивает на мысль использовать троичную систему счисления и троичные дроби.
В первый из удаленных интервалов (1/3, 2/3) попадают только
те точки х=О, ща„аз..., в троичном разложении которых щ = 1, кроме точки 1/3=0,
1000... ![]() правого конца отрезка [О, 1/3]. Таким
образом, в Щ остаются все те точки, у которых 1, либо щ = 1, а2 аз— ...=0.
Аналогично, в множестве Щ, i>0, содержатся точки, у которых ни одно из чисел
ај, I не равно 1, а также точки, удовлетворяющие условию:
правого конца отрезка [О, 1/3]. Таким
образом, в Щ остаются все те точки, у которых 1, либо щ = 1, а2 аз— ...=0.
Аналогично, в множестве Щ, i>0, содержатся точки, у которых ни одно из чисел
ај, I не равно 1, а также точки, удовлетворяющие условию:![]()
= 1, / — фиксировано, ![]() 1, l<j,
и для любого (т. е. в записи троичной дроби только одна позиция равна 1, после
нее все остальные позиции нулевые. Эти дроби соответствуют правым концам
отрезков из множества кг).
1, l<j,
и для любого (т. е. в записи троичной дроби только одна позиция равна 1, после
нее все остальные позиции нулевые. Эти дроби соответствуют правым концам
отрезков из множества кг).
Запись алгоритма на языке Паскаля имеет вид:
![]()
end; if(x— l) and (a < ![]() and (n < > O) then
writeln ('He flPHHaÅJ1e>KHT') else writeln (
'FIPHHaÅJ1e>KHT')•,
and (n < > O) then
writeln ('He flPHHaÅJ1e>KHT') else writeln (
'FIPHHaÅJ1e>KHT')•,
12. K=2P - l (2P—
1) B ABOH U-IHOM npeÅCTaB,neHHH ![]() HMeeT p extHHHLL p—l HYJ1eü.
MaKCHMaJ1bHOe 3HaqeHHe p onpemejlflemcn Kai' [log2 (N 3aTeM 111)0BepqeTcfl,
HBJ1qeTCH JIH MHCJIO COBepweHHb1M noenyqeHHoro 3Haqe
HMeeT p extHHHLL p—l HYJ1eü.
MaKCHMaJ1bHOe 3HaqeHHe p onpemejlflemcn Kai' [log2 (N 3aTeM 111)0BepqeTcfl,
HBJ1qeTCH JIH MHCJIO COBepweHHb1M noenyqeHHoro 3Haqe![]() p. OHO flBJ1neTCH
COBepmeHHb1M, ecJIH rlpocmoro 3HaqeHHH p MHCJIO 2P — I HBJ1neTCf1
TIPOCTb1M. JIOKaxeM 3TOT
4)aKT.
p. OHO flBJ1neTCH
COBepmeHHb1M, ecJIH rlpocmoro 3HaqeHHH p MHCJIO 2P — I HBJ1neTCf1
TIPOCTb1M. JIOKaxeM 3TOT
4)aKT.
flycTb 2P — I —q. ÅeJIHTeJ1flMH LIHCtna
K, BK,moqafl carvro 4HCJIO K, ![]() CJ1eAY}0L1-we qnctna:
CJ1eAY}0L1-we qnctna: ![]()
![]() q.
q.
3a11HIL1eM CYMMY 3THX meJIHTeJ1eä
![]()
KOTopaq paBHa
![]()
CYMMa B CK06Kax eCTb cyMMa nepBb1x p Y.neHOB reorvreTpuqecK0ä nporpeccHH C nepBb1M LlJ1eHOM I H 3HaMeHaTeJ1eM 2,
OHa paBHa 2P![]()
![]() TaKHM 06pa30M, cyMMa Bcex meJIHTe.nei LIMCJ1a K eCTb
TaKHM 06pa30M, cyMMa Bcex meJIHTe.nei LIMCJ1a K eCTb
![]() 2P.q=2-2P-lq, a CYMMa Bcex
Ae.nure,neä, KPOMe caMoro
2P.q=2-2P-lq, a CYMMa Bcex
Ae.nure,neä, KPOMe caMoro
HHCJ1a ![]() q, paBHa
q, paBHa
AHCJIO P paBH0 cyMMe Bcex CBOHX me.JIHTenei, ga HCKJI}OqeHueM ero caMoro, CJ1eÅOBaTeJ1bHO, OHO flBJIHeTCfl coBepmeHHb1M.
![]()
![]() Если получили несовершенное число,
уменьшаем р на I и снова проверяем, является ли число совершенным.
Если получили несовершенное число,
уменьшаем р на I и снова проверяем, является ли число совершенным.
![]() Совершенные числа получаются для значений
р, равных, например, 2, З, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127.
Совершенные числа получаются для значений
р, равных, например, 2, З, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127.
![]() 13. Запишем уравнение в виде
sXeAk+pY=nYmAt+rX.
13. Запишем уравнение в виде
sXeAk+pY=nYmAt+rX. ![]()
Приравнивая коэффициенты при Х, А и У, получаем:
Xlse=k
Alsk=fll ![]()
![]()
Так как коэффициенты в формуле должны быть взаимно простыми,
то следует найти НОД чисел К и t (алгоритм 3.8). Пусть (К, t)=d. Тогда s (k/d)—
![]() п
(t/d), и числа k/d и t/d являются взаимно простыми, следовательно, n—k/d, а
s=t/d
п
(t/d), и числа k/d и t/d являются взаимно простыми, следовательно, n—k/d, а
s=t/d![]()
![]()
![]()
![]()
![]()
![]() Используя
формулы (*), находим. остальные коэффициенты.
Используя
формулы (*), находим. остальные коэффициенты.
14. По заданным координатам трех вершин мы можем найти площадь треугольника А ВС:
![]()
Если а = 0, то минимальная площадь Sn?itl b/2, если ![]() tnia
а / 2. Если же обе координаты отличны от нуля, то из алгоритма Евклида для
нахождения НОД (а, Ь) следует существование таких целых х и у, что lbx—ayl =
НОД (а, Ь), и именно эти х и у минимизируют площадь треугольника АВС
tnia
а / 2. Если же обе координаты отличны от нуля, то из алгоритма Евклида для
нахождения НОД (а, Ь) следует существование таких целых х и у, что lbx—ayl =
НОД (а, Ь), и именно эти х и у минимизируют площадь треугольника АВС![]()
Нахождение НОД — алгоритм 3.8.
15. Обозначим
![]() (Щ,
Щ). Докажите, что если V делится нацело на S, то в сосуд с помощью банок можно
налить V литров воды, иначе нет.
(Щ,
Щ). Докажите, что если V делится нацело на S, то в сосуд с помощью банок можно
налить V литров воды, иначе нет.
16. Заведем два массива: E [0..N+ l] и S [0..N-F 1]. Элементы массивов — байты. В Е будем хранить текущую частичную сумму
![]()
вычисленную с точностью N+l знаков после запятой (в ячейке Е [i] хранится значение разряда после запятой, т. е. коэффициент при 10 ¯i). В массиве S будет храниться последнее слагаемое частичной суммы, т. е. l/(k— 1)! (опять же в S [i] находится ј-я цифра после запятой, все незначащие цифры, разумеется, нули).
Оценим погрешность формулы ( * ) с учетом равенства
![]()
Погрешность представления числа е будет
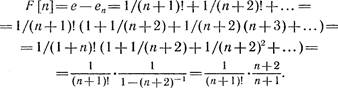
так как F450< lO 1002 то для вычисления, например, [000 знаков после запятой достаточно С— 450 итераций.
Будем делить число, представленное массивом S, на очередное число К. Результат l/k! прибавим к массиву Е. Сложение реализуется так:
perenos : 0; {перенос из предыдущего
разряда} ![]() for i : =N-4-l downto О do begin
for i : =N-4-l downto О do begin
Е = Е [il+S [il+perenos; perenos: = Е [Ц div 10; {формируем новый перенос}
E [i]: mod
10; {корректируем Е ![]() end;
end;
![]() Вычисление новых слагаемых и суммирование
проводится С раз.
Вычисление новых слагаемых и суммирование
проводится С раз.
Рассмотрим процедуру деления S на К. Делить будем так, как это обычно делается вручную — «столбиком»:
{m текущее делимое, т — Longint}
Гог ![]() begin
begin ![]()
Е 69
![]() {дописываем к делимому сзади)
{дописываем к делимому сзади)
{одну цифру}![]()
|
|
div К
|
{находим очередную цифру частного} |
|
|
mod К; |
{и очередное делимое} |
end;
Объясните, почему а [i] лежит в пределах от 0 до 9. Попытаемся
вычислить еп, используя схему Горнера: ![]() + .4+ 1.
+ .4+ 1.
Сначала полагаем Е 1; затем делим «столбиком» число,
представляемое Е, на 450 и запоминаем цифры частного снова в Е. Затем выполняем
Е [О] : ![]() 1, делим Е на 449 и т. д.
1, делим Е на 449 и т. д.
Обратите внимание на то, что во втором способе при
использовании схемы Горнера не надо производить суммирование массивов Е и S,
поэтому скорость работы ![]() увеличивается в 2 раза.
увеличивается в 2 раза.
![]() 17. В переменной стандартного типа такое
большое число не поместится. Будем моделировать возведение 2 в степень п,
вычисляя последовательно 2 1 , 22, У. Цифры полученных на
каждом шаге степеней двойки будем хранить в массиве. В каждой ячейке массива
будем хранить по (например) 4 десятичных цифры числа (т. е. в элементе А [1] —4
последних цифры числа (разряды 0—3), в А [2] —4 предпоследних (разряды 4—7)
17. В переменной стандартного типа такое
большое число не поместится. Будем моделировать возведение 2 в степень п,
вычисляя последовательно 2 1 , 22, У. Цифры полученных на
каждом шаге степеней двойки будем хранить в массиве. В каждой ячейке массива
будем хранить по (например) 4 десятичных цифры числа (т. е. в элементе А [1] —4
последних цифры числа (разряды 0—3), в А [2] —4 предпоследних (разряды 4—7)
![]()
Оценим количество десятичных цифр в числе У, ![]() 1000. Это 10
000 • log2 10+l<15 000 цифр.Количество элементов массива возьмем равным 15
000/4=3750. Введем переменную Nach, в которой будем хранить индекс элемента
массива А, в котором находятся старшие значащие разряды вычисляемого сейчас
числа. При умножении на 2 текущего числа будем умножать на 2 каждый элемент
массива, начиная с первого и заканчивая элементом с номером Nach. Если какой-то
из элементов массива больше 9999, то производим перенос единицы
1000. Это 10
000 • log2 10+l<15 000 цифр.Количество элементов массива возьмем равным 15
000/4=3750. Введем переменную Nach, в которой будем хранить индекс элемента
массива А, в котором находятся старшие значащие разряды вычисляемого сейчас
числа. При умножении на 2 текущего числа будем умножать на 2 каждый элемент
массива, начиная с первого и заканчивая элементом с номером Nach. Если какой-то
из элементов массива больше 9999, то производим перенос единицы ![]() в следующий
разряд. Если был перенос единицы в разряд Nach-}- 1, то значение переменной
Nach увеличим
в следующий
разряд. Если был перенос единицы в разряд Nach-}- 1, то значение переменной
Nach увеличим ![]() на 1.
на 1.![]()
18. Мы можем представить М! в виде произведения простых сомножителей:
![]()
где Ар — показатель степени, с которой
простое число р входит в разложение. Видно, что нулей в конце числа столько же,
сколько нулей в конце произведения 2 ![]() но так как А2>А5, то количество нулей
равно АБ.
но так как А2>А5, то количество нулей
равно АБ.
Для того чтобы найти Аб, необходимо вычислить сумму
![]()
где [ ] — целая часть числа.
Каждое пятое число в произведении N! делится на 5, каждое
двадцать пятое число еще раз делится на 5, ![]() каждое 53 число
еще раз делится на 5 и т. д. Таким образом в ( * ) мы находим, сколько чисел в
произведении М! делится на 5.
каждое 53 число
еще раз делится на 5 и т. д. Таким образом в ( * ) мы находим, сколько чисел в
произведении М! делится на 5.
Фрагмент программы выглядит следующим образом:
repeat
![]() div К; К:
div К; К:![]()
![]() until (k>N);
until (k>N);
![]() Г1осле работы цикла в переменной S будет
находиться 715.
Г1осле работы цикла в переменной S будет
находиться 715. ![]()
19. Найдем простые множители числа Р. Пусть это будут Т, . .
. , РК. Для каждого множителя найдем число ![]() степень, с которой
входит в разложение Р на простые сомножители. Как и в задаче 18, найдем макси
степень, с которой
входит в разложение Р на простые сомножители. Как и в задаче 18, найдем макси![]() 171
171
![]() MaJ1bHb1e qucjla fill, ntk, rraKue,
qT0 N! AeJlUTCfl
Ha pt B CTeneHH rni, HO He AeJIHTCH Ha Pi B CTe[RHH ml + I
MaJ1bHb1e qucjla fill, ntk, rraKue,
qT0 N! AeJlUTCfl
Ha pt B CTeneHH rni, HO He AeJIHTCH Ha Pi B CTe[RHH ml + I ![]() m canemymuee ypaBHeHHe:
m canemymuee ypaBHeHHe:![]()
me div Si H nact HCKOMYK) ctenellb M.
PaCCMOTPHM npv1Mep: N — 15, P == 135.
P![]()
![]() 33 •5, PI
Sl=3, ml — 15 div 3+ 15 div
33 •5, PI
Sl=3, ml — 15 div 3+ 15 div ![]() P2=5, S2= l, 1112 = 15
div 5=3.
P2=5, S2= l, 1112 = 15
div 5=3.
110J1yqaeM, wro M —min {6 div 3, 3 div![]()
06%flCHHTe, noqeMY Mbl ne MOH<eM
ITPHMeHUTb cl)opMY.ny ![]() div P+N div P2+N div PH... .
div P+N div P2+N div PH... .
20. BOCfl0J1b3yeMCfl TeM, ![]() N<4 BblflOJIHneTCfl
HepaBeHCTBO N < (N T. e. pag6HBaTb quceqo Ha cJ1araeMb1e, 60J1bmme 3, He
HMeeT CMb1C,na. BblneJ1f1eM HO qucvqa N CJ1araeMb1e-ABOÜKH, fl0Ka He noun
yquM OCTaTOK MeHb111HÜ JIV160 paBHb1Ü 3 (OCTa rrOK MONCT
6b1Tb JIH60 3,
N<4 BblflOJIHneTCfl
HepaBeHCTBO N < (N T. e. pag6HBaTb quceqo Ha cJ1araeMb1e, 60J1bmme 3, He
HMeeT CMb1C,na. BblneJ1f1eM HO qucvqa N CJ1araeMb1e-ABOÜKH, fl0Ka He noun
yquM OCTaTOK MeHb111HÜ JIV160 paBHb1Ü 3 (OCTa rrOK MONCT
6b1Tb JIH60 3,
JIH60
2). TaK KaK ![]() TO 3aMeHHM Ka>KAb1e -rpu ABOMKA Ha ABe TPOÜKH.
flocnyqeHHoe pa3JIO>KeHHe H flBJ1fl-
TO 3aMeHHM Ka>KAb1e -rpu ABOMKA Ha ABe TPOÜKH.
flocnyqeHHoe pa3JIO>KeHHe H flBJ1fl-
eTC% HCKOMb1M.
Pa36epHTe caMOCTOHTeJ1bHO cjlyqau:
l) He06X'OÅHMO MaKCHMH3HPOBaTb
111)0H3BeneHue H c.oaraeMb1e B pa3JIO>KeHHH LIVIC.na N
AOJl>KHb1 fli)MHaAJ1e![]() lipoMe>KYTKY [A, B], A H B BBOAHTC% flOJlb30BaTe.neM. 2)
Korma He06XOAHMO MHHHMH3HPOBaTb
lipoMe>KYTKY [A, B], A H B BBOAHTC% flOJlb30BaTe.neM. 2)
Korma He06XOAHMO MHHHMH3HPOBaTb![]()
H cJ1araeMb1e B pa3JIO>KeHHH LIHCJ1a N AOJ1>KHb1 mpHHaAenexaTb [A, B], A H B BBOÅflTCfl HOJ1i30BaTeJ1eM.
21.
![]() EcJIH
S TO CY1-ueCTBYfOT eÅMHCTBeHHb1e R} H R2 TaKHe, R = RI •R2=Rl 4-R2.
B0J1ee Toro, HaUMeHbLUee
EcJIH
S TO CY1-ueCTBYfOT eÅMHCTBeHHb1e R} H R2 TaKHe, R = RI •R2=Rl 4-R2.
B0J1ee Toro, HaUMeHbLUee 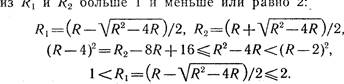 RI H R2 60J1btne I H w•teHbU1e HJIH paBH0 2:
RI H R2 60J1btne I H w•teHbU1e HJIH paBH0 2:
![]()
Итак, если r<4, то разложение на множители закончено, если иначе, то проводим разложение r на два множителя, один из них меньше либо равен 2 (и тем более меньше 4), если другой меньше 4, то процесс не закончен, если иначе, то повторяем факторизацию R до тех пор, пока не получим искомое разложение.
22.
Пусть т/п — текущая несократимая дробь. Покажем, как найти следующую по
значению дробь. Понятно, что она будет среди несократимых дробей вида К / р,
где р может принимать значения от 2 до 15. Учитывая условие К/р> т/п можно
для каждого р прямо вычислять минимальное значение К следующим образом: ![]() При
этом каждая дробь К / р, полученная описанным выше образом, несократима.
При
этом каждая дробь К / р, полученная описанным выше образом, несократима.
 2 to 15 do
2 to 15 do
![]() div п + 1; if
div п + 1; if ![]() then begin i: =k
then begin i: =k ![]()
![]() р; end; end;
р; end; end;
until![]()
![]() 23. Это условие — равенство нулю суммы
всех чисел. Мы всегда можем «перетащить» с помощью последовательности ходов все
ненулевые числа, помечающие вершины, в одну какую-либо вершину. Если сумма всех
чисел равна 0, то после этих ходов окажется, что во всех вершинах записан 0.
23. Это условие — равенство нулю суммы
всех чисел. Мы всегда можем «перетащить» с помощью последовательности ходов все
ненулевые числа, помечающие вершины, в одну какую-либо вершину. Если сумма всех
чисел равна 0, то после этих ходов окажется, что во всех вершинах записан 0.
24. Пусть имеется оптимальное расписание, в котором номера выполняемых работ совпадают с порядковы17,3
ми номерами работ. Тогда этому расписанию
будет соответствовать минимальное значение штрафа. Всякая перестановка в
порядке выполнения двух или более работ уже не может привести к уменьшению
штрафа, ![]() поэтому, переставив местами работы с
номерами К и h+l, мы получим штраф не меньше.
поэтому, переставив местами работы с
номерами К и h+l, мы получим штраф не меньше.
Обозначим через qt время начала выполнения работы i. С учетом представления штрафа это можно записать так:
![]() Е
Е ![]() Е Crq<
Е Crq<![]()
![]() Cx•q+ceqi+ck+eqi+l+ Е
Cx•q+ceqi+ck+eqi+l+ Е![]()
i=k+2
Здесь (к и — время начала выполнения соответственно (К+ 1)-й и К-й работы после перестановки. Заметим, что К-я работа в обоих расписаниях выполнится после того, как будут выполнены предшествующие
К-1 работы, поэтому
![]() tk+l.
tk+l.
В результате получаем:
![]() [К + 1),
[К + 1),
Алгоритм:
1) для всех работ вычислить отношение ti/c;
2) упорядочить работы по возрастанию „этого отношения.
25. В рамках формулировки задачи под корректностью данных программы понимается то, что масса каждого арбуза должна быть положительным числом. Мы знаем и тп. Пусть действительные массы арбузов в ряде nti. Будем обозначать текущие вычисляемые массы Зададим произвольное т; — масса второго арбуза.
![]() nycTb
nycTb ![]() + mí+1)/ 2, Torua, TaK KaK
+ mí+1)/ 2, Torua, TaK KaK
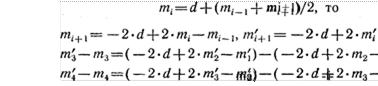
![]()
HaxoÄHM pa3HOCTb ![]() S. Bb1 ĽIHCJ1fleM s.
S. Bb1 ĽIHCJ1fleM s.
S 1. ПОНЯТИЕ ЗАДАЧИ И ПОДЗАДАЧИ
При формулировке любой задачи необходимо определить исходные данные, которые мы будем называть параметрами задачи.
Например, если мы решаем задачу нахождения корней квадратного уравнения ах2 +Ьх+с=0, то эта задача определяется тремя параметрами коэффициентами
![]()
Если же мы хотим решить задачу нахождения среднего арифметического некоторого набора чисел, то параметрами задачи будут количество чисел и их значения.
При этом нас пока не интересует конкретный алгоритм решения задачи. Мы хотим научиться решать задачу, сводя ее к решению подзадач. Здесь удобно думать об алгоритме как о некотором устройстве или некоторой функции, которые преобразуют входные параметры в некоторые выходные данные, являющиеся решением задачи.
Поэтому при описанном выше подходе любая задача может быть формализована в виде некоторой функции, аргументами которой могут являться такие величины, как:
количество параметров; значения параметров.
Здесь и далее в качестве параметров будут рассматриваться целые неотрицательные чис.ла.
Как правило, одним из аргументов задачи является количество параметров задачи. В том случае, когда по
![]()
значению этого параметра можно определить конкретные значения других параметров, мы эти параметры будем опускать. Это обычно делается в случае, когда параметры заданы таблицей. Например, если нам необходимо найти сумму первых К элементов таблицы, то для решения задачи достаточно знать один параметр К, а все остальные параметры можно выбрать из таблицы.
После того как задача формализована (представлена) в виде функции с некоторыми аргументами, определим понятие подзадачи. Здесь и далее в этой главе под подзадачей будем понимать ту же задачу, по с меньшим числом параметров или задачу с тем же числом параметров, но при этом хотя бы один из параметров имеет меньшее значение.
Пример. Найти самую тяжелую из 10 монет.
Для формализации задачи определим функцию «Самая тяжелая монета», аргументами которой являются количество монет (10) и масса каждой из монет. Пока нас не интересует конкретный вид этой функции, для нас важнейшим фактором является то, что она дает правильное решение.
Для данной задачи можно рассмотреть 9 подзадач, которые имеют меньшее число аргументов:
«самая тяжелая монета» из монеты,
«самая тяжелая монета» из 2 первых монет,
«самая тяжелая монета» из З первых монет,
«самая тяжелая монета» из 9 первых монет.
Таким образом, у нашей функции «Самая тяжелая монета» аргументом является количество имеющихся монет, по которому можно определить массу каждой монеты. Следовательно, рассмотренные подзадачи имеют меньшее количество аргументов, чем исходная задача.
Надо отметить, что под подзадачей не следует понимать
некоторые этапы решения задачи, такие, как орга![]() низация ввода и вывода
данных, их упорядочение или решение некоторой части поставленной задачи.
низация ввода и вывода
данных, их упорядочение или решение некоторой части поставленной задачи.![]()
Вопросы для повторения
1. Определить параметры следующих эадач:
а) решить линейное уравнение ах-€ Ь![]()
б) найти наименьшее из N чисел щ, Ф, ... , аду.
![]() Что такое подзадача?
Что такое подзадача?
З. Что может являться аргументами функции, формализующей задачу?
S 2. СВЕДЕНИЕ ЗАДАЧИ К ПОДЗАДАЧАМ
Одним из основных способов решения задач является их сведение к решению такого набора подзадач, чтобы, исходя из решений подзадач, было возможно получить решение исходной задачи.
При этом для решения исходной задачи может потребоваться решение одной или нескольких подзадач.
П р и м е р. Задачу, сформулированную в примере в предыдущем параграфе, можно свести к различным наборам подзадач, например:
найти самую тяжелую из 9 монет, а затем найти самую тяжелую из 2 монет (найденной из 9 и оставшейся) или найти самую тяжелую из 5 монет, затем самую тяжелую из других 5 монет, а затем самую тяжелую из 2 монет, найденных на предыдущих шагах.
Возможны и другие наборы, но нетрудно. заметить, что все они основываются на одной подзадаче: найти самую тяжелую из 2 монет.
В приведенном примере исходная задача сводится к подзадачам с меньшим числом параметров, в данном случае — с меньшим количеством монет.
Используя этот же принцип, можно решить задачу нахождения НОД двух чисел, которая рассматривалась в п. З гл. З.
![]()
Если числа равны, то их НОД равен одному из чисел, т. е.
НОД(м,![]()
стно, что
![]() НОД(м, М).
НОД(м, М).
НОД (N—M, М), а при
Последние соотношения и обеспечивают основной принцип сведения решения задачи к подзадачам: значение одного из параметров стало меньше, хотя их количество и осталось прежним.
![]() Таким образом, решение задачи нахождения
НОД (М, М) при различных значениях N и М сводится к двум подзадачам:
Таким образом, решение задачи нахождения
НОД (М, М) при различных значениях N и М сводится к двум подзадачам:
Вопросы для повторения
Сформулируйте основной принцип сведения задачи к подзадачам.
S З. ПОНЯТИЕ РЕКУРРЕНТНОГО СООТНОШЕНИЯ
Найденный способ сведения решения исходной задачи к решению некоторых подзадач может быть записан в виде соотношений, в которых значение функции, соответствующей исходной задаче, выражается через значения функций, соответствующих подзадачам. При этом важнейшим условием сведения является тот факт, что значения аргументов у любой из функций в правой части соотношения меньше значения аргументов функции в левой части соотношения. Если аргументов несколько, то достаточно уменьшения одного из них.
Следует обратить внимание на то, что соотношения
AOJ1>KHb1 6b1Tb onpeJte,neHb1 Bcex AOnYCTHMb1X 3HaqeHHi apryMeHTOB.
Il p H M e p. HaiTH cyMMY N 3.neMeHTOB
Ta6JIH11b1 A. ![]() flycTb
flycTb ![]() S (N) COOTBeTCTByeT pemeHM10 HCXOÅHOü 3aAa LIH.
3Ta (bYHKLkHfl HMeeT OAHH apryMeHT N — KOJIH L1eCTBO CYMMnpyeMb1X
3JTew•reHTOB Ta6JIH11b1 A. HOHflTHO,
S (N) COOTBeTCTByeT pemeHM10 HCXOÅHOü 3aAa LIH.
3Ta (bYHKLkHfl HMeeT OAHH apryMeHT N — KOJIH L1eCTBO CYMMnpyeMb1X
3JTew•reHTOB Ta6JIH11b1 A. HOHflTHO, ![]() TIOHCKa CYMMb1 N 3J1ewreHTOB
AOCTaTOHHO 3HaTb CYMMY nepBb1X N — 1 3J1eMeHTOB H 3HaqeHue N-ro 3J1ewqeHTa.
F103TOMY pemeHue HCXOAHOÜ
TIOHCKa CYMMb1 N 3J1ewreHTOB
AOCTaTOHHO 3HaTb CYMMY nepBb1X N — 1 3J1eMeHTOB H 3HaqeHue N-ro 3J1ewqeHTa.
F103TOMY pemeHue HCXOAHOÜ ![]() MORI-IO 3anmcaTb B BH-
MORI-IO 3anmcaTb B BH-
Le COOTI--IOLIRHHH
![]()
CJ1enyeT OTMeTHTb, 3T0 COOTH0111eHHe ClipaBeÅJIHBO
![]() JIT060PO KOJIUqeCTBa 3J1eMeHTOB N > l. Ero MO>KHO nepenucaTb B BHJte
JIT060PO KOJIUqeCTBa 3J1eMeHTOB N > l. Ero MO>KHO nepenucaTb B BHJte
![]()
3aMeTHM, LITO Ha npaKTHKe npHMeHflK)Tcfl PiMeK)111Me TOT xe CMb1CJ1 COOTHOi11eHHfl
![]()
![]() 11PHMeHeHHe nepB0P() COOTHomeHHf1
11PHMeHeHHe nepB0P() COOTHomeHHf1 ![]() l, 2, . . . , N H HCflOJ1b3yeTCfl Bbl LIHC,nei-1HH
CYMMb1 N 9,neMe1-1TOB.
l, 2, . . . , N H HCflOJ1b3yeTCfl Bbl LIHC,nei-1HH
CYMMb1 N 9,neMe1-1TOB.
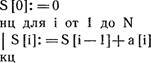
B S [i] XPaHHTCH 3HaqeHHe ![]() S (i).
S (i).
![]() 3necb H Jia,nee B KPVJ1b1X CK06Kax
6YÄYT 3aHHCb1BaTbCfl aprYMeHTb1
3necb H Jia,nee B KPVJ1b1X CK06Kax
6YÄYT 3aHHCb1BaTbCfl aprYMeHTb1 ![]() a B KBaÄpaTHb1X — HHmeKCb1
3J1eMeHTOB MaCCHBa. I-IPH 9TOM HMH
a B KBaÄpaTHb1X — HHmeKCb1
3J1eMeHTOB MaCCHBa. I-IPH 9TOM HMH ![]() H MaccHBa,
H MaccHBa,
B KOTOPOM XPaHHTC51 3HaqeHHe 3T0i ![]() MOPYT C0Bfla
MOPYT C0Bfla![]() naTb.
naTb.
H p H M e q a H e. VIHJ1eKC y S MO>Ket 6biTb onyueu, HO CMblC,a
COOTHomeHHfl 3TOM OCTaeTCH
npe>KHHM. 3T0 CB513aHO C TeM, ![]() BblqHCJ1eHH51 cueAYiouero 3J1erv1eHTa
Ta6JiHUbl S He06XOÅVlMO '3fla"i'b
BblqHCJ1eHH51 cueAYiouero 3J1erv1eHTa
Ta6JiHUbl S He06XOÅVlMO '3fla"i'b ![]() npeÅbmyu.1HV1,
npeÅbmyu.1HV1,
ft p H M e p. BblLIHCJIHTb CYMMY S = I
-l- 1/' x + ![]() +
+ ![]() l/xN X, He paBHOM 0.
l/xN X, He paBHOM 0.
KaK H B npeAb1AYLueM npHMepe, MONKHO 3ar1HcaTb cenenyK)uxee COOTHoweHV1e:
![]()
K0HeHH0, MO>KHO H 9TH COOTHOURHHH
HC110J1b30BaTb![]()
HanncaHHH nporpaMMb1. 9TOM y Hac
B03HUKJ1a HOBaH 3anaqa HaÜTH cnoc06 Bbl t1HCJ1eHHfl a (i), gero
MO>KHO BOCflOJ1b30BaTbC51 Tem xe npqeMOM — 110flblTaTbC51 BblLIUCJlHTb
a (i) qepea 3HaqeH1åe a (i— l). COOTHOL1.1eHHe![]()
3HaqeHHflMH a (i) H a (i l) HMeeT BHA a(i)—a(i— l)/x, i > l, a (0) l.
H03TOMY nocTaBJ1eHhlyro gaAaqy MOM HO
petilVi'1'b coqenyto![]() 06pa30M:
06pa30M:
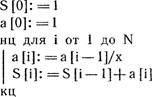 (4.2)
(4.2)
![]() ft p H a H H e. OTMeTHM, '{TO u B 3TOM
cJlyqae HillieKCbl
ft p H a H H e. OTMeTHM, '{TO u B 3TOM
cJlyqae HillieKCbl ![]() S u a MOH<HO OflYCTHTb B CBH3U C TeM, LITO Bbi CiHCJ1eHU}1
Texyu.\ero anetvleuta Kaxaoii H3 Ta6J[HU AOCTaTOLIHO 3HaTb TOJibKO
3naqeHlde npeAb\AYutero 3J1e•MeHTa.
S u a MOH<HO OflYCTHTb B CBH3U C TeM, LITO Bbi CiHCJ1eHU}1
Texyu.\ero anetvleuta Kaxaoii H3 Ta6J[HU AOCTaTOLIHO 3HaTb TOJibKO
3naqeHlde npeAb\AYutero 3J1e•MeHTa.
COOTHomeHHH, CBfl3b1BaiOU..kHe OAHVI H
Te xe ![]() HO c pa3JIHMHb1MH apryMeHTaMH, Ha3b1BakOTCfl pejcgppeHTHbtnu
HO c pa3JIHMHb1MH apryMeHTaMH, Ha3b1BakOTCfl pejcgppeHTHbtnu
![]() pescyppeHTHbt..%u ypagaegua.uu.
pescyppeHTHbt..%u ypagaegua.uu.
![]() Вопросы для повторения
Вопросы для повторения![]()
![]() Являются ли рекуррентными уравнениями
следующие соотношения, где — натуральное число:
Являются ли рекуррентными уравнениями
следующие соотношения, где — натуральное число:![]()
) для
Правильными рекуррентными СООТНОШеНИЯМИ (уравнениями) будем называть такие рекуррентные соотношения, у которых количество или значения аргументов у функций в правой части соотношения меньше количества или, соответственно, значений аргументов функции в левой части соотношения. Если аргументов несколько, то достаточно уменьшения одного из них.
Следует обратить внимание на то, что соотношения должны быть определены для всех допустимых значений аргументов. Поэтому должны быть определены значения функций при начальных значениях параметров.
В приведенных примерах соотношения» связывали функции только с двумя различными параметрами:
![]() — 1), а также a(i) и а
(i— 1) для любого натурального г. При этом были определены начальные значения S
(0) и а (0).
— 1), а также a(i) и а
(i— 1) для любого натурального г. При этом были определены начальные значения S
(0) и а (0).
Отметим, что без этих начальных значений рекуррентное соотношение
![]()
было бы неправильным, так как оно не определено при i= 1.
Конечно, могут быть и более сложные соотношения, связывающие более двух функций.
П р и м ер. Одной из наиболее известных числовых последовательностей являются числа Фибоначчи, которые определяются следующим рекуррентным соотношением:
![]() для натурального 1.
для натурального 1.
![]() В этом случае для вычисления значения F которое хранится в
[М], можно воспользоваться следующим алгоритмом:
В этом случае для вычисления значения F которое хранится в
[М], можно воспользоваться следующим алгоритмом:
![]()
нц для i от 2 до N
![]()
кц
П р и м е ч а ни е. При этом в приведенном фрагменте уже нельзя
просто опустить индексы, хотя в принципе можно вычислить значение F(N) без использования таблицы, но это уже вопрос способа реализации алгоритма.
Пример такой реализации приводится ниже.
![]() нц
для i от 2 до N (4.4)
нц
для i от 2 до N (4.4)
кц
Здесь используется тот факт, что для вычисления текущего элемента таблицы нам достаточно знать только значения двух предыдущих.
![]() Вопросы для повторения
Вопросы для повторения![]()
Являются ли правильными следующие рекуррентные урав-
![]() ай 2, i — натуральное; (i— для
i>2,
ай 2, i — натуральное; (i— для
i>2,
для i>'2, для i> l, для i>2,
S 5. СПОСОБ ОРГАНИЗАЦИИ ТАБЛИЦ
Как уже говорилось раньше, подзадача может быть формализована
в виде функции, которая *зависит от одного или нескольких аргументов. Если мы
возьмем ![]() таблицу, у которой количество элементов
равно количеству всех возможных различных наборов аргументов функции, то
каждому набору аргументов может быть поставлен в соответствие элемент таблицы.
Вычислив элементы таблицы (решения подзадач), можно найти и решение исходной задачи.
таблицу, у которой количество элементов
равно количеству всех возможных различных наборов аргументов функции, то
каждому набору аргументов может быть поставлен в соответствие элемент таблицы.
Вычислив элементы таблицы (решения подзадач), можно найти и решение исходной задачи.
5.1. Организация одномерных таблиц
![]() Одним из способов организации таблиц
является такой, когда размерность таблицы определяется количеством аргументов у
функции, соответствующей подзадаче.
Одним из способов организации таблиц
является такой, когда размерность таблицы определяется количеством аргументов у
функции, соответствующей подзадаче.
Пример. Рассмотрим задачу нахождения произведения 10 элементов таблицы А.
Пусть функция P (l0) соответствует решению нашей исходной задачи. В данном случае у функции только один параметр — количество элементов. Для поиска произведения 10 элементов достаточно знать произведение первых 9 элементов и значение 10-го элемента. Поэтому решение исходной задачи можно записать в виде соотношения Следовательно, это соотношение может быть определено для любого i, 10:
На практике для рассматриваемой задачи чаще используется рекуррентное соотношение, имеющее тот же смысл, но с другим начальным значением:
![]() l).aj при i> l,
l).aj при i> l,![]()
Приведем алгоритм, реализующий данное рекуррентное соотношение:
![]()
нц для i от 1 до N
![]()
кц
Так как у нашей функции один аргумент — количество
сомножителей, то для решения задачи достаточно использовать одномерную таблицу.
При этом количество элементов таблицы определяется количеством различных
значений аргумента. В приведенном примере размерность массива равна 10. Если бы
мы решали задачу ![]() поиска произведения 20 элементов, то для
реализации рекуррентного соотношения нам было бы достаточно одномерной таблицы
с 20 элементами.
поиска произведения 20 элементов, то для
реализации рекуррентного соотношения нам было бы достаточно одномерной таблицы
с 20 элементами.
TaKHM 06pa30M, pa3MepHOCTb Ta6JIHUbl,
AOCTaTO t1Hafl ![]() peanH3a11HH peKyppeHTHbix COOTHOIJRHHÜ, onpeAeJ1fl
peanH3a11HH peKyppeHTHbix COOTHOIJRHHÜ, onpeAeJ1fl![]() eTCH KOJImqeCTBOM apryMeHTOB y
d)YHKÅHÜ, COOTBeTCTBYIOl-unx 110Å3aaaqaM. KOJIHqeCTBO xe
9.neMeHTOB no Kaxmoi
eTCH KOJImqeCTBOM apryMeHTOB y
d)YHKÅHÜ, COOTBeTCTBYIOl-unx 110Å3aaaqaM. KOJIHqeCTBO xe
9.neMeHTOB no Kaxmoi ![]() pa3MepHocTH (KOJIHqeCTBO 3J1eMeHTOB B CTPOKax, CTOJ16qax)
onpeÅeJ1qeTcfl KOJIqqeCTBOM B03MO>KHb1X 3HaqeHHü COOTBeT
pa3MepHocTH (KOJIHqeCTBO 3J1eMeHTOB B CTPOKax, CTOJ16qax)
onpeÅeJ1qeTcfl KOJIqqeCTBOM B03MO>KHb1X 3HaqeHHü COOTBeT![]() CTBYK)1.uero apryMeHTa.
CTBYK)1.uero apryMeHTa.
5.2. OpraHH3aunq ABYMePHb1X Ta6J1%14
Ellie pa3 06paTHM BHUMaHUe Ha TO, Hac HOKa He
![]()
oqeHb HHTepecyeT peaJIH3auuH a.]1FOPHTMa, KOTOPOÜ
MHHHMH3mpyeTcn rraKaq xapaKTepncTHKa, KaK
pa3Mep MC110J1b3yeM0i onepaTHBH0ü naMflTH. ByaeM C tlHTaTb, qT0
naM51TV1 K0Mflb10Tepa AOCTaTO LIHO xpaHeHHH COOTBeT![]() CTBYE011keÜ Ta6JIHUb1.
CTBYE011keÜ Ta6JIHUb1.
![]()
9J1eMeHTOB Ta6JIHUb1 B, KOTOPb1e pacfl0J10xeHb1 JleBee H Bblme 1103HUHH (i, j), BKJ1kO%H rraK>Ke 1103muuk0 (i, j). I-IPH
9TOM CLIHTaeTCH, q rro ![]() (l, l) — BePXHflH sneBaH fl03H
(l, l) — BePXHflH sneBaH fl03H![]() 11PflMoyrOJ1bHOÜ Ta6JIHUb1,
HHTepecyfouxaq Hac qacTb
11PflMoyrOJ1bHOÜ Ta6JIHUb1,
HHTepecyfouxaq Hac qacTb
Ta6JIHUb1 BblAeJ1eHa npu ![]()
|
all am |
an a32 |
a13 au a33 au |
a 15 a16 a25 a26 a 35 a36
|
|
|
a43 au |
"145 |
a46 |
|
a51 |
a52 |
a53 a54 |
a55 |
a56 |
flycTb T (i, j) 0603HaqaeT ![]() Bb1 14HCJ1flK)L11YK) 9J1eMeHT B [i,
Bb1 14HCJ1flK)L11YK) 9J1eMeHT B [i,![]()
OnpemeJIHM cHaqa,na 3HaqeHHH 3.neMeHTOB Ta6JIMUb1 B, paC110J10xeHHb1X B nepB0i CTPOKe H B nepB0M CTOJ16Lte. TIOJ1yquM'.
![]()
I), А [1, ј]} при ј![]()
![]() 1, 1), А [ђ, 1]} при
i>2.
1, 1), А [ђ, 1]} при
i>2.
Эти соотношения следуют из того, что в этих случаях интересующая нас область матрицы А ограничена только элементами первой строки или первого столбца матрицы.
При ![]() для этой функции можно записать следующее
рекуррентное соотношение:
для этой функции можно записать следующее
рекуррентное соотношение:
T(i,
![]() Действительно, величина максимальной величине элементов
таблицы А в той ее части, которая определяется значением индексов i— l и ј, а
величина T(i, ј— 1)— максимальной величине элементов таблицы А, определяемой
индексами i и ј— 1. Поэтому эти величины учитывают значения всех элементов
матрицы А в той ее части, которая определяется значениями индексов i и ј за
исключением одного элемента А [i, ј].
Действительно, величина максимальной величине элементов
таблицы А в той ее части, которая определяется значением индексов i— l и ј, а
величина T(i, ј— 1)— максимальной величине элементов таблицы А, определяемой
индексами i и ј— 1. Поэтому эти величины учитывают значения всех элементов
матрицы А в той ее части, которая определяется значениями индексов i и ј за
исключением одного элемента А [i, ј].
Для реализации этих рекуррентных соотношений достаточно двумерной (прямоугольной) таблицы, так как у функции Т два аргумента. Важно отметить, что при этом мы можем отождествить величины Т (Ј, ј) и В [Ј, ј], Тогда фрагмент алгоритма можно записать следующим образом:
![]()
нц для ј от 2 до 6
![]()
нц для i от 2 до 5
![]() = тах (В [ћ — 1,
= тах (В [ћ — 1,![]()
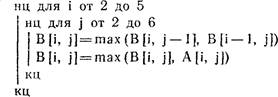
![]() Вопросы для повторения
Вопросы для повторения![]()
![]() 1,
Определить размеры одномерных таблиц дл; следующих рекуррентных уравнений, где
i'— натуралъное:
1,
Определить размеры одномерных таблиц дл; следующих рекуррентных уравнений, где
i'— натуралъное:![]()
1000,
2. Определить размеры двумерных таблиц для следующих рекуррентных уравнений:
![]() 1), aij)
для 2<i<5,
1), aij)
для 2<i<5,
для![]()
1) для ![]() 10.
10.
для 1![]()
S 6. СПОСОБ вычисј1Ения ЭЛЕМЕНТОВ ТАБЛИЦЫ
После того как найдено сведение задачи к подзада-
чам и определены рекуррентные соотношения, соответствующие этому сведению, необходимо определить наиболее рациональный способ вычисления элементов таблицы.
6.1. Вычисление элементов одномерной таблицы
Для одномерной таблицы таким способом обычно является последовательное вычисление элементов, начиная с первого.
Пример. Определить, сколькими различными способами можно подняться на 10-ю ступеньку лестницы, если за один шаг можно подниматься на следующую ступеньку или через одну.
Пусть К (10)— задача поиска количества способов подъема на 10-ю ступеньку. Определим i„10 подзадачу нашей задачи как задачу поиска количества способов подъема на Ј-ю ступеньку.
Исходя из условия задачи, на 10-ю ступеньку можно подняться непосредственно с 8-й и 9-й. Поэтому, если мы знаем количество способов подъема К (8) и К (9) на 8-ю и 9-ю ступеньки, то количество способов подъема на 10-ю может быть определено как k(10)—
![]()
Такое соотношение получается потому, что любой способ подъема на 8-ю ступеньку превращается в способ подъема на 10-ю добавлением перешагивания через 9-ю, а любой способ подъема на 9-ю ступеньку превращается в способ подъема на 10-ю добавлением подъема с 9-й на 10-ю. Все эти способы различны.
Аналогичное соотношение справедливо для любой ступеньки i, начиная с третьей:
![]()
Осталось определить значения k(l) и К (2), которые равны: К К (2)—2.
Следовательно, для решения задачи достаточно одномерной таблицы с 10 элементами, для которой необходимо последовательно вычислить значения элементов таблицы согласно приведенным выше рекуррентным соотношениям.
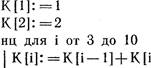 —2] кц
—2] кц
![]() П р и м е ча н и е. Полученные
рекуррентные соотношения не отличаются от рекуррентных соотношений примера 6,
поэтому могут быть реализованы без использования таблицы.
П р и м е ча н и е. Полученные
рекуррентные соотношения не отличаются от рекуррентных соотношений примера 6,
поэтому могут быть реализованы без использования таблицы. ![]()
6.2. Вычисление элементов двумерной таблицы
Пример. В таблице с N строками и М столбцами, состоящей из 0 и 1, необходимо найти квадратный блок максимального размера, состоящий из одних единиц. Под блоком понимается множество элементов соседних (подряд идущих) строк и столбцов таблицы. Интересующая нас часть таблицы выделена.
Положение любого квадратного блока может быть определено его размером и положением одного из его углов.
![]() Пусть T(i, ј) — функция, значение которой
соответствует размеру максимального квадратного блока, состоящего из одних
единиц, правый нижний утол которого расположен в позиции (i, ј). Функция T(i,
ј) вычисляет элемент таблицы В [i, ј]. Для приведенной выше таблицы значения Т
(Ј, ј) будут иметь вид:
Пусть T(i, ј) — функция, значение которой
соответствует размеру максимального квадратного блока, состоящего из одних
единиц, правый нижний утол которого расположен в позиции (i, ј). Функция T(i,
ј) вычисляет элемент таблицы В [i, ј]. Для приведенной выше таблицы значения Т
(Ј, ј) будут иметь вид:
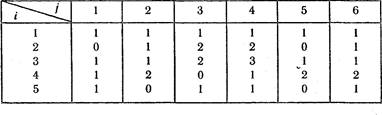
Таким образом, наша задача свелась к вычислению максимального значения функции Т при всевозможных значениях параметров i и ј. Этой функции может быть поставлена в соответствие таблица размера N•M.
![]() расположенных в первой строке и в первом
столбце.
расположенных в первой строке и в первом
столбце.
![]() Получим: В О, Ц, ва,
[I, ј] при ј>2, в (Ј, [Г, 1] при i>2.
Получим: В О, Ц, ва,
[I, ј] при ј>2, в (Ј, [Г, 1] при i>2.
Данные соотношения следуют из того, что в этих случаях рассматриваемая область матрицы А содержит только один элемент матрицы.
При ![]() для этой функции можно записать следующие
рекуррентные соотношения:
для этой функции можно записать следующие
рекуррентные соотношения:
В [i, если А [Ј, jl=0
![]() 1], В [i— l, ј— 1]} + l,
1], В [i— l, ј— 1]} + l,
Первое соотношение показывает, что размер максимального
единичного блока с правым нижним углом в позиции (i, ј) равен нулю в случае А
[i,![]()
Величина B[i, ј 1] соответствует максимальному размеру единичного блока таблицы А с правым нижним углом в позиции (i, ј— 1). Тоеда размер единичного блока с правым нижним углом в позиции (Ј, ј) не превышает величину В [i, ј— 1 Н- 1, так как к блоку в позиции (Ј— 1, ј) мог добавиться только один столбец.
Величина В [Ј— 1, ј— 1] соответствует максимальному размеру
единичного блока таблицы А с правым нижним углом в позиции (Е— — 1). Тогда
размер единичного блока с правым нижним углом в позиции (Ј, ј) не превышает
величину В [i— 1, ј— 1]-F 1, так как к блоку в позиции (i— —1) могли добавиться
только одна строка и один столбец. ![]()
Итак, размер единичного блока с правым нижним углом в позиции
(i, ј) равен min {В [ђ— ![]() 1],
1],
B [i— l,![]()
![]()
нц для ј от 2 до 6 l B [l, Ј]: = ![]() нц для i от 2 до 5
нц для i от 2 до 5
![]()
![]() min
(В [i, j — ll, вр 1,
min
(В [i, j — ll, вр 1, ![]() min (В [i, ј]. вр 1.
min (В [i, ј]. вр 1.![]()
6.3. Вычисление элементов двумерной таблицы с дополнительными ограничениями
Пример. На складе имеется 5 неделимых предметов. Для каждого предмета известна его стоимость (в рублях) и масса (в килограммах). Величины стоимости и массы являются натуральными числами. Наша цель состоит в том, чтобы определить максимальную суммарную стоимость предметов, которые можно унести со склада при условни, что суммарная масса предметов не должна превышать 16 кг.
Пусть элемент Ci таблицы С соответствует стоимости ![]() предмета,
а элемент МЈ таблицы М — массе Ј-го предмета. Будем считать, что предметы
пронумерованы в порядке их следования в таблицах.
предмета,
а элемент МЈ таблицы М — массе Ј-го предмета. Будем считать, что предметы
пронумерованы в порядке их следования в таблицах.
[92
Пусть Т обозначает функцию, значение
которой соответствует решению нашей зада ди. Аргументами у этой функции
является количество предметов (по этому -аргументу можно определить их
стоимости и массь1 соответствующих предметов), а также максимальная ![]() суммарная
масса, которую можно унести.
суммарная
масса, которую можно унести.
Для нашей задачи Т (5, 16) определим подзадачи T(i, ј), где i
обозначает количество начальных предметов, из которых можно осуществлять выбор,
а ј определяет максимально возможную суммарную массу уноси![]() мых
предметов. Отметим, что
мых
предметов. Отметим, что ![]() таким образом
таким образом ![]() первый параметр i
определяет как количество предметов для подзадачи, так и значения их стоимостей
и масс из таблиц С и М.
первый параметр i
определяет как количество предметов для подзадачи, так и значения их стоимостей
и масс из таблиц С и М. ![]()
Определим сначала начальные значения функции Т. При нулевых значениях одного из аргументов значение функции равно нулю:
![]()
![]() при j>l,
при i> l.
при j>l,
при i> l.
Определим возможные значения функции Т (
г, ј) при ![]() ненулевых значениях аргументов.
ненулевых значениях аргументов.
Решение подзадачи, соответствующей функции Т (Ј, ј), может быть сведено к двум возможностям: уносится ли при наилучшем решении предмет с номером или нет.
![]() Если предмет не уносится, то решение
задачи с i предметами сводится к решению подзадачи с
Если предмет не уносится, то решение
задачи с i предметами сводится к решению подзадачи с
• предметами, т. е.
ТС,![]()
Если предмет с номером i уносится, то это
умень![]() шает максимально возможную суммарную
массу для
шает максимально возможную суммарную
массу для ![]() первых предметов на величину М [i],
одновременно при этом увеличивая значение решения для оставшихся предметов T(i—
1, j—M[i]) на величину С т. е.
первых предметов на величину М [i],
одновременно при этом увеличивая значение решения для оставшихся предметов T(i—
1, j—M[i]) на величину С т. е. ![]()
т
(Ј, т (Ј— 1, ем![]()
7 Информатика, 8—9 кл. i93
При этом необходимо учитывать, что вторая ситуация возможна только тогда, когда масса Ј-го предмета не больше значения ј.
Теперь для получения наилучшего решения нам необходимо
выбрать лучшую из этих двух возможностей. Поэтому рекуррентное соотношение при
и ј ![]() имеет вид:
имеет вид:
ТО,![]()
![]()
Пусть заданы следующие значения стоимости и массы для 5 предметов:
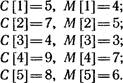
Таблица значений функции Т, которую мы также назовем 7', выглядит следующим образом:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 о О о |
о 0 О о |
о о О 0 о о |
о 0 4 4 4 |
о 5 5 5 5 5 |
5 7 7 7 7 |
5 7 7 7 8 |
о 5 7 9 9 9 |
5 7 11 |
о 5 12 12 12 12 |
0 5 12 12 13 |
0 5 12 12 14 15 |
5 12 16 16 16 |
5 16 16 17 |
0 5 5 12 12 16 16 18 20 19 20 |
5 12 16 21 21 |
|
|
|
|||||||||||||||||
|
2 |
|||||||||||||||||
|
з |
|||||||||||||||||
|
4 |
|||||||||||||||||
|
5 |
|||||||||||||||||
Следовательно, решение задачи 16)= 21, т. е ![]() можно унести
предметов на 21 рубль.
можно унести
предметов на 21 рубль.
Приведем одну из возможных реализаций.
 0T I mo 16
0T I mo 16
KLI
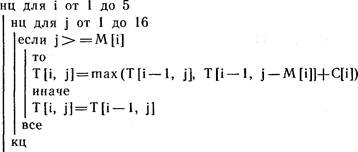
KII
3AÅA4U nOBTOPEHHA
i. K KaKHM 110A3maqaM MO>KeT CBOÅHTbCH [IOHCK OAHOÜ 4)aJ1bL11HBOä MOHeTb1 cpeÅH 27 MOHeT, eCJIH H3BeCTHO, HTO OHa Jlerqe mpyrmx, a BCe OCTaJ1bHb1e HMeK)T OAHHaKOBY10 Maccy?
2. K KaKHM 110Ä3amauaM MO*CT CBOAMTbCH aanaqa Bbl-
t.1MCJTeHHH 3HaqeHHfl N! (N! = I •2•3•... •N)?
3. K KaKHM 110A3amaqaM MONCT CBOÄHTbCfl 3anaqa TIOHCKa CYMMb1 110JIO>KHTeJ1bHb1X 3J1eMeHTOB Ta6JIH11b1, COCTO%uxeü H3 10 3J1eMeHTOB?
4.
HBJTH}OTCH JIH
npaBHJ1bHb1MH peKyppeHTHb1e ypaBHeHUH,  me • — HaTypaJ1bHoe MHCJIO:
me • — HaTypaJ1bHoe MHCJIO:
r) S(i)—S(i div 2)+ 1 i > 2,
![]()
195
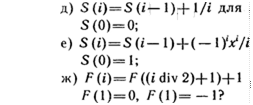 для i>l,
для i>l,
5. Указать, при каких размерах таблиц могут быть реализованы рекуррентные соотношения:
![]() а)
а)
— 1), ау) ДЛЯ
Vi_I. Получить (.'2, (Уз, . . . , оп,
где п — заданное натуральное число.
7. Пусть
хо— с, xl=d•, ![]() Получить
Получить ![]() х где п, Ь, с, d—
заданные натуральные числа. 8. Пусть
х где п, Ь, с, d—
заданные натуральные числа. 8. Пусть ![]() •
• ![]() лучить из, щ, . . . ,
ин, где п — заданное натуральное число.
лучить из, щ, . . . ,
ин, где п — заданное натуральное число.
9.
Пусть ![]() ai -К- ai_2. Получить ф, аз,
ai -К- ai_2. Получить ф, аз,
![]() ал, где п — заданное натуральное
число.
ал, где п — заданное натуральное
число.
10. Пусть
![]()
![]() +bi_l.
Получить ф, аз, п — натуральное число.
+bi_l.
Получить ф, аз, п — натуральное число.
11. Пусть щ = и, 2 bi_l 0i_l, 2 + Ь. 1. Получить Ф, аз, . . . , Ь где п — натуральное число, а и, о — некоторые действительные числа.
12.
![]() Пусть а—
Пусть а— ![]() 1, bl
1, bl
п — натуральное число.
13. Пусть а— 1, Ь)
+3ibi_t. Получить Ъ, аз, ..в, п, 2, Ьз, . . . , Ьп, где п — натуральное число.
14. Bb1HHCJIHTb 31--łaqeHHe Ap06ei.
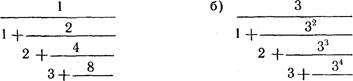
![]()
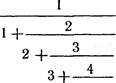 r)
r) 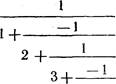
![]()
![]() A)
A) 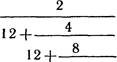
16
12+![]()
![]() 12+
12+![]()
12

![]()
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ
1. Составить алгоритм определения количества шесгизначных «счастливых» трамвайных билетов, у которых сумма первых трех цифр совпадает с суммой трех последних.
2. Составить
алгоритм определения количества ![]() «счастливых» билетов, у КОТОРЫХ сумма
первых N цифр равна сумме последних N цифр; М
«счастливых» билетов, у КОТОРЫХ сумма
первых N цифр равна сумме последних N цифр; М ![]() произвольное
натуральное число.
произвольное
натуральное число.
З. Найти количество п-значных чисел в десятичной системе
счисления, у каждого из которых сумма цифр равна К. При этом в качестве
п-значного числа мы допускаем и числа, начинающиеся с одного или нескольких
нулей. Например, 000102 рассматривается как шес![]() тизначное число, сумма
цифр которого равна З.
тизначное число, сумма
цифр которого равна З.
4. Фишка
может двигаться по полю длиной N только ![]() вперед. Длина хода
фишки не более К. Найти число различных путей, по которым фишка может пройти
поле от позиции до позиции М. П р и м е р. N=4, К—2.
вперед. Длина хода
фишки не более К. Найти число различных путей, по которым фишка может пройти
поле от позиции до позиции М. П р и м е р. N=4, К—2.
Возможные длины ходов:![]()
О т в е т: З.
5. Покупатель
имеет купюры достоинством А], ..., А ![]() а продавец — В В . Найти максимальную
стоимость товара Р, который покупатель не может купить, потому что нет
возможности точно рассчитаться за этот товар с продавцом, хотя денег на покупку
его достаточно.
а продавец — В В . Найти максимальную
стоимость товара Р, который покупатель не может купить, потому что нет
возможности точно рассчитаться за этот товар с продавцом, хотя денег на покупку
его достаточно.
6. У покупателя есть п монет достоинством Hl, ... , щ. У продавца есть т монет достоинством Щ, . .., Вт. Может ли покупатель приобрести вещь стоимостью S так, чтобы у продавца нашлась точная сдача (если она необходима)?
7. По матрице А [1..N, l..N] построить матрицу В [l..N, I..N]. Элемент B[i, /] равен максимальному из элементов матрицы А, принадлежащему части, ограни-
ченной справа диагоналями, проходящими через А [i, ј] (см. таблицу).

8. Задана матрица натуральных чисел А [1..п, l..m]. За каждый проход через клетку (i, ј) взимается штраф А [i, П. Необходимо минимизировать штраф и:
![]() а) пройти из
какой-либо клетки 1-й строки 8 п-ю строку, при этом из текущей клетки можно
перейти в любую из З соседних, стоящих в строке с номером, на 1 большим; б)
реализовать пункт а) для перехода из клетки (1, 1) в клетку (п, т).
а) пройти из
какой-либо клетки 1-й строки 8 п-ю строку, при этом из текущей клетки можно
перейти в любую из З соседних, стоящих в строке с номером, на 1 большим; б)
реализовать пункт а) для перехода из клетки (1, 1) в клетку (п, т).
9. Выпуклый
![]() N>3, задается координатами своих
вершин в порядке обхода по контуру. Разбить его на треугольники (N—3)
диагоналями, не пересекающимися, кроме как по концам, таким образом, чтобы: а)
сумма их длин была минимальной;
N>3, задается координатами своих
вершин в порядке обхода по контуру. Разбить его на треугольники (N—3)
диагоналями, не пересекающимися, кроме как по концам, таким образом, чтобы: а)
сумма их длин была минимальной;
б) самая длинная из диагоналей имела наименьшую длину.
10. Пусть ф, ..., ат) и
b2, . ![]() заданные строки символов.
заданные строки символов.
Обозначим через d (х, у) минимальное количество вставок, удалений и замен символов, которое необходимо для преобразования х в у.
Например: d(ptslddf, tsg[dds)=3 удаление р вставка д замена
ptslddf![]() tslddi
tslddi![]() tsglddf tsgldds
tsglddf tsgldds
Для заданных строк х и у определить d (х, у),
11. Даны две строки х и у. Строка х состоит из нулей и единиц, строка у состоит из символов А и В. Можно ли строку х преобразовать в строку у по следующему правилу: цифра 0 преобразуется в непустую последовательность букв А, а цифра — либо в непустую последовательность букв А, либо в непустую последовательность букв В?
12. Пусть известно, что
для перемножения матрицы размера п Х т на матрицу размера т ХК требуется ![]() операций,
и в результате получается матрица размера п ХК.
операций,
и в результате получается матрица размера п ХК.
Необходимо определить, какое минимальное число операций
потребуется для перемножения s матриц Аз, ![]() ,4s, заданных своими
размерами (i). При этом можно перемножать любые две рядом стоящие матрицы.
,4s, заданных своими
размерами (i). При этом можно перемножать любые две рядом стоящие матрицы.
Замечание:![]()
![]() число строк в матрице
Д, т (i)— число сто.лбцов в матрице Д,
число строк в матрице
Д, т (i)— число сто.лбцов в матрице Д,
![]()
13. а) Из заданной числовой последовательности А [1.,N] вычеркнуть минимальное количество элементов так, чтобы оставшиеся образовали строго возрастающую последовательность (или, что то же, найти максимальную длине строго возрастающую подпоследовательность последовательности А).
б) Из заданной числовой последовательности А [l..N] вычеркнуть минимальное число элементов таким образом, чтобы в оставшейся подпоследовательности каждый последующий элемент был больше предыдущего, кроме, быть может, одной пары соседних элементов (одного «разрыва» возрастающей подпоследовательности).
Например: 2, З, 2, 4, З, 4, 6);
Искомая подпоследовательность (1, 2, З, 2, З, 4, 6). Разрыв подчеркнут.
в) Из заданной числовой последовательности А [l..N]
вычеркнуть минимальное число элементов так, чтобы в оставшейся
подпоследовательности каждый последующий элемент был больше предыдущего, кроме,
быть может, т пар соседних элементов (сформировать возрастающую
подпоследовательность с т «разрывами»).![]()
14.
Из элементов заданной последовательности целых чисел построить такую
максимально длинную подпоследовательность чисел, чтобы каждый последующий
элемент подпоследовательности делился нацело на пре![]() дыдущий.
дыдущий.
15.
Задаются число п — размерность пространства и размеры М п-мерных
парал.лелепипедов (аи, . aiii)' ![]() т. Параллелепипед может располагаться
т. Параллелепипед может располагаться ![]() в
пространстве любым из способов, при которых его ребра параллельны осям
координат.
в
пространстве любым из способов, при которых его ребра параллельны осям
координат.![]()
Найти максимальную последовательность вкладываемых друг в друга параллелепипедов.
16.
Заданы три числа а, Ь, с. Можно ли представить число а таким ![]() образом,
чтобы
образом,
чтобы
где b<x х а, Ь, с — целые? Лучшим считается алгоритм, находящий такое представление с наименьшим числом множителей. Предусмотреть вариант, когда такого представления не существует.
170 Схема железнодорожной сортировочной станции приведена на рисунке 29.
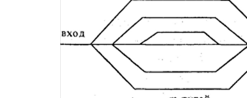
т путей
Рис. 29
Пути пронумерованы от 1 до т.
На вход в произвольном порядке подается п вагонов,
занумерованных числами от до п. Каждый вагон ![]() необходимо направить
на один из станционных путей, откуда его затем переводят на выход. На любой
путь можно направить произвольное количество вагонов. На выходе необходимо
сформировать состав с номерами вагонов в возрастающем порядке.
необходимо направить
на один из станционных путей, откуда его затем переводят на выход. На любой
путь можно направить произвольное количество вагонов. На выходе необходимо
сформировать состав с номерами вагонов в возрастающем порядке.
Описать алгоритм, который по данным п, т и исходной последовательности номеров вагонов отвечает на вопрос, можно ли выполнить требуемую сортировку.
18. Возвести число А в натуральную степень п за как можно меньшее количество умножений.
19. Заданы две последовательности чисел z и у. Можно ли получить последовательность вычеркиванием элементов из у?
20. Вводятся две последовательности х и у. Найти максимальную по длине последовательность г, которую можно получить вычеркиванием элементов как из х, так и из у.
Например, для x=«abacs», y=«dalas» последовательность «aas».
21. Пусть х и у— две бинарных последовательности (т. е. элементы последовательностей нули и единицы); х и у можно рассматривать как запись в двоичной форме некоторых двух натуральных чисел.
Найти максимальное число 2, двоичную запись которого можно получить вычеркиванием цифр как из х, так и из у. Ответ выдать в виде бинарной последовательности.
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
1. Существует игра для одного игрока,
которая начи![]() нается с задания цепочки с N вершинами.
Пример графического представления цепочки показан на рисунке 30, а, где N=4.
Для каждой вершины цепочки задается значение — целое число, а для каждого ребра
—
нается с задания цепочки с N вершинами.
Пример графического представления цепочки показан на рисунке 30, а, где N=4.
Для каждой вершины цепочки задается значение — целое число, а для каждого ребра
—
1
а 
З
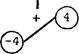
Рис. 30
метка операции +(сложение) либо * (умножение). Ребра цепочки пронумерованы от I до N— l. Каждый ход состоит из следующих шагов:
выбирается ребро Е и две вершины Vl и V2, которые соединены ребром Е; ребро Е и вершины Щ и V2 заменяются новой вершиной со значением, равным результату выполнения операции, определенной меткой ребра Е, над значениями вершин Щ и V2.
Игра заканчивается, когда больше нет ни одного ребра. Результат игры — это число, равное значению оставшейся вершины.
Пример и гр ы. Игрок начал игру с удаления ребра 2 (рис. 30, б), затем — ребра З (рис. 30 , в), наконец, ребра 1. Результатом игры будет число 0 (рис. 30, г).
Каписать программу, которая по заданной цепочке вычисляет максимальное значение оставшейся вершины и выводит список всех тех ребер, удаление которых на первом ходе игры позволяет получить это значение.
Входные данные находятся в файле с именем CHAIN.lN и имеют следующую структуру.
В первой строке находится число N 100) — количество вершин цепочки.
В каждой из последующих N строках находятся ![]() значения в
вершинах целые числа.
значения в
вершинах целые числа.
В каждой из последующих N—l строк находится тип операций (-4- или * ) для соответствующего ребра. Ребро с номером i соединяет вершины с номерами i и
В выходной файл с именем CHAIN.OUT требуется вывести
максимально возможный результат.![]()
2. В связи с эпидемией гриппа в больницу направля![]() ется
А больных гриппом «А» и В больных гриппом «В». Больных гриппом «А» нельзя
помещать в. одну палату с больными гриппом «В». Имеется информация об общем
количестве палат Р в больнице, пронумерованных от I до Р, и о распределении уже
имеющихся там больных.
ется
А больных гриппом «А» и В больных гриппом «В». Больных гриппом «А» нельзя
помещать в. одну палату с больными гриппом «В». Имеется информация об общем
количестве палат Р в больнице, пронумерованных от I до Р, и о распределении уже
имеющихся там больных.
Написать программу, определяющую максимальное количество больных М, которое больница в состоянии принять. При размещении новых больных не разрешается переселять уже имеющихся больных из палаты в палату.
Входные данные находятся в текстовом файле и имеют следующую структуру:
в первой строке находится число А (целое,![]()
< 1 00); во второй строке — число В
(целое, ![]() 100); в третьей строке — число Р
(натуральное, Р <20); в каждой из последующих Р строк находятся З числа п,
а, Ь, разделенных пробелом, где п — вместимость палаты, а — количество уже
имеющихся в палате больных гриппом «А», Ь — количество уже имеющйхся в палате
больных гриппом «В». Информация о вместимости палат вводится последовательно
для палат с номерами
100); в третьей строке — число Р
(натуральное, Р <20); в каждой из последующих Р строк находятся З числа п,
а, Ь, разделенных пробелом, где п — вместимость палаты, а — количество уже
имеющихся в палате больных гриппом «А», Ь — количество уже имеющйхся в палате
больных гриппом «В». Информация о вместимости палат вводится последовательно
для палат с номерами
![]() Р. Числа п, а, Ь — целые неотрицательные
меньше l00.
Р. Числа п, а, Ь — целые неотрицательные
меньше l00.
Выходные данные должны быть записаны в текстовый файл и иметь следующий формат:
в первой строке должно находиться число М;
если все поступившие больные размещены, то во ![]() второй строке должны
находиться номера палат, разделенные пробелом, куда помещаются больные гриппом
«А».
второй строке должны
находиться номера палат, разделенные пробелом, куда помещаются больные гриппом
«А».
![]() З. Задается натуральное число N 999).
Двое играющих называют по очереди числа, меньше 1000, по следующим правилам.
Начиная с числа N, каждое новое число должно увеличивать одну из цифр
предыдущего числа (возможно, незначащий нуль) на 1, 2 или З, Проигравшим
считается тот, кто называет число 999.
З. Задается натуральное число N 999).
Двое играющих называют по очереди числа, меньше 1000, по следующим правилам.
Начиная с числа N, каждое новое число должно увеличивать одну из цифр
предыдущего числа (возможно, незначащий нуль) на 1, 2 или З, Проигравшим
считается тот, кто называет число 999.
![]() для заданного N необходимо определить,
может ли выиграть игрок, делающий первый ход, при наилучших
для заданного N необходимо определить,
может ли выиграть игрок, делающий первый ход, при наилучших ![]() последующих
ходах противника. Вывести сообщение «Первый выигрывает» или «Первый
проигрывает». В случае возможности выигрыша первым игроком требуется напечатать
все его возможные первые ходы.
последующих
ходах противника. Вывести сообщение «Первый выигрывает» или «Первый
проигрывает». В случае возможности выигрыша первым игроком требуется напечатать
все его возможные первые ходы.
4. Задан числовой треугольник из N строк. Написать программу, которая определяет максимальную сумму чисел, расположенных на пути, который начинается с верхнего числа и заканчивается на каком-нибудь числе в основании треугольника (максимум суммы среди всех таких путей).
7
2 7 7 4
На каждом шаге можно двигаться к соседнему по диагонали числу влево-вниз или вправо-вниз. Число строк в треугольнике больше и меньше либо равно 100. Все числа в треугольнике — целые в интервале между О и 99 включительно.
5. В магазине каждый товар имеет цену. Например, цена одного цветка равна 2, а цена одной вазы равна 5. Чтобы привлечь покупателей, магазин ввел скидки: решил продавать набор одинаковых или разных товаров по пониженной цене. Например: три цветка за 5 вместо 6 или две вазы вместе с одним цветком за 10 вместо 12.
Написать программу, вычисляющую наименьшую цену, которую покупатель должен заплатить за заданные покупки. Оптимальное решение должно быть получено посредством скидок. Набор товаров, который требуется купить, нельзя дополнять ничем, даже если бы это снизило общую стоимость набора. Для описанных выше цен и скидок наименьшая цена за три цветка и две вазы равна 14: две вазы и один цветок продаются по сниженной цене за 10 и два цветка — по обычной цене за 4.
![]() Входные данные содержатся в двух файлах:
INPUT.TXT и OFFER.TXT. Первый файл описывает покупки («корзину с покупками»),
второй — скидки. В обоих файлах содержатся только целые числа.
Входные данные содержатся в двух файлах:
INPUT.TXT и OFFER.TXT. Первый файл описывает покупки («корзину с покупками»),
второй — скидки. В обоих файлах содержатся только целые числа.
Первая строка файла INPUT.TXT содержит количество Ь различных
видов товара в корзине![]()
Каждая из следующих Ь строк содержит
значения К и р. Значение с — уникальный код товара (1![]()
Значение р задает, сколько единиц товара
находится в корзине (1 ![]() Обратите внимание, что общее количество
товаров в корзине может быть не более
Обратите внимание, что общее количество
товаров в корзине может быть не более ![]() (единиц).
(единиц).
Первая строка файла OFFER.TXT содержит количество s возможных
скидок (0<s <99). Каждая из следующих s строк описывает одну скидку,
определяя ![]() набор товаров и общую стоимость набора.
Первое число п в такой строке определяет количество различных видов товара в
наборе (1
набор товаров и общую стоимость набора.
Первое число п в такой строке определяет количество различных видов товара в
наборе (1 ![]() Следующие п лар чисел (с, К) указывают,
что К единиц товара с кодом с включены в набор для скидки (1
Следующие п лар чисел (с, К) указывают,
что К единиц товара с кодом с включены в набор для скидки (1 ![]() Последнее
число в строке р определяет уменьшенную стоимость набора (l
Последнее
число в строке р определяет уменьшенную стоимость набора (l ![]() Стоимость
набора меньше суммарной стоимости отдельных единиц товаров в наборе.
Стоимость
набора меньше суммарной стоимости отдельных единиц товаров в наборе.
Записать в выходной файл OUTPUT.TXT одну строку с наименьшей возможной суммарной стоимостью покупок, заданных во входном файле.
6. В файловой системе настенного персонального компьютера ВС-1 (Висячая Система) файлы организованы в каталоги. В компьютере нет понятия устройства и поэтому полное имя файла является строкой, состоящей из имен каталогов и имени файла, разделенных символом \, причем \ не может быть первым, последним символом, а также идти два раза подряд.
Имя файла (каталога) может быть произвольной длины, но длина полного имени файла не может быть длиннее N символов, В качестве символов, допустимых к употреблению в именах файлов (каталогов), могут использоваться символы из алфавита, состоящего из К букв (символ \ не входит в их число).
Для данных К (1 ![]() и
и ![]() определить
максимальное число файлов, которое можно записать на данный компьютер.
определить
максимальное число файлов, которое можно записать на данный компьютер.
7. Во
время трансляции концерта «Песня года» предприниматель К решил сделать бизнес
на производстве кассет. Он имеет М кассет с длительностью звучания D каждая и
хочет записать на них максимальное число песен. Эти песни (их общее количество
N) передаются в порядке 1, 2, N и имеют заранее известные ему длительности
звучания L (1), L (2) L (М). Предприниматель может выполнить одно из следующих
действий: записать очередную песню на кассету (если она туда ![]() помещается)
или пропустить ее; если песня на кассету не помещается, то может пропустить эту
песню или начать записывать ее на новую кассету, при этом старую кассету
отложить и туда уже ничего не записывать.
помещается)
или пропустить ее; если песня на кассету не помещается, то может пропустить эту
песню или начать записывать ее на новую кассету, при этом старую кассету
отложить и туда уже ничего не записывать.
Определить максимальное количество песен, которые предприниматель может записать на кассеты.
8. Учитель информатики живет на N-M этаже девятиэтажного дома с лифтом, который может останавливаться на каждом этаже. Между соседними этажами дома имеется лестница из двух пролетов, разделенных площадкой, по К ступенек в каждом пролете. Сколькими способами учитель может подняться на свой этаж, если, поднимаясь по лестнице, можно становиться на следующую ступеньку или идти через одну ступеньку?
9. Среди
всех ![]() двоичных чисел указать количество тех, у
которых в двоичной записи нет подряд идущих К единиц. Сами числа выдавать не
надо! N и К — натуральные,
двоичных чисел указать количество тех, у
которых в двоичной записи нет подряд идущих К единиц. Сами числа выдавать не
надо! N и К — натуральные, ![]()
10. В связи с о•гкрытием олимпиады по информатике N человек l0) решили устроить вечеринку. Для проведения вечеринки достаточно купить MF бутылок фанты, МВ бананов и МС тортов. Требуется определить минимальный взнос участника вечеринки.
При покупке определенных наборов товара действуют правила оптовой торговли: стоимость набора товара может отличаться от суммарной стоимости отдельн ых частей.
Написать программу, которая по входным данным определяет минимальный взнос участника вечеринки.
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ПОВЫШЕННОЙ
1. Вариант 1. Самое простое — это перебрать все возможные комбинации шести цифр и подсчитать число «счастливых» билетов.
Count: о; {количество «счастливых»
билетов} Гог а 1 :![]()
for а2: 0 to 9 do for аз: 0 to 9 do for а4: О to 9 do
Гот а5: 0
to 9 do Гот аб:![]()
![]() {«счастливый»?} then Count: =Count+ 1;
{«счастливый»?} then Count: =Count+ 1;
Под сложностью алгоритма будем понимать количество выполнений операторов наиболее глубоко вложенного цикла. Условие ii во вложенных циклах будет проверяться 106 раз, поэтому будем говорить, что сложность этого алгоритма 106.
Вариант 2. Обратим внимание на то, что в «счастли![]() вом»
билете последняя цифра аб однозначно определяется первыми пятью:
вом»
билете последняя цифра аб однозначно определяется первыми пятью:
06 = + а,..2 аз) — 05).
Если ![]() то билет «счастливый», иначе — нет
то билет «счастливый», иначе — нет ![]() Таким
образом, мы можем убрать шестой вложенный цикл:
Таким
образом, мы можем убрать шестой вложенный цикл:
Count : 0; Гог al:
![]() Гот а2:
Гот а2:
Гог аз:
for а5: 0 to 9 do
begin аб:![]()
if (аб> —0) and (аб< = 9) then = ![]() [ ; end;
[ ; end;
Сложность алгоритма 105 .
Используя зависимость ав от первых пяти цифр, мы уменьшили сложность алгоритма
и, вообще говоря, время выполнения программы ![]() в 10 раз!
в 10 раз!
Вариант З. Если комбинаций ар2аз первых трех цифр с суммой Т
-Ра2+аз насчитывается С [Т], то всего «счастливых» билетов с суммой половины Т
+ ![]() + аз = а4 а5 аб будет С [ ту.
+ аз = а4 а5 аб будет С [ ту.
Действительно, каждое «счастливое»
шестиразрядное число может быть получено «склейкой» двух произволь![]() ных
трехразрядных чисел с одинаковой суммой цифр. Всего существует 28 всевозможных
значений сумм Т— от О
ных
трехразрядных чисел с одинаковой суммой цифр. Всего существует 28 всевозможных
значений сумм Т— от О ![]() О до 27
О до 27 ![]() 9. ПОДС.ЧИТаеМ С
9. ПОДС.ЧИТаеМ С ![]()
![]() 27,
затем находим интересующее нас количество «счастливых» билетов: С [0]2 -F
С [112 4... + С [27]2.
27,
затем находим интересующее нас количество «счастливых» билетов: С [0]2 -F
С [112 4... + С [27]2.
Заметим, что «счастливых» билетов с суммой Т столько же, сколько и с суммой 27— Т. Действительно, если билет ща2аза4аьа6 с суммой Т— «счастливый», то таковым же является и билет (999999 — ща2аза4а5%) с суммой 27— Т. Поэтому число билетов можно вычислять и по формуле 2 (С [012 +... -FC [1312 ), т. е. рассматривать только суммы от 0 до 13.
var С: array [0..131 of longint;
(массив С из 14 элементов — по числу рассматриваемых сумм}
|
then с |
|
{нашли еще один билет} |
|
end; |
|
{с суммой Т) {считаем число билетов} |
|
Count: =Count+C |
|
С |
|
Count: |
|
{удваиваем сумму} |
![]() Count: —0;
Count: —0;
|
for Т: О to 13 do C [Tl: |
о; |
|
|
for а1 : |
|
[перебираем все) |
|
for а2: to 9 do f0T аз: О to 9 do begin
|
|
{возможные а 1 а2 аЗ} {если сумма не превышает 13, то} |
Сложность этого алгоритма равна 103.
Вариант 4. В варианте З мы перебирали комбинацию ![]() цифр
и искали количество комбинаций с суммами С [Т]. Сейчас мы пойдем от суммы Т, и
по ней будем определять, какое количество комбинаций ща2аз ее имеет. Итак, Т =
цифр
и искали количество комбинаций с суммами С [Т]. Сейчас мы пойдем от суммы Т, и
по ней будем определять, какое количество комбинаций ща2аз ее имеет. Итак, Т = ![]() аз.
аз.
![]() Минимальное значение, которое может
принимать щ, это тах {0, Т— 18}. Член Т— 18 появляется из следующих
соображений: пусть аз = 9, тогда —
Минимальное значение, которое может
принимать щ, это тах {0, Т— 18}. Член Т— 18 появляется из следующих
соображений: пусть аз = 9, тогда —
![]() Т— 18, но щ не может быть меньше 0.
Максимальное значение
Т— 18, но щ не может быть меньше 0.
Максимальное значение ![]() {9, Т} (так как а2 и аз неотрицательны,
{9, Т} (так как а2 и аз неотрицательны, ![]() то щ
К Т и одновременно щ <9).
то щ
К Т и одновременно щ <9).
Для цифры а2 аналогично получаем, что она лежит в пределах от тах {0, —9} до min {9, Т— ад.
Цифра аз по Т, al и ас) определяется однозначно. Получаем,
что комбинаций ща2аз с суммой Т и с первой цифрой а1 столько же, сколько
возможных цифр аж а именно min {9, ![]()
Как и в варианте З, мы можем рассматривать диапазон сумм от О до 13.
![]() Count:
Count:![]()
Гог Т •.=0 to 13 do begin
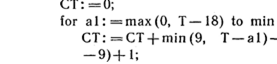 Т—al —
Т—al —Соипе. =Count+CT * СТ end;
Count: = Count * 2;
Сложность этого алгоритма (т. е. количество выполнений операций присваивания внутри двух вложенных циклов) есть 95 .
2. Задача имеет очевидное решение, которое состоит в
генерации всех ![]() чисел и проверке их на требуемое
свойство. Однако общее количество таких чисел равно 102N и поэтому
при потребуется очень много времени для получения результата даже на мощ
чисел и проверке их на требуемое
свойство. Однако общее количество таких чисел равно 102N и поэтому
при потребуется очень много времени для получения результата даже на мощ![]() ном
компьютере. Следовательно, необходимо разработать алгоритм, который не требует
генерации вс.ех чисел.
ном
компьютере. Следовательно, необходимо разработать алгоритм, который не требует
генерации вс.ех чисел.
Обозначим через S (К, i) количество К-разрядных чисел, сумма
цифр которых равна i. Например, S (2, ![]() —4, так как
существует 4 двуразрядных числа (03, 12, 21, 30), сумма цифр которых равна З.
Легко заметить, что S (l, i)—l при i<10 и S (l, при i>9. Предположим
теперь, что мы сумели вычислить значения величин S (М, i) для всех i от О до
9N, т. е. мы знаем, сколько существует
—4, так как
существует 4 двуразрядных числа (03, 12, 21, 30), сумма цифр которых равна З.
Легко заметить, что S (l, i)—l при i<10 и S (l, при i>9. Предположим
теперь, что мы сумели вычислить значения величин S (М, i) для всех i от О до
9N, т. е. мы знаем, сколько существует ![]() чисел с суммой цифр,
равной
чисел с суммой цифр,
равной ![]() 9N (9N — максимальная сумма цифр в
N-pa3рядном числе). Тогда нетрудно убедиться, что общее количество «счастливых»
2М-разрядных чисел равно
9N (9N — максимальная сумма цифр в
N-pa3рядном числе). Тогда нетрудно убедиться, что общее количество «счастливых»
2М-разрядных чисел равно ![]() l)2 +... +S ( ЛУ, 9N)2.
l)2 +... +S ( ЛУ, 9N)2.
Действительно, при решении задачи (вариант З) было показано,
что каждое «счастливое» ![]() число может быть получено «склейкой» двух
произвольных
число может быть получено «склейкой» двух
произвольных ![]() чисел с одинаковой суммой цифр.
чисел с одинаковой суммой цифр.
Таким образом, необходимо уметь вычислять значения величин S (К, i) для всех k<N, i<9k. Определим способ вычисления S (k-+- 1, i) через значения величин S (К, ј), j<i. Понятно, что любое (К + I )-разрядное число может быть получено из К-разрядного добавлением еще одного разряда (цифры). Следовательно,
![]()
где 1, 2, ... — возмо>кные добавленные
цифры. Ясно, что это О, 1, т, где ![]() (9, i). Следовательно,
(9, i). Следовательно,
![]()
З. Используем метод решения задачи 2.
![]() Обозначим искомое количество п-значных
чисел в десятичной системе счисления, у каждого из которых сумма цифр равна К,
через С (К, п). Последняя цифра числа может лежать в промежутке от 0 до 9. В
соответствии с этим сумма цифр (п— 1)-значного числа, получающаяся из
п-значного числа отбрасыванием последней цифры, может принимать одно из
значений К,
Обозначим искомое количество п-значных
чисел в десятичной системе счисления, у каждого из которых сумма цифр равна К,
через С (К, п). Последняя цифра числа может лежать в промежутке от 0 до 9. В
соответствии с этим сумма цифр (п— 1)-значного числа, получающаяся из
п-значного числа отбрасыванием последней цифры, может принимать одно из
значений К, ![]() К 9. Отсюда получаем, что
К 9. Отсюда получаем, что
![]()
Кроме того, С (К, l)—l при ![]() и С (К, при
и С (К, при
![]() 10.
10.
![]() 4. Очевидное решение задачи предполагает
разложение числа N—l на всевозможные суммы таким образом, чтобы каждое
слагаемое из суммы не превосходило К. Очевидно, что таких разложений очень
много, особенно если учитывать, что порядок слагаемых в разложении существенен,
так как он соответствует различной последовательности ходов фишки. Но обратим
внимание на то, что в условии задачи не требуется выписать все эти разложения,
необходимо только указать их общее количество!
4. Очевидное решение задачи предполагает
разложение числа N—l на всевозможные суммы таким образом, чтобы каждое
слагаемое из суммы не превосходило К. Очевидно, что таких разложений очень
много, особенно если учитывать, что порядок слагаемых в разложении существенен,
так как он соответствует различной последовательности ходов фишки. Но обратим
внимание на то, что в условии задачи не требуется выписать все эти разложения,
необходимо только указать их общее количество!
![]()
Таким образом, полагая ![]() и вычисляя
последовательно значения величин S (2), S(N) по опи
и вычисляя
последовательно значения величин S (2), S(N) по опи![]() санному выше правилу,
получаем значение S которое и указывает общее количество различных путей, по
которым фишка может пройти поле от начала до пози
санному выше правилу,
получаем значение S которое и указывает общее количество различных путей, по
которым фишка может пройти поле от начала до пози![]() ции с номером N.
ции с номером N.
5. Если покупатель отдаст все свои купюры продавцу, то понятно, что для решения исходной задачи необходимо найти размер минимальной сдачи, которую продавец не может вернуть, используя любые имеющиеся теперь у него купюры С, (его и покупателя). Для этого удобно отсортировать купюры по их достоинству в порядке неубывания.
Предположим, что продавец может вернуть любую сдачу от 1 до S, используя только первые i купюр. Для следующей (Н- 1)-й купюры достоинства Ci+l возможны 2 ситуации.
1) Ci+1<S-F2. Тогда понятно, что продавец может вернуть любую сдачу от 1 до Ci+ I -FS, так как любая из этих сумм представима либо первыми i купюрами, либо (i+ 1)-й купюрой вместе с некоторыми из первых i купюр.
2) Ci+1>S-Fl. В этом случае продавец не может вернуть сдачу S + 1.
Опишем алгоритм вычисления S.
![]()
кц
Если значение S не меньше суммарного количества денег покупателя,
то покупатель может купить товар любой доступной ему стоимости, точно
рассчитавшись за покупку. Иначе — Р— А 1 + -FAN![]()
6. Если S>Hl + + нп, то сумму выплатить нельзя. Если покупатель отдаст все свои купюры продавцу, то понятно, что для решения исходной задачи надо определить, может ли продавец вернуть сумму Н] + ... +
![]() + +Bm—S, используя любые имеющиеся теперь
у него купюры Mi (его и покупателя). Для этого удобно отсортировать купюры по
их достоинству в порядке неубывания.
+ +Bm—S, используя любые имеющиеся теперь
у него купюры Mi (его и покупателя). Для этого удобно отсортировать купюры по
их достоинству в порядке неубывания.
Пусть Р=М1+М2+... + Мп + т. Решим более общую задачу: найдем все непредставимые данными купюрами суммы на промежутке от 0 до Р.
Заведем массив А [О.. Р] натуральных чисел. Элемент ![]() —1,
если мы можем выплатить сумму i (т. е. существует набор купюр суммарного
достоинства Е), и А
—1,
если мы можем выплатить сумму i (т. е. существует набор купюр суммарного
достоинства Е), и А ![]()
![]() если выплатить не можем.
если выплатить не можем.
Будем строить всевозможные суммы, используя последовательно 0, 1, 2 N купюр.
Очевидно, что сумма из нуля купюр — это нуль, поэтому сначала А 1.
Предположим, что мы нашли всевозможные суммы, которые можно
составить, используя не более (К— 1) купюры М мк![]()
Добавим еще одну купюру Мк.
Теперь мы можем выплатить следующие суммы:
1)
все суммы, которые можно было составить с помощью купюр ![]() мк 1,
мк 1,
2) все суммы, которые можно было составить с помощью купюр Ml, . . . , Мк _1, увеличенные на Мк.
Расстановка новых пометок в массиве А может выглядеть следующим образом:
for i : = Р— М [К] downto 0 do
if A[il—1 then![]()
Мы проходим по массиву из конца в начало для того, чтобы не использовать повторно образованные на текущем шаге суммы.
После выполнения пф т шагов алгоритм заканчивает работу.
7. Очевидное решение задачи состоит в использовании процедуры, которая по заданным координатам (номеру строки i и номеру столбца / ) элемента определяет максимальное значение элементов, расположенных в нужной части матрицы А.
![]() Однако нетрудно заметить, что для элементов первого
столбца матрицы В справедливо соотношение
Однако нетрудно заметить, что для элементов первого
столбца матрицы В справедливо соотношение ![]() 1, N. Вычисление же
других столбцов можно проводить следующим образом:
1, N. Вычисление же
других столбцов можно проводить следующим образом:
При этом необходимо учитывать, что индексы элементов должны находиться в пределах границ массива.
8. Для решения пункта а) задачи достаточно воспользоваться
тем фактом, что для определения минимальной величины штрафа, взимаемого за
проход в клетку строки, достаточно знать минимальные величины штрафа,
взимаемого за проход в клетки (i— ![]() строки, которые являются соседними
рассматриваемой клетке. Поэтому алгоритм решения пункта
строки, которые являются соседними
рассматриваемой клетке. Поэтому алгоритм решения пункта
а) следующий: ![]()
нц для i от I до п Штраф Р, ![]() ll
ll
![]() кц для i от 2 до п
кц для i от 2 до п ![]() нц для ј от до т Штраф [i, jl: =
Штраф [i если и Штраф [i, то Штраф [i, jl: все если и Штраф [i, јКШтраф [i—
нц для ј от до т Штраф [i, jl: =
Штраф [i если и Штраф [i, то Штраф [i, jl: все если и Штраф [i, јКШтраф [i—![]()
то Штраф [i, jl: ![]() [i 1, j + ll+A [i,
[i 1, j + ll+A [i, ![]() все кц кц
все кц кц
9. а) Обозначим вершины М-угольника хо,
... , ![]() в порядке обхода по контуру. В дальнейшем
будем считать, что если в выкладках встреча-
в порядке обхода по контуру. В дальнейшем
будем считать, что если в выкладках встреча-
ется вершина с индексом К, то это то же, что и вершина с индексом К mod N (остаток от деления К на М).
Рассмотрим выпуклый ![]() вершинами которого
являются L последовательных вершин данного М-угольника, начиная с х и
заканчивая Xp+L_1 в порядке обхода по контуру. У этого 1) будем считать, что
отрезок [х • х ] — его диагональ.
вершинами которого
являются L последовательных вершин данного М-угольника, начиная с х и
заканчивая Xp+L_1 в порядке обхода по контуру. У этого 1) будем считать, что
отрезок [х • х ] — его диагональ.
![]()
Сумму диагоналей этой фигуры обозначим S (р, р +
![]()
Очевидно,
что по условию задачи: ![]()
S (p, S(p, ![]() (у точки и отрезка нет диагоналей);
(у точки и отрезка нет диагоналей);
![]()
S (р, ![]() (р, р+2) (здесь d(p, р-}-2)— длина
отрезка [хр; хр+2]).
(р, р+2) (здесь d(p, р-}-2)— длина
отрезка [хр; хр+2]).
![]() Предположим, что нам известно
S (р, p+L—l) для всех р
Предположим, что нам известно
S (р, p+L—l) для всех р![]() К.
К.
Найдем S (p, р + А).
Значения S(p, i) и S(i, К) были вычислены на предыдущих шагах; d (р, р+К) расстояние между вершинами Х И xp+k, — тоже можем вычислить.
Так как нас интересует минимальная сумма триангуляции (разбиения на треугольники), то мы ищем выражение (1) с минимальным значением:
![]()
![]() при
i=p+l, р-}-2 К—1.
при
i=p+l, р-}-2 К—1.![]()
![]() Находим S (p, p+h) для каждого р=О,
Находим S (p, p+h) для каждого р=О,![]()
MUHHMYM S (p, p+N—2) p=0, . N — l H macT HCKOMYTO TPmaHFYJIALIHK). LeÜCTBMTeJ1bHO, S (p, p4-N—-2) eCTb CTOHMOCTb pa36HBKH (burypbl nocene mp0BeneHHfl N —3 Anar0HaJ1eü.
6) AJIPOPHTM aHaJ10ruqeH a,nropHTMY c,nyqaq a), TOJ1bKO BMeCTO (#0PMYJ1b1 (2) Hamo HC110J1b30BaTb cJ1eAYK)11LYJo•.
S (p, ![]() max
(d (p, p+k), S (p, i), S (i, k)),
max
(d (p, p+k), S (p, i), S (i, k)),
me S (p, p+k) — AJIHHa
MaKCHMaJ1bHOÜ muaPOHaJIH ![]() B 4)Hrype C BePLUHHaMH XP +1,
B 4)Hrype C BePLUHHaMH XP +1, ![]() (0Tpe30K [xp, XP + k] cr-1HTaeTcH
AmarOHaJ1b10). Mbl 6epeM MHHHMYM no BCeM B03MOXHb1M pa36HBKaM (burypbl, a
CTOHMOCTb pa36HBKH orrpeÅe.nqeTcR KaK MaKCUMYM H3 AJIHHb1 muarOHaJIH d
(p, p+k) H ÄJIHH MaKCHMaJ1bHb1X zuaP0HaJ1eü S (p, i) H S (i, k).
(0Tpe30K [xp, XP + k] cr-1HTaeTcH
AmarOHaJ1b10). Mbl 6epeM MHHHMYM no BCeM B03MOXHb1M pa36HBKaM (burypbl, a
CTOHMOCTb pa36HBKH orrpeÅe.nqeTcR KaK MaKCUMYM H3 AJIHHb1 muarOHaJIH d
(p, p+k) H ÄJIHH MaKCHMaJ1bHb1X zuaP0HaJ1eü S (p, i) H S (i, k).
![]()
Meprom AHHaMHqeCKOPO nporpaMMHPOBaHHfl.
OnpeAeJIHM MaccHB d [O..m, O..n], 3J1eMeHTb1 KOToporo
FIOHflTHO,
I-ITO d [0, d [i,![]()
OqeBHAHb1M 06pa30M
nocnyqaeM d [i, ![]() [i, j 1]+ 1,
[i, j 1]+ 1,
Pij=l, eCJIH ai*bj, H Pij=0, eCJIH b}. B npaB0ü
B min COOTBeTCTByeT orrepaLIHH ymae]1eHHf1 CTPOKH al. ai_laj nocJ1eAHero 3J1ewteHTa ai, nocene qero 3a d [i— onepaLlHh CTPOKa al...ai_l npe06pa3yeTcH B CTPOKY bl...bj,
BTOPOMY 3J1ewreHTY — onepaLIHH BCTaBKH CHMBO,na bj B KO-
Hell CTPOKH bl...bi_l, 110J1yqeHHOÜ 3a d [i, j — l] onepauuü H3 CTPOKH al... a:, TpeTbeMY — KOHTeKCTHa% 3aMeHa ai Ha bf, 3aMeHa OCY1.ueCTBJIHeTCfl B cnyqae bi (Torma Pij= I)
и не происходит при совпадении а; и bi. Величина d [т, п] соответствует минимальному количеству операций, которые требуются для преобразований строки х в строку у. Алгоритм может быть записан так:
Гог to т do
Гот to п do
for to т do for to п do d [i, jl=min (d
[i—![]() 1, Ј — Pij);
1, Ј — Pij);
11. Пусть строка х состоит из цифр 0 и 1 и имеет длину М, а строка у (из символов А и В) — длину М.
Заведем матрицу А размера NXM, при этом строки матрицы помечаются цифрой строки х, а столбец — ј-м символом строки у.
Возьмем в качестве примера х— «00110», у = ![]() «ААААВВАА».
«ААААВВАА».
Первая цифра строки х (цифра 0) может быть преобразована в одну из последовательностей букв «А», «АА», «ААА», «АААА», являющихся префиксами строки у. Заносим символ «*» в те столбцы первой строки, буквы-пометки которых соответствуют последним буквам возможных последовательностей.
Таким образом, помечаются элементы А [1, 1], А [1, 2],
![]()
На каждом следующем шаге алгоритма будем преобразовывать очередную Ј-ю цифру строки х, которой соответствует строка матрицы А.
Находим «*» в предыдущей строке при просмотре ее слева
направо (этому столбцу соответствует последняя буква в какой-то из непустых
последовательностей букв, порожденных на предыдущем шаге). Если текущую циф![]() ру
можно преобразовать в последовательность букв, помечающих следующие за
найденным столбцы, то в этих столбцах в рассматриваемой строке ставим
ру
можно преобразовать в последовательность букв, помечающих следующие за
найденным столбцы, то в этих столбцах в рассматриваемой строке ставим![]()
Далее от места над последней помеченной ячейкой ищем в предыдущей строке и, когда находим, повто-
ряем указанные выше операции. Эти действия проводим далее для i=2, N. Вид матрицы после N шагов:

Если после N шагов в позиции (N, М) стоит х, то строки можно преобразовать друг в друга.
З а меч а н и е. Можно обойтись и одномерным массивом. В самом деле, при заполнении следующей строки мы обращаемся только к элементам предыдущей строки, к каждому — по одному разу.
12. Определим через F [i, минимальное число олераций, которое требуется для перемножения группы матриц с номерами от i до ј включительно.
Ясно, что F [i,![]()
Перемножение группы матриц с номерами от i до ![]() может
производиться различными способами, а именно, для некоторого выбранного К
сначала перемножаются наилучшим способом матрицы с номерами от i до К, затем
матрицы от (k-F 1)-й до ј-й, и, наконец, перемножаются получившиеся матрицы.
Понятно, что К может быть величиной от i до j—l. Учитывая требование получить
наилучший результат, величина F [i, ј] определяется как
может
производиться различными способами, а именно, для некоторого выбранного К
сначала перемножаются наилучшим способом матрицы с номерами от i до К, затем
матрицы от (k-F 1)-й до ј-й, и, наконец, перемножаются получившиеся матрицы.
Понятно, что К может быть величиной от i до j—l. Учитывая требование получить
наилучший результат, величина F [i, ј] определяется как
F
[i, тах (F [i, [К + 1, Л + п ![]() [К + 1]. т
[К + 1]. т![]()
где К может быть величиной от i до / — ![]() т
[Л определяют размеры матриц, получившихся ари перемножении в группах.
т
[Л определяют размеры матриц, получившихся ари перемножении в группах.
![]() нц для i от 1 до s
выполнять
нц для i от 1 до s
выполнять ![]() о;
о;
[К +
В ячейке F[l, s] после завершения работы алгоритма будет находиться искомое минимальное число операций.
Подумайте, каким образом можно в произведении матриц А1, 14 s расставить скобки так, чтобы они определяли оптимальный порядок умножения.
13. а) Рассмотрим сначала наиболее очевидный, но, как это
обычно бывает, наименее эффективный (очень медленный) алгоритм. Будем
генерировать все подпоследовательности данной ![]() последовательности и
для каждой из подпоследовательностей проверять, является ли она строго возрастающей
и максимальной по длине.
последовательности и
для каждой из подпоследовательностей проверять, является ли она строго возрастающей
и максимальной по длине.
Будем генерировать числа от 0 до У— 1, находить их двоичное представление и формировать подпоследовательность из элементов массива А с индексами, соответствующими единичным битам в этом представлении.
Всего существует У таких подпоследовательностей, поэтому даже при небольших п результата придется ждать очень долго.
22l
Предположим, что при генерации подпоследовательностей мы нашли К-элементную строго возрастающую подпоследовательность. В дальнейшем имеет смысл рассматривать только подпоследовательности, состоящие из более чем К элементов (подумайте почему).
Рассмотрим исходную п-элементную последовательность. Если она не является искомой, то будем генерировать (N 1)-элементные подпоследовательности. Если и среди них не найдено решение, то будем рассматривать подпоследовательности из (N—2) элементов и т. д.
В худшем случае (каком?) придется анализировать порядка У вариантов.
для более быстрого решения этой задачи можно применить
дихотомию по К — количеству элементов в подпоследовательности (как?![]()
Рассмотрим другое, более эффективное решение этой задачи. Заведем массивы А, В и С длины N: массив А [1..N1 используется для хранения чисел исходной последовательности; элемент B[i] — значение длины максимальной возрастающей подпоследовательности, последний элемент которой А [i]; величина С [i] есть индекс элемента, предшествующего элементу А [ij в этой максимальной подпоследовательности (А если предшествующего элемента нет).
Если N== 1, то А [1] и есть искомая подпоследовательность.
При этом В 1, ![]() Предположим, что мы заполнили массивы В
и С от начала и до элемента г— 1. Попытаемся получить элементы В [i] и C[i].
Для этого будем просматривать массив А от 1 до (i—
Предположим, что мы заполнили массивы В
и С от начала и до элемента г— 1. Попытаемся получить элементы В [i] и C[i].
Для этого будем просматривать массив А от 1 до (i— ![]() элемента и искать
такой индекс К, для которого одновре
элемента и искать
такой индекс К, для которого одновре![]() менно выполняются следующие условия:
менно выполняются следующие условия:
1) А [КК АШ,
2) В [К] максимально.
Очевидно, что максимальную по длине подпоследовательность,
заканчивающуюся элементом А [i], можно по![]() лучить, приписав этот
элемент к максимальной подпос-
лучить, приписав этот
элемент к максимальной подпос-
![]()
ледовательности с последним элементом А [К]. Следовательно, В [k]+ l и C[i]=k.
Пусть мы обработали все N элементов массива А и нашли максимальный элемент массива В. Пусть это элемент с индексом IndexMax. По построению это длина максимальной подпоследовательности.
Получить искомую подпоследовательность
можно следующим образом. Пусть — индекс текущего эле![]() мента
подпоследовательности, распечатываемой с конца. Сначала полагаем ј: =IndexMax и
печатаем элемент А [ј], который является последним. Предшествующий ему в
последовательности элемент имеет индекс С
мента
подпоследовательности, распечатываемой с конца. Сначала полагаем ј: =IndexMax и
печатаем элемент А [ј], который является последним. Предшествующий ему в
последовательности элемент имеет индекс С ![]() поэтому индекс следующего
с конца элемента определяется как / : —С [Л. Описанные действия повторяем пока
поэтому индекс следующего
с конца элемента определяется как / : —С [Л. Описанные действия повторяем пока ![]() не
станет равным О (т. е. пока не дойдем до начала последовательности).
не
станет равным О (т. е. пока не дойдем до начала последовательности).
Запись алгоритма на языке Pascal:
![]() for 1
for 1
—1; IndexMax: —![]()
Гот 1 =2 to N do for К:
![]() if (А 1)
then begin
if (А 1)
then begin
 if В begin
if В begin
Мах:![]()
IndexMax: ![]() end; end;
end; end; ![]() Ј: —— IndexMax;
Ј: —— IndexMax; ![]() while
while ![]() do begin writeln (А [jl);
do begin writeln (А [jl);
![]()
![]() end;
end;
![]() В программе
переменная Мах используется для хранения длины текущей максимальной
подпоследователь
В программе
переменная Мах используется для хранения длины текущей максимальной
подпоследователь![]() ности.
ности.
![]() В этой задаче элемент массива С [i]
содержит ссылку
В этой задаче элемент массива С [i]
содержит ссылку ![]() на элемент, предшествующий А [i] в
подпоследовательности максимальной длины. Такая ссылочная структура
на элемент, предшествующий А [i] в
подпоследовательности максимальной длины. Такая ссылочная структура ![]() данных
называется однонаправленным списком. Если у элемента есть ссылка как на
предыдущий, так и на последующий элемент, то список — двунаправленный (его
можно реализовать, если использовать не один массив ссылок, а два).
данных
называется однонаправленным списком. Если у элемента есть ссылка как на
предыдущий, так и на последующий элемент, то список — двунаправленный (его
можно реализовать, если использовать не один массив ссылок, а два).
В рассмотренной задаче оптимальные значения хранятся в
массиве В.![]()
Получить более эффективное решение можно, если на каждом шаге
хранить не все полученные ранее оптимальные значения и соответствующие
подпоследовательности, а только наиболее перспективные из них. ![]()
Пусть k(L, i) обозначает множество
возрастающих подпоследовательностей длины L, которые составлены из элементов с
номерами от I до i— 1. Из двух подпоследовательностей длины L более
перспективной будет та, у которой величина последнего элемента меньше, так ![]() как
ее может продолжить большее число элементов. Пусть SP (L, i) — самая
перспективная подпоследовательность длины L (с минимальным по величине
последним элементом), а S (i) — множество всех подпоследовательностей SP (L, i)
при всевозможных L. В S (i) содержится не более i— I подпоследовательностей (с
длинами
как
ее может продолжить большее число элементов. Пусть SP (L, i) — самая
перспективная подпоследовательность длины L (с минимальным по величине
последним элементом), а S (i) — множество всех подпоследовательностей SP (L, i)
при всевозможных L. В S (i) содержится не более i— I подпоследовательностей (с
длинами ![]() i— 1).
i— 1).
Пусть мы знаем S (i). Для того чтобы определить, какие
подпоследовательности может продолжать элемент последовательности А, достаточно
знать последние элементы перспективных подпоследовательностей длины ![]() N,
индексы которых будут храниться в массиве Ind.
N,
индексы которых будут храниться в массиве Ind.![]()
Последний элемент перспективной подпоследовательности длины р строго меньше последнего элемента перс-
![]()
пективной подпоследовательности длины р-н (объясните почему). Поэтому элемент должен продолжить подпоследовательность максимальной длины, последний элемент которой меньше элемента.
Учитывая упорядоченность последних элементов перспективных подпоследовательностей, поиск можно сделать методом половинного деления (дихотомией), используя массив Ind.
При присоединении элемента к такой подпоследовательности длины р ее длина увеличивается на 1, а последним элементом становится А [i]. При этом множество S(i+l) совпадает с S (i), за исключением подпоследовательности SP (р+ 1, i+ 1), полученной добавлением элемента к подпоследовательности SP (р, i). При хранении подпоследовательности для каждого элемента удобно хранить номер предшествующего ему элемента.
б) Для каждого индекса i найдем
подпоследовательность максимальной длины с разрывом в А [П. Будем искать
максимальную по длине подпоследо![]() вательность, заканчивающуюся в элементе А
вательность, заканчивающуюся в элементе А
![]() и максимальную по длине
подпоследовательность, начинающуюся в нем (для этого будем просматривать массив
А не слева направо, а справа налево). в) Заведем массив C [0..m+l, l..N]. В нем
строка будет хранить информацию о последовательностях
и максимальную по длине
подпоследовательность, начинающуюся в нем (для этого будем просматривать массив
А не слева направо, а справа налево). в) Заведем массив C [0..m+l, l..N]. В нем
строка будет хранить информацию о последовательностях ![]() I разрывом (нулевая
строка — фиктивная); /-й элемент в этой строке есть длина самой длинной
подпоследовательности элементов «хвоста» массива А (от ј-го элемента до п-го),
начинающейся в ј-й позиции и имеющей не более i—l разрывов. Алгоритм:
I разрывом (нулевая
строка — фиктивная); /-й элемент в этой строке есть длина самой длинной
подпоследовательности элементов «хвоста» массива А (от ј-го элемента до п-го),
начинающейся в ј-й позиции и имеющей не более i—l разрывов. Алгоритм:
1. Заполнить нулевую строку нулями (чтобы можно было заполнить первую строку по общему алгоритму).
2. Для каждой строки i от I до т +1 выполнить следующие действия:
8 Информатика. 8—9 кл.
2.1. Для ј-го элемента массива А (ј изменяется от N до 1) найти максимальную по длине подпоследовательность, которую можно присоединить к этому элементу так, чтобы получить подпоследовательность максимальной длины с не более чем i—l разрывом. Для этого:
2.1.1. найти элемент А [К]
последовательности А, ![]() больший А [ј] и стоящий в массиве А правее
ј-го элемента и с максимальным С [Ј, К];
больший А [ј] и стоящий в массиве А правее
ј-го элемента и с максимальным С [Ј, К];
2.1.2. просмотреть элементы (Ј— строки матрицы С, начиная с (ј + 1)-го и до конца; найти максимальный из них, пусть это
![]() s ] с C[i, К], больший из них (обозначим
его С [гош, col]), увеличенный на 1, запомнить в C[i, ј]; это и будет длина
максимальной подпоследовательности, начинающейся в позиции ј, с не более чем i—
s ] с C[i, К], больший из них (обозначим
его С [гош, col]), увеличенный на 1, запомнить в C[i, ј]; это и будет длина
максимальной подпоследовательности, начинающейся в позиции ј, с не более чем i—
![]() рывом;
рывом;
2.1.4. запомнить индексы гош и col элемента массива С, предшествующего С [i, ј], как элементы X[i, ј] и Y[i, ј] соответственно.
После окончания цикла максимальный элемент ![]() 1)-й строки
матрицы С и есть максимальная длина возрастающей подпоследовательности с т
разрывами. Выписать всю подпоследовательность в обратном порядке можно
следующим образом: для каждого элемента подпоследовательности в массивах Х и У
хранится информация о предшественнике. Мы, начиная с максимального элемента
1)-й строки матрицы С, восстанавливаем всю подпоследовательность.
1)-й строки
матрицы С и есть максимальная длина возрастающей подпоследовательности с т
разрывами. Выписать всю подпоследовательность в обратном порядке можно
следующим образом: для каждого элемента подпоследовательности в массивах Х и У
хранится информация о предшественнике. Мы, начиная с максимального элемента
1)-й строки матрицы С, восстанавливаем всю подпоследовательность.
Обоснование алгоритма.
Пусть известны C[i— 1, ј] для всех ј от до N и для некоторого г, а также C[i, К] для К от ј-1- 1 до N. Мы хотим вычислить C[i, П.
Для ј-го элемента массива А существует максималь-
ная по длине подпоследовательность с не
более чем ![]() I разрывом, начинающаяся с А [ј]. Второй
элемент (обозначим его А [К]) этой максимальной подпоследовательности (если он,
конечно, есть) может быть:
I разрывом, начинающаяся с А [ј]. Второй
элемент (обозначим его А [К]) этой максимальной подпоследовательности (если он,
конечно, есть) может быть:
![]() 1) больше А [ј]; тогда находим его среди
элементов, обладающих следующими свойствами:
1) больше А [ј]; тогда находим его среди
элементов, обладающих следующими свойствами:
![]()
б) С [i, К] максимальный (т. е. мы присоединяем к А [ј]
максимальную по длине подпоследователь![]() ность с не более чем i— l разрывом, фор
ность с не более чем i— l разрывом, фор![]() мируя
подпоследовательность опять не более чем
мируя
подпоследовательность опять не более чем ![]() 1 разрывом);
1 разрывом);
2) меньше или равный А [ј]; тогда ищем его среди элементов, обладающих следующими свойствами:
—1, К] максимальнь1й (т. е. присоединяем максимальную подпоследовательность с не более чем i—2 разрывами, формируя подпоследовательность с не более чем i—1 разрывом).
Полученная подпоследовательность имеет максимальную длину, так как длина подпоследовательности, которая начинается с А [КЈ, — максимальна. Упоминавшиеся выше индексы гош и col, которые запоминаются в Х [Ј, ј] и У [Ј, ј] соответственно, обозначают следующее: col — индекс следующего за А [ј] элемента в максимальной по длине подпослецовательности, начинающейся в позиции ј и имеющей не более i— l разрывов; row— — максимальное количество разрывов в подпоследовательности, начинающейся в А [col].
![]() 14. Для решения задачи элементы массива
удобно упорядочить по абсолютной величине (в порядке неубывания). Если в массиве
есть элементы, равные 0, то один
14. Для решения задачи элементы массива
удобно упорядочить по абсолютной величине (в порядке неубывания). Если в массиве
есть элементы, равные 0, то один ![]() из них и будет последним элементом искомой
последовательности, поэтому их можно игнорировать. Пусть КЈ обозначает
максимальное количество элементов, которое может находиться в некоторой
последовательности с требуемым свойством, последним элементом которой является
г-й элемент.
из них и будет последним элементом искомой
последовательности, поэтому их можно игнорировать. Пусть КЈ обозначает
максимальное количество элементов, которое может находиться в некоторой
последовательности с требуемым свойством, последним элементом которой является
г-й элемент.
Понятно, что наименьшему по абсолютной величине элементу не может предшествовать ни один элемент, поэтому Кр=О, где р — индекс первого ненулевого элемента.
Для каждого следующего элемента с номером ј, j—p+ l, N,
необходимо определить максимальное количество элементов, которое может
предшествовать рассматриваемому элементу, с учетом требуемого свойства.
Понятно, что это количество есть максимум из величин К К Кр , где элементы с
номерами Р], П, ![]() рт, р являются делителями элемента с
номером i. Поэтому мы имеем рекуррентную формулу для вычисления ki.
рт, р являются делителями элемента с
номером i. Поэтому мы имеем рекуррентную формулу для вычисления ki.
![]() Крт)+
Крт)+![]()
Значение Км, вычисленное по описанному выше правилу, и определяет максимальное количество элементов, которое может находиться в некоторой последовательности с требуемым свойством (без учета возможного нуля в конце последовательности).
![]() Для того чтобы установить, какие элементы образуют
максимальную последовательность, достаточно для каждого номера ј помнить тот
номер из Р), Р2, . р т, на котором достигается максимум для чисел Крр К К . Эти
номера можно определять параллельно с вычислением значения К(ј) в некотором
массиве, например ПРЕДОК. Используя эту информацию, легкоу определить номера
элементов последовательности, проходя от элемента i с максимальным значением К,
к элементу, который ему предшествует (ПРЕДОК (i)), до тех пор, пока не придем к
первому элементу последовательности (ПРЕДОК
Для того чтобы установить, какие элементы образуют
максимальную последовательность, достаточно для каждого номера ј помнить тот
номер из Р), Р2, . р т, на котором достигается максимум для чисел Крр К К . Эти
номера можно определять параллельно с вычислением значения К(ј) в некотором
массиве, например ПРЕДОК. Используя эту информацию, легкоу определить номера
элементов последовательности, проходя от элемента i с максимальным значением К,
к элементу, который ему предшествует (ПРЕДОК (i)), до тех пор, пока не придем к
первому элементу последовательности (ПРЕДОК![]()
15. Очевидно, что параллелепипеды можно повернуть так, чтобы размеры ребер каждого параллелепипеда шли в неубывающем порядке. Зафиксируем этот поря-
![]() док. Вложение параллелепипеда В в
параллелепипед С возможно только тогда, когда для двух параллелепипедов В (Ь
(1)с (п)) выполняются неравенства Ь
док. Вложение параллелепипеда В в
параллелепипед С возможно только тогда, когда для двух параллелепипедов В (Ь
(1)с (п)) выполняются неравенства Ь
16. Метод решения этой задачи аналогичен использованному при решении задачи о нахождении максимальной по длине возрастающей подпоследовательности.
Пусть а, Ь, с натуральные числа.
Будем рассматривать только случай • так как в случае
задача неразрешима, а в случае сразу получаем, что и ![]()
Обозначим через L множество делителей числа а, лежащих на отрезке [Ь, с]. Количество всех делителей числа а не превышает 2 Е (если а = / • д, то f<N'7, фа, всего разных может быть не более а, столько же и разных д). Пусть Ll — минимальный элемент из L, а Ь — максимальный. Пусть в массиве S [l..p] первый элемент равен единице, а все остальные — делители числа а, не меньшие Ь, записанные в порядке возрастания. Из утверждения следует, что р<а+2.
Будем искать минимальнуто по длине подпоследовательность элементов массива S, которая начинается единицей, заканчивается а, каждый элемент которой делится на предыдущий, причем частное принадлежит множеству L.
В случае, если а, Ь, с, х [i] целые, в массив S помещаем в
порядке возрастания модуля все делители числа а, начиная с минимального
элемента в L. Далее ![]() аналогично.
аналогично.
17. Задачу можно переформулировать следующим образом.
Последовательность из п вагонов, занумерованных от 1 до п, необходимо разбить на не более чем т подпоследовательностей, в каждой из которых номера вагонов возрастают.
Одним из самых простых алгоритмов сортировки вагонов является алгоритм, основывающийся на следующем правиле.
1)
Помещаем очередной вагон (номер которого К) ![]() на путь с минимально
возможным номером, при условии, что последний вагон, стоящий на этом пути,
имеет номер меньше К.
на путь с минимально
возможным номером, при условии, что последний вагон, стоящий на этом пути,
имеет номер меньше К.
2)
Если все вагоны состава будут таким образом ![]() расположены на
станции, то, очевидно, что вагон N9 на каком-то пути будет самым правым и его
можно подать на выход. Затем вагон NQ 2 также может быть подан на выход, так
как не может стоять на пути за вагоном с номером, большим 2,
расположены на
станции, то, очевидно, что вагон N9 на каком-то пути будет самым правым и его
можно подать на выход. Затем вагон NQ 2 также может быть подан на выход, так
как не может стоять на пути за вагоном с номером, большим 2,
З) Если же какой-то вагон нельзя поместить ни на один путь на станции, то это значит, что все пути «перекрыты» вагонами с большими номерами, причем последние вагоны на этих путях расположены в порядке убывания. Вместе с последним вагоном, не нашедшим себе места, эти т вагонов в исходной последовательности составляют убывающую подпоследовательность длины т + 1.
![]() Отметим, что если можно отсортировать последовательность
вагонов, то можно отсортировать также и любую их подпоследовательность, и
наоборот. Поэтому из существования убывающей подпоследовательности длины т-}-1
следует, что исходную последовательность отсортировать нельзя.
Отметим, что если можно отсортировать последовательность
вагонов, то можно отсортировать также и любую их подпоследовательность, и
наоборот. Поэтому из существования убывающей подпоследовательности длины т-}-1
следует, что исходную последовательность отсортировать нельзя.
18. Можно, конечно, число А умножить само на себя п— 1 раз, но для этого надо выполнить п— 1 операцию умножения. Рассмотрим метод, требующий меньшего числа умножений (он, однако, не всегда дает минимальное число умножений).
Если п — четное (п=2т), то будем ВЫЧИСЛЯТЬ А П , используя тождество
![]() Таким образом, возведение А в степень будет выглядеть
следующим образом:
Таким образом, возведение А в степень будет выглядеть
следующим образом:
![]()
и вычисление требует 5 операций умножения.
![]() П р и м е ч а н и е. Используя данный
метод, для возведения числа в степень п потребуется порядка logp операций
умножения.
П р и м е ч а н и е. Используя данный
метод, для возведения числа в степень п потребуется порядка logp операций
умножения. ![]()
Программа на языке Pascal может выглядеть так:
![]()
![]() А, N: integer; function power (N: integer): integer; begin if then
if odd (N) tnen {N нечетно?} power: =SQR (power(N div 2)) * А else power:
=SQR (power (N div 2)) else power: = А end; begin read (А, N); writeln (power
(N)); end;
А, N: integer; function power (N: integer): integer; begin if then
if odd (N) tnen {N нечетно?} power: =SQR (power(N div 2)) * А else power:
=SQR (power (N div 2)) else power: = А end; begin read (А, N); writeln (power
(N)); end;
![]()
![]()
![]() Можно ту же самую идею реализовать и по-другому (далее мы
приводим выдержку из книги Д. Кнута «Искусство программирования для ЭВМ», т. 2,
с. 482):
Можно ту же самую идею реализовать и по-другому (далее мы
приводим выдержку из книги Д. Кнута «Искусство программирования для ЭВМ», т. 2,
с. 482):
«Запишем п в двоичной системе счисления и заменим в этой записи каждую цифру парой букв SX, а каждую цифру О — буквой S, после чего вычеркнем крайнюю левую пару букв SX. Результат, читаемый слева направо, превращается в правило вычисления х“, если букву S интерпретировать как операцию возведения в квадрат, а букву Х— как операцию умножения на х.
Например, если 11=23, то его двоичным представлением будет
10111; строим последовательность SX S SX SX SX, удаляем из нее начальную пару
SX и в итоге получаем следующее правило вычисления: S SX SX SX. Согласно этому
правилу, мы должны «возвести х в квадрат, затем снова возвести в квадрат, затем
умножить на х, возвести в квадрат, умножить на х, возвести в квадрат и, наконец,
умножить на х»; при этом мы последовательНО вычисляем Х2, Х4,
Х5, Х! , x ll , Х ![]() , Х23
, Х23![]()
Этот «бинарный метод» легко обосновать, рассмотрев последовательность получаемых в ходе вычисления показателей: если S интепретировать как операцию умножения на 2, а Х— как операцию прибавления и если начать с 1, а не с х, то наше правило дает нам в соответствии со свойствами двоичной системы счисления число п».
Приведенный метод не дает минимального числа операций умножения. Для вычисления х23 нам, по изложенному выше методу, потребуется 7 операций умножения. В действительности, их необходимо только 6:
![]() 23
23
Алгоритм нахождения минимального числа операций (кроме
полного перебора) сейчас неизвестен. ![]()
19.
![]()
![]()
![]() Пусть 2 — массив из N элементов, у — из М. Положим и ] 1.
Берем элемент z [i] и ищем минимальное К, такое, что у z[i] (мы находим
очередной совпадающий символ в строках и у). Полагаем г: =i+l и / :
Пусть 2 — массив из N элементов, у — из М. Положим и ] 1.
Берем элемент z [i] и ищем минимальное К, такое, что у z[i] (мы находим
очередной совпадающий символ в строках и у). Полагаем г: =i+l и / : ![]() Повторяем
поиск элемента z [i] в оставшейся части последовательности у. Условия окончания
поиска:
Повторяем
поиск элемента z [i] в оставшейся части последовательности у. Условия окончания
поиска:
а) если i стало больше N (т. е. все элементы массива z являются подпоследовательностью элементов у), тогда можно получить вычеркиванием элементов из у;
б) если в оставшейся части
последовательности у не найдено элемента, совпада ющего с очередным 2 ![]() то
2 из у получить нельзя.
то
2 из у получить нельзя.
20.
Пусть х![]()
Заведем матрицу А [О,.т, О..п]. Элемент А [i, / ] будет длиной максимальной общей подпоследовательности
(Xl, ..., Xi) и ( щ, ..., у». Сначала А
[i, [0, i=0, ![]() п.
п.
Пусть =уј, тогда требуется увеличить длину максимальной общей
подпоследовательности![]()
![]() Уј 1) на 1:
Уј 1) на 1:
В случае, если
![]() А [Е, ј]— тах {А [i
но так как всегда А [i
А [Е, ј]— тах {А [i
но так как всегда А [i
А [Ј,
Величина А [т, п] и дает длину максимальной общей
подпоследовательности. Найдем саму подпоследовательность. Пусть А [т, Двигаясь
по последней строке справа налево, ищем самый левый элемент в этой строке со
значением d. Двигаемся от него вверх по столбцу в поиске элемента столбца с
минимальным первым индексом и значением d. Пусть это А [i, ј]. Тогда элемент ![]() 1]
равен d— l, а хј и у, — это последние общие совпадающие элементы в х и у.
1]
равен d— l, а хј и у, — это последние общие совпадающие элементы в х и у.
Начиная от элемента А [i— l ј— 1], повторяем, как было описано выше, движение влево и вверх по матрице, находим предпоследний совпадающий элемент в х и у и
Программа: ![]()
![]() for to т do A [i,
О]: о; for Ј: О to п do А [0, ј]: О;
for to т do A [i,
О]: о; for Ј: О to п do А [0, ј]: О; ![]() for to т do Гог Ј:
for to т do Гог Ј:
if
![]() d: =A[m,
п]; i: т• ј: =п; while(d< do begin while A[i, Ј while A[i— l,
write ('Элемент последовательности номер', d, 'есть', x[i]);
d: =A[m,
п]; i: т• ј: =п; while(d< do begin while A[i, Ј while A[i— l,
write ('Элемент последовательности номер', d, 'есть', x[i]);
![]() {переход к поиску предшествую-}
{переход к поиску предшествую-}
{щего элемента в последовательности} end;
21. В последовательностях х и у избавляемся от незначащих нулей. Если хоть одна из последовательностей стала пустой, то 2=0. Если последовательности не пустые, то крайние левые цифры и в х, и в у равны 1. Для полученных последовательностей используем алгоритм задачи 20 (для получения максимального z необходимо, чтобы старшая цифра была I и двоичная запись г имела максимальную длину), но при этом для каждого А [i, ј] — длины последовательности, необходимо хранить добавочно и саму последовательность; при присвоении значения А [Ј, ј] одновременно будем запоминать и последовательность максимальной длины. Если таких несколько, то берем из них последовательность с максимальным значением. Поэтому алгоритм задачи 20 запишется следующим образом.
Пусть S [О.. т, О.. п] — массив строк. В S [Ј, ј] будет храниться подпоследовательность, длина которой А [Ј, ј].
for to т do A[i, 01: —О; for Ј : —О
to п do А[Ј' О]: ![]() for to т do f01 Ј • •• —0 to п do
for to т do f01 Ј • •• —0 to п do
![]()
![]() for to т do for Ј : to п do begin if
for to т do for Ј : to п do begin if ![]() then begin
then begin
lil; end;
A[i, ј]: (А
[i,![]() 1,
1, ![]()
![]() Ј]: —тах ( S [i,
Ј]: —тах ( S [i,![]() 1,
1, ![]() end; write(A [т, nl, '— длина',
end; write(A [т, nl, '— длина',![]()
Глава 5. ЗАДАЧИ КОМБИНАТОРИКИ
С задачами, в которых приходится выбирать те или иные
предметы, располагать их в определенном порядке ![]() и отыскивать среди
всевозможных расположений наилучшее, люди сталкиваются постоянно. Например,
начальник цеха распределяет несколько видов работ между имеющимися станками,
агроном размещает посевы сельскохозяйственных культур на нескольких полях,
завуч школы составляет расписание уроков. При решении такого вида задач
возникли понятия об упорядочении и группировании объектов. С этими понятиями и
работает наука комбинаторика.
и отыскивать среди
всевозможных расположений наилучшее, люди сталкиваются постоянно. Например,
начальник цеха распределяет несколько видов работ между имеющимися станками,
агроном размещает посевы сельскохозяйственных культур на нескольких полях,
завуч школы составляет расписание уроков. При решении такого вида задач
возникли понятия об упорядочении и группировании объектов. С этими понятиями и
работает наука комбинаторика.
![]()
![]() Комбинаторика — это область математики, в которой
изучаются вопросы о том, сколько различных комбина
Комбинаторика — это область математики, в которой
изучаются вопросы о том, сколько различных комбина![]() ций, подчиненных тем
или иным условиям, можно составить из заданных объектов.
ций, подчиненных тем
или иным условиям, можно составить из заданных объектов.
Иногда количество вариантов, которые надо проанализировать при решении комбинаторной задачи, очень велико. В этом случае единственной возможностью получения результата за допустимое время, а не через столетия, является использование компьютера.
Как и любая другая наука, комбинаторика имеет свою терминологию. Основным понятием комбинаторики является комбинаторный объект, или соединение. При выборе т элементов из п различных элементов принято говорить, что они образуют соединение из п элементов по т.
В зависимости от того, имеет ли значение порядок элементов в соединении или нет, а также от того, входят в соединение все п элементов или только часть их, различают три вида соединений. Это — перестановки, размещения и сочетания.
S 1. СОЕДИНЕНИЯ
1.1. Перестановки
Соединения, каждое из которых содержит п различных элементов, взятых в определенном порядке, называются перестановками из п элементов. Следует отметить, что порядок элементов в перестановке существенен и в образовании перестановки участвуют все п элементов
![]()
Пример. Выпишем все перестановки из элементов
![]()
abc, ась, Ьас, Ьса, саЬ, cba.
![]() Количество всех способов, которыми можно
переставить п различных предметов, расположенных на п различных местах, принято
обозначать Рп (читается «число перестановок из п»).
Количество всех способов, которыми можно
переставить п различных предметов, расположенных на п различных местах, принято
обозначать Рп (читается «число перестановок из п»).
Найдем Рп. На первое из имеющихся п мест предмет может быть
выбран п способами, на второе место — (п— —1) способом, на третье место — (п—
2) способами и т. д. На предпоследнее место предмет выбирается из двух
оставшихся, а для последнего места выбор предмета единственен. Общее количество
способов будет равно произведению п (п— ![]() . 2 . l. Такое
произведение называется факториалом числа п и обозначается п! Таким образом,
Рп=п!
. 2 . l. Такое
произведение называется факториалом числа п и обозначается п! Таким образом,
Рп=п!
Прим ер. Сколько всего шестизначных четных чисел можно составить из цифр 1, З, 4, 5, 7 и 9, если в каждом из этих чисел ни одна цифра не повторяётся?
Последняя цифра четного числа должна быть четной, поэтому в
данном случае последней цифрой числа может быть только цифра 4. Оставшиеся пять
цифр могут стоять на оставшихся пяти местах в любом порядке. Поэтому количество
способов их расстановки равно ![]()
![]() 5!— 120.
5!— 120.
Иногда требуется не просто подсчитать количество перестановок из п элементов, но и найти каждую из них.
Существует несколько алгоритмов генерации всех перестановок из п элементов. Они различаются порядком получения перестановок.
Рассмотрим один из хорошо известных алгоритмов, в процессе
исполнения которого перестановки п чисел располагаются лексикографически (в
словарном порядке). Это значит, что перестановки сравниваются слева направо
поэлементно и большей из них является та, у которой раньше встретился элемент,
больший соответ![]() ствующего ему элемента во второй
перестановке. (Например, если 5, 4, 6, 7), а 5, 6, 4, 7), то S<L, так как
S3<L3.)
ствующего ему элемента во второй
перестановке. (Например, если 5, 4, 6, 7), а 5, 6, 4, 7), то S<L, так как
S3<L3.)
Опишем алгоритм для п=5, отчего рассуждения не утратят общности. В дальнейшем, для удобства, будем работать не с самими элементами, а с их номерами (от до п).
![]() Принцип работы алгоритма разъясним на примере. Допустим,
необходимо воспроизвести все перестановки чисел 1, 2, З, 4, 5. Первой
перестановкой считаем перестановку (1, 2, З, 4, 5). Последней перестановкой
будет (5, 4, З, 2, 1). Элементы перестановки будем хранить в массиве.
Принцип работы алгоритма разъясним на примере. Допустим,
необходимо воспроизвести все перестановки чисел 1, 2, З, 4, 5. Первой
перестановкой считаем перестановку (1, 2, З, 4, 5). Последней перестановкой
будет (5, 4, З, 2, 1). Элементы перестановки будем хранить в массиве.
Предположим, что на некотором шаге работы алгоритма получена перестановка Р:
Р=(З, 4, 5, 2, Р2, рз, Р4, П).
Для того чтобы определить непосредственно следующую за ней перестановку, необходимо выполнить шаги:
Шаг 1. Будем просматривать данную перестановку справа налево
и следить за тем, чтобы каждый следующий элемент перестановки (элемент массива
с большим номером) был больше предыдущего (т. е. элемента массива с меньшим
номером), и остановимся сразу же, как только это правило нарушится ![]() а
5>4). Место остановки указано подчеркиванием:
а
5>4). Место остановки указано подчеркиванием:
![]()
Шаг 2. Затем вновь просматриваем пройденный путь (справа налево) до тех пор, пока не дойдем до первого числа, которое уже больше отмеченного. Место второй остановки отмечено двойным подчеркиванием.
![]()
Шаг З. Поменяем местами отмеченные числа:
![]()
Шаг 4. В части массива, расположенной справа от двойного
подчеркивания, отсортируем все числа в порядке возрастания. Так как до сих пор
они были упорядочены по убыванию, то это легко сделать, записав в обратном
порядке указанную часть массива. Получим новую перестановку, которую обозначим ![]() ф,
ф, ф, к):
ф,
ф, ф, к):
![]()
Это и есть та перестановка, которая непосредственно следует за Р в лексикографическом порядке.
Примеча ни е. Действительно, P<Q, так как Т—4, [72 = 5.
Пусть существует такая перестановка R, что ![]() Тогда р,
Тогда р,![]()
![]() По построению q2 — наименьшее число в
множестве {l, 2, 4, 5) (это множество содержит элементы перестановки Q без и),
такое, что ф>р2. Поэтому для r2 верно одно из двух равенств: или ф. Но так
как в Р элементы, начиная с рз, убывают, то из следует, что если ре=Г2, то P=R.
Аналогично, так как в Q элементы, начиная с К, возрастают, то из следует, что
если r2=q2, то и R=Q. Следовательно, перестановки R не существует.
По построению q2 — наименьшее число в
множестве {l, 2, 4, 5) (это множество содержит элементы перестановки Q без и),
такое, что ф>р2. Поэтому для r2 верно одно из двух равенств: или ф. Но так
как в Р элементы, начиная с рз, убывают, то из следует, что если ре=Г2, то P=R.
Аналогично, так как в Q элементы, начиная с К, возрастают, то из следует, что
если r2=q2, то и R=Q. Следовательно, перестановки R не существует.
В массиве Р будем хранить номера элементов. Вначале в массиве хранятся числа от 1 до п, расположенные в порядке возрастания так, что каждый элемент равен своему номеру. Нулевой элемент фиктивный, он используется для проверки окончания работы. Генерация перестановок будет закончена, когда нулевой элемент станет отличным от нуля.
Запишем алгоритм генерации перестановок:
нц для i от О до п
нц пока Р [0l=o
![]() :вывод
очередной переста-
:вывод
очередной переста-
:новки на экран
: поиск (справа налево)
: большего предшествую-
:щего ему (ШАГ 1)
: поиск числа, большего
:отмеченного (ШАГ 2)
: перестановка двух чисел,
:найденных выше (ШАГ З)
: запись части массива в
:обратном порядке
: во вспомогательный мас![]() :сив г
:сив г
:перенос элементов из мас-
исходный массив
Вопросы для повторения
1. Что такое перестановки?
2. Чему равно число перестановок из 4 элементов? из 6 элементов?
З. Как сгенерировать все перестановки из а элементов а лексикографическом порядке?
4. Укажите перестановку, лексикографически следующую за
![]()
1.2. Сочетания
Соединения, отличающиеся друг от друга, по крайней мере, одним элементом, каждое из которых содержит т элементов, взятых из п различных элементов, называются сочетаниями (комбинациями или выборками) из п элементов по т. Порядок следования элементов не учитывается.
При м ер. Выпишем все сочетания из элементов а, Ь, с по два:
ab, ас, bc.
Количество способов, которыми можно выбрать т элементов из п, принято обозначать С (п, т) или С? (читается «число сочетаний из п по т»). Значение величины С (п, т) вычисляется по формуле
п!
![]() (Доказательство
формулы будет приведено ниже.) Отметим, что
(Доказательство
формулы будет приведено ниже.) Отметим, что
Прим ер. Сколькими способами можно из 10 человек выбрать команду для игры в городки? Команда состоит из 4 человек.
Количество. способов равно числу сочетаний из 10 по 4.
C(10, 4)![]() —210,
—210,![]()
Для решения некоторых задач требуется не только подсчитать
число сочетаний, но и найти каждое из них. Приведем алгоритм генерации всех
сочетаний из п эле![]() ментов по т. Так же, как и в алгоритме
генерации перестановок, будем работать не с самими элементами, а с их номерами
1, 2, п.
ментов по т. Так же, как и в алгоритме
генерации перестановок, будем работать не с самими элементами, а с их номерами
1, 2, п.
Так как порядок элементов в сочетании не учитывается, то
получать сочетания удобно в порядке возрастания индексов используемых на данном
шаге элементов (общее их число есть т). Текущее сочетание будем хранить в
массиве В. В качестве начальной конфигурации возьмем следующую: (1, 2, т), для
которой ![]() 1 т. Сочетания будем получать в
возрастающем лексикографическом порядке, поэтому последним сочетанием будет
(п—т+ 1, п—т+2,
1 т. Сочетания будем получать в
возрастающем лексикографическом порядке, поэтому последним сочетанием будет
(п—т+ 1, п—т+2,![]()
Для каждого элемента последнего сочетания
выполняется условие В ![]() Для всех остальных сочетаний это
равенство будет нарушено хотя бы для одного элемента.
Для всех остальных сочетаний это
равенство будет нарушено хотя бы для одного элемента.
Для генерации очередного сочетания найдем элемент В [ј] с максимальным индексом ј, такой, что выполняется неравенство
![]()
При этом будем просматривать текущее сочугание справа налево.
Затем увеличим это В [ј] на 1, а для всех ![]() полагаем В
полагаем В ![]() Если
такого В [ј] не существует, то генерация сочетаний длины т закончена.
Если
такого В [ј] не существует, то генерация сочетаний длины т закончена.
нц для от 1 до т
B[il: —![]() : инициализация массива
: инициализация массива
Ј : 100;
![]() :вывод очередного
полу: ченного сочетания
:вывод очередного
полу: ченного сочетания
![]() п + ј —т) : поиск
элемен: та, удовлетво: ряющего усло-
п + ј —т) : поиск
элемен: та, удовлетво: ряющего усло-
9 Информатика, кл. 241
![]() : проверка окончания
гене-
: проверка окончания
гене-
: рации сочетаний
: изменение элемента, удов-
:летворяющего условию ( * )
= В [К— l]+l : изменение элементов, стоя-
: щих после элемента, удов:летворяющего условию ( * )
кц
Вопросы для повторения
1. Что называется сочетанием из п элементов по т?
2. Чему равно число сочетаний из 5 по З? из 6 по 2?
З. Как сгенерировать все сочетания из 5 элементов по 2?
4. Какое сочетание будет получено алгоритмом (5.2) вслед за (З, 5, 8), если п— 8, т = З?
1.3*. Размещения
Соединения, отличающиеся друг от друга составом элементов или их порядком, каждое из которых содержит т (т<п) элементов, взятых из п различных элементов, называются размещениями из п элементов по т. П р им е р. Выпишем все размещения из элементов а, Ь, с по два:
ab, ba, ас, са, bc, cb.
Количество способов, которыми можно выбрать и разместить по т различным местам т и п различных элементов, принято обозначать А (п, т) или Апт (читается «число размещений из п по т»). Вычислим значение величины А? , т. е. вычислим, сколькими способами можно выбрать и разместить по т различным местам т из п различных предметов.
На первое место можно поместить любой из п пред![]() метов, на
второе место — любой предмет из (п— 1) оставшихся, на третье — один из (п— 2)
оставшихся и т. д. На предпоследнее место с номером (т— 1) — любой из
оставшихся п—(т—2) предметов, а на последнее т-е место —
метов, на
второе место — любой предмет из (п— 1) оставшихся, на третье — один из (п— 2)
оставшихся и т. д. На предпоследнее место с номером (т— 1) — любой из
оставшихся п—(т—2) предметов, а на последнее т-е место — 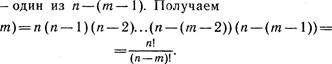 один из 1).
Получаем
один из 1).
Получаем
По определению, 0! = 1.
Пр и мер. Сколько всего семизначных телефонных номеров, в каждом из которых ни одна цифра не повторяется?
Эта задача о выборе и размещении по семи различным местам семи из десяти различных цифр, поэтому число указанных телефонных номеров равно
А (10, 7)— 10-9-8-7-6-5-4=604 800.
А теперь докажем формулу (1) п. l.2 для числа сочетаний.
Выбрать т из п различных предметов можно С(п, т) способами, и в каждом из выбранных сочетаний имеется т! возможностей упорядочить т предметов этого сочетания. Поэтому имеется т! С (п, т) возможностей выбрать и разместить по т разным местам т из п разных предметов, т. е.
![]()
Отсюда следует, что число сочетаний из п различных предметов по т в т! раз меньше, чем числа размещений из п по т, т. е.
![]()
![]() В том случае, если
требуется сгенерировать все раз
В том случае, если
требуется сгенерировать все раз![]() мещения из п по т, то для каждого
сочетания, полученного алгоритмом (5.2), применяют алгоритм генерации
перестановок (5.1). (Этот алгоритм разработайте самостоятельно.)
мещения из п по т, то для каждого
сочетания, полученного алгоритмом (5.2), применяют алгоритм генерации
перестановок (5.1). (Этот алгоритм разработайте самостоятельно.)
243
Вопросы для повторения
1. Что называется размещениями из п
элементов по т? ![]()
2. Чему равно число размещений из 5 по
З? из 6 по 2? ![]()
З. Как сгенерировать все размещения из 5 элементов по 2?
S СОЕДИНЕНИЯ С ПОВТОРЕНИЯМИ
2.1. Размещения с повторениями
До сих пор рассматривались соединения, в каждое из которых любой из п различных элементов входит один раз. Можно рассматривать соединения с повторениями, т. е. соединения, в каждом из которых любой из п различных элементов может входить более одного раза.
Размещения из п элементов, в каждое из которых входит т элементов, причем один и тот же элемент может повторяться в каждом размещении любое число раз, но не более чем т, называются размещениями из п элементов по т с повторениями.
П ример. Выпишем размещения с повторениями из двух элементов а, Ь по три:
ааа, aab, aba, abb, Ьаа, bab, bba, bbb.
Количество размещений из п элементов по т с повторениями обозначают Апт (п). Справедлива формула Апт пт .
Действительно, на каждое из т мест мы можем поместить любой из п элементов.
Пр им е р. Каждый телефонный номер состоит из 7 цифр. Сколько всего телефонных номеров, содержащих только цифры 2, З, 5, 7?
Эта задача о числе размещений в семи позициях семи цифр, каждая из которых может быть 2, З, 5 или 7. Цифры в телефонном номере могут повторяться.
Число всех указанных номеров есть 141 ![]()
![]() 16
384.
16
384.
Опишем алгоритм генерации всех размещений из п элементов по т с повторениями. Пронумеруем элементы от 0 до (п— 1) и в дальнейшем будем работать не с самими элементами, а с их номерами. Каждому размещению мы можем сопоставить число в п-ичной системе счисления, состоящее из т цифр. И наоборот, каждому из таких чисел соответствует одно-единственное размещение. Минимальным из таких чисел будет число, состоящее из т нулей. Для получения всех чисел, соответствующих размещениям, будем каждый раз прибавлять по 1 к текущему числу, пока не получим число из и т нулей. Данное число не соответствует ни одному из искомых размещений, а является указателем того, что генерация закончена (предыдущим числом было число, состоящее из т цифр, каждая из которых равнялась п— 1). Приведем фрагмент программы, генерирующей размещения с повторениями.
нц для i от 0 до т
![]() 0 : начальное число, состоя щее из : всех
нулей кц
0 : начальное число, состоя щее из : всех
нулей кц
к младшему
![]() : разряду и (А [т 1=0)
: разряду и (А [т 1=0)
: перенос I в следуюиций
: разряд
: вывод очередного размещения с
: повторениями
кц
![]() 2.2. Перестановки с повторениями
2.2. Перестановки с повторениями![]()
Перестановки из п предметов, в каждую из которых входят
одинаковых предметов одного типа, ![]() одинаковых предметов другого типа и т. д.
до пк одинаковых предметов К-го типа, где + пН-... + 14 = п, называются
перестановками из п элементов с повторениями.
одинаковых предметов другого типа и т. д.
до пк одинаковых предметов К-го типа, где + пН-... + 14 = п, называются
перестановками из п элементов с повторениями.
П р и м ер. Получим перестановки из двух элементов а и Ь, каждый из которых взят по два раза.
aabb, abab, abba, baab, baba, bbaa.
Число всех таких перестановок с повторениями принято обозначать Рп (щ, 112, . . . , пк). Оно может быть найдено по формуле
Рп(П1, П![]() (3)
(3)
Возьмем некоторую перестановку из числа Рп (щ, щ, ![]() пк)
всех перестановок с повторениями. В ней все возможные перестановки элементов
первого типа, считая их разными, можно осуществить 111! способами, затем все
возможные перестановки элементов второго типа, считая их разными, можно
осуществить 112! способами и т. д., а затем все возможные перестановки
элементов К-го типа, считая их разными, можно осуществить пк! способами.
Осуществляя все возможные перестановки только элементов каждого типа, получим
пк)
всех перестановок с повторениями. В ней все возможные перестановки элементов
первого типа, считая их разными, можно осуществить 111! способами, затем все
возможные перестановки элементов второго типа, считая их разными, можно
осуществить 112! способами и т. д., а затем все возможные перестановки
элементов К-го типа, считая их разными, можно осуществить пк! способами.
Осуществляя все возможные перестановки только элементов каждого типа, получим ![]() перестановок,
которые бы возникли из взятой перестановки с повторениями, если бы имелась
возможность как-то различать входящие в каждый тип одинаковые элементы.
Проделав это для каждой перестановки с повторениями, получим п! число
всевозможных перестановок из п различных предметов.
перестановок,
которые бы возникли из взятой перестановки с повторениями, если бы имелась
возможность как-то различать входящие в каждый тип одинаковые элементы.
Проделав это для каждой перестановки с повторениями, получим п! число
всевозможных перестановок из п различных предметов.
Таким образом, ![]() РП (щ, п,2, . . . ,
РП (щ, п,2, . . . , ![]() откуда
следует формула для числа перестановок с повторениями.
откуда
следует формула для числа перестановок с повторениями.
Для получения всех перестановок с повторениями можно
воспользоваться алгоритмом (5.1), заменив в нем знаки > на (Почему?)![]()
2.3. Сочетания с повторениями
Сочетаниями из п элементов по т, с повторениями называются соединения, содержащие т элементов (без учета порядка следования), причем любой элемент может входить в соединение некоторое число раз, не большее т.
Пример. Получим сочетания из элементов а, Ь по три с повторениями:
ааа, aab, abb, bbb.
Число всех сочетаний из п элементов по т с повторениями принято обозначать С? (п). Оно может быть найдено по формуле:
Для доказательства этой формулы закодируем каждое сочетание с
повторением с помощью нулей и единиц. Сначала напишем столько единиц, сколько
взято элементов первого типа. Потом, чтобы отделить элементы первого типа от
элементов второго типа, запишем нуль, а затем — столько единиц, сколько взято
элементов второго типа. Далее снова напишем нуль (если не было взято ни одного
элемента второго типа, но в записи появятся два следующих друг за другом нуля).
Далее напишем столько единиц, сколько взято элементов третьего типа, снова
напишем нуль и т. д., пока не будут ![]() выписаны единицы, соответствующие
элементам п-го типа.
выписаны единицы, соответствующие
элементам п-го типа.
Для сочетания ааа из приведенного выше примера запись будет lllO, а для abb 1011.
Таким образом, число различных сочетаний из п элементов по т с повторениями равно числу перестановок с повторениями, которые можно составить из т единиц и (п 1) нулей. Для вычисления количества перестановок с повторениями применим формулу (З). Общее количество нулей и единиц равно
![]()
При м ер. В кондитерском магазине продавались четыре сорта пирожных. Сколькими способами можно купить семь пирожных?
Эта задача о числе сочетаний из 4 элементов по 7 с повторениями:
с74(п) — 120. 7!3!
Доказательство формулы (4) дает алгоритм генерации всех сочетаний из п элементов по т с повторениями. Для этого применим алгоритм (5.2) для генерации сочетаний из т+п— I элемента по п— 1 (или по т, что одно и то же, см. формулу (2)).
В массиве В (см. алгоритм (5.2)) хранятся в порядке возрастания индексы используемых на данном шаге элементов. Количество таких индексов в случае генерации сочетаний из (т -4- п— 1) элемента по (n— l) есть (п— 1). Каждый из индексов показывает позицию нуля в перестановке с повторениями, составленной из т единиц и (п— 1)нулей. Количество единиц между соседними нулями (а также количество единиц до первого нуля и после последнего) дает количество элементов каждого типа.
Пример. Пусть на каком-то шаге генерации для п=4, ![]() —8,
п I —3) в массиве В получен следующий набор индексов: 1, З, 6. Этот набор дает
конфигурацию 010l 1011, т. е. элемент первого типа в данную выборку не входит,
элемент в ггорого типа входит раз, элемент третьего типа — 2 раза,
элемент четвертого типа —2 раза.
—8,
п I —3) в массиве В получен следующий набор индексов: 1, З, 6. Этот набор дает
конфигурацию 010l 1011, т. е. элемент первого типа в данную выборку не входит,
элемент в ггорого типа входит раз, элемент третьего типа — 2 раза,
элемент четвертого типа —2 раза.
Для генерации сочетаний с повторениями можно воспользоваться и алгоритмом генерации перестановок с повторениями.
S ПОДМНОЖЕСТВА
Пусть имеется некий набор из п различных элементов, обладающих некоторым общим свойством. Совокупность этих элементов называют множеством. Общее свойство элементов множества обычно содержится в самом названии (задании) каждого множества. Множества обычно обозначают заглавными латинскими буквами.
При меры множеств: множество цифр, множество букв некоторого алфавита, множество точек плоскости, множество звезд во Вселенной.
Если каждый элемент множества А является элементом множества В, то множество А называется подмножеством множества В. Любая совокупность элементов из данного множества образует подмножество данного множества.
Подмножество, не содержащее ни одного элемента, называют пустым. Пустое множество является подмножеством всякого множества.
Пр и меры.
1) Множество всех положительных четных чисел является подмножеством множества всех натуральных чисел.
2)
Выпишем все подмножества множества, состоящего из элементов а, Ь, с.
Каждое подмножество будем заключать в фигурные скобки (пустое подмножество
обозначают![]()
Количество всех подмножеств п-элементного множества равно (23 =8).
![]() Пусть задано множество из п элементов.
Пронумеруем элементы данного множества от 0 до (п— 1). В дальнейшем будем
работать не с самими элементами, а с их номерами.
Пусть задано множество из п элементов.
Пронумеруем элементы данного множества от 0 до (п— 1). В дальнейшем будем
работать не с самими элементами, а с их номерами.
Для генерации подмножеств создадим массив В [О..п] из 1)
элемента (п-й элемент фиктивный и используется для определения окончания
работы). В если ![]() элемент в подмножество не входит, и В [i]
1, если входит. Таким образом, пустому подмножеству будет соответствовать набор
из п нулей, а п-элементному подмножеству — набор из п единиц. Тут явно заметна
связь представления подмножества с двоичным представлением числа.
элемент в подмножество не входит, и В [i]
1, если входит. Таким образом, пустому подмножеству будет соответствовать набор
из п нулей, а п-элементному подмножеству — набор из п единиц. Тут явно заметна
связь представления подмножества с двоичным представлением числа.
Будем генерировать числа от 0 до У— 1, находить их двоичное представление и формировать подмножество из элементов исходного множества с индексами, соответствующими единицам в этом представлении.
![]()
![]()
![]()
![]()
![]() Вначале определим В для всех i от 0 до п,
что соответствует пустому подмножеству. Будем рассматривать массив В как запись
двоичного числа В , . В [0] и моделировать операцию сложения этого числа с
единицей. При сложении будем просматривать число справа налево, заменяя единицы
нулями до тех пор, пока не найдем нуль, в который занесем 1. Генерация
подмножеств заканчивается, как только В (предыдущая конфигурация была 1..
Вначале определим В для всех i от 0 до п,
что соответствует пустому подмножеству. Будем рассматривать массив В как запись
двоичного числа В , . В [0] и моделировать операцию сложения этого числа с
единицей. При сложении будем просматривать число справа налево, заменяя единицы
нулями до тех пор, пока не найдем нуль, в который занесем 1. Генерация
подмножеств заканчивается, как только В (предыдущая конфигурация была 1..![]()
Приведем фрагмент программы генерации всех подмножеств:
нц пока В [пј=0
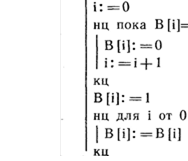
кц
S 4. РЕАЛИЗАЦИЯ ПЕРЕБОРА ВАРИАНТОВ.
![]() СОКРАЩЕНИЕ ПЕРЕБОРА
СОКРАЩЕНИЕ ПЕРЕБОРА
Часто встречаются задачи такого рода, когда трудно найти решение, отличное от полного перебора всех возможных вариантов.
Алгоритмы, рассмотренные выше, позволяют организовать основные типы перебора.
Примеры переборных задач.
1. Получить все способы расстановки шести книг разных авторов.
Для решения задачи применяется алгоритм генерации всех перестановок из шести элементов.
2. Для участия в конкурсе требуется выбрать трех человек из класса в 20 человек.
Для решения задачи используется алгоритм генерации всех с.очетаний из 20 элементов по З.
З. Получить все четырехзначные числа, у которых все цифры нечетные.
Для решения задачи применяется алгоритм генерации всех размещений из пяти элементов по четыре с повторениями.
4. Из семи красных и восьми белых роз требуется составить букет из пяти роз. Перечислите все возможные варианты.
Для решения задачи применяется алгоритм генерации всех сочетаний из двух по пять с повторениями. Количество рассматриваемых вариантов при переборе может быть очень большим, что влечет за собой большие временные затраты. В некоторых случаях количество рассматриваемых вариантов удается сократить, используя определенные свойства задачи. К сожалению, не существует общих рекомендаций как это сделать. В каждой конкретной задаче приходится искать свой способ.
Проиллюстрируем сокращение перебора на примере следующих задач:
Задача 1. Часы
В матрице размера 3Х3 расположены 9 циферблатов с заданным положением стрелок (рис. 31). Требуется установить на всех циферблатах время 12 часов.
Возможно 9 различных способов изменения стрелок на циферблатах. Каждый такой способ задается набором циферблатов (рис. 32), стрелки которых поворачиваются на 90 0 по часовой стрелке. На рисунке для каждого из способов соответствующие циферблаты выделены серым цветом, каждый способ определяется номером — числом от до 9.
Перевод стрелок из начального состояния в конечное
производится последовательностью шагов. За один шаг можно осуществить перевод
стрелок на циферблатах ![]() одним из указанных способов.
одним из указанных способов.
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
Рис. 31 Рис. 32
соседних преобразования в последовательности можно поменять местами, при этом окончательный результат при последовательном выполнении преобразований не изменится. При этом количество одинаковых преобразований в оптимальной (наиболее короткой) последовательности не превосходит З, так как последовательное применение 4 одинаковых преобразований переводит циферблаты в исходное состояние.
Таким образом, если рассмотреть все возможные допустимые минимальные последовательности преобразований, в которых каждое из преобразований может выполняться от 0 до З раз (т. е. рассмотреть все возможные 9-разрядные числа в четверичной системе счисления, когда каждый разряд отражает количество выполнений соответствующего преобразования), то можно найти среди них решение поставленной задачи. Это соответствует генерации всех размещений из 4 элементов по 9 с повторениями. Число таких последовательностей равно 49 .
Однако можно существенно сократить количество рассматриваемых последовательностей, если проанализировать влияние каждого из преобразований на конкретный циферблат. В следующей таблице приведены множества преобразований, влияющих на каждый из циферблатов.
|
Номер циферблата |
Номера преобразований, влияющих на циферблат |
|
1 2 з 4 5 6 7 8 9 |
|
![]() Итак, на циферблат влияют преобразования
l, 2 и 4. Попытаемся установить его в конечное положение, выполняя
последовательно все возможные комбинации преобразований 1, 2 и 4. При этом
любой произвольный набор комбинаций преобразований 1 и 2 (в количестве al и щ,
соответственно) однозначно определяет количество преобразований, которое
необходимо для установления циферблата I в конечное положение. Таким образом,
Итак, на циферблат влияют преобразования
l, 2 и 4. Попытаемся установить его в конечное положение, выполняя
последовательно все возможные комбинации преобразований 1, 2 и 4. При этом
любой произвольный набор комбинаций преобразований 1 и 2 (в количестве al и щ,
соответственно) однозначно определяет количество преобразований, которое
необходимо для установления циферблата I в конечное положение. Таким образом, ![]() фиксировано
для заданных значений al и щ. Из второй строчки таблицы видно, что теперь
достаточно рассмотреть только всевозможные значения аз (при уже фиксированных
значениях ar и а2), при этом значение аб будет фиксировано. Из строчки З
следует, что аб фиксировано, из строчки 4 — что фиксировано 07, из строчки 5
фиксировано
для заданных значений al и щ. Из второй строчки таблицы видно, что теперь
достаточно рассмотреть только всевозможные значения аз (при уже фиксированных
значениях ar и а2), при этом значение аб будет фиксировано. Из строчки З
следует, что аб фиксировано, из строчки 4 — что фиксировано 07, из строчки 5 ![]() строчки
7 — ф.
строчки
7 — ф.
Таким образом, достаточно осуществить перебор по возможным значениям 01, а2 и Щ, вычисляя при этом значения аз, ао ф, щ, ад. При этом полученная последовательность должна переводить циферблаты в конечное состояние.
![]() Итак, нам достаточно перебрать 43 комбинаций,
что значительно меньше, чем 4 9.
Итак, нам достаточно перебрать 43 комбинаций,
что значительно меньше, чем 4 9.
Задача 2. Раздел наследства
Баронесса фон Бирлингхофен оставила после себя двум дочерям ларец с золотыми монетами. Ее завещание гласило, что все золото получит соседний монастырь, если дочерям не удастся разделить содержимое ларца на две равные части. Достоинство каждой золотой монеты является целым числом.
![]() П р и мер. Если монеты в ларце были
достоинством 2, 10, 4, З, 7, 4, то их можно разделить между наследницами
следующим образом: l0, З, 2 и 7, 4, 4. Если же золотые монеты были достоинством
1, 9, 7, З, 8, то раздел наследства невозможен, и оно достанется монастырю.
П р и мер. Если монеты в ларце были
достоинством 2, 10, 4, З, 7, 4, то их можно разделить между наследницами
следующим образом: l0, З, 2 и 7, 4, 4. Если же золотые монеты были достоинством
1, 9, 7, З, 8, то раздел наследства невозможен, и оно достанется монастырю.
Программа должна вводить количество монет N и их достоинства
а2, ...я ам. Результатом работы программы должно быть сообщение: «раздел
наследства невоз![]() можен» или «раздел наследства возможен». В
последнем случае необходимо указать, монеты какого достоинства получит каждая
из наследниц.
можен» или «раздел наследства возможен». В
последнем случае необходимо указать, монеты какого достоинства получит каждая
из наследниц.
Обозначим сумму номиналов всех монет через S. Это число должно быть четным, иначе раздел невозможен.
Для решения данной задачи можно, например, применить алгоритм
(5.4) для генерации всех подмножеств множества монет и поиска среди этих
подмножеств такого, стоимость которого равна S / 2. Под стоимостью подмножества
будем понимать суммарную стоимость номиналов монет, входящих в данное
подмножество. Количество подмножеств равно, как уже отмечалось., 2 ![]() Попытаемся
сократить количество рассматриваемых подмножеств, исходя из следующих
соображений:
Попытаемся
сократить количество рассматриваемых подмножеств, исходя из следующих
соображений:
1)
2) Если уже сгенерировано некоторое подмножество А со стоимостью больше S/2, то добавление любых элементов к этому подмножеству не сможет привести к решению и, следовательно, генерировать их не имеет смысла.
З) Максимальная по номинальной стоимости монета (пусть это монета си) должна попасть к одной из наследниц, поэтому раздел наследства начнем с этой монеты. Из-за того, что стоимость выбранной монеты максимальна, разность между S/2 и стоимостью этой монеты минимальна, что, возможно, приведет к уменьшению количества рассматриваемых вариантов. С этой же целью отсортируем монеты в порядке невозрастания их номиналов.
4) Если одна из монет имеет номинал, равный половине искомой суммы, то разбиение найдено.
5) Если хоть одна монета имеет номинал более половины искомой суммы, то разбиение невозможно.
IlYHKTb1 4 H 5 AOCTaTO LIHO npogepHTb TOJ%KO MOHeTbi C MaKCHMaJ1bHb1M HOMHHaJIOM.
B MaCCHBe A 6YAeM XPaHHTb HOMHHaJ1b1 MOHeT. B MacCHBe st B HqeVfKax C UHÅeKcaMU 0T 1 AO st [0] xpaHHTch H0Mepa Bb16paHHb1X ceüqac MOHeT (B OTCOPTHPOBaHHOM MaccHBe). MOHeTb1 C 3THMH HOMepaMH 06pa3YT0T IIOÅMHOxeCTBO CTOHMOCTU S. B MaCCHBe rez [IOMeCTViM Te MOHeTbl, KOTOPb1e flOJIYMHT OAHa H3 HaCJ1eAHHU, Torna npyraq nony-
![]() OCTaBLUmeCh MOHeTbf.
OCTaBLUmeCh MOHeTbf.
9TH paccyxaeHHR HBJ1flK)TCfl OCHOBOi c.nenyrouxero avnroPHTMa:
summa : —0
![]()
Hil : HaXOÅHM CTOHMOCTb summa : = summa a [il : HaCJ1eACTBa
: COPTHPOBKa![]()
: MaccHBa
: C HCXOAHb1MH maHHb1MU
: B flOPflÅKe y6b1BaHHfl
![]() :
KOJInqeCTBO Bb16paHHb1X ceüqac MOHeT
:
KOJInqeCTBO Bb16paHHb1X ceüqac MOHeT
: HHAeKC MOHeTb1 C MaKCHMaJ1bHb1M : HOMHHaJIOM
: H0Mep oqepeAH0i A06aBJ1qervf0Ü MO: HeTb1

: переходим к следующей монете
![]() : если решение не найдено, то возвращаемся на
: если решение не найдено, то возвращаемся на
: т. е. выбрасываем последнюю добавленную монету
: удаление последней
: добавленной
: монеты из выбранных
все
Рассмотрим работу данного алгоритма на приведенном выше примере. После сортировки массива имеем:
![]()
surnma = 15; s=
lO•, st—![]()
Выпишем значения переменных при каждом прохождении цикла ПОКА.
|
Значение переменной i |
Значение переменной s |
Массив st |
|
2 |
|
|
|
З |
|
|
|
4 |
|
|
|
5 |
|
|
|
6 |
|
1, з, о, о, о, ор |
![]()
1 Элемент st хоть и присутствует в массиве, но в дальнейшем рассмотрении не участвует, так как количество элементов равно
![]()
|
Значение переменной i |
Значение переменной |
|
Массив st |
|
|
4 |
|
|
|
|
|
5 |
|
st— |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
![]()
![]() Метод, использованный для решения
данной задачи, называется перебором с возвратом или бектрекингом
(Backtraching).
Метод, использованный для решения
данной задачи, называется перебором с возвратом или бектрекингом
(Backtraching).
Некоторые задачи, являющиеся на первый взгляд переборными, могут быть решены другими методами.
Задача З. «Счастливые» билеты
Если бы в задаче требовалось не только подсчитать количество «счастливых» билетов, но и выдать номера этих билетов, то в этом случае необходимо было бы использовать только переборный метод.
На примере этой задачи видна разница между подсчетом количества вариантов, удовлетворяющих условию задачи, и генерацией этих вариантов.
ЗАДАЧИ ДЛЯ ПОВТОРЕНИЯ
1. Сколькими способами можно раскрасить вершины куба в три цвета (например, красный, синий и зеленый)? Напечатать все возможные способы.
2.
Сколькими различными способами можно надеть на нить семь бусин двух
цветов — синего и белого? Напечатать все возможные варианты. ![]()
З. Сколько различных ожерелий из семи бусин можно составить из бусин двух цветов — синего и белого? (Под ожерельем понимается замкнутая нить с нанизанными бусинами.) Напечатать все возможные варианты.
4. Сколько различных ожерелий можно составить из двух белых, двух синих и двух красных бусин? Напечатать все возможные варианты.
5. Сколькими различными способами можно грани куба раскрасить в четыре цвета? Напечатать все возможные варианты.
6. Грани куба можно раскрасить: а) все в белый цвет; б) все в черный цвет; в) часть в белый, а остальные в черный. Сколько имеется различных способов раскраски? Напечатать все возможные варианты.
7.
Напечатать все четырехзначные десятичные числа, у которых все цифры
разные. Обобщить на ![]() числа.
числа.
8.
Дама собирается пригласить семерых своих друзей на несколько званых
обедов. Ее стол, однако, невелик, да и обед «в узком кругу» несомненно гораздо
приятнее. Поэтому она решает приглашать каждый раз лишь троих гостей. Кроме того,
ей хочется, чтобы каждые двое ее друзей непременно встретились за ее столом,
причем она предпочла бы, чтобы они встретились лишь однажды. Как хозяйке
распределить приглашения по ![]() дням?
дням?
9. Написать алгоритм выплаты заданной суммы денег всеми возможными способами. В наличии имеются купюры достоинством l, 2, 5, 10, 20 и 100 дол.ларов. Количество купюр каждого вида не ограничено.
10. Написать программу, которая из букв А, В и С построит слово длины М, в котором два любых стоящих рядом подслова различны. Например:
слово АВСАВА составлено правильно; слово САВАВС составлено неправильно, так как сочетания букв АВ стоят рядом.
11. Существуют числа, обладающие свойствами: число делится на все свои цифры; число, полученное из данного записью цифр в обратном порядке, тоже делится на все свои цифры. Примером такого числа является 216. Составить программу для печати всех трехзначных чисел, обладающих этими свойствами. Числа с одинаковыми первой и последней цифрой не печатать.
12. Составить алгоритм получения словаря племени тумба-юмба, если известно, что:
алфавит языка этого племени содержит 4 буквы — а,
![]()
слова на языке этого племени не содержат двух и более одинаковых букв подряд.
13. Клетчатое поле п Х п охраняется т воинами царя Артаксеркса, занимающими различные клетки этого поля. Царь хочет расположить воинов так, чтобы обеспечить максимальную суммарную защищенность границы своего владения, т. е. 4 (п— 1) клеток непосредственно примыкающих к полю. Каждый воин охраняет те приграничные клетки, которые он «видит» по горизонтали, вертикали и диагоналям. При этом, защищенность клетки пропорциональна количеству воинов, ее охраняющих. Помогите Артаксерксу найти хотя бы одно положение воинов по его желанию.
14. У четырех кубиков грани окрашены в четыре разных цвета: красный, синий, зеленый и оранжевый. Развертки этих четырех кубиков выглядят следующим образом:
|
|
|
|
О |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
з |
|
о |
|
||||||||||||
|
з |
к |
к о |
|
з |
к с |
о |
||||||||||
|
|
с |
|
|
О |
|
|||||||||||
Написать программу, которая составляла бы из этих четырех кубиков прямоугольную призму, каждая боковая грань которой раскрашена во все четыре цвета без повторений.
ЗАДАЧИ ПОВЫШЕННОЙ СЛОЖНОСТИ
1. Дана строка S и набор А слов А 1, . .. , Ак. Разбить строку S на слова набора всеми возможными способами. П р и м е р: S=ABBC
![]() А В ВС
А В ВС
![]() А ВВС
А ВВС
![]() АВ ВС
АВ ВС
2. В написанном выражении ((((l?2)?3)?4)?5)?6 вместо каждого знака «?» вставить знак одной из 4 арифметических операций (+, / ) так, чтобы результат вычислений равнялся 35 (при делении дробная часть в частном отбрасывается). Найти все решения.
З. Составить программу, которая печатает Все различные представления числа N в виде всевозможных сумм натуральных чисел. Представления числа, отличающиеся только порядком слагаемых, считаются одинаковыми.
4.
Написать программу, отвечающую на вопрос, можно ли из N данных
прямоугольников Щ размеров (щ, bi), ![]() 1, ..., N, сложить один большой
прямоугольник П размера (а, Ь). Нижний левый угол большого прямоугольника имеет
координату (0; 0), стороны параллельны осям координат; маленькие прямоугольники
можно поворачивать, но так, чтобы их стороны после поворота оставались
параллельны осям координат. При составлении П прямоугольники Пе. могут быть
использованы не все.
1, ..., N, сложить один большой
прямоугольник П размера (а, Ь). Нижний левый угол большого прямоугольника имеет
координату (0; 0), стороны параллельны осям координат; маленькие прямоугольники
можно поворачивать, но так, чтобы их стороны после поворота оставались
параллельны осям координат. При составлении П прямоугольники Пе. могут быть
использованы не все.
Прямоугольники ПЕ не перекрываются.
Ограничения: N<8; а, Ь, щ, Т — целые числа.
Ответ выдать в виде «да» — «нет», и в случае «да» необходимо выдать для каждого прямоугольника По образующего П, координату его левого нижнего и правого верхнего углов и его номер i.
5. Игровой автомат состоит из нескольких изогнутых трубок, по форме похожих на перевернутую букву У. Сверху у трубы находится входное отверстие, а два выходных отверстия снизу. Труба может находиться в одном из двух возможных состояний. Состояние — это состояние, в котором закрыт левый выход, Состояние О — закрыт правый выход.
Шарики кладутся внутрь один за другим через входное
отверстие. В Состоянии I (рис. 33, а) шарик покидает трубу через
незаблокированный правый выход, при этом Состояние автоматически изменяется на
Состояние 0 ((рис. 33, б), правый вход заблокирован, левый — ![]() В Состоянии
0 все происходит наоборот.
В Состоянии
0 все происходит наоборот.
![]() а Вход
а Вход 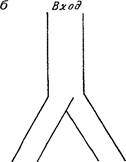
пеЬый 6D[X0d праЉ[й бьигВ лева; 6blXDd правш- 5ыхоВ
Рис. 33
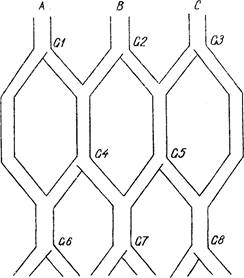
РИС. 34
Пусть игральный автомат состоит из 8 У-образных трубок, их взаимное расположение показано на рисунке 34. Вы можете забрасывать шарики через Вход А, Вход В или Вход С. Пусть, например, первый шарик опускается через Вход А. Он покидает трубу Gl через левый выход, изменяя ее состояние с О на 1, поступает в и покидает автомат через левый выход (16 (изменяя Состояние (16 с 0 на 1). Эту процедуру запишем следующим образом:
Затем забросим шарик через Вход А (он находится в Состоянии 1). Шарик покидает Gl через правый выход, изменяя Состояние 1 в Состояние О, попадает в G4, покидает через правый выход, изменяя Состояние I в Состояние 0, попадает в G7, покидает автомат через левый выход (изменяя из Состояния 0 в Состояние 1). Все вышеизложенные действия мы запишем в виде:
Если мы опустим третий шарик через Вход В, четвертый — через Вход С, то все действия запишутся следующим образом:
ААВС
Необходимо:
1)
Ввести с клавиатуры последовательность из 8 двоичных цифр (бит),
показываЮIЦИХ соответственно начальное Состояние —![]()
|
Бит |
7 |
6 |
5 |
4 |
|
2 |
|
0 |
|
Вход |
|
|
|
|
|
|
|
CJl |
Например, последовательность 11001010 означает, что G8, (17, и G2 находятся в Состоянии 1 (левый вход заблокирован), тогда как 06, (75, (13 и Gl находятся в Состоянии 0 (правый вход заблокирован).
2)
![]()
![]()
![]()
![]()
![]() Ввести с клавиатуры вторую последовательность из 8 бит,
показывающих конечные Состояния СЛ — G'8.
Ввести с клавиатуры вторую последовательность из 8 бит,
показывающих конечные Состояния СЛ — G'8.
З) Напечатать последовательность ходов А, В или С, указывающую, каким образом можно получить конечную позицию, забрасывая шарики через Входы А, В и С.
6. Пусть слово — это последовательность от 1 до
8 заглавных букв латинского алфавита.
Задается множество слов А =--{а [1], а
[2],![]()
![]() 10. Из слов множества А составляется
текст
10. Из слов множества А составляется
текст ![]() последовательность слов, записанных друг
за другом без пробелов. Слова могут встречаться в тексте произвольное число
раз.
последовательность слов, записанных друг
за другом без пробелов. Слова могут встречаться в тексте произвольное число
раз.
Дешифровка текста — это разбивка текста на слова множества А. В дешифрованном тексте слова разделяются пробелами.
![]() Необходимо:
Необходимо:
1) Определить, существует ли для заданного множества А такой текст, который дешифруется не единственным образом (сам текст приводить не надо).
![]() Пример ы:
Пример ы:![]()
![]()
Любой текст дешифруется однозначно.
![]()
Существует текст, который дешифруется двумя способами:
Текст ![]() Дешифровка
Дешифровка
2) Если такой текст существует, то исключить из множества А
минимальное число слов так, чтобы после этого любой текст, составленный из слов
полученного множества А, дешифровался однозначно. Напечатать эти исключенные
слова. Если такой набор не единственный, то напечатать все наборы. ![]()
П р и м е ч а н и е. Порядок выполнения пунктов строго фиксирован.
![]() ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
ЗАДАЧИ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ ![]()
![]() 1. Во время поездки на поезде девочка
заменила в названии поезда каждую букву ее номером в русском алфавите и
получила запись из единиц и двоек «211221—21221». Определить, откуда и куда
идет поезд.
1. Во время поездки на поезде девочка
заменила в названии поезда каждую букву ее номером в русском алфавите и
получила запись из единиц и двоек «211221—21221». Определить, откуда и куда
идет поезд.
2. Данные N косточек домино по правилам игры выкладываются в прямую цепочку, начиная с косточки, выбранной произвольно, в оба конца до тех пор, пока это возможно. Построить алгоритм, позволяющий определить такой вариант выкладывания заданных косточек, при котором к моменту, когда цепочка не может быть продолжена, «на руках» останется максимальное число очков.
З. В клетках таблицы расставлены числа. Расставить в этих клетках К ферзей так, чтобы они друг друга не
били и чтобы сумма чисел, ими закрываемых, была максимальной.
4. Вводится строка не более чем из 6 цифр и некоторое целое число R. Расставить знаки арифметических операций + , / (деление есть деление нацело, т. е. 11/3=3) и открывающие и закрывающие круглые скобки так, чтобы получить в результате вычисления число R. Лишние круглые скобки ошибкой не являются. Например: Строка 502597, R = 120:
![]() —120.
—120.
5. Перечислить все расстановки скобок в произведении п сомножителей. Порядок сомножителей не меняется, скобки полностью определяют порядок действий. (Например, для есть 5 расстановок:
((ab) c)d, (а (bc))d, (ab) (cd), a ((bc) d), а (Ь (cd)).)
6. ![]()
![]()
![]()
7. Составить
программу, которая печатает все различные представления числа N в виде
всевозможных произведений К натуральных чисел (N, К — вводятся, ![]() Если К —0,
то выдать все возможные произведения. Представления числа, отличающиеся только
порядком сомножителей, считаются одинаковыми.
Если К —0,
то выдать все возможные произведения. Представления числа, отличающиеся только
порядком сомножителей, считаются одинаковыми.
8. В некоей детской книге страницы разделены на три части, причем каждую часть можно перелистывать отдельно. На каждой странице трехсложные имена зверей расположены так, что каждый слог находится на одной части страницы; например, слоги стоят так: E-lefant, kro-ko-dil, kan-gu-ruh. После перелистывания одной части страницы возможны совмещения: kro-ko-fant, Капle-dil.
Написать программу:
а) с помощью которой трехсложные имена
зверей ![]() можно будет добавлять в книгу;
можно будет добавлять в книгу;
б) которая находит и протоколирует, как можно перелистывать книгу, чтобы найти путь от одного данного имени животного к другому;
в) которая, решив пункт б), находит несколько способов перелистывания.
9. Если кто-то захочет развести в аквариуме экзотических рыб, то он не сможет обойтись без совета эксперта. При покупке следует иметь в виду, что не каждый вид рыб уживается с другим видом и, конечно, рыбы несовместимых видов не должны жить вместе в аквариуме и бороться или даже поедать друг друга.
Необходимо написать программу, которая запрашивает:
а) сумму, которой распоряжаются при покупке рыб;
б) имеющиеся виды рыб с ценами за штуку;
в) виды рыб, не переносящие друг друга.
Покупателю должен быть выписан чек на максимально возможную сумму, с перечислением видов рыб, которые могут уживаться друг с другом.
10. Дырокол пробивает на длинной полосе бумаги по два одинаковых отверстия за одно нажатие его рычага и после нескольких нажатий получается следующее состояние бумаги.
|
о |
о |
о |
|
О |
оо |
оо |
о |
о |
л п л пл п лл пп л п
Буквы Л и П под лентой обозначают соответственно левое и правое отверстия дырокола.
По известным координатам отверстий на полосе определить возможную ширину между отверстиями дырокола.
11. В билете пассажира
оказалось пробито отверстий ![]() больше, чем штырей в компостере. Пассажир
утверждал, что пользовался только одним компостером, но случайно нажал на него
несколько раз. Контролеру требуется определить, могло ли быть получено заданное
расположение отверстий одним и тем же компостером, если билет можно пробивать с
обеих сторон неограниченное число раз и произвольно перемещать и поворачивать
относительно компостера. Пробитые отверстия не выходят за пределы билета. В
билете было пробито N 10) отверстий.
больше, чем штырей в компостере. Пассажир
утверждал, что пользовался только одним компостером, но случайно нажал на него
несколько раз. Контролеру требуется определить, могло ли быть получено заданное
расположение отверстий одним и тем же компостером, если билет можно пробивать с
обеих сторон неограниченное число раз и произвольно перемещать и поворачивать
относительно компостера. Пробитые отверстия не выходят за пределы билета. В
билете было пробито N 10) отверстий.
1) Для компостера с двумя штырями (S=2) составить программу, которая:
а) определяет, можно ли получить заданным компостером требуемое расположение отверстий в билете (если это возможно, то изображает вид билета после каждого нажатия компостера, в противном случае выводит соответствующее сообщение); б) определяет количество К различных компостеров, каждым из которых можно пробить заданную конфигурацию;
г) находит минимальное число нажатий, требуемое для пробивки заданной конфигурации отверстий, для каждого компостера из п. б).
2) Решить задачу 1) для компостеров с числом штырей S (S>2).
П р и меч а н и я.
1. Все исходные данные — натуральные числа.
2. Компостеры, дающие при однократном нажатии совпадающие конфигурации отверстий, считаются одинаковыми.
З. Относительное расположение отверстий в билете и
штырей в компостере вводится либо с клавиатуры, либо из файла с именем ![]() COMP.DAT. Структура вводимой
информации:
COMP.DAT. Структура вводимой
информации:
где x[i], у [i] — координаты отверстий в билете, и о [i] —
координа![]() ты штырей в компостере.
ты штырей в компостере.
4. Нажатие компостера моделировать клавишей «Пробел».
5. При выводе конфигурации на экран изображать координатную сетку. При этом программа должна осуществлять подходящее масштабирование.
![]() 12. Одним из стандартных методов
кодирования ин
12. Одним из стандартных методов
кодирования ин![]() формации когда-то был следующий: текст
(длины l) записывался по строкам слева направо сверху вниз в прямоугольнике
размера
формации когда-то был следующий: текст
(длины l) записывался по строкам слева направо сверху вниз в прямоугольнике
размера ![]() l), дополняясь, по необходимости,
пробелами; после этого текст из прямоугольника выписывался по столбцам и
получалось
l), дополняясь, по необходимости,
пробелами; после этого текст из прямоугольника выписывался по столбцам и
получалось ![]() шифрованное сообщение.
шифрованное сообщение.
Например, исходный текст «lt is а nice weather today» (т— 5, П=б):
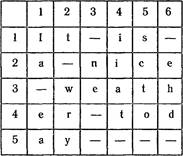
Шифрованный текст: «Та eat wry пе iiat scto ehd».
Дается шифрованный текст длины s, состоящий из букв и
пробелов, и известно, что в исходном тексте есть, по крайней мере, одно из слов
набора ао, . . . , ак, 10. Под словом в тексте понимается последовательность
символов, не содержащая пробелов, и окруженная пробелами, за исключением
случаев, когда слово стоит в начале либо в конце текста (тогда ему может не
пред![]() шествовать или за ним может не
следовать)“ один или несколько пробелов. Дешифровать текст.
шествовать или за ним может не
следовать)“ один или несколько пробелов. Дешифровать текст.
13. «Царевна>>. В одной из клеток поля размера п Х п 1) Кощей Бессмертный спрятал Марью Царевну, создав еще неизвестное число т (l п2 ) ее двойников в различных свободных клетках. И царевна, и ее двойники одинаково надежно укрыты и невидимы.
Отправившийся на поиски царевны Иванушка-дурачок попросил у благоволящей к нему щуки датчик биосигналов. Известно, что и Марья Царевна и ее двойники испускают незатухающие направленные биолучи, распространяющиеся параллельно сторонам и диагоналям поля.
Иванушка-дурачок также знает, что интенсивность биолуча Марьи Царевны в т раз выше интенсивности биолучей двойников. Иванушка может установить свой датчик в любую клетку поля и получить величину суммарной интенсивности биолучей, приходящих в клетку.
Помогите Иванушке определить местонахождение настоящей царевны.
14. К Штирлицу попала закодированная записка Бормана:
![]() 15, 16, 16, 16, 16, 4, 5, 8, 31, 25, 20, 2, 19, 18.
15, 16, 16, 16, 16, 4, 5, 8, 31, 25, 20, 2, 19, 18.
Штирлиц знал, что Борман пишет по-русски, используя обычную нумерацию букв в русском алфавите от 1 до 33. Пробел между словами он обозначает номером 0. Также он знал, что Борман кодирует свои сообщения, добавляя к номеру каждой буквы число х=па+Ь, где п — порядковый номер этой буквы в сообщении, а и Ь — константы, известные только Борману. Если результат оказывается больше 33, то из него вычитается 34. Кроме того, Борман ни в одном сообщении не обходится без местоимения «Я». Расшифруйте записку.
15. На доске размера 3Х3 произвольным образом расставлены фишки, занумерованные от I до 7. За один ход можно передвинуть фишку на свободное соседнее поле по горизонтали или по вертикали. Написать программу, приводящую фишки в конечную позицию:
|
1 |
2 |
|
|
4 |
5 |
6 |
|
7 |
|
|
![]() 16. На оси Ох были заданы точек с
целочисленными координатами. Некоторые точки могут иметь одинаковые координаты.
Были измерены и записаны всевозможные расстояния между этими точками.
Расстояние между двумя точками мы храним только один раз, расстояние от точки
до нее самой (равное 0) не хранится, поэтому расстояний всего N (N— 1)/2.
16. На оси Ох были заданы точек с
целочисленными координатами. Некоторые точки могут иметь одинаковые координаты.
Были измерены и записаны всевозможные расстояния между этими точками.
Расстояние между двумя точками мы храним только один раз, расстояние от точки
до нее самой (равное 0) не хранится, поэтому расстояний всего N (N— 1)/2.
Необходимо по введенной последовательности из N (N— 1 )/2 расстояний найти одно из возможных расположений точек на прямой или указать, что такого не существует.
17. Даны 4 слова. Длина каждого слова не более 12 символов. Написать программу, проверяющую, можно ли из данных слов составить кроссворд при условии, что каждое слово пересекается с двумя другими и располагается сверху вниз или слева направо. Сетка не обязательно симметрична. Результат вывести на экран в виде кроссворда.
![]()
![]() В вод:
вводятся 4 слова, по одному в строке.
В вод:
вводятся 4 слова, по одному в строке.
Вывод: на экран выводится один из вариантов кроссворда или
слово ”Нельзя' ![]() Пример:
Пример:
|
Ввод: |
Вывод: |
|
АЛЬФА АСТРА ФАКИР АВАРИЯ |
АЛЬФА |
АВАРИЯ
18. Напечатать все последовательности из К положительных целых чисел, у которых Ј-й член не превосходит г.
19. Построить
все отображения множества {l, ![]()
![]() п} (предполагается,
что К С), такие, что ни один элемент не переходит сам в себя. Порождение
очередного элемента должно требовать порядка К действий.
п} (предполагается,
что К С), такие, что ни один элемент не переходит сам в себя. Порождение
очередного элемента должно требовать порядка К действий.
20. Напечатать все перестановки чисел 1, 2, . , п так, чтобы каждая следующая получалась из предыдущей перестановкой (транспозицией) двух соседних чисел. Например, при допустим такой порядок:
![]()
(между переставляемыми числами вставлены точки).
21. Элементами последовательности длины 2п могут быть числа или —1. Сумма всех элементов последовательности равна нулю. Перечислить все такие последовательности, у которых сумма любого начального отрезка положительна (т. е. число минус единиц в нем не превосходит числа единиц).
22. На окружности задано 2п точек, пронумерованных от I до 2п. Перечислить все способы проведения п непересекающихся хорд с вершинами в этих точках.
23. Перечислить все последовательности из п нулей, единиц и двоек, в которых никакая группа цифр не повторяется два раза подряд (нет куска вида ХХ).
24. Есть N карточек. На каждой из них черными чернилами написан ее уникальный номер — число от I до М. Также на каждой карточке красными чернилами написано еще одно целое число, лежащее в промежутке от до N (некоторыми одинаковыми «красными» числами могут помечаться несколько карточек).
Например, N=5; 5 карточек помечены следующим образом:
|
«Черное» число |
|
2 |
З |
4 |
5 |
|
<<Красное» число |
з |
з |
2 |
4 |
|
Необходимо выбрать из данных N карточек максимальное число карточек таким образом, чтобы множества «красных» и «черных» чисел на них совпадали.
Для рассмотренного примера это будут карточки с «черными» номерами 2, З, 4 (множество красных номеров, как и требуется в задаче, то же —- {2, З, 4}).
10 Информатика, 8—9 кл )
<”Черный” номер 1, ”красный”— > ”красное” число_1
< ”Черный“ номер N, ”красный”— ”красное —чис-
J10—N вывод:
![]() выбранном множестве элементов
количество—элементов S
выбранном множестве элементов
количество—элементов S
<”Черные” номера выбранных карточек> al, . , aS 25. «Тетрамино». Дано поле размера 6Х6 клеток. Клетки пронумерованы от 1 до 36 слева направо и сверху вниз (как при письме).
![]() Ровно четыре клетки из них закрашены. Написать программу,
которая для введенных номеров закрашенных клеток выясняет, образуют ли они
какую-либо фигуру тетрамино (эти фигуры могут быть повернуты):
Ровно четыре клетки из них закрашены. Написать программу,
которая для введенных номеров закрашенных клеток выясняет, образуют ли они
какую-либо фигуру тетрамино (эти фигуры могут быть повернуты):
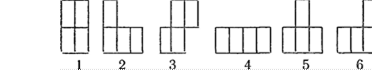
Если введенный номер меньше I или больше 36, или какой-то номер введен повторно, то вывести сообщение ”Ошибка”.
Если закрашенные клетки образуют фигуру тетрамино, вывести номер этого тетрамино, в противном случае выдать сообщение: ”Не тетрамино”.
Пусть закрашены N клеток. Число N и номера этих клеток вводятся. Определить, можно ли разбить закращенную область на фигуры тетрамино. Фигуры не могут пересекаться, и объединение этих фигур полностью совпадает с закрашенной областью.
разбить”. В случае, если разбивка возможна, выд,ать какую-нибудь разбивку в виде:
Номер фигуры. Номера образующих ее клеток.
Номер фигуры. Номера образующих ее клеток.
26. Имеется N (N<7) дисков одинаковой толщины С радиусами rt, rn. Эти диски упаковываются в коробку таким образом, что каждый из них стоит ребром на дне коробки и все диски находятся в одной плоскости.
Найти минимальную длину коробки, в которую все они могут быть упакованы, и указать порядок одной из возможных упаковок.
Вход:
![]() 1-я строка
1-я строка ![]() <2-я
строка
<2-я
строка ![]() Выход:
Выход:
Минимальная длина: число Возможный порядок: порядок П р имер:
Минимальная длина: 9.65685
Возможный порядок: 1 3 2
УКАЗАНИЯ К РЕШЕНИЮ ЗАДАЧ ПОВЫШЕННОЙ СЛОЖНОСТИ
1. Эта задача реализуется следующим рекурсивным алгоритмом поиска с возвращением (все слова набора А упорядочены по номерам).
а) Если строка пустая, то одна из возможных дешифровок найдена, иначе — при разборе текста мы проверяем АЕ (при изменении i от до п) на вхождение в начало дешифруемой в данный момент строки.
б) Если какое-то Аг входит в строку как
префикс, то запоминаем номер i этого слова, затем выделяем слово из строки, а с
остатком текста производим ![]() операцию разбора по пункту а).
операцию разбора по пункту а).
![]()
Если ни одно из Д не входит в качестве приставки в дешифруемую сейчас строку, то осуществляем возврат на пункт а), предварительно добавляя в начало строки последнее удаленное оттуда слово, и пытаемся выделить из текста слово с большим номеров в А. Если возврат осуществить невозможно (так как мы находимся в начале исходной строки), то алгоритм заканчивает свою работу, Все возможные дешифровки найдены.
2.
![]() Всего может быть 4 арифметических операции (Н- ,
Всего может быть 4 арифметических операции (Н- , ![]() /).
Занумеруем их от 0 до З. Вместо каждого из пяти знаков «?» может стоять один из
знаков операции. Заведем массив А из 5 целых чисел, в i-M элементе массива
будет храниться код соответствующей i-MY знаку «?» операции, т. е. число от 0
до З. Начальная конфигурация — все элементы массива нулевые, конечная
/).
Занумеруем их от 0 до З. Вместо каждого из пяти знаков «?» может стоять один из
знаков операции. Заведем массив А из 5 целых чисел, в i-M элементе массива
будет храниться код соответствующей i-MY знаку «?» операции, т. е. число от 0
до З. Начальная конфигурация — все элементы массива нулевые, конечная ![]() все
они равны З. Генерация очередной конфигурации знаков равносильна прибавлению
единицы в четверичной системе счисления, в которой разрешается пользоваться
только цифрами от О до З. Такая генерация описана в алгоритме (5.3).
все
они равны З. Генерация очередной конфигурации знаков равносильна прибавлению
единицы в четверичной системе счисления, в которой разрешается пользоваться
только цифрами от О до З. Такая генерация описана в алгоритме (5.3).
З. Предложим простой способ построения всех разбиений числа на слагаемые. Разбиения будут строиться в порядке, обратном лексикографическому. Очевидно, что первым разбиением в таком порядке будет разбиение, содержащее одно слагаемое, равное N, а последним — разбиение из N слагаемых, равных 1.
Как выглядит разбиение, следующее непосредственно за разбиением
![]()
Будем искать разбиение, которое имеет самое большое число начальных слагаемых, равных начальным слагаемым данного разбиения (обозначим эти слагаемые щ, . . . , а, _1) и оставшиеся слагаемые которого определяются разбиением, непосредственно следующим за разбиением
![]()
Легко видеть, что эти условия однозначно определяют значение t :
t=max l}.
Таким образом, задача свелась к нахождению разбиения, непосредственно следующего за разбиением
![]()
где а— 1, а количество
единиц равно К— l. Таким разбиением является разбиение ![]() mod р),
mod р),
4. Каждый ГИ можно положить либо горизонтально, либо вертикально. Будем заполнять П от нижнего левого угла.
На каждом шаге:
1) искать в уже заполненной фигуре ”нишу” с минимальными координатами левого нижнего угла;
2) для каждого из еще не использованных П, повторять брать очередной f1i и пытаться вставить в
'нишу” ![]() если удалось, и мы не
вышли за пределы П, то пометить 11i как использованный и на шаг
если удалось, и мы не
вышли за пределы П, то пометить 11i как использованный и на шаг ![]() scratch:
scratch:
пометить IIi как неиспользованный конец то конец для если использовали все Щ, то печать результата. Стоп если не использован ни один П„ то решения нет иначе возврат на scratch.
![]() 5. Во всех узлах (трубках) схемы мы должны получить
состояние G'i. Первоначально установим (П, G2 и G3 в Gf, G'2 и (Ц, вбрасывая,
по необходимости, шарики через входы А, В и С соответственно. Для того чтобы
Gl, G2 и G3 оставались в состоянии ф, и 66, необходимо, чтобы через каждый из
входов забрасывалось лишь четное число шариков.
5. Во всех узлах (трубках) схемы мы должны получить
состояние G'i. Первоначально установим (П, G2 и G3 в Gf, G'2 и (Ц, вбрасывая,
по необходимости, шарики через входы А, В и С соответственно. Для того чтобы
Gl, G2 и G3 оставались в состоянии ф, и 66, необходимо, чтобы через каждый из
входов забрасывалось лишь четное число шариков.
Если проследить за шариками, заброшенными в игровой автомат, то мы можем заметить, что результат хода, например, АВС аналогичен результату хода ВСА, т. е. от порядка забрасывания результат ке зависит.
Рассмотрим узлы, состояние которых может меняться при забрасыва-
Аналогично для забрасывания шариков через В мы получаем серию из не более чем 25 =32 пар шариков, на протяжении которой будут установлены все возможные состояния G4, 65, 66, G7, (78, а для входа С серия, как и для А, будет иметь длину не более 8 пар.
Перебирая все возможные комбинации А2х, Ви, C2z забрасывания
шариков (тут 142х обозначает серию из 2х забрасываний шариков через вход А,
О<х, у<8, ![]()
![]() получаем либо
комбинацию — решение задачи, либо определяем отсутствие решения.
получаем либо
комбинацию — решение задачи, либо определяем отсутствие решения.
6. Один из возможных алгоритмов решения задачи такой: ![]()
![]()
![]()
Рис. 36
1) Предположим, что существует текст, дешифровка которого неоднозначна, следовательно, существует и текст минимальной длины, для которого возможны по меньшей мере две разбивки ь [1] ь [21... ь [1] с [21. ..с [т]
на слова множества А. Представляя текст в виде отрезка DE, эти разбивки мы можем изобразить, как на рисунке 36.
Из того, что текст минимальной длины, следует, что концы слов в разных разбивках не могут лежать на одной вертикали (кроме конца текста). Так как Ь [1]+
![]() [1], то одно из кодовых слов (например, Ь
[Ц) должно входить в другое в качестве префикса и представляться в виде
[1], то одно из кодовых слов (например, Ь
[Ц) должно входить в другое в качестве префикса и представляться в виде ![]() [1]
р где р [1] — оставшаяся часть слова (суффикс). Далее, либо р [1] входит в Ь
[2] (Ь [2]
[1]
р где р [1] — оставшаяся часть слова (суффикс). Далее, либо р [1] входит в Ь
[2] (Ь [2] ![]()
![]() либо Ь [2] входит в p
[l] (р [2] р [Ц) в качестве префикса. Определяем новый суффикс р
либо Ь [2] входит в p
[l] (р [2] р [Ц) в качестве префикса. Определяем новый суффикс р ![]() Продолжая
выделять префиксы и суффиксы, получасм, что на каком-то шаге р [ј] совпадает с
одним из кодовых слов.
Продолжая
выделять префиксы и суффиксы, получасм, что на каком-то шаге р [ј] совпадает с
одним из кодовых слов.
Эти рассуждения являются основой следующего алгоритма.
На нулевом шаге возьмем все пары (а [i]; а. i+j таких кодовых слов, что одно из них есть префикс другого, и найдем все суффиксы р [0, К].
На ј-м шаге для всех пар (р [ј— 1, К]; а где одно из слов является префиксом другого, опять находим все суффиксы, и те из них, которые не появлялись на предыдущих шагах алгоритма, обозначим р [ј, К],
![]()
Эти шаги повторяем либо до тех пор, пока какой-либо суффикс не совпадает с одним из кодовых слов (и тогда существует неоднозначно декодируемый текст), либо пока на очередном шаге не появится ни одного нового суффикса (и тогда для любого текста существует единственная дешифровка).
Так как количество кодовых слов ограничено, то и суффиксов также конечное число, и на каком-то шаге алгоритм обязательно остановится.
Этот алгоритм в первоначальном варианте принадлежит А. Сардинасу и Дж. Паттерсону (Кибернетический сборник. Вып. З. С. 93—102).
2) Если существует текст, который при использовании А дешифруется неоднозначно, то начинаем выбрасывать из А слова и их комбинации, пытаясь получить множество [4' с максимальным числом слов такое, что все тексты, составленные из слов дешифруются однозначно.
Сначала из А удаляем i-e слово, 2 п, и делаем проверку по пункту 1). Если удалением одного слова из А мы не получаем искомого множества А“, то тогда генерируем все сочетания по п— 2 слова из множества А и для каждого полученного множества делаем проверку по пункту 1) и т. д.
Воспользуемся алгоритмом (5.2) генерации сочетаний по i слов из множества А.
З) Этот пункт реализуется следующим рекурсивным алгоритмом поиска с возвращением (все слова массива А упорядочены по номерам):
а) если строка пустая, то одна из возможных дешифровок найдена, иначе при разборе текста мы проверяем a [i] (при изменении i от до п) на вхождение в начало дешифруемой в данный момент строки.
б) если какое-то а [i] входит в строку как префикс, то запоминаем номер i этого слова, затем выделяем слово из строки, а с остатком текста производим операцию разбора по пункту а).
Если ни одно из а [i] не входит в качестве префикса в дешифруемую сейчас строку, то осуществляем возврат на пункт а), предварительно добавляя в начало строки последнее удаленное оттуда слово, и пытаемся выделить из текста слово с большим номером в А. Если возврат осуществить невозможно (так как мы находимся в начале исходной строки), то алгоритм заканчивает свою работу. Все возможные дешифровки найдены.
З адач а 1. Докажите следующую теорему (Марков А. А.):
Для однозначности декодировки текста достаточно выполнения одного из двух следующих условий:
1)
не существует ни одной пары кодовых слов (а [i], а ![]() такой, что
одно из этих слов есть префикс другого.
такой, что
одно из этих слов есть префикс другого.
2)
не существует ни одной пары кодовых слов (а [i], а ![]() такой, что
одно из них есть суффикс другого.
такой, что
одно из них есть суффикс другого.
З а да ч а 2. Приведите пример такого множества кодовых слов, что для него не выполняется ни условие 1, ни условие 2 из задачи 1, а декодировка любого текста, составленного при помощи этих слов,— однозначная.
![]()
![]()

if then
![]()
ZI :=(x3-x1 )-(y3-y1 )*(x2-x1 );
![]() Z2:=(x4-x1
)*(y2-y1 )-(y4-y1 ) ;
Z2:=(x4-x1
)*(y2-y1 )-(y4-y1 ) ;

 for begin
for begin ![]() mod n+l; k:=j mod n+l;
mod n+l; k:=j mod n+l;
if i=l then
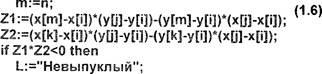
end;
![]()
p:=(a+b+c)/2
![]()
![]()
![]()
for k:=l to n+l do
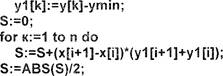
![]()
![]()
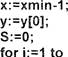 for to n do begin
for to n do begin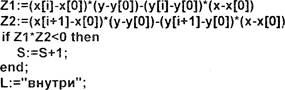
if S mod 2 = 0 then
![]()
283

for i:=l to N do if then
![]()
while (i<=n) and (A[il<>X)

![]()
end
![]()
max:=A[1]; for i:=2 to N do if A[i]>max then
![]()
for i:=2 to N do if ![]() then begin
then begin
 for begin
for begin![]()
for j:=i+l to N do if Aül>max then begin
![]()
end;
![]()
end;
![]()
for i:=l to N —1 do for j:=l to N — i do if Aül<ALj+1] then begin
![]()
end;
![]()
![]()
for j:=l to R
do ![]() then begin
then begin
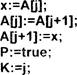
end; end;
![]()
![]() while
(L<=R) and (P=fa!se) do begin div 2; then
while
(L<=R) and (P=fa!se) do begin div 2; then
else if then
![]()
end;
![]()
![]() while (L<R) do
begin div 2; then
while (L<R) do
begin div 2; then
end; if then p:=true else p:=faise
![]()
while (l<r) do begin m:=(l+r) div
2; if ![]() then l:=m+l
then l:=m+l
r:=m; end;
![]()
for j:=i downto k+l do
![]()
![]()
begin if ![]() then begin
then begin
C[Ci]•. = A[Ai];
![]()
end (2.14)
![]()
if (Ai>N) and (Ci<>N+M) then for i: = Bi to M do begin ccci]: = BF];
![]() = Ci + l; end; if (Bi>M) and (Ci<>N+M) then for i: = Ai to N do
begin
= Ci + l; end; if (Bi>M) and (Ci<>N+M) then for i: = Ai to N do
begin
![]()
end; end; { while }

p:='He AenhTC"';
![]()
![]()
end;
![]()
for i:=2 to trunc(sqrt(a))+l do if (a mod i=O) and (i<a) then
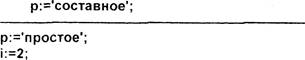
(3.4) if (a mod i=O) and (i<a) then
![]()
![]()
n:=(n+l) div 2;
while j<=n do begin
![]()
while i<=n do begin
![]()
end;
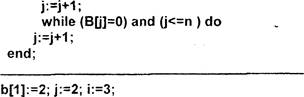
while i<=n do begin
if b[k]>d then begin
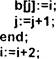
end;
![]()
while a>l do if a mod then begin
![]()
![]()
![]()
while a<>b do if a>b then a:=a-b
b:=b-a; nod:=a;
![]()
while (a<>O) and (b<>O) do if a>b then a:=a mod b
b:=b mod a; if then nod:=b e!se nod:=a;
![]() mod 10;
mod 10;
N:- N div 10; end;
![]()
while L>=l do begin ![]() div 10; end;
div 10; end;
white N>=l do begin ![]() mod 10;
mod 10; ![]() div 10; end;
div 10; end;
![]()
![]()
a:=0; r:=l ; for i:=l to N do begin (3.13) a:=a+B[i]*r; r:=r*10; end;
![]()
(3.14) ![]() mod p;
mod p;
![]()
![]() r:=l; to N begin
r:=l; to N begin ![]() mod m;
mod m;
end;
![]()
if N>M then else
![]()
for i:=l to K do
for to K do begin
![]()
end; end; if then
![]()
for i:=l to N do
for to N do begin
![]()
![]()
![]() end; end;
while
end; end;
while
291
K
for i:=l to M do for j:=l to N do
for ![]() begin
begin ![]() div 10;
div 10;
end; ![]() while
while

![]()
![]()
![]()
for i:=2 to N do begin c:=b+a; a:=b; b:=c;
![]()
N
![]()
for j:=2 to 6 do
![]() ,j-ll, ACI ,j]); for i:=2 to 5 do
,j-ll, ACI ,j]); for i:=2 to 5 do
![]()
![]()
end;
![]()
for i:=3 to 10 do

![]()
![]()
end
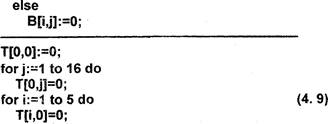
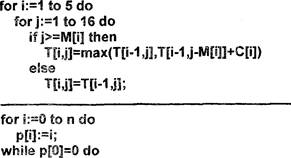
begin for ![]() writedn; while pü-ll>pü]
do
writedn; while pü-ll>pü]
do
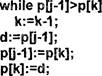 do
dofor i:=j to n
do for ![]() end;
end;
![]()
repeat ![]() for writeln;
for writeln;
while (j>0) and ![]() do
do
if j<>O then begin
![]()
![]()
end; until j=O;
 while begin
while begin
![]() whiåe and (A[m] = O) do begin
whiåe and (A[m] = O) do begin
![]()
![]()
write\n; end;
![]()
while do begin
(5.4) end;
for i:=O to n-l do
![]()
write\n•, end;
![]()
summa:=O; for
i:=l to n do ![]() otvet:='HeT peweHHR' if summa mod 2 1 then writetn('HeT peweHHR') else
begin summa:=summa div 2; for to n-l do for to n do if then begin
otvet:='HeT peweHHR' if summa mod 2 1 then writetn('HeT peweHHR') else
begin summa:=summa div 2; for to n-l do for to n do if then begin
![]()
end;
 then begin otvet:='HeT peueHhR'•,
then begin otvet:='HeT peueHhR'•,
end:
while ![]() and (otvet='HeT pet.ueH"9') do
begin while (i<=n) and (otvet='HeT peweHh9') do begin {while}
and (otvet='HeT pet.ueH"9') do
begin while (i<=n) and (otvet='HeT peweHh9') do begin {while}
![]()
if s=summa then begin write!n; writeln('pe1ueHue:'),• for j:=l to stackCOl do
![]()
296
halt; end else begin if s<summa then begin
![]()
i:=i+l; end; end; {while)
![]()
end; { stack[ll } writeln; writeIn('HeT peweHh9. ');
end; {else}
СОДЕРЖАНИЕ
От авторов![]()
Глава 1. Уравнение прямой
|
S 1. Прямые
и отрезки на плоскости 1.1. Формы записи уравнения прямой |
4 |
|
1.2. Положение точек относительно прямой |
7 |
|
1.3. Взаимное расположение двух отрезков |
9 |
|
1.4. Точка пересечения отрезков |
[2 |
|
S 2. Расстояние на плоскости 2.1. Расстояние между точками. Расстояние от точки до
прямой |
[3 |
|
2.2.
Расстояние между точкой и отрезком S З. Многоугольники 3.1.
Виды многоугольников 3.2. Выпуклость многоугольников |
15 |
|
S 4. Площади фигур 4.1. Площадь треугольника |
19 |
|
4.2. Площадь прямоугольника 4.3. Площадь трапеции |
20 |
|
4.4. Площадь плоского многоугольника |
21 |
|
S 5. Взаимное расположение фигур на плоскости 5.1. Взаимное расположение многоугольника
и точки |
23 |
|
5.2. Взаимное расположение многоугольников |
26 |
|
Задачи для повторения |
27 |
|
Задачи повышенной сложности |
29 |
|
Задачи для самостоятельного решения |
38 |
|
Указания
к решению задач повышенной сложности Глава 2. Поиск и сортировки |
40 |
|
|
66 |
|
|
70 |
|
|
71 |
|
|
72 |
|
3.2. Сортировка обменом |
74 |
|
|
78 |
298
|
S Другие виды сортировок 5.1. Сортировка вставками |
81 |
|
5.2. Сортировка слияниями |
83 |
|
Задачи для повторения |
85 |
|
Задачи повышенной сложности |
90 |
|
Задачи для самостоятельного решения |
94 |
|
Указания
к решению задач повышенной сложности Глава З. Алгоритмы целочисленной арифметики |
98 |
|
S 1. Поиск делителей числа. Простые числа |
116 |
|
S 2. Разложение числа на простые множители S З. Поиск наибольшего общего делителя (НОД) и наименьшего |
122 |
|
общего кратного (НОК) 3.1. поиск нод |
125 |
|
3.2. поиск нок |
128 |
|
S 4. Представление чисел. Выделение цифр числа 4.1. Преобразование числа из обычного представления в таб- |
129 |
|
личное 4.2. Преобразование табличного представления числа в обыч- |
130 |
|
ное |
132 |
|
S 5. Перевод чисел из одной системы счисления в
другую |
134 |
|
S 6. Делимость чисел |
136 |
|
S 7. Действия с многозначными (большими) числами 7.1. Сложение многозначных чисел |
139 |
|
7.2. Вычитание многозначных чисел |
141 |
|
7.3*. Произведение многозначных чисел |
142 |
|
Задачи для повторения |
143 |
|
Задачи повышенной сложности |
149 |
Задачи для самостоятельного решения![]() 154
154
Указания к решению задач повышенной сложности![]() 159
159
Глава 4. Рекуррентные соотношения и динамическое программирование
1. Понятие задачи и подзадачи 176
2.
Сведение задачи к
подзадачам 178 ![]() З. Понятие рекуррентного соотношения 179 S 4. Правильные рекуррентные
соотношения 182
З. Понятие рекуррентного соотношения 179 S 4. Правильные рекуррентные
соотношения 182
![]() 5. Способ организации таблиц 184
5. Способ организации таблиц 184
5.1. Организация одномерных таблиц 185
5.2. Организация двумерных таблиц 186
6. Способ вычисления элементов таблицы 188
6.1.
Вычисление
элементов одномерной таблицы![]()
6.2. Вычисление элементов двумерной таблицы 190
![]() 6.3. Вычисление элементов двумерной
таблицы с дополнительными ограничениями 192
6.3. Вычисление элементов двумерной
таблицы с дополнительными ограничениями 192
Задачи для повторения![]() 195
195
Задачи повышенной сложности![]() 198
198
Задачи для самостоятельного решения![]() 202
202
Указания к решению задач повышенной СЈIОЖНОСТИ![]() 208
208
Глава 5, Задачи комбинаторики
S 1. Соединения![]() 236
236
1.1. Перестановки![]()
1.2. Сочетания![]() 240 l.3*. Размещения
240 l.3*. Размещения![]() 242
242
S 2* Соединения с повторениями![]() 244
244
2.1. Размещения с повторениями![]()
2.2. Перестановки с повторениями![]() 246
246
2.3. Сочетания с повторениями![]() 247
247
S 3*. Г[одмножества![]() 249
249
S 4.
Реализация перебора вариантов. Сокращение перебора ![]() 251
251
Задачи для повторения![]() 260
260
Задачи повышенной сложности![]() 262
262
Задачи для самостоятельного решения![]() 266
266
Указания к решению задач повышенной сложности![]() 275
275
Приложения![]() 282
282
Учебное издание
Котов Владимир Михайлович
Волков Игорь Анатольевич Лапо Анжелика Ивановна
ИНФОРМАТИКА
Методы алгоритмизации
Учебное пособие для 8—9 классов общеобразовательной школы с углубленным изучением информатики с русским языком обучения
Редактор Н. Г. Левчук. Художественный редактор Л. В. Павленко. Технический редактор С. И. Лицкевш. Корректоры З. Н. Гришели, С А. Янович.
Сдано в набор 29.08.2000. Подписано в печать ![]() Бумага
Бумага ![]() офсетная N2 1. Формат 84Х 108 1 /32.
Гарнитура литературная. Высокая печать с ФПФ. Усл.-печ. л. 15,96. Усл. кр.-отт.
16,38. Уч.-изд. л. 12,12.
офсетная N2 1. Формат 84Х 108 1 /32.
Гарнитура литературная. Высокая печать с ФПФ. Усл.-печ. л. 15,96. Усл. кр.-отт.
16,38. Уч.-изд. л. 12,12.
Тираж 28 100 экз. Заказ 1566.
Налоговая льгота — Общегосударственный классификатор Республики Беларусь ОКРБ-98, ч. 1; 22.11.20.100.
Издательское республиканское унитарное предприятие «Народная асвета» Государственного комитета Республики Беларусь по печати. Лицензия ЛВ 4 от 08.09.2000. 220600, Минск, проспект Машерова, l l .
Республиканское унитарное предприятие «Полиграфический комбинат имени Я. Коласа». 220600, Минск, Красная, 23
Котов В. Мо и др.
К95 Информатика. Методы алгоритмизации:
Учеб. пособие для 8—9-х кл. общеобразоват. шк. с углубл. изучением информатики
с рус. языком обучения / В. М. Котов, И. А. Волков, А. И. Лапо.![]()
Мн.: Нар. асвета, 2000.—300 с.: ил.
ISBN 985-12-0259-2
удк 1002.6+681.31 (075.3=82) ББК 32.81я721.6
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.