
Г. М. Нурмухамедов, Л. Ф. Соловьева

Санкт-Петербург
«БХВ-Петербург»
2012
УДК 681.3.06(075.3)
ББК 32.973.я729
Н90
Нурмухамедов, Г. М.
Н90 Информатика.Теоретические основы. Учебное пособие для подготовки к ЕГЭ / Г. М. Нурмухамедов, Л. Ф. Соловьева. — СПб.: БХВ-Петербург, 2012. — 208 с.: ил. + CD-ROM —
(ИиИКТ)
ISBN 978-5-9775-0871-1
Книга предназначена для углубленной подготовки учащихся 11 клас сов и выпускников общеобразовательных школ по тео ре тической информатике и включает следующие разделы: информатика и инфор мация, устройство ЭВМ, двоичная арифметика, бинарная логи ка, информационные системы, информационные модели, основы тео рии алгоритмов, программный способ записи алгоритмов. Предста в ленные материалы также могут быть полезны студентам сред них специальных учебных заведений и младших курсов профиль ных вузов. Книга сопровождается авторским компакт-ди ском, со держа щим электронную версию книги с элементами интер активного обучения.
Для образовательных учреждений
УДК 681.3.06(075.3)
ББК 32.973.я729 Группа подготовки издания:
Главный редактор Екатерина Кондукова
Зав. редакцией Елена Васильева
Редактор Анна Кузьмина
Компьютерная верстка Натальи Караваевой
Корректор Наталия Першакова
Дизайн серии Инны Тачиной
Цветовое решение обложки и коллаж Людмилы Соловьевой
Подписано в печать 30.07.12.
Формат 60х901/16. Печать офсетная. Усл. печ. л. 13.
Тираж 1000 экз. Заказ №
«БХВ-Петербург», 191036, Санкт-Петербург, Гончарная ул., 20.
Первая Академическая типография «Наука»
199034, Санкт-Петербург, 9 линия, 12/28
|
ISBN 978-5-9775-0871-1 |
© Нурмухамедов Г. М., гл. 1–6, 2012 |
|
|
|
© Соловьева Л. Ф., гл. 7, 8, 2012 |
|
|
|
© Оформление, издательство «БХВ-Петербург», 2012 |
|
|
Содержание 3
|
|||
Оглавление
Введение ................................................................................................................5
Глава 1. Информатика и информация ............................................................9
Что такое информатика .........................................................................................9
Структура информатики .....................................................................................12
Теоретическая информатика ..............................................................................12
Искусственный интеллект ..................................................................................14
Программирование .............................................................................................15
Прикладная информатика ..................................................................................16
Вычислительная техника ....................................................................................18
Кибернетика.........................................................................................................18
Информация и ее свойства .................................................................................19
Понятие «информация» ......................................................................................19
Свойства информации ........................................................................................23
Вопросы и задания ..............................................................................................27
Глава 2. Устройство ЭВМ ................................................................................29
Современный персональный компьютер ..........................................................29
Структура ЭВМ ...................................................................................................29
Принципы работы ЭВМ .....................................................................................30
Эволюция ЭВМ ...................................................................................................34
Появление первых ЭВМ .....................................................................................34
Первое поколение ЭВМ (1955–1960) ................................................................34
Второе поколение ЭВМ (1960–1965) ................................................................35
Третье поколение ЭВМ (1965–1970) .................................................................35
Четвертое поколение ЭВМ (1970–1990) ...........................................................36
Пятое поколение ЭВМ (с 1990 г. и по настоящее время) ................................36
Сравнительные характеристики ЭВМ различных поколений ........................37
Перспективы дальнейшего развития ЭВМ .......................................................37
Программное обеспечение ЭВМ .......................................................................39 Элементная база ЭВМ ........................................................................................43
Понятие об элементной базе ЭВМ. Типы транзисторов.
Полупроводниковые интегральные схемы .......................................................43
Технология изготовления полупроводниковых интегральных схем ..............45
Структура и принцип работы базовых электронных элементов ....................47
Инвертор ........................................................................................................47
Вентиль ..........................................................................................................48
Триггер ...........................................................................................................50
Регистры .........................................................................................................51
Вопросы и задания ..............................................................................................52
Ответы и решения ...............................................................................................54
Глава 3. Двоичная арифметика ......................................................................57
Системы счисления .............................................................................................57
Преобразование чисел в различных системах счисления ...............................61
Представление информации в ЭВМ ..................................................................64
Арифметические операции с двоичными числами .........................................67
Сложение и вычитание .......................................................................................67
4 Оглавление
![]()
Умножение и деление .........................................................................................68 Вопросы и задания ..............................................................................................70 Ответы и решения ...............................................................................................72
Глава 4. Бинарная логика ...............................................................................79 Алгебра логики ....................................................................................................79 Законы алгебры логики ......................................................................................83 Однотактные и многотактные автоматы ...........................................................85 Вопросы и задания ..............................................................................................97 Ответы и решения ...............................................................................................99
Глава 5. Информационные системы ...........................................................105 Понятие «система»............................................................................................105 Понятие «информационная система» .............................................................111 Классификация информационных систем ......................................................114 Классификация по используемой технической базе ......................................114 Классификация по степени автоматизации ....................................................115 Классификация по структурированности задач .............................................117 Классификация по функциональному назначению .......................................118
Вопросы и задания ............................................................................................119
Глава 6. Информационные модели ..............................................................121 Понятие «модель» .............................................................................................121 Понятие «информационная модель» ...............................................................124 Классификация информационных моделей ...................................................126 Вопросы и задания ............................................................................................132
Глава 7. Основы теории алгоритмов ...........................................................133
Понятие алгоритма. Исполнители алгоритмов. Система команд
исполнителя .......................................................................................................133 Свойства алгоритмов и способы их записи ....................................................135 Базовые алгоритмические структуры .............................................................139 Построение алгоритмов и представление их в виде блок-схем ...................145
Исполнители алгоритмов .................................................................................148 Вопросы и задания ............................................................................................153 Ответы и решения .............................................................................................158
Глава 8. Программный способ записи алгоритмов ..................................163 Языки и среды программирования ..................................................................163 Основные элементы языка Object Pascal ........................................................165 Операторы присваивания и ввода/вывода ......................................................172
Условные операторы.Простые и составные условия.Логические
операции в условиях .........................................................................................174
Операторы цикла с параметром, предусловием и постусловием .................178
Сортировка и поиск данных в массиве ...........................................................185
Подпрограммы. Процедуры и функции. Принципы структурного
программирования ............................................................................................189
Символьные и строковые переменные. Операторы, процедуры
и функции обработки строковых переменных ...............................................194 Вопросы и задания ............................................................................................197 Ответы и решения .............................................................................................203
Заключение .......................................................................................................207 Приложение. Описание компакт-диска .........................................................208
|
Двоичная арифметика 5
|
Учебное пособие предназначено тем, кто решил поступать в технический вуз и будет сдавать ЕГЭ по информатике. Пособие можно использовать также в качестве основы для элективного курса, расширяющего знания учащихся в области теоретической информатики.
Книга и соответствующий курс включает 8 разделов: «Информатика и информация», «Устройство ЭВМ», «Двоичная арифметика», «Бинарная логика», «Информационные системы», «Информационные модели», «Основы теории алгоритмов», «Программный способ записи алгоритмов» и рассчитан на 70 часов учебного времени. Материал изложен компактно, в виде конспекта лекций, по- этому им удобно будет пользоваться и на уроках, и при подготовке к экзамену по информатике.
Книга сопровождается авторским компакт-диском, содержащим электронную версию изучаемого материала.
Учебно-тематический план курса
«Информатика. Теоретические основы»
|
№ п/п |
Тема |
Количество часов |
||
|
тео- рия |
прак- тика |
все- го |
||
|
1 |
Информатика и информация |
2,5 |
1,5 |
4 |
|
1.1 |
Что такое информатика |
0,5 |
|
0,5 |
|
1.2 |
Структура информатики |
1 |
0,5 |
1,5 |
|
1.3 |
Информация и ее свойства |
1 |
1 |
2 |
|
2 |
Устройство ЭВМ |
5,5 |
3,5 |
9 |
|
2.1 |
Современный персональный компьютер |
0,5 |
|
0,5 |
6 Введение
![]()
Продолжение
|
№ п/п |
Тема |
Количество часов |
||
|
тео- рия |
прак- тика |
все- го |
||
|
2.3 |
Программное обеспечение ЭВМ |
1,5 |
0,5 |
2 |
|
2.4 |
Эволюция ЭВМ |
0,5 |
0,5 |
1 |
|
2.5 |
Элементная база ЭВМ |
1 |
1 |
2 |
|
2.6 |
Технология изготовления полупроводниковых интегральных схем |
0,5 |
0,5 |
1 |
|
2.7 |
Структура и принципы работы базовых электронных элементов |
1 |
1 |
2 |
|
3 |
Двоичная арифметика |
3 |
3 |
6 |
|
3.1 |
Системы счисления |
0,5 |
0,5 |
1 |
|
3.2 |
Представление информации в ЭВМ |
1 |
1 |
2 |
|
3.3 |
Преобразование чисел в различных системах счисления |
1,5 |
1,5 |
3 |
|
4 |
Бинарная логика |
6 |
5 |
11 |
|
4.1 |
Алгебра логики |
1 |
1 |
2 |
|
4.2 |
Законы алгебры логики |
2 |
2 |
4 |
|
4.3 |
Однотактные и многотактные автоматы |
3 |
2 |
5 |
|
5 |
Информационные системы |
4 |
|
4 |
|
5.1 |
Понятие «система» |
2 |
|
2 |
|
5.2 |
Понятие «информационная система» |
1 |
|
1 |
|
5.3 |
Классификация информационных систем |
1 |
|
1 |
|
6 |
Информационные модели |
4 |
|
4 |
|
6.1 |
Понятие «модель» |
1 |
|
1 |
|
6.2 |
Понятие «информационная модель» |
1 |
|
1 |
|
6.3 |
Классификация информационных моделей |
2 |
|
2 |
Введение 7
![]()
Окончание
|
№ п/п |
Тема |
Количество часов |
||
|
тео- рия |
прак- тика |
все- го |
||
|
7 |
Основы теории алгоритмов |
6 |
6 |
12 |
|
7.1 |
Понятие алгоритма. Исполнители алгоритмов. Система команд исполнителя |
0,5 |
0,5 |
1 |
|
7.2 |
Свойства алгоритмов и способы их записи |
1 |
0,5 |
1,5 |
|
7.3 |
Базовые алгоритмические структуры |
1,5 |
1,5 |
3 |
|
7.4 |
Построение алгоритмов и представление их в виде блок-схем |
1,5 |
1,5 |
3 |
|
7.5 |
Исполнители алгоритмов |
1,5 |
2 |
3,5 |
|
8 |
Программный способ записи алгоритмов |
8 |
10 |
18 |
|
8.1 |
Языки и среды программирования |
0,5 |
|
0,5 |
|
8.2 |
Основные элементы языка Object Pascal |
1 |
1 |
2 |
|
8.3 |
Операторы присваивания и ввода/ вывода |
0,5 |
0,5 |
1 |
|
8.4 |
Условные операторы. Простые и составные условия, логические операции в условиях |
1,5 |
1,5 |
3 |
|
8.5 |
Операторы цикла с параметром, предусловием и постусловием |
1,5 |
2 |
3,5 |
|
8.6 |
Сортировка и поиск данных в массиве |
1 |
2 |
3 |
|
8.7 |
Подпрограммы. Процедуры и функции. Принципы структурного программирования |
1 |
1,5 |
2,5 |
|
8.8 |
Символьные и строковые переменные. Операторы, процедуры и функции обработки строковых переменных |
1 |
1,5 |
2,5 |
|
|
Резерв |
2 |
|
2 |
|
|
ИТОГО |
41 |
29 |
70 |
Глава 1
ИнформатИка И ИнформацИя
|
Информатика и информация 9
|
Слово «информатика» (informatique) возникло в 1960-х гг. во Франции как объединение двух терминов — «информация» (infor mation) и «автоматика» (automatique) и первоначально означало «информационная автоматика» или «автоматизированная переработка информации». Этот термин вошел в обиход и в других странах, в том числе в СССР, а затем и в России. Однако в англо- язычных странах используется другой термин — computer science (вычислительная наука).
Информатика в современном ее представлении родилась с появлением ЭВМ, развивается вместе с развитием компьютерной техники и не может без нее существовать. За прошедшие полвека содержание понятия «информатика» трансформировалось так, что теперь информатика представляет собой единство разнообразных отраслей науки, техники и производства, связанных с переработкой информации во всех сферах человеческой деятельности.
Из множества определений информатики приведем несколько, лучше всего отражающих суть этого понятия.
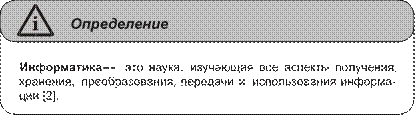
 Информатика — комплексная научная и
инженерная дисциплина, изучающая все аспекты разработки, проектирования,
создания, оценки, функционирования, основанных на ЭВМ систем переработки
информации, их применения и воздействия на различные области социальной
практики. (Принято на сессии годичного собрания Академии наук СССР в 1983
г.)
Информатика — комплексная научная и
инженерная дисциплина, изучающая все аспекты разработки, проектирования,
создания, оценки, функционирования, основанных на ЭВМ систем переработки
информации, их применения и воздействия на различные области социальной
практики. (Принято на сессии годичного собрания Академии наук СССР в 1983
г.)
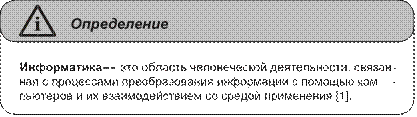
Во всех приведенных определениях понятия «информатика» используется другое проблемное понятие — «информация», т. е. происходит объяснение одного термина через другой, что само по себе не корректно. Истолкование понятия «информация» мы рассмотрим в разд. «Информация и ее свойства» далее в этой главе, а здесь приведем еще одно определение информатики.
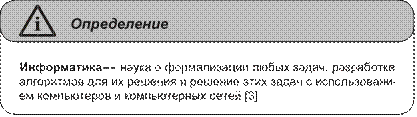
В настоящее время информатика используется в самых разных областях науки, техники и производства, связанных с переработкой информации с помощью компьютеров и телекоммуникационных средств связи (компьютерных сетей), а также во всех сферах человеческой деятельности.
Предметом нашего рассмотрения является информатика как современная синтетическая наука, объединившая в себе множество различных аспектов классических наук (естественных и гуманитарных), связанных тем или иным образом с информационными объектами. Информация, как основной и единственный объект изучения в информатике, по своей сути очень многогранна и выступает в различных проявлениях. С учетом этого можно выделить в информатике ряд основных направлений, к рассмотрению которых мы перейдем в следующем разделе.
1. Информатика: Учебник / Под ред. Н. В. Макаровой. — М.: Финансы и статистика, 1999.
2. Информатика: Энциклопедический словарь для начинающих / Сост. Д. А. Поспелов. — М.: Педагогика-Пресс, 1994.
3. Фридланд А. Я. Информатика: процессы, системы, ресурсы. — М.: БИНОМ. Лаборатория знаний, 2003.
На рис. 1.1 представлена структура информатики как научной и прикладной дисциплины, в которой выделены шесть основных научно-технических направлений:
1. Теоретическая информатика.
2. Искусственный интеллект.
3. Программирование.
4. Прикладная информатика.
5. Вычислительная техника.
6. Кибернетика.
Эти разделы информатики перечислены не в порядке их важности или преемственности, а лишь с учетом удобства их расположения на рисунке. Краткая характеристика каждому направлению будет дана в указанном выше порядке.
Теоретический раздел любой науки базируется на математиче ских методах исследования. Это относится и к информатике. Она использует методы математики для построения и изучения моделей обработки, передачи и использования информации, создает тот теоретический фундамент, на котором строится все здание информатики.
По своей природе информация дискретна и представляется обычно в символьно-цифровом виде в текстах и точечном виде на рисунках. С учетом этого в информатике широко используется математическая логика как раздел дискретной математики. (Соответствующий материал, посвященный математической логике, представлен в главе 4 «Бинарная логика».) Следующее направление теоретической информатики — вычислительная математика, которая разрабатывает методы решения задач на компьютерах с использованием алгоритмов и программ.
Подраздел «Теория информации» (а также «Теория кодирования и передачи информации») изучает информацию в виде абстрактного объекта, лишенного конкретного содержания. Здесь исследуются
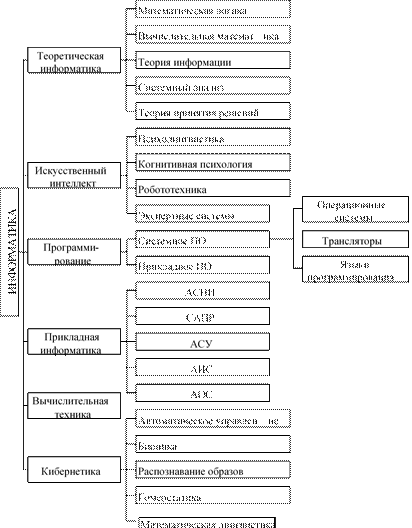
Рис. 1.1. Структура дисциплины «Информатика»
общие свойства информации и законы, управляющие ее рождением, развитием и уничтожением. Также изучаются те формы, в которые может отобразиться содержание любой конкретной элементарной единицы информации.
Системный анализ — еще одно направление теоретической информатики. В нем изучается структура реальных объектов, явлений, процессов и определяются способы их формализованного описания через информационные модели. Имитационное модели рование — один из важнейших методов компьютерного моделиро вания, в котором воспроизводятся процессы и явления, протекающие в реальных объектах.
Наконец, теория принятия решений изучает общие схемы выбора нужного решения из множества альтернативных возможностей. Такой выбор часто происходит в условиях конфликта или противоборства. Модели такого типа изучаются в теории игр.
Это направление информатики — одно из самых молодых, оно возникло в середине 1970-х гг. Однако именно искусственный интеллект определяет стратегические направления развития информатики.
Искусственный интеллект тесно связан с теоретической ин форматикой, из которой он заимствовал многие модели и методы (например, использование логических средств для преобразования знаний). Столь же прочны связи этого направления с кибернетикой. Математическая и прикладная лингвистика, нейрокибернетика и гомеостатика также теснейшим образом связаны с развитием искусственного интеллекта. И конечно, работы в этой области немыслимы без развития систем программирования.
Основная цель работ в области искусственного интеллекта — стремление проникнуть в тайны творческой деятельности людей, их способности к овладению знаниями, навыками и умениями. Для этого необходимо раскрыть те глубинные механизмы, с помощью которых человек способен обучиться практически любому виду деятельности. И если суть этих механизмов будет разгадана, то есть надежда реализовать их подобие в искусственных системах, сделав их по-настоящему интеллектуальными. Такая цель исследований в области искусственного интеллекта тесно связывает их с достижениями психологии — науки, одной из задач которой является изучение интеллекта человека и в которой сегодня активно развивается особое направление — когнитивная психология. Исследования в нем направлены на раскрытие закономерностей и механизмов, связанных с процессами познавательной деятельности человека и интересующих специалистов в области искусственного интеллекта.
Другое направление психологии — психолингвистика — также интересует специалистов в области искусственного интеллекта. Ее результаты касаются моделирования общения не только с помощью естественного языка, но и с использованием иных средств — жестов, мимики, интонации и т. п.
Кроме теоретических исследований активно развиваются и прикладные аспекты искусственного интеллекта. Например, робототехника занимается созданием технических систем, которые способны действовать в реальной среде и частично или полностью заменить человека в некоторых сферах его интеллектуальной и производственной деятельности. Такие системы получили название роботов.
Экспертные системы — еще одно прикладное направление искусственного интеллекта. В отличие от других интеллектуальных систем, экспертная система имеет три главные особенности:
1. Она адаптирована для любого пользователя.
2. Она позволяет получать не только новые знания, но и профессиональные умения и навыки, связанные с данными знаниями, т. е. обеспечивает ответ не только на вопрос «что знать?», но и «как знать?».
3. Она передает не только знания, но и пояснения и разъяснения,
т. е. обладает обучающей функцией.
Программирование как научное направление возникло с появлением вычислительных машин и только программное обеспечение определяет эффективность использования ЭВМ. В настоящее время это достаточно продвинутое направление информатики. В этой области работает значительное число специалистов, которые подразделяются на системных и прикладных программистов.
Системные программисты являются, как правило, специалистами очень высокого уровня и разрабатывают системное программное обеспечение, которое включает в себя операционные системы, языки программирования и трансляторы.
r Операционные системы обеспечивают функционирование вычислительной техники и предоставляют пользователю комфортные условия взаимодействия с компьютером.
r Языки программирования создаются для разработки прикладного программного обеспечения. В основном это языки высокого уровня, мнемоника и семантика которых близка к естественному языку общения людей. Кроме них существуют также машинные языки, которые используются непосредственно в ЭВМ и состоят из последовательности машинных команд, реализованных в системе команд микропроцессора. Для преобразования программ, написанных на языке высокого уровня, в программы на машинном языке используются специальные программы — трансляторы, которые также создаются системными программистами.
Прикладное или проблемно-ориентированное программирование ориентировано на разработку пользовательских программ для решения тех или иных задач, возникающих в различных областях науки, техники и производства. Например, в сфере образования используются пакеты педагогических программных средств (ППС), в состав которых входят обучающие и контролирующие программные средства по определенной предметной области.
Достижения современной информатики широко используются в различных областях человеческой деятельности: в научных исследованиях (АСНИ — автоматизированные системы для научных исследований), в разработке новых промышленных изделий (САПР — системы автоматизированного проектирования), в информационных системах (АИС — автоматизированные информационные системы), в управлении (АСУ — автоматизированные системы управления), в обучении (АОС — автоматизированные обучающие системы) и др.
Здесь нам следует подробнее остановиться на характеристике информационной системы.
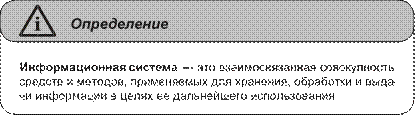
Структурно ИС состоит из технического, математического, программного, информационного и организационного обеспечения.
Техническое обеспечение — это комплекс технических средств (компьютеры, устройства сбора, накопления, обработки, передачи и вывода информации, устройства передачи данных, линии связи и др.) с соответствующей документацией на них и на технологические процессы обработки данных.
Математическое и программное обеспечение — это совокупность используемых математических методов, моделей, алгоритмов и программ.
Информационное обеспечение — это банк данных, блок расшифровки запросов и блок поиска.
Организационное обеспечение — это совокупность методов и средств, регламентирующих взаимодействие пользователей с техническими средствами системы.
Различные типы информационных систем перечислены ранее в этой главе.
Материал, посвященный вычислительной технике, будет рассмотрен в главе 2 «Устройство ЭВМ».
Термин «кибернетика» (от греч. κυβερνητης — кормчий) появился летом 1947 г. как результат обсуждения новой терминологии группой ученых во главе с Норбертом Винером, в течение целого ряда лет проводивших исследования в различных областях научных знаний (математической статистики, электросвязи, нейрофизиологии и др.), связанных с вопросами управления системами и объектами с помощью различного рода информационных сигналов. В 1948 г. Н. Винер опубликовал свою монографию под названием «Кибернетика, или управление и связь в животном и машине». Идея «общей теории управления» получила новое развитие с появлением компьютеров, способных решать самые разные задачи.
В 1940-е гг. наряду с идеей об универсальности схем управления в кибернетике развиваются и другие идеи: идея универсальной символики, идея логического исчисления, идея измерения информации через понятия вероятностной и статистической (термодинамической) теорий. Все эти и ряд других идей и направлений исследования так называемой «ничейной территории» между различными уже сложившимися науками впоследствии стали основой кибернетики, которую, в свою очередь, вобрала в себя информатика после создания и развития компьютерной техники.
Из всех современных направлений этой науки в настоящее время наиболее активно развивается техническая кибернетика. В ее состав входит теория автоматического управления, которая стала теоретическим фундаментом автоматики. Трудно переоценить важность исследований в этой области: без них невозможны были бы достижения в области приборостроения, станкостроения, атомной энергетики и других систем управления промышленными процессами и научными исследованиями.
Ведущее место в кибернетике занимает и распознавание образов. Основная задача этой дисциплины — поиск решающих правил, с помощью которых можно было бы классифицировать многочисленные явления реальности, соотносить их с некоторыми эталонными классами. Распознавание образов — это пограничная область между кибернетикой и искусственным интеллектом, поскольку поиск решающих правил чаще всего осуществляется путем обучения, а обучение — это, конечно же, интеллектуальная процедура.
Еще одно научное направление связывает кибернетику с биоло гией. Аналогии между функционированием живых и неживых систем уже многие столетия волнуют ученых. Насколько принципы работы живых систем могут быть использованы в искусственных объектах? Ответ на этот вопрос ищет бионика — пограничная наука между кибернетикой и биологией. В свою очередь, нейрокибер нетика пытается применить кибернетические модели в изучении структуры и действия нервных тканей.
Не так давно возникло (и еще находится в стадии формирования) еще одно научное направление кибернетики — гомеостатика, изучающее равновесные (устойчивые) состояния сложных взаимодействующих систем различного типа. Это могут быть социальные, автоматические системы и др.
Наконец, математическая лингвистика занимается исследованием особенностей естественных языков, а также моделей (формальных грамматик), позволяющих формализовать синтаксис и семантику таких языков. Это направление сегодня стало весьма актуальным в связи с развитием систем машинного перевода текстов с одних языков на другие.
Слово «информация» относится к основополагающим терминам информатики и в переводе с латинского означает «сообщение», «разъяснение». До появления компьютерной техники это слово использовалось редко — в основном в специальной и технической литературе.
Впервые термин «информация» приводится в книге Н. Винера «Кибернетика», однако лишь в узком смысле — в составе понятия «количество информации».
В настоящее время термин «информация» используется очень широко как в быту и на производстве, так и в науке, образовании, технической и популярной литературе. При этом смысл термина «информация» столь широк, что зачастую может вступать в противоречие с его контекстным содержанием.
Во многих публикациях делаются попытки дать «фундаментальное», «универсальное» толкование этого термина, отображающее его мировоззренческий и философский смысл наряду с такими философскими категориями как вещество и энергия. И если два последних понятия относятся к материальному миру, то, в противовес им, термин «информация» связывается с идеальными, нематериальными субстанциями.
В книге В. Шнейдерова «Занимательная информатика» [8] отмечено, что в настоящее время известно более четырехсот определений термина «информация». Для примера приведем некоторые из них.
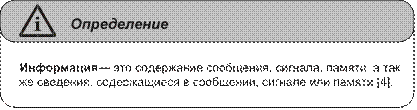
 Информация: первоначально — сведения,
передаваемые людьми, устным, письменным или другим способом (с помощью условных
сигналов, технических средств и т. д.); с середины в. — общенаучное понятие,
включающее обмен сведениями между людьми, человеком и автоматом, автоматом и
автоматом; обмен сигналами в животном и растительном мире; передачу признаков
от клетки к клетке, от организма к организму [1].
Информация: первоначально — сведения,
передаваемые людьми, устным, письменным или другим способом (с помощью условных
сигналов, технических средств и т. д.); с середины в. — общенаучное понятие,
включающее обмен сведениями между людьми, человеком и автоматом, автоматом и
автоматом; обмен сигналами в животном и растительном мире; передачу признаков
от клетки к клетке, от организма к организму [1].
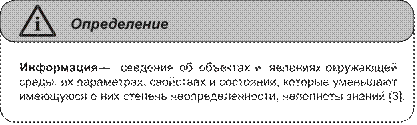
 Информация — содержание сообщения или
сигнала, сведения, рассматриваемые в процессе их передачи или восприятия; одна
из исходных общенаучных категорий, отражающая структуру материи и способы ее
познания, несводимая к другим, более простым понятиям [5].
Информация — содержание сообщения или
сигнала, сведения, рассматриваемые в процессе их передачи или восприятия; одна
из исходных общенаучных категорий, отражающая структуру материи и способы ее
познания, несводимая к другим, более простым понятиям [5].
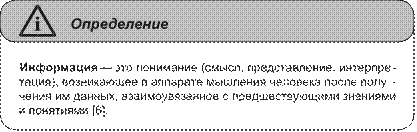
Приведенные выше определения информации как основного понятия информатики очень сильно отличаются друг от друга, хотя почти везде постулируется, что информация — это сведения. Согласно определению из книги [1] информацией могут обмениваться не только люди, но и автоматы, в то время как, согласно книге [6], информация возникает и существует лишь в мыслительном аппарате человека и нигде более. Как только эта информация отчуждается от человека, она превращается из сведений (смысла, знаний) в данные, и только если такие данные попадут к человеку, который знает закон (правила) интерпретации (придания смысла) этим данным, то у адресата данные вновь преобразуются в смысл. Причем смысл у источника и адресата в общем случае чаще всего не совпадает.
Подробно и обстоятельно понятие «информация» исследовано в книге [6]. Здесь же мы приведем лишь выводы из этого исследования.
1. Предлагается считать понятие «информация» субъективным понятием в том смысле, что понимание происходит только в аппарате мышления человека.
2. Человек не может получать информацию непосредственно. Он лишь может на основании каких-либо данных, представленных в виде сигналов, документов и т. д., сформировать у себя в аппарате мышления информацию о чем-либо.
3. Формирование информации в аппарате мышления человека происходит на основании как внешних данных, так и всего предшествующего опыта и знаний этого конкретного человека. Именно потому одно и то же сообщение, полученное разными людьми (или одним человеком, но в разное время), приводит к разным ответным реакциям.
4. Предложена модель процесса получения информации человеком:
внешние сигналы
↓ данные
↓
неформальный смысл, выраженный в ощущениях
↓
полуформальный смысл, выраженный в словах
↓
формальный смысл, выраженный в терминах логики
5. Предложена модель передачи информации от человека:
неформальный смысл
↓
полуформальный смысл, выраженный в тексте
↓
формальный смысл, выраженный в алгоритме
↓ данные
На основе сказанного выше становится ясно, что информатика как наука имеет дело скорее не с информацией, а с данными, т. е. слова «информация» и «данные» там выступают как синонимы. Более того, в официальных документах, различных популярных изданиях, на бытовом уровне и т. д. термин «информация» чаще всего тоже выступает в значении «данные». Мы также будем придерживаться этого правила, помня, что «информация» — это «данные для нас», а просто «данные» — это «данные в себе».
Одним из важнейших свойств информации является ее адекватность, т. е. степень соответствия образа, создаваемого с помощью полученной информации, реальному объекту (процессу, явлению). При этом различаются три формы адекватности информации: синтаксическая, семантическая и прагматическая [3].
1. Синтаксическая адекватность — отображает формально- структурные характеристики информации и не затрагивает ее смыслового содержания.
2. Семантическая (смысловая) адекватность — определяет степень соответствия информации об объекте самому этому объекту.
3. Прагматическая (потребительская) адекватность — отражает взаимоотношение информации и ее потребителя. Прагматический аспект связан с ценностью, полезностью использования информации потребителем для достижения им поставленной цели.
Меры информации. Информация (в смысле данных) всегда связана с некоторым материальным носителем: это может быть сигнал в любой материальной форме, числовой или символьный код на печатной основе и т. д. А поскольку любой материальный объект можно как-то измерить, то это относится и к ин- формации.
Что же можно измерить в ней?
Во-первых, можно количественно определить синтаксическую форму адекватности информации реальному объекту. Степень адекватности описываемому объекту зависит от количества слов (символов), затраченных на описание модели этого объекта. Поскольку каждый символ естественного языка можно закодировать одним байтом (8 бит), то нетрудно вычислить полный объем информации, связанный с описанием любого объекта, процесса, явления. Это так называемый алфавитный подход измерения количе ства информации.
Существует и другой количественный подход — кибернетиче ский, который учитывает ценность информации (ее прагматиче скую адекватность). Впервые он был предложен в работах К. Шеннона [7] и Н. Винера [2]. Изучая системы передачи информации, К. Шеннон пришел к выводу, что каждое элементарное сообщение на выходе системы уменьшает неопределенность исходного множества сообщений, причем собственно смысловой аспект сообщения в этом случае не имеет никакого значения. За единицу количества ин формации им было предложено принять «количество информации, передаваемое при одном выборе между двумя равновероятными альтернативами». Эта наименьшая единица информации называется битом. Информация в один бит уменьшает неопределенность информационной системы в два раза. Для вычисления среднего количества информации, связанного с положительным исходом некоторого события x из множества m событий, К. Шеннон предложил формулу:
Hx =−∑ pi log pi,
где pi — вероятность i-го события.
Эта формула (получившая название «формулы Шеннона») характеризует энтропию (меру неопределенности) системы. Изначально это понятие появилось в физике и характеризует степень неупорядоченности (неопределенности) микросостояния, в котором система (например, термодинамическая) может находиться в данный момент времени.
Значение Hx достигает максимума для равновероятных событий, т. е. при pi =1/ m формула Шеннона упрощается:
Hmax =−log pi = logm (формула Р. Хартли).
П р и м е р. Рассмотрим систему с 256 возможными состояниями, например расширенную кодовую таблицу символов. Тогда Hmax будет равно 8 битам. Другими словами, восьми битов достаточно, чтобы точно описать исход любого события, связанного с кодовой таблицей (например, выборку определенного символа из этой таблицы).
Содержательный (субъективный) подход. Содержание информации, кроме уже рассмотренного количественного (объективного) параметра, также имеет семантическую (смысловую) ха рактеристику, которая определяется способностью пользователя понимать поступившее сообщение. Эта способность зависит от тезауруса пользователя, т. е. от совокупности сведений и знаний, которыми располагает этот пользователь. Если тезаурус пользователя близок к нулю, то любая новая информация им не воспринимается (он ее просто не понимает), и в этом случае объем семантической компоненты информации для него равен нулю. Если поступившая информация не дает пользователю новых (полезных) знаний, то и в этом случае объем семантической компоненты информации также равен нулю. Максимальное же значение объема семантической компоненты информации пользователь получает, если поступившая информация понята им и несет ему новые сведения, знания. Таким образом, одно и то же сообщение может иметь важное смысловое содержание для компетентного пользователя и быть бессмысленным для пользователя некомпетентного.
Качество информации. Возможность и эффективность использования информации обуславливаются такими основными потребительскими показателями ее качества, как содержательность, репрезентативность, достаточность, доступность, актуаль ность, своевременность, точность, достоверность, устойчи вость. Многие из этих показателей очевидны и не требуют пояснений, поэтому мы остановимся лишь на некоторых из них.
Содержательность информации отражает семантическую емкость, равную отношению объема семантической компоненты информации, содержащейся в сообщении, к объему обрабатываемых данных.
Репрезентативность информации связана с правильностью ее отбора и формирования для адекватного отражения свойств объекта.
Достаточность (полнота) информации означает, что она содержит минимальный, но достаточный для принятия правильного решения набор сведений. Как неполная, так и избыточная информация снижает эффективность принимаемых пользователем решений.
1. Большой энциклопедический словарь. — М.: Большая Российская Энциклопедия, 1998.
2. Винер Н. Кибернетика, или управление и связь в животном и машине: Пер. с англ. — М.: Советское радио, 1958.
3. Информатика: Учебник / Под ред. Н. В. Макаровой. — М.: Финансы и статистика, 1999.
4. Информатика: Энциклопедический словарь для начинающих / Сост. Д. А. Поспелов. — М.: Педагогика-Пресс, 1994.
5. Математический энциклопедический словарь. — М.: Советская Энциклопедия, 1988.
6. Фридланд А. Я. Информатика: процессы, системы, ресурсы. —
М.: БИНОМ. Лаборатория знаний, 2003.
7. Шеннон К. Работы по теории информации и кибернетике: Пер. с англ. — М.: Иностранная литература, 1963.
8. Шнейдеров В. С. Занимательная информатика. — СПб.: Политехника, 1994.
1. В этой главе было приведено несколько различных определений понятия «информатика». Какое из них, на ваш взгляд, наиболее точно и полно отражает сущность этого понятия?
2. Используя древовидную структуру направлений развития современной информатики (см. рис. 1.1), укажите в ней разделы научной информатики. Обоснуйте свой выбор.
3. В чем состоит принципиальное различие между кибернетикой и информатикой?
4. В чем заключается различие между направлениями «Искусственный интеллект» и «Кибернетика»?
5. В этой главе приведено несколько разных определений и толкований понятия «информация». Какое из них вам представляется наиболее полно отражающим сущность этого понятия?
6. Охарактеризуйте основные свойства информации.
7. Какие подходы можно использовать для измерения количества информации?
8. С чем связано появление такой единицы измерения количества информации как бит?
Глава 2
Устройство ЭвМ
Вопрос для обсуждения
1. Каким стал бы компьютер, если бы вместо двоичной элементной базы для него была использована многозначная?
|
Устройство ЭВМ 29
|
2.  Как будет работать ЭВМ, построенная на оптической, химической, биологической и другой элементной базе?
Как будет работать ЭВМ, построенная на оптической, химической, биологической и другой элементной базе?
Структура ЭВМ (рис. 2.1) не зависит от ее технических характеристик, размеров и назначения — она едина для любой ЭВМ!
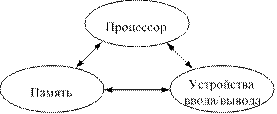
Рис. 2.1. Структура ЭВМ (общий вид)
Процессор является «сердцем» ЭВМ. Он исполняет программы и управляет работой остальных узлов машины.
Память подразделяется на внутреннюю (оперативную и постоянную) и долговременную.
Устройства ввода/вывода обеспечивают взаимодействие ЭВМ с человеком и с различными внешними информационными объектами.
Подробнее о назначении и характеристиках отдельных блоков и узлов ЭВМ мы поговорим в следующем разделе.
Принципы работы ЭВМ мы рассмотрим на примере персонального компьютера (ПЭВМ, ПК).
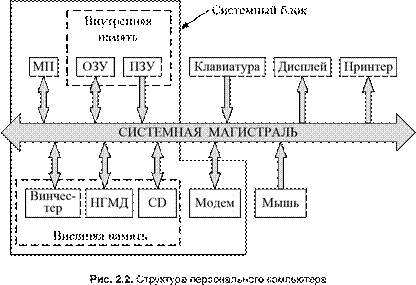
На рис. 2.2 представлена структура ПК. Его основу составляет системный блок, в котором размещены микропроцессор (МП), блоки оперативного запоминающего устройства (ОЗУ) и постоянного запоминающего устройства (ПЗУ), устройство долговременной памяти на жестком магнитном диске (винчестер), устройства для чтения/записи компакт-дисков (compact disk, CD) и дискет (накопители на гибких магнитных дисках, НГМД). В последние годы на смену дискетам пришли флеш-накопители (флешки), имеющие емкость от 4 до 256 Гбайт и подключаемые к компьютеру через разъем USB.
В системном блоке располагаются также вспомогательные блоки: сетевой, видеопамять, обработки звука, модем (модулятордемодулятор) и различные интерфейсные модули, обслуживающие внешние устройства ввода/вывода: клавиатуру, дисплей, мышь, принтер и др.
Все функциональные узлы ПК связаны между собой через системную магистраль, представляющую собой шину из более чем трех десятков упорядоченных микропроводников, сформированных на печатной плате.
Микропроцессор служит для обработки информации: он выбирает команды из внутренней памяти (ОЗУ или ПЗУ), расшифровывает, а затем исполняет их, производя требуемые арифметические и логические операции. Микропроцессор получает данные из устройства ввода и посылает результаты на устройства вывода. Он вырабатывает также сигналы управления и синхронизации для согласованной работы всех внутренних узлов ПК, контролирует работу системной магистрали и всех периферийных устройств.
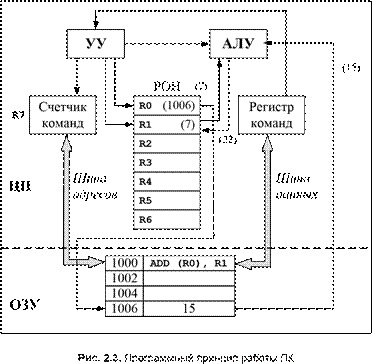
Упрощенная схема микропроцессора представлена на рис. 2.3[1] (выделена штриховой линией с надписью «ЦП»). В его состав входят:
r арифметико-логическое устройство (АЛУ), выполняющее арифметические и логические операции над двоичными числами;
r блок регистров общего назначения (РОН), используемых для временного хранения обрабатываемой информации (R0–R5), указателя стека (R6) и счетчика команд (R7);
r устройство управления (УУ), определяющее порядок работы всех узлов микропроцессора.
Одной из важнейших характеристик микропроцессора является его разрядность, определяемая количеством разрядов АЛУ и РОН. Современные микропроцессоры могут иметь разрядность 16, 32 и 64 бит, а также поддерживать до 200 и более различных внутренних команд.
Обработка информации осуществляется по программе, которая представляет собой последовательность команд, направляющих работу компьютера. Каждая такая команда состоит из кода операции и адреса. Код операции сообщает микропроцессору, что нужно сделать — какую выполнить операцию: сложить числа, сравнить их, переслать, очистить память и др. Адрес же указывает место, где находятся данные, подлежащие обработке.
Программы и данные размещаются в 8-битовых ячейках ОЗУ, адресация которых организована по байтам. Таким образом, 16-разрядный процессор за один такт извлекает информацию из двух таких ячеек, а 32-разрядный процессор — из четырех ячеек ОЗУ.
Команды микропроцессора бывают безадресными, одноадресными и двухадресными. Например, двухадресная команда сложения выглядит так:
|
ADD |
Адрес источника |
Адрес приемника |
Выполнение микропроцессором любой команды состоит из двух этапов: фазы выборки и фазы исполнения.
Фаза выборки начинается по сигналу начала цикла команды. При этом содержимое счетчика команд указывает на ее адрес в ОЗУ (например, 1000). Как только сигнал по шине адресов поступает в ОЗУ, содержимое счетчика команд увеличивается на 2 (для 16-разрядного процессора) и указывает на адрес следующей команды. Из ОЗУ по шине данных команда поступает в регистр команд микропроцессора. В данном случае это команда ADD(R0), R1.
Фаза исполнения начинается с расшифровки полученной команды. В нашем примере код операции ADD предписывает АЛУ сложить содержимое, которое находится в ОЗУ по адресу, содержащемуся в регистре источника, хранимому в регистре R0, с содержимым, размещенным в регистре R1, а результат поместить в регистр приемника R1.
На этом фаза исполнения данной команды завершается, а микропроцессор готов к выполнению следующей команды, указанной в счетчике команд (СК + 2) и т. д.
Следует обратить внимание на особенность записи адреса источника R0. Этот адрес в команде заключен в круглые скобки, что означает, что в регистре R0 хранятся не сами данные, а адрес ячейки памяти, в которой находятся нужные данные.
Итак, компьютер функционирует лишь благодаря программному обеспечению, без которого он бесполезен.
Эволюцию ЭВМ рассмотрим на примере больших универсальных ЭВМ фирмы IBM.
Становление вычислительной техники началось с появления в 1946 г. первой ЭВМ «ЭНИАК» и продолжалось до 1955 г., когда сформировалась архитектура вычислительных машин и был принят принцип модульности, согласно которому ЭВМ конструировались в виде набора отдельных функционально завершенных блоков.
Начиная с 1955 г., в истории развития вычислительной техники прослеживается несколько этапов, связанных прежде всего с развитием элементной и технологической базы, причем каждому такому этапу соответствует свое поколение ЭВМ.
Обобщенным параметром любого компьютера является его вычислительная мощность, определяемая быстродействием и объемом внутренней памяти ЭВМ. Первые ЭВМ:
r ЭНИАК (1946);
r МЭСМ (конструктор — академик С. А. Лебедев, 1951).
 Первое поколение ЭВМ строилось на электровакуумных лампах
(радиолампах) и дискретных радиодеталях. В качестве внутренней памяти
использовались магнитные барабаны. Внешняя память была построена на магнитных
лентах. Информация в машину вносилась с бумажных перфолент и перфокарт.
Выходная информация распечатывалась на бумажном но- сителе.
Первое поколение ЭВМ строилось на электровакуумных лампах
(радиолампах) и дискретных радиодеталях. В качестве внутренней памяти
использовались магнитные барабаны. Внешняя память была построена на магнитных
лентах. Информация в машину вносилась с бумажных перфолент и перфокарт.
Выходная информация распечатывалась на бумажном но- сителе.
29 апреля 1952 г. появилась первая ЭВМ фирмы IBM — IBM 701. В качестве устройства оперативной памяти в ней использовался магнитный барабан. Емкость ОЗУ составляла 20 480 байт, а производительность — 8000 оп./с.
 В ЭВМ второго поколения в качестве элементной базы
использовались полупроводниковые приборы, миниатюрные дискретные
радиодетали и печатный монтаж. Память ЭВМ строилась на магнитных ферритовых
сердечниках.
В ЭВМ второго поколения в качестве элементной базы
использовались полупроводниковые приборы, миниатюрные дискретные
радиодетали и печатный монтаж. Память ЭВМ строилась на магнитных ферритовых
сердечниках.
IBM 360/40 была изготовлена в 1964 г. Для разных моделей она комбинировалась из 19 блоков центрального процессора и 40 типов периферии. Емкость ОЗУ — 256 Кбайт, производительность — 246 тыс. оп./с.
 Третье поколение ЭВМ разрабатывалось уже на базе интегральных
схем и микроминиатюрных ферритовых сердечников диаметром до 0,3 мм. ЭВМ
этого поколения стали еще более экономичными и быстродействующими.
Третье поколение ЭВМ разрабатывалось уже на базе интегральных
схем и микроминиатюрных ферритовых сердечников диаметром до 0,3 мм. ЭВМ
этого поколения стали еще более экономичными и быстродействующими.
IBM 370/145 была изготовлена в 1970 г. В ней впервые применены интегральные схемы с 1400 элементами на одном кристалле. Емкость ОЗУ — 512 Кбайт, производительность — 1,23 млн оп./с.
 В ЭВМ этого поколения, построенного на базе кремниевой
технологии, применяются большие (БИС) и сверхбольшие (СБИС)
интегральные схемы. В машинах этого поколения стали впервые
использоваться микропроцессоры. Степень их интеграции росла
лавинообразно, например, динамика изменения величины памяти на однокристальных
БИС выглядит так:
В ЭВМ этого поколения, построенного на базе кремниевой
технологии, применяются большие (БИС) и сверхбольшие (СБИС)
интегральные схемы. В машинах этого поколения стали впервые
использоваться микропроцессоры. Степень их интеграции росла
лавинообразно, например, динамика изменения величины памяти на однокристальных
БИС выглядит так:
1970 г. — 128 бит;
1978 г. — 64 Кбит;
1982 г. — 228 Кбит; 1984 г. — 1 Мбит.
IBM 370/168 была изготовлена в 1972 г. и являлась одной из самых распространенных моделей. Емкость ОЗУ — 8,2 Мбайт, производительность — 7,7 млн оп./с.
 В ЭВМ
пятого поколения используются как универсальные, так и специализированные сверхбольшие
(СБИС) и ультрабольшие (УБИС) интегральные схемы
широкой номенклатуры. Монтаж УБИС ведется на многослойных печатных платах, в
свою очередь, спрессованных в виде «сэндвича» толщиной до 100 слоев.
В ЭВМ
пятого поколения используются как универсальные, так и специализированные сверхбольшие
(СБИС) и ультрабольшие (УБИС) интегральные схемы
широкой номенклатуры. Монтаж УБИС ведется на многослойных печатных платах, в
свою очередь, спрессованных в виде «сэндвича» толщиной до 100 слоев.
EServer z990 изготовлен в 2003 г. Имеет вес 2000 кг и потребляемую мощность 21 кВт, занимает площадь 2,5 кв. м и имеет высоту 1,94 м. Емкость ОЗУ — 256 Гбайт, производительность — 9 млрд оп./с.
В табл. 2.1 приведены характеристики разных поколений ЭВМ.
Таблица 2.1. Сравнительные характеристики ЭВМ
|
Поколение ЭВМ |
Тип ЭВМ |
Год выпуска |
Объем ОЗУ |
Быстро- действие (оп./с) |
|
1 |
IBM-701 |
1952 |
20,5 Кбайт |
8 тыс. |
|
2 |
IBM-360/140 |
1964 |
256 Кбайт |
246 тыс. |
|
3 |
IBM-360/145 |
1970 |
512 Кбайт |
1,23 млн |
|
4 |
IBM-370/168 |
1972 |
8,2 Мбайт |
7,7 млн |
|
5 |
eServer z990, модель D32 |
2003 |
256 Гбайт |
9 млрд |
В настоящее время достигнуты очень высокие характеристики ЭВМ по быстродействию и объему памяти. Линейные размеры микроэлементов достигли 0,09 мкм (физический предел формирования линий рисунка схемы на кристалле — примерно 0,03 мкм). Рост параметров ЭВМ возможен также за счет улучшения схемотехнических решений и методов размещения микросхем на платах. По мнению некоторых специалистов, кремниевая технология исчерпает себя к 2015 г.
Дальнейший прогресс вычислительной техники возможен с появлением новых носителей информации и совершенствованием принципов работы ЭВМ (в частности с реализацией многоядерности процессоров и параллельного программирования).
На рис. 2.4 представлена классификация программного обеспечения (ПО) для современных персональных компьютеров.
Программное обеспечение условно можно разделить на три больших класса:
r системное ПО; r прикладное ПО;
r инструментальное ПО.
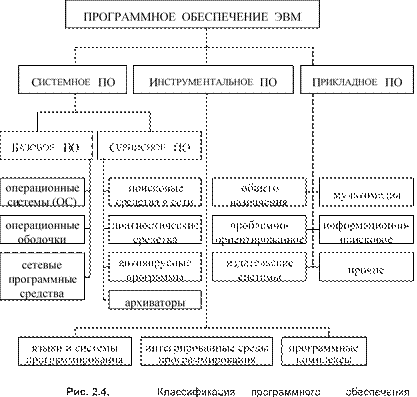
Системное программное обеспечение, в свою очередь, состоит из базового ПО и сервисного ПО.
Базовое ПО поставляется вместе с компьютером и обеспечивает его работоспособность. В состав базового ПО входят операционная система (ОС), операционная оболочка и сетевые программные средства.
Операционная система предназначена:
r для обеспечения запуска и нормальной работы компьютера;
r для обеспечения функционирования других программ на компьютере;
r для диагностики и контроля работоспособности блоков и узлов компьютера;
r для выполнения других вспомогательных технологических процессов.
В настоящее время разработано большое количество ОС, различающихся по возможностям их функционирования: одно- и многопользовательские, одно- и многозадачные, поддерживающие сетевые режимы работы и др. Широкое применение нашли ОС семейств: Windows, Linux, Mac OS, NetWare, OS/2, Solaris, QNX, MS-DOS и др.
Операционная оболочка предназначена для обеспечения более комфортного общения пользователя с ЭВМ. Она снимает проблему управления компьютером путем ввода текстовых команд в командной строке и их запуска на исполнение. В оболочке может быть реализован текстовый или/и графический интерфейс. Например, в ОС MS-DOS в качестве такой оболочки выступает программа Norton Commander, реализующая текстовый интерфейс в виде двух таблиц с каталогами файловой системы, а в ОС Windows и M S интерфейс встроенной операционной оболочки — графический (хотя имеется и оболочка с текстовым интерфейсом, реализуемая программой Windows Commander).
Сетевые программные средства обеспечивают работу компьютера в сети и поддерживают работу всех сетевых служб — электронной почты, обмена файлами, доступа к сайтам, общения между клиентами через Интернет и пр.
Сервисное ПО расширяет возможности компьютера и может приобретаться за отдельную плату или в последующем поставляться через Интернет (для зарегистрированных пользователей).
В настоящее время такие известные операционные системы как Windows XP, Windows Vista, Windows 7, Mac OS и некоторые другие включают в себя все вышеперечисленные компоненты системного ПО, являясь по существу комплексным системным ПО.
Прикладное программное обеспечение предназначено для решения различных задач, возникающих в рамках конкретных предметных областей.
ПО общего назначения обычно комплектуется в пакеты. Например, для ОС Windows выпущен пакет прикладных программ Mirosoft ffie, включающий в себя программные средства для создания текстовых документов (Word), электронных таблиц (Excel), презентаций (PowerPoint), публикаций (Publisher), базы данных (Access), а также для подготовки и редактирования Webдокументов (rote). В этот пакет еще входит ряд дополнительных программных средств: Picture Mer — для просмотра, систематизации и редактирования графики; Document Imi — для просмотра, чтения и распознавания текста в графических документах и факсах; Domet Si — для сканирования многостраничных документов и распознавания текста в графических документах; файлы библиотеки картинок и др.
ПО мультимедиа предназначено для создания и использования (отображения, воспроизведения) двух- и трехмерной графики, анимации, аудио- и видеофайлов. Примерами такого ПО являются широко известные программные комплексы oe Photoshop — для создания и редактирования двухмерной графики, 3D Stio M — для трехмерного моделирования и проектирования, Mromei s — для создания анимаций и мультипликаций. Для обработки и редактирования звука используются такие программы как Nero, Audio Editor Gold, для воспроизведения звука и видео — программы Windows Media Player, QuickTime Player и др.
Проблемно-ориентированное ПО — это, пожалуй, самый распространенный подкласс прикладных программных средств. К нему относятся пакеты программ для управления производством, ведения бухгалтерского учета, управления кадрами, учета материальных ценностей и др.
Значительное количество прикладных программ разработано в качестве информационных систем (см. главу 1 «Информатика и информация»), к которым относятся также информационнопоисковые, издательские и прочие системы.
Инструментальное программное обеспечение предназначено для разработки новых программ и программных комплексов.
Множество различных приложений для компьютера создается с помощью языков и систем программирования.
В процессе становления и развития вычислительной техники возникали и развивались также языки программирования. Некоторые из них затем изменялись, трансформировались, интегрировались с другими, а некоторые — исчезали. Сегодня у программистов имеется богатый арсенал языков программирования на все случаи программистской жизни: ассемблер, Бейсик, C++, Delphi, ortr, Java, Pascal и др. Каждый из этих языков программирования имеет целый ряд модификаций (например, для Бейсика — GW-Basic, QBasic, Visual Basic и др.), которые по возможностям и свойствам существенно отличаются друг от друга.
Языки программирования можно разделить на машинно-зависимые (низкого уровня) и машинно-независимые (высокого уровня). К языкам низкого уровня относятся:
r машинные языки — запись команд в двоичных кодах в виде нулей и единиц;
r машинно-ориентированные языки (ассемблеры), реализующие запись команд в так называемых мнемокодах, соответствующих системе команд конкретного процессора (например, мнемокод «сложить» записан как ADD, мнемокод «очистить» — как DEL и т. д.).
К языкам высокого уровня относятся:
r алгоритмические языки — перевод алгоритмов с языка математики на язык программных кодов;
r процедурно-ориентированные языки — запись программ в виде набора процедур;
r проблемно-ориентированные языки — языки, предназначенные для решения определенного класса задач.
Программа, написанная на языке высокого уровня, не может непосредственно использоваться на компьютере. Она должна пройти этап трансляции исходного кода, записанного на языке высокого уровня, в объектный код, который затем с помощью редактора связей преобразуется в загрузочный модуль, уже пригодный для запуска на компьютере.
Такой процесс осуществляется, например, при написании программы на языке ortr и называется компилированием. В других языках высокого уровня (например, в Бейсике) трансляция исходного кода в исполняемый происходит последовательно для каждой команды (оператора). Такой способ трансляции называется интерпретацией.
Созданная программа должна пройти проверку на пригодность к использованию с помощью отладчика программ. Он позволяет отслеживать ход последовательного исполнения программы, выявлять местонахождение и виды ошибок в программе, давать к ним пояснения для программиста.
Система программирования обычно состоит из:
r языковых средств разработчика программ;
r текстового редактора для написания текста программ;
r компилятора;
r редактора связей;
r отладчика;
r оптимизатора кода программ;
r набора библиотек;
r справочной системы и др.
Интегрированные среды программирования включают в се- бя весь набор средств для их комплексного применения на всех технологических этапах разработки программ. Основное назначение такого инструментария состоит в том, чтобы с его помощью повысить производительность и эффективность труда програм- мистов.
Программные комплексы используются при разработке сложных прикладных информационных систем. Они позволяют автоматизировать весь технологический процесс анализа, проектирования, разработки, отладки и сопровождения таких проектов.
Понятие об элементной базе ЭВМ. Типы транзисторов. Полупроводниковые
Вычислительные устройства, в которых кодирование и обработка информации осуществляются в двоичной системе счисления, называются цифровыми устройствами. Они состоят из множества элементов, которые определенным электрическим воздействием можно перевести в одно из двух устойчивых состояний. Те или иные разновидности цифровых устройств предназначены для запоминания информации, ее арифметической и логической обработки, формирования и усиления сигналов управления, для преобразования и отображения входной и выходной информации и т. д.
Основой большинства элементов современных ЭВМ является транзистор — полупроводниковый прибор, способный преобразовывать электрические сигналы. Существуют два типа транзисторов: биполярный, с двумя взаимодействующими электроннодырочными переходами (рис. 2.5), и униполярный, или полевой
(рис. 2.6).
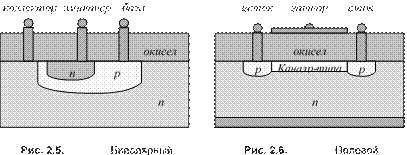
В полевом транзисторе управляющий электрод (затвор) изолирован от тела полупроводника слоем диэлектрика (обычно двуокиси кремния), поэтому такой транзистор также называют МОП- или МДП-транзистором, подчеркивая его структуру: «металл — окисел (диэлектрик) — полупроводник». Из сравнения рис. 2.5 и 2.6 видно, что изготовить МДП-транзистор проще, чем биполярный, т. к. в этом случае на поверхности подложки (полупроводника n-типа) достаточно лишь сформировать две небольшие области полупроводника р-типа и покрыть всю поверхность слоем окисной пленки, в то время как для изготовления биполярного транзистора нужно провести два процесса формирования микрообластей с разной проводимостью.
Интегральная схема (ИС) содержит логический, запоминающий или какой-либо другой элемент цифрового устройства. Конструктивно ИС выполняется на монокристаллической пластинке кремния размером в несколько квадратных миллиметров путем формирования с помощью специальной технологии отдельных микрокомпонентов. Количество элементов в ИС характеризует ее степень интеграции. В соответствии с ним все ИС условно делят на малые (МИС — до 102 элементов на кристалле), средние (СИС — до 103 элементов), большие (БИС — до 104 элементов), сверхбольшие (СБИС — до 106 элементов), ультрабольшие (УБИС — до 109 элементов) и гигабольшие (ГБИС — свыше 109 элементов на кристалле). В настоящее время по МДП-технологии разработаны сверхбольшие и ультрабольшие интегральные схемы (СБИС и УБИС).
Как уже говорилось, конструкция полевого транзистора проще, чем биполярного, поэтому при использовании МДП-транзисторов миниатюризацию элементов ИС осуществить легче. При одинаковой функциональной сложности МДП ИС занимают площадь на кристалле в несколько раз меньше, чем биполярные. Кроме того, благодаря более простой технологии изготовления МДП-приборов можно выпускать ИС с большей функциональной сложностью, чем на биполярных полупроводниках.
Однако МДП ИС имеют и недостатки. Главный из них — сравнительно низкое быстродействие. По этому параметру биполярные ИС превосходят МДП в 10 и более раз, однако потребляемая ими энергия существенно больше, чем для МДП ИС.
Таким образом, каждый тип ИС имеет свои достоинства и недостатки, которые определяют их использование в электронной аппаратуре.
Первый образец транзистора был создан в 1948 г., но затем понадобилось еще 11 лет для поиска требуемых технологических решений, чтобы научиться делать простейшие интегральные схемы на биполярных полупроводниках. В результате родилась так называемая планарная технология, которая к настоящему времени настолько усовершенствована, что по праву считается одной из наиболее изящных технологий, разработанных человечеством.
Технология изготовления ИС включает в себя совокупность целого ряда механических, физических и химических способов обработки различных материалов (полупроводников, диэлектриков, металлов) с применением трех классов физико-химических процессов: удаления, нанесения и перераспределения вещества.
В планарной технологии используются процессы окисления, фотолитографии, диффузии, эпитаксиального наращивания пленок, химического и ионно-плазменного травления и ряд других операций. В частности, для формирования рисунка микросхем (будущих полупроводниковых микроэлементов, соединяющих их проводников и т. д.) используется метод фотолитографии, заключающийся в том, что на поверхность кристалла с нанесенным на нее фоточувствительным слоем через фотошаблон с будущим рисунком микросхемы воздействует пучок ультрафиолетового излучения (с длиной волны 0,1–0,3 мкм), который «выжигает» участки фотослоя между линиями рисунка. Минимальные линейные размеры элементов рисунка достигают при этом 0,3–0,5 мкм.
Наряду с фотолитографией используется электронолитография, позволяющая получать элементы рисунка толщиной до 0,1 мкм, и рентгенолитография с длиной волны излучения 0,003– 0,005 мкм, дающая возможность получать размеры элементов менее 0,1 мкм.
Линейные размеры микроэлементов последних СБИС и УБИС достигли величины порядка 0,09 мкм. По оценкам специалистов верхний предел ширины линий рисунка составит около 0,03– 0,05 мкм. Фактически это физический предел малости рисунка ИС. Столь малые размеры деталей полупроводниковых приборов позволяют на одном кристалле размером 1 см2 разместить сотни миллионов отдельных компонентов электронной схемы.
По планарной технологии ИС обычно изготовляют целыми группами, когда на одной пластине кремния диаметром 150–200 мм одновременно формируются десятки и сотни отдельных ИС. Для размещения схемных деталей ИС средней степени интеграции при этом отводится площадь 2,5×2,5 мм2, для БИС — площадь 6×6 мм2, для СБИС — до 10×10 мм2, а для УБИС свыше 1 см2. После завершения процесса формирования ИС пластина кремния разрезается на отдельные кристаллы, которые затем монтируются в пластмассовые корпуса и проходят тщательный контроль на пригодность схемы к работе.
Все многообразие устройств ЭВМ базируется на ограниченном наборе типовых электронных элементов. Поэтому принципы функционирования даже очень сложного компьютера нетрудно понять, если предварительно разобраться в структуре и в принципах работы базовых электронных элементов, к которым относятся инвертор (ключ), вентиль и триггер.
На рис. 2.7, а представлена схема электронного ключа на биполярном транзисторе, реализующая логическую функцию «НЕ» (отрицание), а на рис. 2.7, б приведено его условное обозначение.
При подаче на вход схемы сигнала низкого уровня (логического 0) транзистор будет заперт, т. е. ток через него проходить не будет, и на выходе будет сигнал высокого уровня (напряжение источника питания Еп, логическая 1). Если же на вход схемы подать сигнал высокого уровня (логическую 1), то транзистор откроется и начнет пропускать электрический ток, так что на его выходе
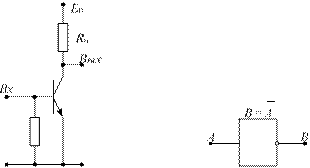
а б
Рис. 2.7. Инвертор
за счет падения напряжения на сопротивлении нагрузки Rн устано вится напряжение низкого уровня (логический 0).Таким образом, данная схема преобразует (инвертирует) сигналы одного уровня в другой, тем самым выполняя логическую функцию «НЕ».
На рис. 2.8, а изображена схема вентиля на биполярных транзисторах, реализующего логическую функцию «И», а на рис. 2.8, б приведено его условное обозначение.

а б
Рис. 2.8. Вентиль «И»
Функция «И» — это логическое умножение: ее результат С равен единице, когда оба аргумента (и А, и В) равны единице.
Если на входы Вх1 и Вх2 поданы сигналы низкого уровня (логические 0), то оба транзистора закрыты, ток через них не проходит, а выходное напряжение на Rн близко к 0. Если на один из входов подано напряжение высокого уровня (логическая 1), то соответствующий транзистор откроется, но другой транзистор останется закрытым, ток через эти транзисторы по-прежнему проходить не будет, а выходное напряжение на Rн по-прежнему будет нулевым. Следовательно, при подаче напряжения высокого уровня лишь на один из транзисторов такая схема не переключается, и на выходе остается напряжение низкого уровня. И только при одновремен ной подаче на оба входа сигналов высокого уровня (логических 1) на выходе мы также получим сигнал высокого уровня: открытые транзисторы практически не оказывают сопротивление току, все напряжение падает на сопротивлении нагрузки Rн, и потенциал на выходе Вых становится высоким.
На рис. 2.9, а приведена схема вентиля на биполярных транзисторах, реализующего логическую функцию «ИЛИ», а на рис. 2.9, б дано его условное обозначение.
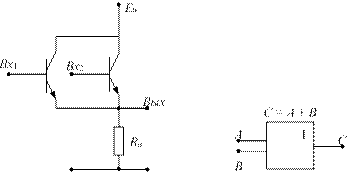
а б
Рис. 2.9. Вентиль «ИЛИ»
Функция «ИЛИ» — это логическое сложение, ее результат С равен единице, если хотя бы один из аргументов (A или B) равен единице.
Здесь транзисторы включены параллельно друг другу. Если оба они закрыты, то их общее сопротивление велико и на выходе будет сигнал низкого уровня (логический 0). Но достаточно подать сигнал высокого уровня (логическую 1) на один из транзисторов (любой), и схема начнет пропускать ток, а на сопротивлении нагрузки Rн установится сигнал высокого уровня (логическая 1).
В разделе, посвященном законам алгебры логики (см. гла- ву 4) показано, что любая сложная логическая функция может быть представлена как комбинация функций «НЕ», «И» и «ИЛИ», так что из инвертора и соответствующих вентилей можно построить электронную логическую схему, выполняющую любое заплани рованное действие. В этом же разделе показано, что вместо трех перечисленных логических функций можно использовать всего одну комбинированную функцию «И-НЕ» или «ИЛИ-НЕ». Для получения вентилей «И-НЕ» и «ИЛИ-НЕ» из «И» и «ИЛИ» достаточно перенести сопротивление нагрузки Rн из эмиттерной цепи в коллекторную (как в схеме инвертора).
Триггером называется электронное устройство с двумя устойчивыми состояниями, одно из которых характеризуется высоким (логическая 1), а второе — низким (логический 0) уровнем выходного сигнала.
Триггер состоит из двух вентилей. На рис. 2.10, а показан триггер, составленный из двух вентилей «ИЛИ-НЕ» (аналогично для этой цели можно использовать и вентили «И-НЕ»), а на рис. 2.10, б — его условное обозначение.
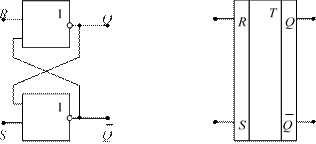
а б
Рис. 2.10. Триггер
Рассмотрим работу этой схемы (соответствующая анимация имеется на диске, прилагаемом к книге). Пусть в начальный момент времени входы R, S и выход Q имеют низкий логический уровень.
Для переключения триггера в состояние Q = 1 необходимо на вход S подать логическую 1. На входе соответствующего вентиля будут действовать входные логические сигналы: 0 (с выхода Q)
и 1 (со входа S). На его выходе возникает инвертированная 1, т. е. 0. Следовательно, через некоторое время ∆τ, в течение которого входной сигнал S = 1 достигнет выхода вентиля, состояние
![]()
выхода Q изменится с 1 на 0.
Теперь на входы второго вентиля будет действовать новая пара
![]()
сигналов: 0 на вход R и 0 с выхода Q . Следовательно, еще через время ∆τ на выходе этого вентиля возникнет инвертированный сигнал 0, т. е. 1.
Таким образом, через время 2∆τ после подачи входного сигнала S = 1 на выходе Q триггера логический 0 изменится на логическую 1.
Следующее переключение триггера произойдет, если на вход R подать сигнал высокого уровня, и т. д.
Триггер может работать бесперебойно лишь с периодом, не меньшим 4∆τ. В современных транзисторных вентилях ∆τ составляет единицы наносекунд (10–9 с), поэтому быстродействие электронных элементов вычислительных устройств очень велико и достигает сотен миллионов переключений в секунду.
Из триггеров (они бывают и других типов, отличающихся от рассмотренного в предыдущем разделе) строятся многие элементы ЭВМ, например регистры. Они предназначены для приема, временного хранения и передачи информации в двоичном коде. Каждый триггер регистра используется для ввода, хранения и вывода одного разряда (бита) двоичного числа.
Регистр, предназначенный для хранения информации, называют накопительным. Существуют также сдвигающие регистры (регистры сдвига), в которых двоичную информацию можно поразрядно перемещать влево и вправо, а также счетные регистры, предназначенные для преобразования десятичных чисел в двоичные и обратно.
На основе рассмотренных ранее базовых элементов строятся различные микросхемы ЭВМ, такие как процессор, память, сумматор, дешифратор, мультиплексор и др.
1. Из каких основных узлов состоит ЭВМ?
2. Компьютер и мобильный телефон содержат одинаковые узлы: микропроцессор, память, устройства ввода/вывода. Есть ли между ними принципиальные отличия? Если есть, то в чем?
3. В чем разница между внутренней и внешней памятью ЭВМ? На какие виды разделяется внутренняя память? Назовите внешние виды памяти?
4. Какие функции в компьютере выполняет микропроцессор?
5. Как осуществляется программный принцип работы компьютера?
6. На какие классы и подклассы разделяется программное обеспечение ЭВМ?
7. Каково назначение и структура системного программного обес- печения?
8. Каково назначение и структура прикладного программного обеспечения?
9. В чем разница между языком и системой программирования?
10. По каким признакам история развития вычислительной техники ассоциируется с поколениями ЭВМ?
11. Почему вычислительная мощность является основным параметром ЭВМ?
12. Каковы ближайшие перспективы развития вычислительной техники?
13. Из каких элементов («кирпичиков») строится компьютер?
14. Чем отличается технология производства элементов вычислительной техники от технологии производства деталей автомобиля?
15. В чем общность и различие базовых электронных элементов?
16. Как устроен триггер и где он используется?
17. Используя табл. 2.1, содержащую сравнительные характеристики ЭВМ, с помощью программы Ee постройте график зависимости вычислительной мощности компьютера от номера поколения ЭВМ.
18. Используя табл. 2.1, с помощью программы Ee постройте зависимость «Изменение основных параметров ЭВМ пяти поколений».
19. В современном
процессоре серии etim на площади кристалла в 3,6 см2 размещается примерно 5 млн транзисторов (n). Считая, что
размеры транзистора по каждой оси равны 15 линиям технологического разрешения
(0,09 мкм). Рассчитайте коэффициент заполнения поверхности кристалла ( K = n / Nmax).
Задание 17
Изменение вычислительной мощности в зависимости от поколения ЭВМ
|
Объем памяти, lgQ, Кбайт |
Быстродействие, lgV, тыс. оп./с |
Вычислительная мощность, lgQ × lgV |
Поколения ЭВМ |
|
1,301029996 |
0,903089987 |
1,174947162 |
1 |
|
2,408239965 |
2,390935107 |
5,757945479 |
2 |
|
2,709269961 |
3,089905111 |
8,371387101 |
3 |
|
3,913813852 |
3,886490725 |
15,21100124 |
4 |
|
8,408239965 |
6,954242509 |
58,4729398 |
5 |
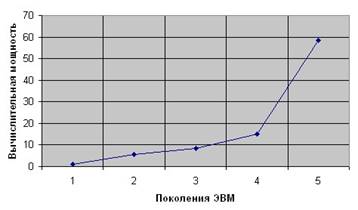
Рис. 2.11. График зависимости вычислительной мощности компьютеров от номера поколения ЭВМ
Задание 18
Изменение основных параметров ЭВМ пяти поколений
|
Объем памяти, lgQ, Кбайт |
Быстродействие, lgV, тыс. оп./с |
|
1,301029996 |
0,903089987 |
|
2,408239965 |
2,390935107 |
|
2,709269961 |
3,089905111 |
|
3,913813852 |
3,886490725 |
|
8,408239965 |
6,954242509 |
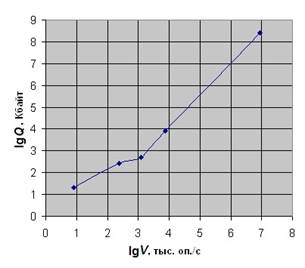
Рис. 2.12. Изменение основных параметров ЭВМ пяти поколений
Задание 19
1. Переведем площадь кристалла из сантиметров в микроны:
3,6 см2 = 360 мм2 = 360 ⋅ 1000 ⋅ 1000 мкм2 = 3,6 ⋅ 108 мкм2.
2. Определим площадь, занимаемую одним транзистором:
3,6 ⋅ 108 : 5 ⋅ 106 = 72 мкм2.
3. Определим размер теоретически возможного транзистора по заданной технологии (0,09 мкм):
(15 ⋅ 0,09)2 = 1,352 = 1,8 мкм2.
Количество таких транзисторов на кристалле будет равно:
3,6 ⋅ 108 : 1,8 = 2 ⋅ 108 штук.
4. Коэффициент заполнения поверхности кристалла равен:
5 ⋅ 106 : 2 ⋅ 108 = 0,025.
Глава 3
Двоичная арифметика
Без знания правил двоичной арифметики нельзя разобраться в особенностях работы ЭВМ.
|
Двоичная арифметика 57
|

Любая информация воспринимается человеком в виде текста, изображений, звуков, осязательных ощущений, запахов и вкусов. Основной поток информации человек получает через зрение.
Текстовая информация осмысленно воспринимается только в том случае, если человек умеет читать и знает язык, на котором написан текст, т. е. знает буквенный и числовой алфавит. В русском языке используются кириллица (33 буквы) и арабские цифры от 0 до 9. В английском языке используются буквы латинского алфавита (26 букв). В японском или китайском языке вместо привычных нам букв используются иероглифы, каждый из которых обозначает целое понятие, и т. д.
Кроме национальных языков, для общения людей разработаны и специальные (профессиональные) языки, например математический язык, нотная грамота, язык электросхем, алгоритмический язык, азбука Морзе и т. д.
В вычислительной технике для записи информации в памяти компьютера или на носителе тоже используется свой язык, состоящий всего из двух элементов (сигналов): наличие сигнала кодируется единицей (1), а его отсутствие — нулем (0).
Математический алфавит, состоящий из двух цифр (0 и 1), называется двоичным и вместе с правилами его использования составляет двоичную систему счисления. В двоичной системе счисления используются две цифры: 0 и 1.
Кроме двоичной, в вычислительной технике применяются и другие системы счисления, являющиеся в каком-то смысле «производными» от двоичной, — восьмеричная, шестнадцатеричная и др. В восьмеричной системе счисления используются восемь цифр: 0, 1, 2, 3, 4, 5, 6 и 7. Шестнадцатеричная система счисления состоит из десяти арабских цифр (от 0 до 9) и первых 6 букв латинского алфавита: A, B, C, D, E, F, которые обозначают числа 10, 11, 12, 13, 14 и 15 соответственно.
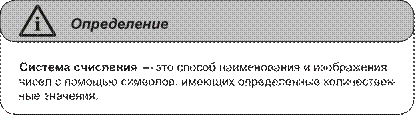
Системы счисления бывают позиционными и непозиционными.
В непозиционной системе счисления цифры не меняют своего количественного значения при изменении места их расположения в числе. Например, в римской непозиционной системе счисления для каждого числа используется некоторый набор базовых символов (I, V, X, L, C, D и M), соответствующих числам 1, 5, 10, 50, 100, 500 и 1000. Остальные значения чисел получаются из базовых путем их сложения (например, XVII = 17) или вычитания (например, IX = 9).
В позиционной системе счисления значение каждой цифры зависит от ее места расположения (позиции, разряда) в числе. Количество цифр в числе определяет его разрядность, а вес того или иного разряда зависит от его позиции в числе. При этом вес каждого последующего разряда в P раз больше предыдущего, где P — это основание позиционной системы счисления.
На практике любое многоразрядное десятичное число записывается без указания веса разрядов.
Развернутая запись чисел в любой позиционной системе счисления имеет вид:
XP = A(N – 1) ⋅ P(N – 1) + A(N – 2) ⋅ P(N – 2) + ∙∙∙
... + A1 ⋅ P1 + A0 ⋅ P0 + A–1 ⋅ P–1 + A–2 ⋅ P–2 + ∙∙∙ + A–S ⋅ P–S, а краткая запись имеет вид:
XP = A(N – 1)A(N – 2) ∙∙∙ A1A0A–1A–2 ∙∙∙ A–S.
Здесь P — основание системы счисления; N — количество разрядов целочисленной части числа; S — количество разрядов дробной части числа; A — цифры, входящие в основание системы счисления.
Например, в наиболее привычной нам десятичной системе счисления краткая и развернутая записи шестиразрядного числа (N = 6) выглядят так:
X10 = 123325,8 =
= 1 ⋅ 105 + 2 ⋅ 104 + 3 ⋅ 103 + 3 ⋅ 102 + 2 ⋅ 101 + 5 ⋅ 100 + 8 ⋅ 10–1.
Следует отметить, что нумерация разрядов в такой записи всегда идет справа налево, начиная с нуля для разряда единиц (для целых чисел). В этом случае вес любого разряда можно получить путем возведения основания системы счисления в степень, значение которой равно номеру этого разряда.
Как уже было сказано, в вычислительной технике широко применяют двоичную систему счисления. К ее достоинствам относятся:
r возможность использования наиболее простой элементной базы микроэлектроники — всего с двумя устойчивыми состояниями;
r возможность использования аппарата булевой алгебры для выполнения логических преобразований информации;
r возможность использования простейших правил арифметики.
Основной недостаток двоичной системы — быстрый рост количества разрядов, необходимых для записи чисел. По этой, а также по некоторым другим причинам, кроме двоичной, применяются также восьмеричная и шестнадцатеричная системы счисления.
В табл. 3.1 приведена запись чисел от 0 до 20 в разных системах счисления.
Таблица 3.1. Примеры чисел в разных системах счисления
|
Основание системы счисления |
|||
|
10 |
2 |
8 |
16 |
|
0 |
0 |
0 |
0 |
|
1 |
1 |
1 |
1 |
|
2 |
10 |
2 |
2 |
|
3 |
11 |
3 |
3 |
|
4 |
100 |
4 |
4 |
|
5 |
101 |
5 |
5 |
|
6 |
110 |
6 |
6 |
|
7 |
111 |
7 |
7 |
|
8 |
1000 |
10 |
8 |
|
9 |
1001 |
11 |
9 |
|
10 |
1010 |
12 |
A |
|
11 |
1011 |
13 |
B |
|
12 |
1100 |
14 |
C |
|
13 |
1101 |
15 |
D |
|
14 |
1110 |
16 |
E |
|
15 |
1111 |
17 |
F |
|
16 |
10000 |
20 |
10 |
|
17 |
10001 |
21 |
11 |
|
18 |
10010 |
22 |
12 |
|
19 |
10011 |
23 |
13 |
|
20 |
10100 |
24 |
14 |
Напомним, что числа в любой системе счисления можно представить в развернутой или краткой форме:
XP = A(N – 1) ⋅ P(N – 1) + ... + A1 ⋅ P1 + A0 ⋅ P0 + A–1 ⋅ P–1 + ... + A–SP–S или
XP = AN – 1 ... A1A0A–1 ... A–S.
При этом справедливо равенство:
XP(A1) = YQ(B1)
или
AN – 1 ... A1A0A–1 ... A–S = BN – 1 ... B1B0B–1 ... B–S,
где A1, B1 — цифры в системах P и Q соответственно.
В частности для перевода числа X из десятичной системы в P-ичную, можно воспользоваться выражением:
X10 = XP = AN – 1 ... A2A1A0A–1A–2 ... A–S.
Вычисления при этом производятся отдельно для целой и дробной частей числа.
Перепишем развернутую формулу для целой части следующим образом:
X10 = A0 + P ⋅ (A1 + P ⋅ (A2 + ... + P ⋅ (A(N – 1)) ...)).
Если теперь нацело разделить число X10 на P, то получится частное и остаток. Остаток будет равен A0, а частное — первому множителю числа P, т. е. A1 + P ⋅ (A2 + ... + P ⋅ (A(N – 1))...). Снова разделив частное на P, получим в остатке A1, а в частном — (A2 + ... + P ⋅ (A(N – 1))...) и т. д. Этот процесс продолжается, пока очередное частное не станет меньше P. Это частное будет старшей цифрой в записи числа: A(N – 1).
Таким образом, путем последовательных делений можно получить все цифры целого числа X10. Отметим, что все эти вычисления производятся по правилам десятичной арифметики.
 Чтобы
преобразовать целое число, записанное в системе P, в число в системе Q,
нужно исходное число разделить на основание системы Q по
правилам P-ичной арифметики и полученные остатки от деления справа
налево записать в виде искомого числа.
Чтобы
преобразовать целое число, записанное в системе P, в число в системе Q,
нужно исходное число разделить на основание системы Q по
правилам P-ичной арифметики и полученные остатки от деления справа
налево записать в виде искомого числа.
Теперь рассмотрим перевод правильной десятичной дроби. Пусть X10 = A–1 ⋅ P–1 + A–2 ⋅ P–2 + ... + A–SP–S. Если умножить это число на P, то получим: X10 ⋅ P = A–1 + A–2 ⋅ P–1 + ... + A–SP–S + 1. Это смешанное число, у которого целая часть равна A–1. Это первая искомая цифра. Дробная часть произведения равна: (A–2 ⋅ P–1 + ... + A–SP–S + 1). Последовательное умножение повторяется до тех пор, пока в дробной части очередного произведения не получится ноль, не будет обнаружена периодичность повторяющихся цифр или не будет исчерпано отведенное для хранения числа количество разрядов.
 Чтобы
преобразовать дробную часть числа, записанную в системе P, в число в
системе Q, нужно исходное число умножить на основание
системы Q по правилам P-ичной арифметики и получаемые целые части
записать в виде искомого числа
Чтобы
преобразовать дробную часть числа, записанную в системе P, в число в
системе Q, нужно исходное число умножить на основание
системы Q по правилам P-ичной арифметики и получаемые целые части
записать в виде искомого числа
П р и м е р ы преобразования чисел из десятичной системы счисления в другие:
|
1. 2710 = X2: |
2. 0,7510 = X2: |
||||||||
|
|
|
|
||||||
|
Ответ: 2710 = 110112. |
Ответ: 0,7510 = 0,112. |
|||||||
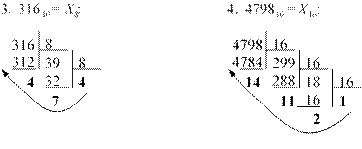
Ответ: 31610 = 4748. Ответ: 479810 = 12BE16.
Для смешанного числа необходимо отдельно преобразовать целую и дробную части числа и соединить их через запятую.
П р и м е р: 27,7510 = 11011,112.
Обратный перевод чисел из двоичной, восьмеричной, шестнадцатеричной или любой другой системы в десятичную проще всего сделать, записав соответствующее число в развернутой форме и подсчитав десятичное значение полученной суммы. Например, для числа в двоичной системе счисления:
110100101,1012 = (1 ⋅ 28 + 1 ⋅ 27 + 0 ⋅ 26 + 1 ⋅ 25 + 0 ⋅ 24 + + 0 ⋅ 23 + 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 + 1 ⋅ 2–1 + 0 ⋅ 2–2 + 1 ⋅ 2–3)10 = = (256 + 128 + 32 + 4 + 1 + 1/2 + 1/8)10 = 421,62510.
Шестнадцатеричное число преобразуется аналогично:
AF016 = 10 ⋅ 162 + 15 ⋅ 161 + 0 ⋅ 160 = 2560 + 240 + 0 = 280010.
Запись чисел в двоичной системе удобна для компьютера, но громоздка для человека. На помощь приходят системы, родственные двоичной — восьмеричная и шестнадцатеричная. Для перехода из двоичной системы счисления прямо в восьмеричную число, записанное в двоичной системе, делится на триады (группы по 3 разряда) справа налево (если нужно, слева дописывается дополнительный ноль).
П р и м е р: 11011100011 = 011 011 100 011.
Заменяя затем каждую триаду восьмеричной цифрой, получаем требуемый результат: 33438.
При переводе двоичного числа в шестнадцатеричное это двоичное число делится на тетрады (группы по 4 разряда), а затем каждая тетрада заменяется одной шестнадцатеричной цифрой.
П р и м е р: (1011 1010 1101)2 = (11 10 13)10 = BAD16.
Любая информация (тексты, изображения, числа, звуки и т. д.), поступающая в ЭВМ, преобразуется в двоичный код.
Например, каждая клавиша на клавиатуре компьютера имеет собственный 8-разрядный двоичный код, так что любая буква латинского и русского алфавита (как прописная, так и строчная), цифра десятичной системы счисления, знак препинания или другой служебный символ имеют свой индивидуальный двоичный код. А поскольку двоичное 8-разрядное число (байт) может обозначать 28 = 256 различных комбинаций, этого вполне достаточно для кодирования сразу двух текстовых алфавитов, цифр и других знаков.
Изображение на экране компьютера представляется в виде растрового расположения точек (пикселов). При этом для монохромных изображений информация о цвете каждой точки хранится в одном 8-разрядном двоичном коде, что позволяет отображать чернобелые изображения с 256 градациями яркости. Для цветных изображений каждый из трех основных цветов также кодируется одним байтом; следовательно, на каждую цветную точку выделяется 3 байта информации (256 × 256 × 256 = 16 777 216 цветовых оттенков).
На кодирование единичного звукового элемента — ноты требуется от нескольких единиц до десятков байтов и т. д.
С учетом сказанного, одна страница текста имеет информационный объем около 3 Кбайт, один цветной экранный кадр содержит уже примерно 3 Мбайт, а 1,5-часовой цветной телевизионный фильм займет объем почти в 300 Гбайт (без учета сжатия видеоинформации).
Рассмотрим теперь более подробно процесс кодирования чисел в компьютере.
Среди чисел, которые мы используем, встречаются натуральные, целые, рациональные и иррациональные.
В вычислительных машинах применяются две формы представления чисел:
r естественная форма, или форма с фиксированной запятой (точкой);
r нормализованная форма, или форма с плавающей запятой (точкой).
В форме с фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой (или точки), отделяющей целую часть от дробной.
П р и м е р ы: 32,54; 0,0036; –108,2.
Эта форма проста и привычна для большинства пользователей, но имеет небольшой диапазон представления чисел и поэтому не всегда пригодна при вычислениях. Если же в результате какой-либо арифметической операции получается число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки, и все дальнейшие вычисления теряют смысл.
В форме с плавающей запятой числа изображаются в виде:
X = ±M × P±r,
где M — мантисса числа (правильная дробь в пределах от 0,1 до 1), r — порядок числа (целое значение), а P — основание системы счисления. Например, приведенные в предыдущем примере числа с фиксированной запятой можно записать в форме с плавающей запятой как 0,3254 × 102, 0,36 × 10–2, –0,1082 × 103. Нормализованная форма представления чисел обеспечивает огромный диапазон их записи и является основной в современных ЭВМ.
Всякое десятичное число, прежде чем оно попадает в память компьютера, преобразуется по схеме:
X10 → X2 → M2 ×10 .2r
После этого осуществляются еще две важные процедуры:
r мантисса вместе с ее знаком заменяется кодом мантиссы с ее знаком;
r порядок числа вместе с его знаком заменяется кодом порядка с его знаком.
Указанные коды двоичных чисел — это образы чисел, с которыми и работают вычислительные устройства.
Каждому двоичному числу можно поставить в соответствие несколько видов кодов.
Прямой код двоичного числа (мантиссы или порядка) образуется по следующему алгоритму:
1. Определить данное двоичное число — оно может быть целым (порядок) или правильной дробью (мантисса).
2. Если это дробь, то цифры после запятой можно тоже рассматривать как отдельное целое число.
3. Если это целое положительное двоичное число, то путем добавления нуля в старший разряд это число превращается в его код. Для отрицательного двоичного числа в его старшем разряде ставится единица.
П р и м е р ы:
r число X2 = –0,1011012 ⇒ код числа Xпр = 1101101;
r число Y2 = +0,11011012 ⇒ код числа Yпр = 01101101.
(Жирным шрифтом выделены знаковые разряды; кроме того, в записи кодов отсутствует индекс системы счисления — «2».)
Обратный код для положительного двоичного числа совпадает с его прямым кодом, а для отрицательного числа нужно во всех разрядах, кроме знакового, нули заменить единицами и наоборот.
П р и м е р ы:
r число X2 = –0,101012 ⇒ Xпр = 110101 ⇒ Xобр = 101010; r число Y2 = + 0,11012 ⇒ Yпр = 01101 = Yобр.
Дополнительный код для положительного числа совпадает с его прямым кодом, а для отрицательного числа образуется путем прибавления 1 к обратному коду.
П р и м е р ы:
r число X2 = –0,100102 ⇒ Xпр = 110010 ⇒ Xобр = 101101 ⇒ Xдоп = 101110;
r число Y2 = + 0,1011 ⇒ Yпр = 01011 = Yобр = Yдоп.
Сложение двоичных чисел, а также вычитание чисел, записанных в обратном или в дополнительном коде, выполняется с использованием обычного правила арифметического сложения многоразрядных чисел, которое распространяется и на знаковые разряды чисел. Различие же в использовании обратного и дополнительного кодов связано с тем, что затем делают с единицей переноса из старшего разряда, изображающего знак числа. При сложении чисел в обратном коде эту единицу надо прибавить к младшему разряду результата, а в дополнительном коде единица переноса из старшего разряда просто игнорируется. Это очевидно, если вспомнить, что дополнительный код получается из обратного как раз прибавлением единицы.
П р и м е р: сложение чисел +18 и –7.
|
|
В обратном коде |
В дополнительном коде |
||
|
Десятичная форма |
+18 |
–7 |
+18 |
–7 |
|
Двоичная форма |
+10010 |
–111 |
+10010 |
–111 |
|
Прямой код |
00010010 |
10000111 |
00010010 |
10000111 |
|
Обратный код |
00010010 |
11111000 |
|
|
|
Дополнительный код |
|
|
00010010 |
11111001 |
|
Сложение |
00010010 + 11111000 |
|
|
00010010 + 11111001 |
|
прибавить → (1)00001010+1 игнорировать → (1)00001011 |
||||
Как видим, и в обратном, и в дополнительном коде результаты сложения совпали и равны 10112 = 1110.
Умножение и деление двоичных чисел в ЭВМ производится в прямом коде, а их знаки используются лишь для определения знака результата. Так же, как и в математике, умножение и деление сводится здесь к операциям сдвига и сложения (с учетом знаков чисел). Полученные коды мантиссы и порядка для каждого числа помещаются в соответствующие ячейки памяти ЭВМ. Для каждой цифры, входящей в код, в ячейке памяти отводится отдельное место. Одна ячейка памяти состоит из 8 бит (1 байта). В современных компьютерах для одного машинного слова выделяются 2 байта, а в самых последних моделях ПК обработка информации ведется двойными словами, содержащими 4 байта. Числа с фиксированной запятой имеют формат одного слова, а числа с плавающей запятой — формат двойного слова.
П р и м е р. Дано число с плавающей запятой –0,625×108. Нужно преобразовать его в машинный код и заполнить 32-разрядную ячейку памяти.
Мантисса числа равна 0,62510 = 0,1012. Поскольку порядок таких чисел может быть как положительным, так и отрицательным, то машинный порядок смещается относительно естественного так, чтобы весь диапазон машинных порядков изменялся от 0 до максимума, определяемого количеством разрядов, выделяемых для размещения кода порядка. Обычно в 32-разрядной ячейке памяти цифры порядка занимают семь разрядов старшего байта, а восьмой разряд используется для фиксации знака числа. Семь двоичных разрядов позволяют разместить диапазон десятичных разрядов от –64 до +63. Если обозначить машинный порядок через R, а естественный — через r, то связь между ними будет такой:
R10 = r10 + 6410.
Для двоичной системы счисления
R2 = r2 + 10000002.
В нашем примере порядок r равен 810 = 10002, следовательно, R2 = 1001000.
В двоичной системе исходное число имеет вид:
–0,101 × 101000.
Запись этого числа в 32-разрядной ячейке памяти будет следующей:
|
|
Знак числа |
Порядок |
Мантисса |
|
|
||||||||||||
|
Номер разряда |
31 |
30 |
29 |
28 |
27 |
26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
... |
1 |
0 |
|
Значение разряда |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
1. Что понимается под системой счисления?
2. В чем заключается разница между непозиционной и позиционной системами счисления?
3. Чем отличается развернутая запись многоразрядного числа от краткой записи?
4. В чем состоят преимущества и недостатки двоичной системы счисления?
5. Как преобразовать целое число, записанное в одной системе счисления, в число в другой системе счисления?
6. Как преобразуется дробная часть числа при переходе из одной системы счисления в другую?
7. Какие существуют формы представления чисел в компьютере?
8. Каково представление двоичных чисел в прямом, обратном и дополнительном кодах?
9. Как производится сложение, вычитание, умножение и деление двоичных чисел?
10. В каком формате представляются в памяти ЭВМ действительные числа?
11. Запишите десятичное число 25 в двоичной, восьмеричной и шестнадцатеричной системах счисления.
12. Переведите числа из одной системы счисления в другую:
101102 ⇒ Х10
2910 ⇒ Х2
4910 ⇒ Х8
1268 ⇒ Х10
13. Переведите числа из одной системы счисления в другую:
1101010012 ⇒ Х16
11110001112 ⇒ Х8
378 ⇒ Х3
14. Переведите числа из одной системы счисления в другую:
77658 ⇒ Х16
D4F16 ⇒ Х2
2315 ⇒ Х8
21023 ⇒ Х8
15. Переведите числа из одной системы счисления в другую:
1101,112 ⇒ Х10
45,78 ⇒ Х10
3D,A16 ⇒ Х10
О т в е т: 2510 = 110012; 2510 = 318; 2510 = 1916.
Р е ш е н и е.
1. Делим число 25 на 2:
25 : 2 = 12 (остаток 1).
Снова делим число 12 на 2:
12 : 2 = 6 (0).
Снова делим число 6 на 2:
6 : 2 = 3 (0).
Наконец, делим число 3 на 2:
3 : 2 = 1 (1).
Двоичное число составится из остатков, записанных от конца к началу, т. е. 1(1)(0)(0)(1) ⇒ 11001.
Ответ: 110012.
2. Делим число 25 на 8:
25 : 8 = 3 (остаток 1).
Восьмеричное число составится так: 3(1) ⇒ 31.
Ответ: 318.
3. Делим число 25 на 16:
25 : 16 = 1 (остаток 9).
Шестнадцатеричное число составится так: 1(9) ⇒ 19.
Ответ: 1916.
О т в е т: 101102 ⇒ Х10 = 22
2910 ⇒ Х2 = 11101
4910 ⇒ Х8 = 61 1268 ⇒ Х10 = 86
Р е ш е н и е.
1. Запишем двоичное число в развернутой форме и вычислим его сумму:
101102 = 1 ⋅ 24 + 0 ⋅ 23 + 1 ⋅ 22 + 1 ⋅ 21 + 0 ⋅ 20 = 16 + 4 + 2 = 22.
Ответ: Х10 = 22.
2. Делим число 29 на 2:
29 : 2 = 14 (остаток 1).
Снова делим число 14 на 2:
14 : 2 = 7 (0).
Снова делим число 7 на 2:
7 : 2 = 3 (1).
Наконец, делим число 3 на 2:
3 : 2 = 1 (1).
Двоичное число составится из остатков, записанных с конца до начала, т. е. 1(1)(1)(0)(1) ⇒ 11101.
Ответ: Х2 = 11101.
3. Делим число 49 на 8:
49 : 8 = 6 (остаток 1).
Восьмеричное число составится так: 6(1) ⇒ 61.
Ответ: Х8 = 61.
4. Запишем восьмеричное число в развернутой форме и вычислим его сумму:
1268 = 1 ⋅ 82 + 2 ⋅ 81 + 6 ⋅ 80 = 64 + 16 + 6 = 86.
Ответ: Х10 = 86.
О т в е т: 1101010012 ⇒ Х16 = 1A9
11110001112 ⇒ Х8 = 1707
378 ⇒ Х3 = 1101
Р е ш е н и е.
1. При переводе двоичного числа в шестнадцатеричное это двоичное число сгруппируем по 4 разряда справа налево. Если в самой левой группе остается менее четырех разрядов, то слева дополним ее недостающими нулями. Затем каждую группу заменим одним шестнадцатеричным числом:
110101001 ⇒ 0001 1010 1001 ⇒ 1А9.
Ответ: Х16 = 1A9.
2. При переводе двоичного числа в восьмеричное это двоичное число сгруппируем по 3 разряда справа налево. Если в самой левой группе остается менее трех разрядов, то слева дополним ее недостающими нулями. Затем каждую группу заменим одним восьмеричным числом:
1111000111 ⇒ 001 111 000 111 ⇒ 1707.
Ответ: Х8 = 1707.
3. Делим число 37 на 3:
37 : 3 = 12 (остаток 1).
Снова делим число 12 на 3:
12 : 3 = 4 (0).
Наконец, делим число 4 на 3:
4 : 3 = 1(1).
Троичное число составится из остатков, записанных с конца до начала, т. е. 1(1)(0)(1) ⇒ 1101.
Ответ: Х3 = 1101.
О т в е т: 77658 ⇒ Х16 = FF5
D4F16 ⇒ Х2 = 110101001111
2315 ⇒ Х8 = 102
21023 ⇒ Х8 = 101
Р е ш е н и е.
1. Запишем исходное восьмеричное число в двоичном коде, присвоив каждой цифре ее 3-разрядный двоичный аналог:
7765 ⇒ 111 111 110 101.
Преобразуем 3-разрядные группы в 4-разрядные и затем каждую группу запишем в шестнадцатеричном коде:
111 111 110 101 ⇒ 1111 1111 0101 ⇒ FF5.
Ответ: Х16 = FF5.
2. Запишем исходное шестнадцатеричное число в двоичном коде, присвоив каждой цифре ее 4-разрядный двоичный аналог:
D4F ⇒ 1101 0100 1111 ⇒ 1101010011112.
Ответ: Х2 = 110101001111.
3. Запишем пятеричное число в развернутой форме и вычислим его сумму:
2315 = 2 ⋅ 52 + 3 ⋅ 51 + 1 ⋅ 50 = 50 + 15 + 1 = 6610.
Теперь преобразуем полученное десятичное число в искомое восьмеричное по правилу последовательного деления. Делим число 66 на 8:
66 : 8 = 8 (остаток 2).
Снова делим число 8 на 8:
8 : 8 = 1 (0).
Восьмеричное число составится из остатков, записанных с конца до начала, т. е. 1(0)(2) ⇒ 102.
Ответ: Х8 = 102.
4. Запишем троичное число в развернутой форме и вычислим его сумму:
21023 = 2 ⋅ 33 + 1 ⋅ 32 + 0 ⋅ 31 + 2 ⋅ 30 = 54 + 9 + 2 = 6510.
Теперь преобразуем полученное десятичное число в искомое восьмеричное по правилу последовательного деления. Делим число 65 на 8:
65 : 8 = 8 (остаток 1).
Снова делим число 8 на 8:
8 : 8 = 1 (0).
Восьмеричное число составится из остатков, записанных с конца до начала, т. е. 1(0)(1) ⇒ 101.
Ответ: Х8 = 101.
О т в е т: 1101,112 ⇒ Х10 = 13,75
45,78 ⇒ Х10 = 37,875 3D,A16 ⇒ Х10 = 61,625
Р е ш е н и е.
1. Вычисления будем проводить отдельно для целой и дробной частей смешанного числа.
Запишем двоичное число в развернутой форме и вычислим его сумму:
11012 = 1 ⋅ 23 + 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 = 8 + 4 + 1 = 13.
Теперь преобразуем дробную часть двоичного числа в искомое десятичное по правилу последовательного умножения дробной части на основание искомой системы счисления, т. е. на 1010 (это основание десятичной системы счисления в двоичной записи), выделяя при этом целые цифры как значащие в десятичной записи:
0,11 ⋅ 1010 = 111,10 0,10 ⋅ 1010 = 101,0.
Дробная часть стала нулевой, а целые числа 1112 и 1012 в десятичной записи равны соответственно числам 7 и 5. Таким образом, 0,112 ⇒ 0,7510.
Ответ: смешанное число Х10 = 13,7510.
2. Вычисления будем проводить отдельно для целой и дробной частей смешанного числа.
Запишем восьмеричное число в развернутой форме и вычислим его сумму:
458 = 4 ⋅ 81 + 5 ⋅ 80 = 32 + 5 = 37.
Теперь преобразуем дробную часть восьмеричного числа в искомое десятичное по правилу последовательного умножения дробной части на основание искомой системы счисления, т. е. на 12 (это основание десятичной системы счисления в восьмеричной записи), выделяя при этом целые цифры как значащие в десятичной записи:
0,78 ⋅ 12 = 8,68
(потому, что в восьмеричной системе 2 ⋅ 7 равно не 14, а 16 — одна восьмерка плюс одна шестерка). Получившуюся дробную часть снова умножаем на 12:
0,68 ⋅ 12 = 7,48
(по той же причине, т. к. 2 ⋅ 6 равно не 12, а 14 в восьмеричной системе). Оставшуюся дробную часть снова умножаем на 12:
0,48 ⋅ 12 = 5,08.
Дробная часть стала нулевой, а целые числа имеют значения
8, 7, 5. Итак,
0,78 = 0,87510.
Рассмотренное преобразование можно осуществить проще. Величина 0,78 в развернутой форме будет иметь вид:
7 ⋅ 8–1 = 7 : 8 = 0,87510.
Таким образом,
0,78 = 0,87510.
Ответ: смешанное число X10 = 37,87510.
3. Вычисления будем проводить отдельно для целой и дробной части смешанного числа.
Запишем шестнадцатеричное число в развернутой форме и вычислим его сумму:
3D = 3 ⋅ 161 + D ⋅ 160 = 48 + 13 = 61.
Теперь преобразуем дробную часть: величина A16 равна 10 единицам в этой системе счисления, следовательно, в десятичной системе счисления величина А равна частному от деления:
10 : 16 = 0,62510.
Таким образом,
0,А16 = 0,625.
Ответ: смешанное число X10 = 61,62510.
Глава 4
Бинарная лоГика
|
Двоичная арифметика 79
|

Основы логики как науки были заложены великим древнегреческим ученым Аристотелем (IV в. до н. э.), а со средины XIX в. благодаря трудам англичанина Джорджа Буля (1815–1864), шотландца Огастеса (Августа) де Моргана (1806–1871), немца Готлоба Фреге (1848–1925), итальянца Джузеппе Пеано (1858–1932) и других возникла математическая логика, которая перевела на точный язык математики все прежние достижения логики, дала мощный толчок ее дальнейшему развитию и существенно повысила уровень строгости и доказательности математики в целом.
Основными объектами логики являются логические высказывания — предложения, которые могут быть либо истинными, либо ложными.
Логический подход заключается в том, что истинность высказывания устанавливается на основе истинности других высказываний, т. е. без обращения к фактам, к содержанию этих высказываний, а чисто формально, с помощью рассуждений. Такой подход основан на выявлении и использовании логических связей между высказываниями, входящими в рассуждение. Анализ различных логических связей и методы построения на их основе правильных логических рассуждений — это и есть предмет логики.
Разработан специальный математический аппарат — алгебра логики. Эта алгебра во многом похожа на обычную алгебру (арифметическую): в алгебре логики основными объектами являются формулы, состоящие из букв, знаков операций и скобок. Буквы обозначают переменные, которые могут принимать различные числовые значения. С формулами можно производить действия двух видов: вычисления и преобразования. Каждая формула задает некоторую функцию, количество аргументов (переменных) этой функции равно количеству различных букв в формуле.
Отличия алгебры логики заключаются в следующем. В формулах алгебры логики переменные являются логическими (двоичными), т. е. принимающими только два значения — ложь и истина, которые обозначаются обычно 0 и 1. Знаки операций обозначают логические операции (логические связки). Каждая формула задает логическую функцию — функцию от логических переменных, которая тоже может принимать только два логических значения — ложь и истина.
Любую логическую функцию f (x1, ..., xn) можно задать в виде таблицы, в левой части которой записаны все возможные наборы значений ее аргументов х1, ..., хn, а правая часть содержит столбец значений функции, соответствующих этим наборам. Количество строк в такой таблице равно 2n — числу возможных наборов значений аргументов, т. е. количеству различных комбинаций длины n из нулей и единиц.
n
Количество различных функций от n переменных равно 22 — числу возможных расстановок нулей и единиц в столбце с 2n строками.
Таблица функции f (х) от одной переменной содержит всего две строки, а самих функций одной переменной — четыре:
|
x |
f (x) |
|
x |
f (x) |
|
x |
f (x) |
|
x |
f (x) |
|
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
|||
|
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
Генератор 0 f (x) = x f (x) = ¬x Генератор 1
(повторение) (отрицание)
Таблица функции f (х1, х2) от двух переменных содержит четыре строки, а самих функций от двух переменных — шестнадцать
n
(22 = 24 =16). Наиболее важные из них — следующие:
|
|
|
Дизъюнкция Конъюнкция
(ИЛИ) (И)
|
|
|
Импликация Эквивалентность
|
x1 |
x2 |
x1 ⊕ x2 |
|
0 |
0 |
0 |
|
0 |
1 |
1 |
|
1 |
0 |
1 |
|
1 |
1 |
0 |
Сложение по модулю 2
(исключающее ИЛИ)
Указанные пять функций соответствуют логическим связкам ИЛИ (дизъюнкция, логическое сложение), И (конъюнкция, логическое умножение), ЕСЛИ ... ТО (импликация), ЕСЛИ И ТОЛЬКО ЕСЛИ (эквивалентность, равнозначность) и ЛИБО, ... ЛИБО (исключающее ИЛИ, неравнозначность, сложение по модулю 2). Кроме этого, часто употребляются еще две функции двух переменных — ИЛИ-НЕ (стрелка Пирса) и И-НЕ (штрих Шеффера):
|
x1 |
x2 |
x1 ↓ x2 |
|
x1 |
x2 |
x1 | x2 |
|
0 |
0 |
1 |
0 |
0 |
1 |
|
|
0 |
1 |
0 |
0 |
1 |
1 |
|
|
1 |
0 |
0 |
1 |
0 |
1 |
|
|
1 |
1 |
0 |
1 |
1 |
0 |
Стрелка Пирса Штрих Шеффера
(ИЛИ-НЕ) (И-НЕ)
Приведенные 11 таблиц логических функций называются таблицами истинности этих функций. Значение любой логической формулы, содержащей знаки этих функций, на заданном наборе значений переменных можно вычислить, используя эти таблицы. Пусть, например, функция f (х1, х2, х3) задана формулой:
(¬х1 ∨ х2) → х1 ∧ х3.
Вычислим эту функцию на наборе х1 = 1, х2 = 1, х3 = 0. (С точки зрения логики нужно определить значение истинности сложного высказывания при условии, что составляющие его простые высказывания х1 и х2 истинны, а х3 — ложно.) Подстановка значений в формулу дает запись:
(¬1 ∨ 1) → 1 ∧ 0 = 1 → 0 = 0.
Точно также можно вычислить эту формулу и для остальных семи возможных наборов значений х1, х2, х3, полностью восстановив таблицу истинности этой функции.
Существуют наборы логических функций, с помощью которых можно выразить любые другие логические функции. Такие наборы называются функционально полными наборами, или базисами. Наиболее известный и изученный базис — это набор И, ИЛИ, НЕ (конъюнкция, дизъюнкция, отрицание). Множество всех логических функций, на котором определены эти три операции, называется булевой алгеброй. Операции и формулы булевой алгебры также часто называют булевыми операциями или булевыми формулами.
Функциональная полнота булевой алгебры означает, что переход от табличного задания к булевой формуле всегда возможен. Метод перехода заключается в следующем:
r для каждого набора значений переменных х1, ..., хn из таблицы истинности, на котором функция f (х1, ..., хn) равна 1, выписывается конъюнкция всех переменных (знак ∧ , & или ⋅);
r над теми переменными, которые в этом наборе равны 0, ставятся отрицания (знак ¬ либо надчеркивание);
r все такие конъюнкции соединяются знаками дизъюнкции (∨ или +).
В дальнейшем мы будем пользоваться следующими обозначениями: отрицание (¬), дизъюнкция (+) и конъюнкция (⋅).
Полученная формула называется совершенной дизъюнктивной нормальной формой (СДНФ) логической функции f (х1, ..., хn). СДНФ для каждой функции единственна. Это означает, что две различные СДНФ одной функции могут отличаться только порядком конъюнкций и расстановкой переменных в конъюнкциях. Для примера СДНФ функции импликации (см. таблицу истинности в разд. «Алгебра логики» ранее в этой главе) имеет вид:
(¬х1 ⋅ ¬х2) + (¬х1 ⋅ х2) + (х1 ⋅ х2).
Обычно СДНФ — это весьма громоздкая формула. Упрощение формул в булевой алгебре (как и в любой другой алгебре) производится на основе эквивалентных преобразований, опирающихся на основные законы (эквивалентные соотношения), которые в каждой алгебре — свои.
В булевой алгебре эти законы — следующие:
1. Ассоциативность конъюнкции и дизъюнкции:
х1 ⋅ (х2 ⋅ х3) = (х1 ⋅ х2) ⋅ х3 = х1 ⋅ х2 ⋅ х3; х1 + (х2 + х3) = (х1 + х2) + х3 = х1 + х2 + х3.
2. Коммутативность конъюнкции и дизъюнкции:
x1 ⋅ x2 = x2 ⋅ x1; x1 + x2 = x2 + x1.
3. Дистрибутивность конъюнкции относительно дизъюнкции: х1 ⋅ (х2 + х3) = (х1 ⋅ х2) + (х1 ⋅ х3).
4. Дистрибутивность дизъюнкции относительно конъюнкции: х1 + (х2 ⋅ х3) = (х1 + х2) ⋅ (х1 + х3).
5. Идемпотентность (отсутствие степеней и коэффициентов): х ⋅ х = х; х + х = х.
6. Закон двойного отрицания:
¬ ¬х = х.
7. Свойства констант 0 и 1: х ⋅ 1 = х; х ⋅ 0 = 0; х + 1 = 1; х + 0 = х;
¬0 = 1; ¬1 = 0.
8. Правила де Моргана:
¬(х1 ⋅ х2) = ¬х1 + ¬х2;
¬(х1 + х2) = (¬х1 ⋅ ¬х2).
9. Закон противоречия:
х ⋅ ¬х = 0.
10. Закон исключенного третьего:
х + ¬х = 1.
Два последних закона указывают, что при любых аргументах высказывание х ⋅ ¬х всегда ложно, а высказывание х + ¬х всегда истинно.
Законы 1, 2, 3, 7 показывают, что свойства конъюнкции очень похожи на свойства умножения, поэтому ее часто называют логическим умножением.
Из законов 6 и 8 следует, что, используя отрицание, можно выразить дизъюнкцию через конъюнкцию и наоборот:
х1 + х2 = ¬ ¬(х1 + х2) = ¬(¬х1 ⋅ ¬х2);
х1 ⋅ х2 = ¬ ¬(х1 ⋅ х2) = ¬(¬х1 + ¬х2).
Это означает, что наборы ИЛИ-НЕ и И-НЕ также явля- ются функционально полными. Отсюда следует, что базисом может служить одиночная функция «стрелка Пирса» или «штрих Шеффера».
С помощью основных законов можно вывести соотношения, часто используемые в булевой алгебре. Например, соотношение х + х ⋅ у = х (поглощение) выводится путем последовательного применения законов 7, 3, 7, 7:
х + х ⋅ у = х ⋅ 1 + х ⋅ у = х ⋅ (1 + у) = х ⋅ 1 = х.
Аналогично выводятся формулы
х ⋅ у + х ⋅ ¬у = х (склеивание по у)
и
х + ¬х ⋅ у = х + у (*).
Основные функции двух переменных, записанные в табличном виде в разд. «Алгебра логики» ранее в этой главе, представляются в булевой алгебре (через дизъюнкцию, конъюнкцию и отрицание) следующими формулами:
|
r импликация: |
x1 → x2 = ¬x1 + x2; |
|
r эквивалентность: |
x1 ∼ x2 = x1 ⋅ x2 + ¬x1 ⋅ ¬x2; |
|
r сложение по модулю 2: |
x1 ⊕ x2 = x1 ⋅ ¬x2 + ¬x1 ⋅ x2; |
|
r штрих Шеффера: |
x1 | x2 = ¬(x1 ⋅ x2) = ¬x1 + ¬x2; |
|
r стрелка Пирса: |
x1 ↓ x2 = ¬(x1 + x2) = ¬x1 ⋅ ¬x2. |
Эквивалентные соотношения, приведенные выше, можно получить с помощью СДНФ. Например, для формулы импликации СДНФ будет иметь вид:
¬х1 ⋅ ¬х2 + ¬х1 ⋅ х2 + х1 ⋅ х2.
Применяя законы 3, 10 и формулу (*), получим:
¬х1 ⋅ ¬х2 + ¬х1 ⋅ х2 + х1 ⋅ х2 = ¬х1(¬х2 + х2) + х1 ⋅ х2 =
= ¬х1 + х1 ⋅ х2 = ¬х1 + х2.
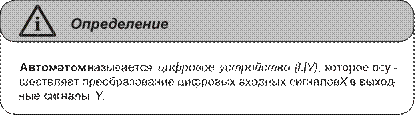
Для формирования цифровых выходных сигналов используются ЦУ двух классов.
1. ЦУ, выходные сигналы Y которых в некоторый момент времени зависят только от совокупности (комбинации) сигналов Х, присутствующих на их входах в тот же момент времени, и не зависят от входных сигналов, поступивших в предшествующие моменты времени. ЦУ этого класса «не помнят» предыстории поступления сигналов на их входы. Такие ЦУ принято называть комбинационными цифровыми устройствами (КЦУ), или однотактными автоматами.
2. ЦУ, выходные сигналы Y которых в некоторый момент времени определяются не только комбинациями входных сигналов Х, воздействующих в тот же момент времени, но и сигналами, поступившими на входы в предшествующие моменты времени. В составе таких ЦУ обязательно присутствуют элементы памяти, внутреннее состояние которых отражает предысторию поступления последовательности входных сигналов. Подобные ЦУ принято называть последовательностными цифровы- ми устройствами (ПЦУ), или многотактными (конечными) автоматами.
Правила функционирования КЦУ могут быть заданы различными способами: словесно, таблицами истинности, булевыми выражениями. Реализация КЦУ предполагает выбор определенных логических элементов из заданного набора и их соединение таким образом, чтобы обеспечивалась зависимость цифровых выходных сигналов от входных в соответствии с заданными правилами функционирования.
Ранее было указано, что в базисный набор элементарных логических элементов входят три логические функции — И, ИЛИ, НЕ. В качестве базиса также могут выступать одиночные функции: ИЛИ-НЕ (стрелка Пирса) и И-НЕ (штрих Шеффера). Графическое обозначение вышеперечисленных логических элементов приведено на рис. 4.1.
В процессе проектирования любого устройства приходится выполнять ряд действий, которые могут быть отнесены к задачам анализа и синтеза.
Синтез КЦУ предусматривает построение структурной схемы устройства, т. е. определение состава необходимых логических элементов и соединений между ними, при которых обеспечивается преобразование входных цифровых сигналов в выходные в соответствии с заданными условиями работы устройства. В процессе синтеза обычно подразумевается необходимость минимизации аппаратных затрат на реализацию устройства.
A
|
& |
A B |
1 |
|
![]() X A
X A
B
И ИЛИ НЕ
![]()
![]() A
A
B
ИЛИ-НЕ И-НЕ
Рис. 4.1. Графические обозначения базисных логических элементов
Таким образом, при конструировании автомата нужно выполнить следующие действия:
1. Задать словесное описание автомата.
2. Рассмотреть работу автомата на уровне «черного ящика», т. е. определить количество его входов и выходов.
3. Составить таблицу его работы.
4. Записать структурную формулу автомата.
5. Начертить структурную (функциональную) схему.
П р и м е р.
1. Словесное описание автомата.
Для оповещения зрителей на соревнованиях по тяжелой атлетике (штанга) используется периодически загорающийся транспарант «Вес взят правильно». Транспарант освещается, получив сигнал от автомата, который обрабатывает сигналы, поступившие к нему от судей. Судей трое, один из них — старший. Вес считается взятым правильно при единодушном мнении всех трех судей или двух из них, но при условии, что один из судей — старший. Пометим его буквой А. Если по мнению судьи вес взят правильно, то он нажимает кнопку, расположенную на его столе, тем самым на один из входов автомата подается сигнал 1.
2. Располагая словесным описанием автомата, можно представить его в виде «черного ящика»: автомат имеет три входа, по которым поступают сигналы от судей, и один выход, по которому автомат выдает сигнал освещения транспаранта (рис. 4.2).
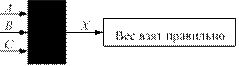
Рис. 4.2. Представление автомата в виде «черного ящика»
3. Составим таблицу работы автомата. Полученная таблица задает автомат табличным способом.
|
A |
B |
C |
Х |
|
1 |
1 |
1 |
1 |
|
1 |
1 |
0 |
1 |
|
1 |
0 |
1 |
1 |
|
1 |
0 |
0 |
0 |
|
0 |
1 |
1 |
0 |
|
0 |
1 |
0 |
0 |
|
0 |
0 |
1 |
0 |
|
0 |
0 |
0 |
0 |
Из таблицы видно, в каких случаях Х = 1 (тогда транспарант будет освещен).
4. Структурная формула автомата имеет вид:
![]()
X = ABC + ABC + ABC = AB + AC = A B( + C).
5. Соответствующая структурная (функциональная) схема представлена на рис. 4.3.

Рис. 4.3. Функциональная схема автомата
Возможная структура ПЦУ представлена на рис. 4.4.
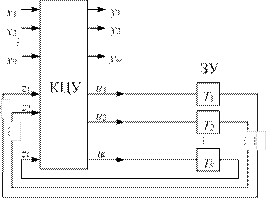
Рис. 4.4. Возможная структура ПЦУ
ПЦУ состоит из комбинационного цифрового устройства (КЦУ) и запоминающего устройства (ЗУ). Последнее представляет собой совокупность простейших элементов памяти (триггеров) Т1, Т2, ..., Тk, на которые воздействуют сигналы U = {u1, u2, ..., uk} (структура и принцип действия триггера приведены в разд. «Триггер» главы 2 «Устройство ЭВМ»).
Под воздействием сигнала ui элемент Ti может перейти в одно из двух состояний: 0 или 1. Состояние элемента Ti отображается сигналом Zi. Совокупность сигналов Z = {z1, z2, ..., zk} отображает состояние ПЦУ.
Комбинационное цифровое устройство, входящее в состав ПЦУ, представляет собой устройство, схема которого описывается булевыми функциями Y = F (X, Z), U = H (X, Z). ПЦУ работает под воздействием входных сигналов Х, которые поступают в моменты времени t = 0, 1, 2, ... В момент времени t = 0 ПЦУ находится в начальном состоянии. При этом Z (t) принимает некоторое начальное значение Z (0) = {z1(0), z2(0), ..., zk(0)}.
При поступлении в последующие моменты времени сигналов X (t) в ПЦУ формируются выходные сигналы Y (t) и сигналы U (t), воздействующие на запоминающие элементы. В результате ПЦУ переходит в некоторое состояние Z (t), и тем самым фиксируется воздействие входных сигналов X (t) в момент времени t. Темп работы ПЦУ определяется темпом поступления входных сигналов.
Итак, в ПЦУ каждому набору входных сигналов соответствует однозначный набор выходных сигналов, т. е. реализуется некоторое отображение. Это отображение однозначно определяется заданием функции переходов δ и функции выходов λ автомата.
Функция переходов определяет состояние автомата z(t) по входному сигналу x(t) и состоянию в предыдущий момент времени z(t – 1):
z(t) = δ (z(t – 1), x(t)).
Функция выходов λ устанавливает зависимость выходного сигнала y(t) от тех же переменных:
y(t) = λ (z(t – 1), x(t)).
Конечные автоматы задаются таблицами переходов и выходов с помощью графов или аналитически.
П р и м е р задания автомата в форме таблиц переходов и выходов:
Таблица переходов Таблица выходов
|
Входной сигнал |
Состояние |
|
Входной сигнал |
Состояние |
||
|
z0 |
z1 |
z0 |
z1 |
|||
|
x1 |
z1 |
z1 |
x1 |
y1 |
y2 |
|
|
x2 |
z0 |
z0 |
x2 |
y2 |
y2 |
|
Новые состояния автомата определяются на пересечении строк (входные сигналы) и столбцов (предшествующие состояния). В таблице выходов на пересечении строк и столбцов находятся выходные сигналы.
Граф этого автомата (рис. 4.5) состоит из узлов, поставленных в соответствие отдельным состояниям автомата. Дуги между узлами показывают переходы автомата из одного состояния в другое под воздействием входных сигналов. На каждой дуге указываются входной и выходной сигналы. Дуги, замкнутые на тот же самый узел, указывают, что, получив повторно прежний сигнал, автомат не меняет своего состояния.
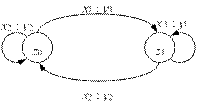
Рис. 4.5. Граф конечного автомата
Используя подобный граф или таблицы, можно задавать автомат и в виде аналитической записи.
Таким образом, таблицы переходов и выходов (граф или аналитическая запись) дают полное описание закона функционирования автомата. Задавая произвольное входное слово в виде последовательности входных сигналов и пользуясь таблицами переходов и выходов, можно определить соответствующее выходное слово автомата.
П р и м е р. На ленте конвейера одна за другой движутся в произвольном порядке детали типа А и В. Требуется сконструировать автомат, который сможет комплектовать из этих деталей упорядоченные тройки АВА, АВА, АВА, ..., ABA.
Конструирование автомата начинается с анализа его словесного задания. Автомат прежде всего должен выбрать из подносимых ему конвейером деталей деталь А (первую в тройке), сбрасывая все ненужные детали В на вспомогательный конвейер, который эти детали возвращает вновь на главный конвейер в конец очереди. Первая деталь А регистрируется автоматом, и затем автомат начнет «вылавливать» вторую деталь — В, сбрасывая очередные детали типа А на вспомогательный конвейер. Пропустив деталь В, автомат помнит о том, что прошла уже пара деталей АВ, и ожидает третью деталь в комплектуемой тройке — деталь А. Пропустив ее, автомат начинает все сначала.
Автомат, запоминая что-то, приобретает соответствующее состояние. Состояния конструируемого автомата будем обозначать так:
r а0 — исходное состояние или состояние перед началом комплектации следующей тройки;
r а1 — состояние после регистрации первой детали А;
r а2 — состояние автомата, который укомплектовал пару АВ.
Как только будет укомплектована тройка АВА, автомат из состояния а2 перейдет в состояние а0 и т. д.
На основе словесного описания автомата-сортировщика построим его граф-схему (рис. 4.6) и таблицу:
|
|
Входы автомата |
Выходы из памяти |
Входы в память |
S |
Примечание |
|||
|
A |
B |
X1 |
X2 |
Y1 |
Y2 |
|||
|
a0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
Смена состояния а0 на а1 |
|
0 |
1 |
0 |
0 |
0 |
0 |
1 |
Сброс детали В |
|
|
a1 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
Сброс детали А |
|
0 |
1 |
0 |
1 |
1 |
1 |
0 |
Смена состояния а1 на а2 |
|
|
a2 |
1 |
0 |
1 |
0 |
1 |
0 |
0 |
Смена состояния а2 на а0 |
|
0 |
1 |
1 |
0 |
0 |
0 |
1 |
Сброс детали В |
|
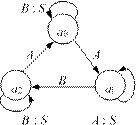
Рис. 4.6. Граф-схема автомата (к примеру)
Из схемы (см. рис. 4.6) видно, что начальное состояние а0 сменяется состоянием а1 под воздействием сигнала А; состояние а1 — состоянием а2 под воздействием сигнала В и, наконец, состояние а2 — начальным состоянием под воздействием сигнала А. Если в состоянии а0 автомат получит сигнал В, то состояние автомата не изменится и он выработает сигнал S — сигнал сброса детали В на вспомогательный конвейер. Эти же действия осуществит автомат, если «увидит» деталь А в состоянии а1 и деталь В — в состоянии а2.
На основании разработанного графа можно определить структуру ЗУ. Поскольку автомату надо помнить три состояния, то достаточно иметь два элемента памяти для записи этих состояний.
Двоичные коды этих состояний: а0 — 00, а1 — 01, а2 — 10.
Основное назначение нашего автомата — комплектовать упорядоченные тройки, своевременно сбрасывая на вспомогательный конвейер ненужные детали. Сбрасывает он их по сигналу S = 1, формирующемуся под влиянием сигналов A, B, X1, X2, т. е. S = F
(A, B, X1, X2).
С помощью таблицы можно составить структурные формулы:
![]() S = ABX X1 2 + ABX X1 2 + ABX X1 2;
S = ABX X1 2 + ABX X1 2 + ABX X1 2;
Y1 = ABX X1 2 + ABX X1 2;
Y2 = ABX X1 2 + ABX X1 2.
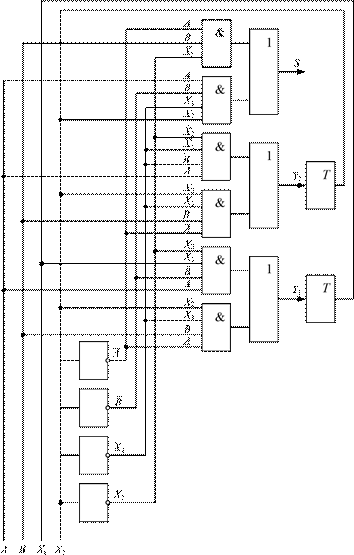
Рис. 4.7. Функциональная схема автомата
Упростим выражение для S, группируя первый и третий члены функции:
![]() S = ABX X1 2 + ABX X1 2 + ABX X1 2 =
S = ABX X1 2 + ABX X1 2 + ABX X1 2 =
= ABX2(X1 + X2) + ABX X1 2 = ABX2 + ABX X1 2.
Используя полученные структурные формулы:
![]() S = ABX2 + ABX X1 2,
S = ABX2 + ABX X1 2,
Y1 = ABX X1 2 + ABX X1 2,
Y2 = ABX X1 2 + ABX X1 2,
построим функциональную схему автомата в базисе «И», «ИЛИ», «НЕ» (рис. 4.7).
На компакт-диске для этой темы есть анимация, в которой демонстрируется порядок построения функциональной схемы автомата. Вначале рисуются логические элементы «И» для выше- указанных структурных формул, далее элементы суммирования «ИЛИ», затем изображаются ячейки памяти «Т» и вспомогательные элементы «НЕ». Наконец, рисуются соединительные линии между элементами схемы и вписываются соответствующие надпи- си. (Примечание: для S логические входы расположены сверху вниз, для Y1, Y2 — снизу вверх.)
1. Что представляет собой логика как наука? Какие проблемы она рассматривает?
2. В чем состоит отличие алгебры логики от алгебры арифметики? Что такое логические переменные и логические функции?
3. Назовите логические функции одной переменной и представьте их табличное значение.
4. Назовите основные логические функции двух переменных и представьте их табличное значение.
5. Что такое таблицы истинности?
6. Приведите примеры функционально полного набора логических функций. Как составить формулу логической функции в виде совершенной дизъюнктивной нормальной формы (СДНФ)?
7. Назовите основные законы (эквивалентные соотношения) булевой алгебры.
8. Как с помощью СДНФ можно преобразовать логические формулы из табличной формы в аналитическую?
9. Дайте определение цифрового автомата. Каковы различия между однотактными и многотактными (конечными) цифровыми автоматами?
10. Как осуществляется разработка однотактного автомата?
11. Опишите структуру и принцип действия многотактного автомата.
12. Какое из трех выражений эквивалентно сложному высказыва-
![]() нию (A+
B) (⋅ A
+ B + C) : а) (A+ C)⋅B;
нию (A+
B) (⋅ A
+ B + C) : а) (A+ C)⋅B;
б) (A+ C)⋅B;
в) AC + B ?
13.. Какие два из четырех высказываний эквивалентны:
а) A B⋅ + C;
![]() б) (A
+ B)⋅C;
б) (A
+ B)⋅C;
в) (A + B)⋅C;
г) A B⋅ +C ?
![]()
14. Структурная формула автомата имеет вид: X = A+ B . Начерти- те его функциональную схему в базисе «стрелка Пирса», а также в базисе «И», «НЕ».
![]()
15. Структурная формула автомата имеет вид: X = AB + AB . Начертите его функциональную схему в базисе «штрих Шеффера».
16. Структурная формула логической функции «эквивалентность»
![]()
имеет вид: X1 : X2 = X1 ⋅ X2 + X1 ⋅ X2 . Начертите функциональную схему в базисе «ИЛИ», «НЕ».
![]()
17. Структурная формула автомата имеет вид: X A B= + . Начертите его функциональную схему в базисе «штрих Шеффера».
18. На рис. 4.8 приведена функциональная схема. Составьте структурную формулу устройства.
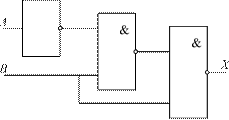
Рис. 4.8. Функциональная схема (к заданию 18)
Задание 12
Р е ш е н и е.
Упростим сложное высказывание:
(A+ B) (⋅ A + B + C) =
![]() = A A⋅ + A B⋅ + A C⋅ + A B⋅ + B B⋅ + B C⋅ .
= A A⋅ + A B⋅ + A C⋅ + A B⋅ + B B⋅ + B C⋅ .
В соответствии с законами булевой алгебры, A A⋅ всегда равно
![]()
![]()
0, а B B⋅ всегда равно B . Группируя теперь второй и пятый члены развернутого выражения, получим:
![]()
B ⋅(A+1) + A C⋅ + A B⋅ + B C⋅ .
А + 1 всегда равно 1, поэтому объединим теперь первый и третий члены полученного выражения:
![]()
B ⋅(1+ A) + A C⋅ + B C⋅ .
Далее сгруппируем снова первый и третий члены выражения:
![]()
B ⋅(1+ C) + A C⋅ = B + A C⋅ .
Что и требовалось доказать.
Можно решить задачу проще, воспользовавшись законом поглощения:
![]()
B + X B⋅ = B,
![]() где Х — любая
логическая переменная. Перепишем развернутое выражение с учетом того, что A A⋅ = 0 , а B B B⋅
= :
где Х — любая
логическая переменная. Перепишем развернутое выражение с учетом того, что A A⋅ = 0 , а B B B⋅
= :
![]() A B⋅ + A C⋅ + A B⋅ + B + B C⋅ .
A B⋅ + A C⋅ + A B⋅ + B + B C⋅ .
Переменная B последовательно поглощает первый, третий и
![]()
пятый члены выражения, в результате остается A C⋅ + B .
Ответ: выражение (в) эквивалентно сложному высказыванию
![]()
(A+ B) (⋅ A + B + C) .
Задание 13
Р е ш е н и е.
![]()
Будем сравнивать первое высказывание ( A B⋅ + C ) с другими высказываниями.
Сравнение начнем между первым и вторым высказываниями. Применим правило де Моргана ко второму высказыванию:
![]()
(A + B)⋅C = (A + B)⋅C = (A + B) +C = (A B⋅ ) +C = (A B⋅ ) + C.
Очевидно, они не эквивалентны (второе высказывание отрицает первое).
Далее сравним первое и третье высказывания. Дважды применим к третьему высказыванию правило де Моргана:
![]()
(A + B)⋅C = (A + B) +C = A B⋅ +C = A B⋅ +C.
Видим, что эти высказывания эквивалентны.
Сравним теперь первое и четвертое высказывания. Дважды применим к четвертому высказыванию правило де Моргана:
![]()
A B⋅ + C = A B C⋅ ⋅ = (A + B)⋅C = (A + B)⋅C .
Видим, что они не эквивалентны.
Ответ: эквивалентны высказывания (а) и (в).
Задание 14
Р е ш е н и е.
В базисе «стрелка Пирса» (логическое значение «ИЛИ-НЕ») функциональная схема показана на рис. 4.9, а, в базисе «И», «НЕ» — на рис. 4.9, б.

а б
Рис. 4.9. Функциональная схема к заданию 14
Задание 15
Р е ш е н и е.
В базисе «штрих Шеффера» (логическое значение «И-НЕ») функциональная схема показана на рис. 4.10. При этом исходная структурная формула была преобразована с помощью правила де Моргана:
![]() A
A
B
A
B
Рис. 4.10. Функциональная схема к заданию 15
Задание 16
Р е ш е н и е.
В базисе «ИЛИ», «НЕ» функциональная схема показана на рис. 4.11. При этом исходная структурная формула была преобразована с помощью правила де Моргана:
![]()
X1 : X2![]() X1 X2 X1 X2 X1 X2 X1 X2
X1 X2 X1 X2 X1 X2 X1 X2
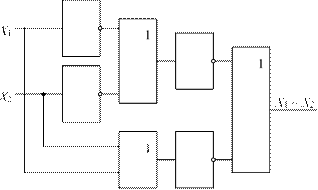
Рис. 4.11. Функциональная схема к заданию 16
Задание 17
Р е ш е н и е.
В базисе «штрих Шеффера» (логическое значение «И-НЕ») функциональная схема показана на рис. 4.12. При этом исходная структурная формула была преобразована с помощью правила де Моргана:
![]()
X = A+ B = A+ B = A B⋅ .
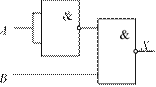
Рис. 4.12. Функциональная схема к заданию 17
Задание 18
Р е ш е н и е.
Структурная формула составляется последовательно слева направо, затем к ее предварительной записи применяется правило де Моргана:
![]()
X = A B B⋅ ⋅ = A B⋅ + B = A B⋅ + B.
Глава 5
ИнформацИонные сИстемы
|
Двоичная арифметика 105
|
Понятие «система» относится к основополагающим понятиям, используемым как в науке, так и в обыденной жизни. По литературным источникам сегодня известно свыше пятисот различных определений этого понятия, за которыми кроются серьезные разночтения, теоретические и методологические несогласованности. Одно из наиболее общих определений этого термина приведено в философском словаре.
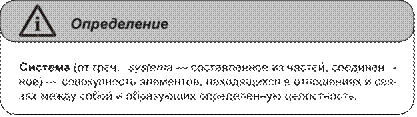
В толковом словаре иностранных слов это понятие расшифро вывается шире:
1. Множество закономерно связанных друг с другом элементов (предметов, явлений, взглядов, знаний и т. д.), представляющее собой определенное целостное образование, единство.
2. Порядок, обусловленный планомерным, правильным расположением частей в определенной связи, строгой последовательностью действий (например, система в работе, принятый, установившийся распорядок чего-либо).
3. Форма, способ устройства, организации чего-либо (например, государственная система, избирательная система).
4. Общественный строй (например, капиталистическая система, социалистическая система).
5. Совокупность хозяйственных единиц, учреждений, родственных по своим задачам и организационно объединенных в единое целое.
6. Совокупность тканей, органов, их частей, представляющих собой определенное единство и связанных общей функцией (например, нервная система, сердечно-сосудистая система).
7. Техническое устройство, конструкция (например, оружие новой системы).
8. В метрологии — система единиц (например, международная система единиц — СИ, физическая система единиц — СГС (см — г — с)).
Очевидно, что толкования этого понятия в пунктах 2–8 являются частным случаем пункта 1.
В недавнем прошлом наука и техника занимались простыми системами, состоящими из сравнительно небольшого числа элементов. Однако с развитием таких наук, как кибернетика, теоретическая информатика, вычислительная техника, искусственный интеллект и др., стали изучаться большие и сложные системы. К таким системам прежде всего можно причислить разработки в области ракетно-космической техники, термоядерного и страте гического вооружения, самолетостроения, кораблестроения, глобальные электросистемы, системы навигации, транспортные системы, а также микроэлектронные и радиоэлектронные изделия, системы программного обеспечения и др.
В современной науке существуют два взгляда на теорию систем. Одними признается объективность существования систем. Другими — существование лишь объектов, которые с целью их изучения удобно представлять в виде систем. С точки зрения первых, поддерживающих общую теорию систем, если реально существуют взаимодействия между объектами, то реально существуют и отвечающие им системы. Порой кажется, утверждают они, что исследователи сами конструируют системы. Это представляется им потому, что существующее, наблюдаемое число элементов ничтожно мало по сравнению с числом систем, которые состоят из этих элементов. Исследователь реального мира не конструирует системы, а отбирает из существующих те, которые ему интересны, нужны для решения его задачи.
Наука, занимающаяся вопросами, связанными с системами разной природы, называется общей теорией систем. Она изучает поведение абстрактных систем с целью обнаружения основных свойств их поведения. Эта теория призвана определить, объяснить, каким образом из отдельных элементов образуется сложное единство целого, новая сущность. Переход от свойств элементов к свойствам системы представляет важнейшую задачу теории систем.
В 1968 г. концепцию общей теории систем предложил австрийский биолог Людвиг фон Берталанфи (1901–1972). Он отмечал, что в современной науке «повсюду возникают проблемы организованной сложности». Справиться с этой проблемой классическая наука не в состоянии, поэтому должна быть создана «общая теория систем в узком смысле, пытающаяся вывести из общего определения понятия „система как комплекс взаимодействующих компонентов“ ряд понятий, характерных для организованных целых» (Берталанфи Л., 1969).
Любая система строго и однозначно определяется ее структурой и функциями входящих в нее элементов. В теории систем функция (от лат. functio — исполнение) имеет иной смысл, чем в математике и означает совокупность воздействий, влияний одно го элемента на другой, ведущих к получению некоторого определенного результата. Структура системы представляет собой организованную совокупность связей между ее элементами (подсистемами), которые рассматриваются безотносительно к процессам, происходящим в этих связях. Можно считать, что сами связи относятся к структуре, а процессы в таких связях, воздействия, которые по ним осуществляются, — к функциям.
В основании общей теории систем лежит постулат структурнофункционального изоморфизма объектов и явлений природы: если структура одной системы и внешние функции ее элементов изоморфны структуре другой системы и внешним функциям ее элементов, то внешние свойства этих систем неразличимы в области их изоморфизма.
Этот постулат имеет в теории систем не меньшее значение, чем законы сохранения в физике или аксиомы в математике. Он является (вместе с другими постулатами) основой, базой для логического, доказательного развертывания теории. Этот постулат позволяет объяснить единство закономерностей природы, относящихся к объектам, которые нам кажутся непохожими и независимыми друг от друга. Наблюдаемый изоморфизм реальных систем является основой и логическим следствием приведенного постулата.
Система в целом способна модифицировать свойства элементов, но сами внешние свойства системы определяются внутренними свойствами, структурой и функциями элементов. Воздействия целого на свои элементы — это рефлексия свойств самих элементов, и ничего более.
Все системы можно разделить на три класса: простые, большие и сложные системы. При этом сложная система может и не быть большой, а большая — может не быть сложной, хотя часто большие системы оказываются сложными, и наоборот.
Если все возможные проявления системы сводятся к сумме проявлений ее элементов, то такая система является простой, несмотря на то, что число ее элементов может быть достаточно велико. Каждый из элементов системы имеет свои свойства и характер поведения в зависимости от собственного состояния и внешних условий.
Для описания простых систем традиционно применяются мето ды анализа, состоящие в последовательном расчленении системы на подсистемы и построении моделей все более простых подсистем. Таковым в своей основе является метод математического моделирования, в котором модели описываются в форме уравнений, а предсказание поведения системы основывается на их решении.
Большие системы — это такие системы, в которых число состояний, определяемых состояниями элементов или взаимосвязями между элементами, комбинаторно велико или несчетно. Это существенно, это наделяет систему специфическими свойствами и накладывает ряд ограничений на исследования таких систем. Например, перебор (сравнение вариантов на основе перебора) в больших системах оказывается принципиально невозможным.
Для больших систем требуются специфические методы исследования и синтеза. Одним из таких методов является декомпозиция системы, разбиение ее на перекрывающиеся области — подсистемы. Существуют рациональные формальные процедуры декомпозиции и методы автоматической оптимальной по некоторому критерию декомпозиции больших систем.
В сложных системах их поведение и свойства не сводятся к простой сумме свойств отдельных компонентов. При вычленении компонентов могут быть потеряны принципиальные свойства, а при добавлении компонентов возникают качественно новые свойства системы. Модель сложной системы, основанная на принципах анализа, будет неадекватной изучаемой системе, поскольку при разбиении системы на составляющие ее компоненты теряются ее качественные особенности. Сложные системы не могут быть выражены, описаны на языке классической математики, на языке формул, языке аналитических структур. Можно различать структурную и функциональную сложность системы.
Возможным выходом из положения является построение модели на основе синтеза компонентов. Основным принципом информационного моделирования является принцип «черного ящика». В противоположность аналитическому подходу, при котором моделируется внутренняя структура системы, в синтетическом методе «черного ящика» моделируется внешнее функционирование системы. С точки зрения пользователя модели структура системы спрятана в черном ящике, который имитирует поведен ческие особенности системы. Кибернетический принцип «черного ящика» использует параметрический класс базисных функций или уравнений, а сама модель синтезируется путем выбора параметров из условия наилучшего соответствия решений уравнений поведению системы. При этом структура системы никак не отражается в структуре уравнений модели.
Функционирование системы в рамках синтетической модели описывается чисто информационно, на основе данных экспериментов или наблюдений над реальной системой. Как правило, информационные модели проигрывают формальным математическим моделям по степени «объяснимости» выдаваемых результатов, однако отсутствие ограничений на сложность моделируемых систем определяет их важную практическую значимость.
Главное оружие общей теории систем — это формализация. Под формализацией понимают построение теории или какойлибо объектной области знания в таком виде, который допускает использование математических (строгих) методов исследования. Формализация — это отображение результатов мышления в точных понятиях.
Но формализация знания — это не просто математизация, это процесс, который требует перестройки самой математики, новых представлений и новых методов в области математики. Под ее влиянием при формализации системных отношений складывается понимание математики как науки об абстрактных структурах, законах их поведения и взаимосвязях между ними.
Наибольшая ценность современной математики проявляется в том, что она выражает внутреннюю организацию явлений и процессов природы в виде объектов и отношений. Для того чтобы к реальному объекту можно было приложить методы математики, нужно выделить его основные, существенные свойства и описать с помощью математики отношения между этими свойствами.
Такая формализация характерна для феноменологического, внешнего описания объекта исследования. Она используется во многих классических науках. Там, где связи между объектами и процессами незначительны, такой формализации оказывается достаточно, но в тех случаях, когда исследователь встречается
со сложными и большими системами, классическая математика дает сбои, отказывает, и приходится искать иные способы формализации. В этом случае на помощь приходят моделирование и теория алгоритмов.
В теории систем, как уже отмечалось ранее, существует постулат изоморфизма. Из двух изоморфных систем одна является моделью по отношению ко второй системе — оригиналу, и наоборот. Таких изоморфных систем может быть множество.
Теория систем утверждает, что никаких других средств, кроме моделирования, для качественного, эффективного описания больших и сложных систем не существует. Вот почему теория систем и ее прикладные дисциплины так тесно связаны с моделированием. Модель представляет собой главный, решающий инструмент системных исследований.
Роль моделирования в исследовании и синтезе больших и сложных систем многозначна. Например, математическое моделирование в теории систем подразумевает построение вначале формальными методами и средствами абстрактного объекта, изофункционального исследуемому объекту, а затем лишь применение математических методов количественного и качественного анализа. (Более подробно модели рассматриваются в главе 6 «Информационные модели»).
Мы обнаружили, что в общей теории систем любой объект, явление, процесс в окружающем нас мире рассматривается как система, состоящая из комплекса взаимодействующих компонентов. Следовательно, в мире существует великое множество систем, характер которых определяется структурой и взаимодействием составляющих их элементов.
Если в качестве элементов системы выступает информация (точнее — данные), то такая система будет называться информационной системой.
Естественно, понятие «информационная система» истолковывается также весьма многообразно в зависимости от смысла, который вкладывается в понятие «информация». В докомпьютерные времена под информационной системой понималась любая организационная структура, имевшая дело с обработкой и хранением информации. Примерами таких структур являлись библиотеки, всевозможные справочные службы, редакции газет и журналов и т. д. С появлением компьютеров традиционные информационные системы существенно изменились и, кроме того, появились принципиально новые информационные системы на основе использования современных информационных и коммуникационных технологий.
Далее приводится несколько характерных определений понятия «информационная система».
![]() Информационная система
— организационно упорядоченная совокупность документов (массивов документов) и
информационных технологий, в том числе с использованием средств вычислительной
техники и связи, реализующих информационные процессы. (Федеральный закон «Об
информации, информатизации и защите информации».)
Информационная система
— организационно упорядоченная совокупность документов (массивов документов) и
информационных технологий, в том числе с использованием средств вычислительной
техники и связи, реализующих информационные процессы. (Федеральный закон «Об
информации, информатизации и защите информации».)
А вот одно из распространенных определений понятия «информационная система»:
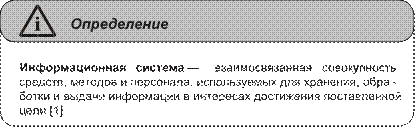
Однако персонал в состав информационной системы включать нецелесообразно, поскольку разработанная и отлаженная информационная система вполне функционирует и без присутствия человека. Поэтому более корректной будет такая формулировка:
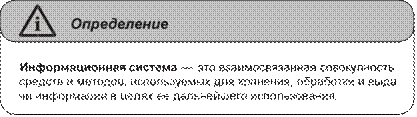
Структурно информационная система состоит из информационного, математического, программного, технического и организационного обеспечения (рис. 5.1).
Информационное обеспечение
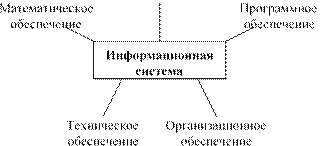
Рис. 5.1. Структура информационной системы
Информационное обеспечение — это банк данных, блок расшифровки запросов и блок поиска.
Математическое и программное обеспечение — это совокупность математических методов, моделей, алгоритмов и программ.
Техническое обеспечение — это комплекс технических средств: компьютеры (устройства сбора, накопления, обработки, передачи и вывода информации), устройства передачи данных и линий связи и т. д., а также документация на них и на технологические процессы обработки данных.
Организационное обеспечение — это совокупность методов и средств, регламентирующих взаимодействие пользователей с техническими средствами системы.
Различные типы информационных систем были рассмотрены в разд. «Структура информатики» главы 1 «Информатика и информация».
1. Информатика: Учебник / Под ред. Н. В. Макаровой. — М.: Финансы и статистика, 1999.
Из предыдущего раздела становится ясно, что информационные системы (ИС), как своеобразное программно-компьютерное отражение окружающего нас объектного мира, весьма многообразны. В связи с этим классифицировать их можно по разным признакам:
r по используемой технической базе;
r по степени автоматизации;
r по структурированности задач;
r по функциональному назначению и др.
Простейшие ИС функционируют на одном компьютере — персональном (ПС), мини-ЭВМ, большой ЭВМ.
Более сложные ИС работают на базе локальной сети. Эти ИС, как правило, обслуживают отдельные учреждения, организации, предприятия. Информация в такой системе может передаваться по сети между отдельными пользователями и подразделениями. Общедоступные данные ИС могут храниться на разных узлах (серверах) локальной сети.
Наиболее сложные ИС работают в глобальных компьютерных сетях, объединяющих множество локальных сетей, распределенных в разных географических точках региона, страны или частях мира. Примерами таких ИС могут быть системы продажи авиа- и железнодорожных билетов, сбора и анализа данных о погодных условиях для прогноза погоды, разные службы Интернета и др.
В зависимости от степени управления ИС можно разделить на ручные, автоматизированные и автоматические.
Все информационные системы докомпьютерного периода были ручными. Характерными примерами могут служить различные каталоги в библиотеках, архивы отделов кадров предприятий и организаций, телефонные справочники и др.
Автоматизированные ИС (АИС) обязательно используют в своем составе аппаратно-программный комплекс (на базе ЭВМ), с помощью которого человек получает доступ к информационному банку данных.
На рис. 5.2 представлена структура АИС, в состав которой входят: банк данных, блок расшифровки запросов, блок поиска, блок пополнения и коррекции банка данных.
В банке данных хранится большая по объему информация о какой-либо области человеческих знаний. Территориально этот банк может быть распределенным. Примером может служить сеть библиотек, находящихся в разных городах страны, связанных между собой системой межбиблиотечного обмена. Для пользователя этот банк представляется как единое хранилище информации, куда он может обратиться с запросом. Например, запросом может быть требование на нужную книгу, оформленное на специальном бланке.
В АИС запросы обрабатываются с помощью специальных компьютерных программ в блоке расшифровки запросов. Его устройство зависит от выбранного языка запросов. Оно достаточно просто, если запросы жестко фиксированы. Если же язык запросов близок к естественному языку, блок может быть достаточно сложным.
Блок Банк
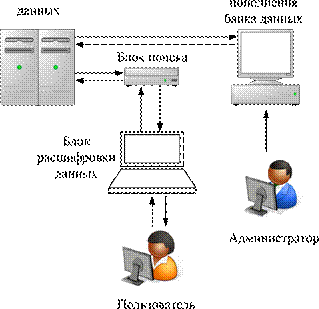
Рис. 5.2. Структура автоматизированной информационной системы
После расшифровки запроса формируется поисковое предписание, представляющее задание для процедуры поиска в бан- ке данных. Поиск в банке данных осуществляется блоком поиска. Найденная информация выдается потребителю в удобной для него форме.
Банк данных требует постоянного обновления, пополнения и чистки. Для этого используется специальный входной канал, которым пользуется ответственный за банк данных.
В настоящее время АИС являются наиболее распространенным типом информационных систем и используются как в управлении (АСУ, АСУТП), так и в новых разработках (САПР), научных исследованиях (АСНИ), обучении (АОС).
Автоматические ИС выполняют все операции по обработке информации без участия человека. Устройства на их основе называют автоматами. С развитием науки и технологий автоматы все шире внедряются на производстве, в быту, в научных исследованиях и пр.
Любая ИС предназначена для решения определенного круга задач. При решении таких задач возникают проблемы, связанные с формальным математическим и алгоритмическим описанием решаемых задач. От степени формализации зависит эффективность работы всей системы, а также уровень автоматизации, определяемый степенью участия человека при принятии решения на основе получаемой информации. Чем точнее математическое описание задачи, тем выше возможности компьютерной обработки данных, тем меньше степень участия человека в процессе ее решения. Это и определяет степень автоматизации задачи.
Различают три типа задач, для которых создаются ИС: структурированные (формализуемые), неструктурированные (неформализуемые) и частично структурированные.
Структурированную задачу можно выразить в форме математической модели, имеющей точный алгоритм решения. Целью использования ИС для решения структурированных задач является полная автоматизация их решения, т. е. сведение роли человека к нулю.
Для неструктурированной задачи описать ее математическую модель и разработать алгоритм весьма затруднительно.
Возможности использования такой ИС ограничены.
Следует отметить, что полностью структурированных или совершенно неструктурированных задач существует сравнительно немного. Большинство практически значимых задач решаются с помощью частично структурированных ИС. Все АИС относятся к этой категории решаемых задач.
Различные ИС применяются в разных областях человеческой деятельности для решения соответствующих прикладных задач. В соответствии с этим можно выделить (см. рис. 1.1):
r АСНИ — автоматизированные системы для научных исследований;
r САПР — системы автоматизированного проектирования;
r АИС — автоматизированные информационные системы (ин- формационно-справочные, информационно-поисковые и т. д.);
r АСУ — автоматические системы управления; r АОС — автоматизированные обучающие системы;
r ЭС — экспертные системы и др.
1. Что такое система?
2. Сформулируйте основные положения общей теории систем.
3. В чем принципиальное различие между простыми, большими и сложными системами?
4. Что такое принцип «черного ящика» в информационном моделировании сложной системы?
5. Какова роль формализации и моделирования при изучении сложных систем?
6. Проанализируйте представленные в тексте определения понятия «информационная система». Есть ли между ними существенные различия или противоречия?
7. По каким признакам можно классифицировать информационные системы?
8. Перечислите известные вам информационные системы по функциональному назначению.
Глава 6
ИнформацИонные моделИ
|
Двоичная арифметика 121
|
Понятие «модель» столь же многозначно, как и понятие «система». Приведем некоторые толкования этого термина в словарях:
r схема, изображение или описание какого-либо явления или процесса в природе и обществе;
r тип, марка, образец конструкции чего-либо;
r воспроизведение предмета в увеличенном или уменьшенном виде;
r предмет изображения в искусстве;
r образец какого-либо изделия для серийного производства;
r образец предмета, служащий для изготовления формы при отливке или воспроизведении в другом материале
и т. д.
В общем случае под моделью некоторого объекта понимается другой объект (реальный, знаковый или воображаемый), отличный от исходного, который обладает существенными для целей моделирования свойствами и в рамках этих целей полностью заменяет исходный объект. Еще короче можно сформулировать определение этого понятия следующим образом:
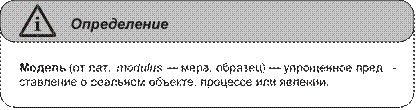
Соответственно, можно дать определение и понятию «моделирование»:
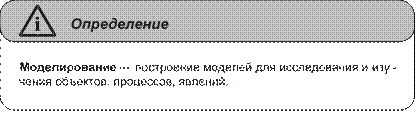
Модель предназначена для изучения объекта путем его упрощения и выделения только тех параметров, которые существенны для целей изучения. Современные научные знания сформированы и опираются на множество моделей, созданных и используемых в процессе познания мироздания. Степень соответствия разработанных моделей реальным объектам проверяется экспериментально — опытом, на практике. Каждая наука формирует свой тип моделей: физические, математические, химические, биологические, а также психологические, педагогические, лингвистические и др. Эти модели могут существенно различаться по назначению, структуре, формам представления, целевым функциям, однако все они в какой-то мере являются неким подобием оригинала.
Классификацию моделей можно провести по разным признакам. Например, по цели моделирования, по способу моделирования, по степени формализации, по степени неопределенности, по временнóй зависимости и т. д. А можно все многообразие моделей разделить на три класса:
r материальные;
r знаковые;
r умозрительные.
К материальным относятся модели, имеющие как ту же природу, что и объект моделирования, так и иную материальную природу. Например, для исследования электрических потерь в проводниках используется гидродинамическая модель течения жидкости в тонких трубках, а с помощью резонансного электрического контура исследуются диссипативные характеристики упругих пружин и т. д.
Знаковые модели можно поделить еще на три типа: описательные, математические и информационные.
Описательные модели представляются на обычном (профессиональном) языке общения людей. Это может быть инструкция по использованию какого-то устройства, автореферат диссертации, гражданский паспорт и др. Математические модели играют огромную роль в научном познании мира с древних лет до настоящего времени. Для описания различных объектов, процессов и явлений в природе и обществе используется математический аппарат — специальный язык математики в виде формул и уравнений. Информационные модели по аналогии с предыдущими двумя типами формируются с помощью языка информатики — цифрового двоичного кода, в который переводятся сведения (данные), представленные в любой форме, в том числе мультимедийной.
Умозрительные модели формируются в аппарате мышления человека на начальной стадии разработки любой модели. Поскольку разные люди по-разному воспринимают одни и те же объекты, процессы, явления, то и умозрительные модели субъективны. Лишь после их формулирования и отделения от сознания автора они становятся знаковыми или материальными.
Итак, моделей в окружающем нас мире такое же множество, как и систем, с которыми мы познакомились в предыдущей главе. А может быть, эти два понятия изоморфны? Как бы то ни было, в познании человеком реального мира оба представления о нем (в виде моделей и систем) используются широко и успешно.
Это понятие тоже неоднозначное. Приведем несколько различных определений, которые позволят нам сформировать об этом некоторое представление.
В Психологическом словаре можно найти следующее:
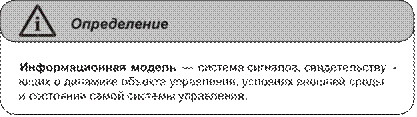
В учебнике «Информатика и математика» (авторы — Р. Р. Яфаева и Н. Ю. Игнатова) дается такое определение:
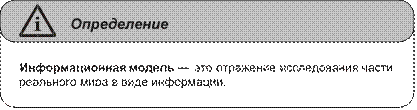
В методических разработках уроков по информатике (Республиканский центр интернет-образования, Республика Беларусь) приводится такое определение:
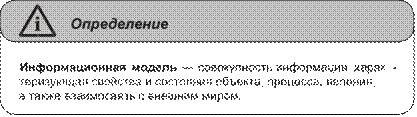
В Википедии (свободной энциклопедии в Интернете, http:// ru.wikipedia.org/wiki/Информационная_модель) приведено синтезированное определение, созданное самими пользователями Интернета:
![]() Информационная модель —
модель объекта, представленная в виде информации, описывающей существенные для
данного рассмотрения параметры и переменные величины объекта, связи между ними,
входы и выходы объекта и позволяющая путем подачи на модель информации об
изменениях входных величин моделировать возможные состояния объекта.
Информационная модель —
модель объекта, представленная в виде информации, описывающей существенные для
данного рассмотрения параметры и переменные величины объекта, связи между ними,
входы и выходы объекта и позволяющая путем подачи на модель информации об
изменениях входных величин моделировать возможные состояния объекта.
Надо отметить, что последнее определение сформировано под влиянием кибернетического подхода к понятиям «модель — система».
Учитывая наше толкование понятия «модель», можно предложить следующую формулировку:
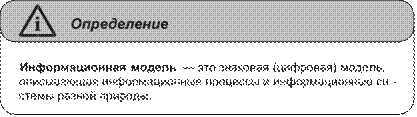
Разработка информационной модели (моделирование) осуществляется в такой последовательности:
1. Определяется цель моделирования.
2. Выбирается тип информационной модели (текстовая, графическая, табличная, математическая).
3. Осуществляется системный анализ объекта моделирования.
4. Проводится построение информационной модели.
5. Тестируется информационная модель по заданным параметрам, отвечающим поставленной цели.
6. В случае необходимости проводится коррекция разрабатываемой информационной модели.
Напомним, что все многообразие моделей можно условно разделить на три класса: материальные, знаковые и умозрительные. Знаковые модели можно поделить еще на три типа: описательные, математические и информационные.
Информационные модели, в свою очередь, составляют огромное множество различных модельных представлений информационных систем, поэтому их классификацию можно осуществить по разным признакам. Одна из них (по иерархическому принципу) представлена на рис. 6.1.
На первом уровне такой древовидной структуры содержатся два типа информационных моделей: модели объектов и процессов и модели знаний. Модели этих типов различаются по технологии моделирования: в первом случае в основу закладывается формирование базы данных, во втором — базы знаний.
База данных — это структурированная совокупность фактов, относящаяся к определенному объекту (процессу). Например, если рассматривать жесткий диск компьютера как объект моделирования, то файловая система компьютера будет представлять собой базу данных.
База знаний — это совокупность основополагающих фактов и правил в определенной предметной области. Факт — это сведения о конкретном событии, о свойстве конкретного объекта, о его связи с другими объектами. Правила — это утверждения, определяющие одни понятия через другие, устанавливающие взаимосвязи между различными свойствами объектов, формулирующие законы природы или общества.
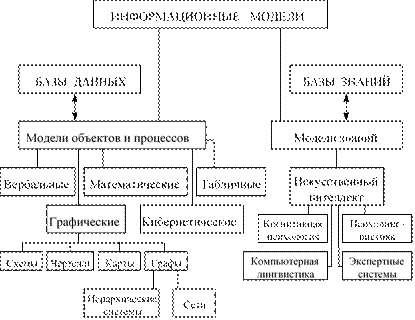
Рис. 6.1. Классификация информационных моделей по иерархическому принципу
На основе фактов формируются знания о предметной области, а правила позволяют интеллектуальной системе самой построить программу для выполнения заданий, поставленных пользователем. В базе знаний могут реализовываться процедуры обобщения и корректировки хранимых знаний, а также процедуры, создающие новые знания на основании тех, которые уже там имеются. Таким образом, знания, хранимые в базе знаний, отличаются от данных, хранящихся в базе данных. Во-первых, структура знаний намного сложнее структуры данных. Во-вторых, знания обладают свойством внутренней активности. Изменения в знаниях могут активизировать те или иные программы, связанные с этими знаниями, а смена данных оставляет базу данных пассивной к происшедшим изменениям.
Модели объектов и процессов можно разбить на пять групп: вербальные, математические, кибернетические, табличные, графические.
Под вербальными моделями понимаются описательные мо дели в цифровом виде, пригодном для обработки на компьютере. В эту группу входят и математические модели, доведенные до стадии алгоритма.
Кибернетические модели — это модели, использующие принцип «черного ящика» (см. главу 5). О внутреннем содержании этого состояния можно судить, подавая сигналы на вход «ящика» и наблюдая его реакцию на выходе из «ящика».
В группу табличных информационных моделей попадают электронные таблицы видов «объект—свойство», «объект—объект» и «двоичная матрица». В каждой строке таблицы «объект— свойство» содержится информация об одном объекте или одном событии. В таблицах «объект—объект» отображаются взаимосвязи между разными объектами. В таблицах «двоичная матрица» отображается качественный характер связи между объектами.
В группе графических информационных моделей выделяют четыре вида моделей: схемы, чертежи, карты, графы. Графы, в свою очередь, разбиты на две категории — иерархические системы и сети. Граф — это информация о составе и структуре системы, представленная в графической форме. Элементы системы называются вершинами, связи между ними — отношениями. Симметричные (двунаправленные) связи называются ребрами, несимметричные (однонаправленные) — дугами. Графы бывают ненаправленными (симметричные связи), ориентированными (несимметричные связи) и неоднородными (разные типы отношений).
Иерархические системы — это системы, элементы которых находятся друг с другом в отношении вложенности, или подчиненности. Дерево — это граф иерархической системы, в котором нет петель. Вершины верхнего уровня связаны с вершинами нижнего уровня как «один ко многим». Сеть — это граф, в котором вершины различных уровней связаны между собой по принципу «многие-ко-многим».
Модели знаний — это модели интеллектуальных информационных систем, объединенных под общим названием «искусственный интеллект».
Искусственный интеллект — раздел информатики, изучающий трудно формализуемые задачи имитации человеческого мышления. Основная цель — стремление проникнуть в тайны творче ской деятельности людей, их способности к овладению знаниями, навыками и умениями. Если будет разгадана суть этой тайны, то есть надежда реализовать подобие творческого начала людей в искусственных системах — сделать эти системы интеллектуальными. В действительности, искусственный интеллект — самостоятельная наука, зародившаяся во второй половине в. на базе вычислительной техники, программирования, математической логики, психологии, лингвистики, нейрофизиологии и других областей знаний. Основной целью этой науки является создание набора так называемых метапроцедур, необходимых и достаточных для того, чтобы ЭВМ могли находить по поставленным задачам их решения.
Метапроцедуры, в отличие от обычных процедур, используемых при решении формализуемых задач, реализуются в интеллектуальной деятельности человека. В психологии мышления можно выделить три основные модели творческой деятельности. Одна из них — лабиринтная модель, с которой связана метапроцедура целенаправленного поиска в «лабиринте» возможностей. Другая модель — это модель ассоциативного мышления. Связанная с ней метапроцедура «по ассоциации» («похожести», «контрастности», «смежности») используется при решении интеллектуальных задач в программах распознавания образов, обучающих программах и др. Третья модель творческой деятельности — это существование внутренних моделей (представлений) проблемных ситуаций. Здесь метапроцедурами являются нахождение представлений (знаний) и рассуждения с целью поиска адекватного ответа для решения проблемной ситуации. В совокупности все перечисленные метапроцедуры образуют арсенал интеллектуальных средств современных систем искусственного интеллекта. Основные проблемы, изучаемые этой наукой:
r представление знаний — разработка методов и приемов для формализации знаний из различных проблемных областей, обобщение и классификация накопленных знаний, использование знаний при решении задач;
r моделирование рассуждений — изучение и формализация различных схем человеческих умозаключений, используемых в процессе решения разнообразных задач;
r диалоговые процедуры общения на естественном языке, обе спечивающие контакт между интеллектуальной системой и пользователем в процессе решения задач;
r планирование целесообразной деятельности — разработка методов построения программ сложной деятельности на основании тех знаний о проблемной области, которые хранятся в интеллектуальной системе;
r обучение интеллектуальных систем в процессе их деятельности, создание комплекса средств для накопления и обобщения умений и навыков, накапливаемых в таких системах.
Работы по искусственному интеллекту ведутся по таким направлениям, как когнитивная психология, психолингвистика, компьютерная лингвистика, экспертные системы, робототехника и др.
Когнитивная психология занимается изучением природы познавательных процессов, обеспечивающих приобретение, сохранение и трансформацию знания. При изучении и моделировании познавательных процессов используются предположения об аналогии между ними и функциональной архитектурой мультипроцессорных систем, обеспечивающих одновременное протекание многих процессов.
Психолингвистика изучает внутренние связи между мышлением и речью. Эта связь проявляется через взаимодействие глубинного универсально-предметного кода (предмета вообще) и поверхностной структуры, образуемой знаками языка в речи (конкретного предмета). Доказано, что имеется принципиальное различие между процессом мысленного проговаривания при чтении текста «про себя» и процессом внутренней речи — мышлением.
Компьютерная лингвистика — наука, родившаяся в 1960-х гг. на стыке вычислительной техники и лингвистики. В настоящее время выделяют 5 основных направлений работы.
1. Анализ текстов на естественном языке — общие принципы построения естественных языков давно интересуют лингвистов всего мира.
2. Синтез текстов на естественном языке — задача, обратная задаче анализа текстов. Проблема также очень актуальна.
3. Понимание текстов — проблема, интересующая не только лингвистов, но и психологов, философов, педагогов и др.
4. «Оживление» текста. Известно, что в памяти человека зрительные образы сопутствуют прочитанным текстам и наоборот, любой мыслительный образ человек легко может описать словами весьма точно. Текст и зрительный образ как бы объединены в нашем сознании. Изучение того, как происходит интеграция текста и картинки и как по одной составляющей представления появляется вторая — одна из важнейших проблем в работах по искусственному интеллекту. Уже имеются образцы картин, воссозданных по заданному тексту.
5. Модели коммуникации. Появление искусственных систем, способных воспринимать и понимать человеческую речь и тексты на естественном языке, создало предпосылки для непосредственного общения человека и компьютера.
Экспертные системы — одно из прикладных направлений искусственного интеллекта. В отличие от других интеллектуальных систем, экспертная система имеет три главные особенности:
r она адаптирована для любого пользователя;
r она позволяет получать не только новые знания, но и профессиональные умения и навыки, связанные с данными знаниями, т. е. не только дает знать что..., но и знать как...;
r она передает не только знания, но и пояснения и разъяснения,
т. е. обладает обучающей функцией.
Робототехника занимается созданием технических систем, которые способны действовать в реальной среде и частично или полностью заменить человека в некоторых сферах его интеллектуальной и производственной деятельности. Такие системы называются роботами. Любой робот представляет собой объединение четырех взаимосвязанных систем: датчиков, системы искусственного интеллекта, системы управления и системы движения.
1. Что такое модель?
2. В чем состоит различие между моделью и системой?
3. На какие классы можно разделить все многообразие моделей?
4. В чем заключается разница между материальными, знаковыми и умозрительными моделями?
5. Что такое информационная модель? Идентичны ли понятия «информационная модель» и «компьютерная модель»?
6. В чем состоит принципиальная разница между базой данных и базой знаний?
7. Перечислите и дайте краткую характеристику разных групп информационных моделей объектов и процессов.
8. Какие виды моделей используются в группе «графические информационные модели»?
9. Что такое граф?
10. Сколько уровней вложенности представлено в классификации информационных моделей? Какой вид графа здесь используется?
11. В чем разница между моделированием объектов (процессов) и знаний?
12. Какие основные проблемы изучаются в разделе информатики «Искусственный интеллект»?
13. Какими проблемами занимаются когнитивная психология и психолингвистика?
14. Какие основные задачи решаются в научном направлении «компьютерная лингвистика»?
15. Какие основные направления прикладных исследований ведутся по проблеме «искусственный интеллект»?
Глава 7
ОснОвы теОрии алГОритмОв
|
Двоичная арифметика 133
|

Слово «алгоритм» (Algorithmi) происходит от имени крупнейшего математика, астронома и географа аль-Хорезми (из города Хорезм), жившего в IX в. В своем труде «Арифметический трактат» он изложил правила арифметических действий над числами в позиционной десятичной системе счисления. Эти правила и назвали алгоритмами, и именно в таком значении слово «алгоритм» вошло в некоторые европейские языки. Позднее любые действия, направленные на решение какой-либо задачи, стали называть алгоритмами, подразумевая не только решение математической задачи, но и разнообразные правила и инструкции: по сборке мебели, по использованию приборов и устройств, проведению химических или физических опытов, по рукоделию, приготовлению блюд и т. д.
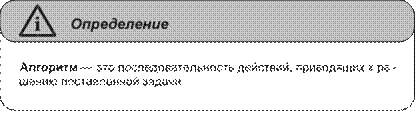
Это самое короткое определение, но есть и другие, которые мы рассмотрим чуть позже, введя необходимые для этого понятия.
Алгоритмизация как процесс конструирования алгоритмов отражает две важные составляющие человеческой деятельности — нормативную и вариативную. В первой закрепляется накопленный в процессе человеческой деятельности опыт, без второй не может быть творчества, развития, движения вперед.

Например, в инструкции по эксплуатации электродвигателя записано «произвести замер сопротивления изоляции с использованием мегомметра». Исполнитель должен понимать смысл этой инструкции, знать, как измерить сопротивление с помощью указанного прибора.

В 20-х гг. прошлого века задача точного определения понятия «алгоритм» стала одной из важнейших проблем математики. Предпринимались многочисленные попытки решить эту задачу, которые привели к возникновению теории алгоритмов, в которую вошли труды многих известных математиков: А. Колмогорова, А. Маркова, А. Тьюринга, Э. Поста и др.
Появление первых проектов вычислительных машин стимулировало развитие этой теории.
![]() Алгоритмы применительно к
вычислительной технике — это точный набор инструкций, описывающих
последовательность действий (шагов) исполнителя для достижения результата,
решения некоторой задачи за конечное время.
Алгоритмы применительно к
вычислительной технике — это точный набор инструкций, описывающих
последовательность действий (шагов) исполнителя для достижения результата,
решения некоторой задачи за конечное время.
Такие алгоритмы должны обладать свойствами, которые бы обеспечивали его автоматическое выполнение, а именно:
r понятность — это свойство, которое означает, что алгоритм для данного исполнителя содержит только те команды, которые входят в систему его команд;
r дискретность (прерывность) означает, что алгоритм должен представлять собой последовательность простых шагов;
r определенность (точность) означает, что каждое правило алгоритма должно быть четким и однозначным;
r результативность (конечность) — благодаря этому свойству алгоритм должен приводить к решению задачи за конечное число шагов;
r массовость (универсальность) означает, что алгоритм должен выполняться для любого набора исходных данных, удовлетворяющих условию задачи; при этом исходные данные могут выбираться из некоторой области, которая называется областью применимости алгоритма.
Способы записи алгоритма:
r словесный;
r графический;
r табличный;
r программный.
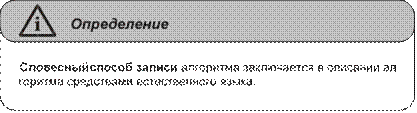
Он применяется при написании инструкций, руководств по эксплуатации, рецептов приготовления и применения лекарств. Например, «1 столовую ложку сушеной ромашки залить стаканом кипятка, дать настояться в течение 15 минут, принимать по 1 столовой ложке 3 раза в день». Недостатки словесного способа:
r словесные описания, как правило, строго не формализуемы;
r они бывают слишком многословны;
r могут допускать неоднозначность толкования (например, «варить до готовности» или «посолить по вкусу» каждый понимает по-своему).
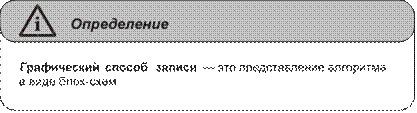
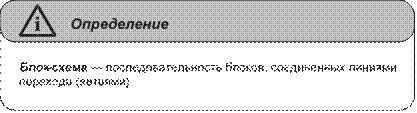
Чтобы не перегружать блок-схему, стрелки на линиях перехода обычно ставятся для указания направления выполнения действий в том случае, если направление противоположно стандартному, а стандартным считается направление сверху вниз и слева направо.
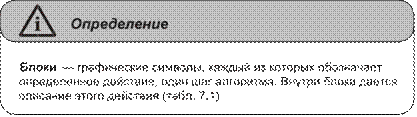
Таблица 7.1. Обозначения основных блоков
|
Название блока |
Вид блока |
Действие |
|
|
Начало, Останов |
|
Начало и конец блоксхемы |
|
|
Данные |
|
Ввод-вывод данных |
|
|
Процесс |
|
Вычислительное действие |
|
|
Решение |
|
Проверка условия |
|
|
Подготовка |
|
Начало цикла |
|
|
Дисплей |
|
Вывод результата на экран |
|
|
Документ |
|
Вывод результата на печать |
Графическое изображение алгоритма используется непосредственно перед этапом записи алгоритма на каком-либо языке программирования из-за его наглядности, т. к. зрительное восприятие обычно облегчает написание программы, предотвращает возможные логические ошибки. Особенно это важно при обучении основам программирования.
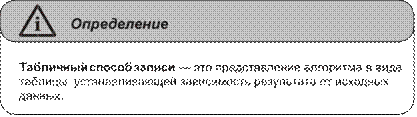
С табличным способом вы знакомились на уроках физики, химии, математики.
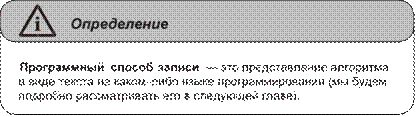
Любой алгоритм может быть представлен в виде комбинации трех базовых (основных) структур:
r следование;
r ветвление;
r цикл.
Поскольку графический способ записи алгоритмов является самым наглядным, мы будем его использовать для представления каждой из этих структур.
Базовая структура «следование» (линейная) показана на рис. 7.1. Такая структура соответствует алгоритму, в котором действия располагаются одно за другим в линейной последовательности.

Рис. 7.1. Следование
Базовая структура «ветвление» содержит не менее одного условия. Если условие справедливо, то выполняется определенное действие.
Приведем варианты этой структуры:
r если — то (рис. 7.2);
r если — то — иначе (рис. 7.3).
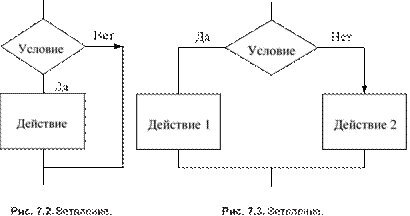
если — то если — то — иначе
Во втором варианте, в отличие от предыдущего, предусмотрено альтернативное действие, которое будет совершаться исполнителем алгоритма в том случае, если условие не выполняется. Есть еще варианты.
r Выбор (рис. 7.4).
Этот вариант иллюстрирует алгоритм, который определяет поведение пешехода у перекрестка. В такой ситуации перебираются три условия: «Свет красный?», «Свет желтый?», «Свет зеленый?». Каждому условию соответствует действие, совершаемое пешеходом при его выполнении. Заметим, что «стоять на месте» в данном случае также считается действием.
r Выбор — иначе (рис. 7.5).
В этом варианте предусмотрено действие, которое будет совершаться исполнителем алгоритма в случае, если ни одно из перечисленных условий не выполняется. Для предыдущего примера это может быть ситуация, когда светофор отключен (ни одно
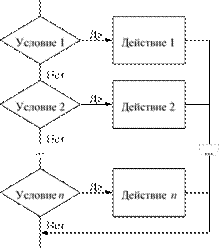
Рис. 7.4. Выбор
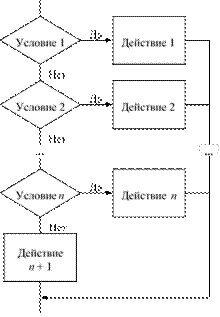
Рис. 7.5. Выбор — иначе
из трех условий не выполняется), и пешеход, не желая переходить нерегулируемый перекресток, может решить перейти улицу в другом месте.
Базовая структура «цикл» содержит повторение одного или нескольких действий. Эти действия называются телом цикла. Существует несколько типов циклов.
r Цикл «для» (рис. 7.6).
В циклах такого типа количество повторений задается с помощью счетчика (переменной цикла). Для этой величины (обозначенной буквой i на рисунке) задаются начальное и конечное значения (например, 1 и 10 соответственно, как показано на рисунке). Каждый раз, как только выполнятся действия, заключенные в теле цикла, значение счетчика увеличивается на значение, которое в списке указано третьим (на рисунке это 1), или, как еще говорят, счетчик «получает приращение». Действия в теле цикла будут снова выполнены при новом значении счетчика, и так будет продолжаться, пока значение счетчика не станет равным указанному конечному значению. Согласно блоксхеме на рисунке действия, заключенные в теле цикла, будут повторяться 10 раз. Величина приращения может быть и отличной от единицы. Например, если она будет равна 2, а не 1, то цикл «прокрутится» только 5 раз, а не 10.
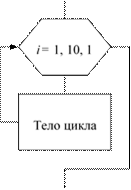
Рис. 7.6. Цикл «для»
r Цикл «пока».
Циклы такого типа используются в том случае, когда заранее неизвестно, сколько раз нужно повторить действия, заключенные в теле цикла, для достижения результата. Например, наполняя водой с помощью стакана какую-нибудь емкость, объем которой не известен, мы не знаем, сколько раз нам придется наполнять стакан и выливать его содержимое в емкость. В циклах такого типа действие (действия) выполняется до тех пор, пока выполняется (рис. 7.7, а) или пока не выполнится (рис. 7.7, б) определенное условие.
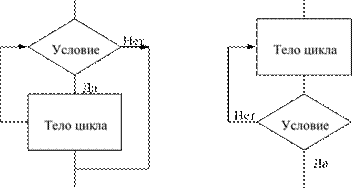
а б
Рис. 7.7. Цикл «пока»: а — с предусловием; б — с постусловием
Первый вариант называется циклом с предусловием (условие проверяется каждый раз до начала выполнения действий, заключенных в теле цикла), второй — циклом с постусловием (в этом варианте условие проверяется после каждого выполнения действий, заключенных в теле цикла).
Реальные алгоритмы обычно являются сочетанием всех основных алгоритмических структур.
З а д а ч а. Есть два сосуда: один — большой, другой — маленький. Необходимо наполнить водой большой сосуд с помощью другого сосуда. Обозначим объем большого сосуда буквой а, маленького сосуда — b. Введем переменную величину, обозначающую объем воды в большом сосуде — x. Пусть в начале выполнения алгоритма x := 0 (в блок-схемах, как и в некоторых языках программирования, операция присваивания значения переменной обозначается «:=»). Словесное описание алгоритма будет следующим.
Шаг 1. Наливаем воду в маленький сосуд b.
Шаг 2. Выливаем из него воду в большой сосуд x := x + b.
Шаг 3. Проверяем, полон ли второй сосуд: x = а? Если — да, то задача решена, если x < а, то снова выполняем шаг 1, и т. д., пока не выполнится условие x = а.
Блок-схема алгоритма будет выглядеть так, как показано на рис. 7.8. Это циклический алгоритм с постусловием.
Научиться «читать» блок-схемы несложно. Для этого нужно знать, какой тип действий обозначает каждый блок, мысленно выполнять действия, переходя от блока к блоку и обращая внимание на стрелки, указывающие направление движения, когда оно противоположно стандартному.
Р а с с м о т р и м з а д а ч у, алгоритм решения которой представлен блок-схемой на рис. 7.9. Нужно определить, какие значения будут иметь а и b после выполнения алгоритма. Требуется также вывести их на экран.
Шаг 1. а := 2, b := 2.
Шаг 2. Проверяем, а = 256? Условие пока не выполняется.
Шаг 3. а := а ^ 2 («^» обозначает возведение в степень, после этого символа указывается показатель степени), b := b + а. Теперь а = 4, b = 6.
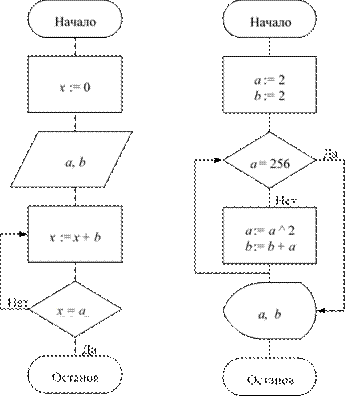
Рис. 7.8. Циклический алгоритм Рис. 7.9. Циклический алгоритм с постусловием с предусловием
Шаг 4. Проверяем, а = 256? Условие пока не выполняется.
Шаг 5. а := 4 ^ 2, т. е. а = 16, тогда b := 6 + 16. Теперь а = 16, b = 22.
Шаг 6. Проверяем, а = 256? Условие пока не выполняется.
Шаг 7. а := 16 ^ 2, т. е. а = 256, тогда b := 256 + 22. Теперь а = 256, b = 278.
Шаг 8. Проверяем, а = 256? Условие выполняется.
Шаг 9. Выводим на экран полученные значения: 256, 278.
Как видим, это циклический алгоритм с предусловием. Величины получали новые значения до тех пор, пока не выполнилось
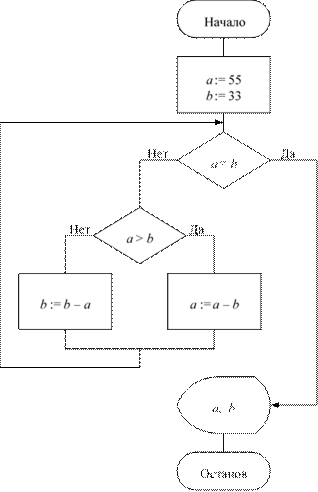
Рис. 7.10. Блок-схема к задаче построения алгоритма по словесному описанию
условие. Как только оно стало справедливым, значения были выведены на экран.
Р а с с м о т р и м з а д а ч у построения блок-схемы алгоритма, который описан словесно.
Значениями переменных а и b являются натуральные числа.
1. Пусть а = 55 и b = 33.
2. Если а = b, то завершаем выполнение алгоритма, иначе переходим к следующему пункту.
3. Если а > b, то а := а – b, иначе b := b – а.
4. Выполняем пункт 2.
Блок-схема будет выглядеть так, как показано на рис. 7.10. После выполнения алгоритма обе переменные будут равны 11.
Для обучения основам формализации задач и построения алгоритмов используют различные вымышленные исполнители (РОБОТ, Черепашка, Кузнечик, Автомат, Калькулятор и т. д.). Для каждого из них определяется система команд. Как правило, одних исполнителей можно отнести к типу «графические» (они могут выполнять движение по траекториям, задаваемым тем или иным алгоритмом, который может содержать ветвления и циклы). Второй тип — «вычислители» (они содержат, как правило, набор команд для выполнения простейших арифметических действий, из которых можно строить алгоритмы вычислений различных величин).
П р и м е р. Система команд исполнителя РОБОТ, «живущего» в клетках квадратного лабиринта на плоскости (рис. 7.11), состоит из команд вверх, вниз, влево, вправо. При выполнении любой из этих команд РОБОТ перемещается на одну клетку, соответственно: вверх ↑, вниз ↓, влево ←, вправо →.
Четыре условия позволяют проверить отсутствие преград у каждой из сторон той клетки, где находится РОБОТ:
|
сверху свободно |
снизу свободно |
слева свободно |
справа свободно |
В цикле пока <условие> команда выполняется, пока условие истинно, иначе происходит переход на следующую строку программы. Если РОБОТ начнет движение в сторону стены, то он разрушится, и выполнение программы прервется.
Требуется определить: сколько клеток лабиринта соответствует требованию, что, выполнив предложенную программу, РОБОТ уцелеет и остановится в той же клетке, с которой он начал движение?
НАЧАЛО
ПОКА <справа свободно> вниз
ПОКА <снизу свободно> влево
ПОКА <слева свободно> вверх
ПОКА <сверху свободно> вправо
КОНЕЦ
Рис. 7.11. Лабиринт
Для удобства разметим лабиринт подобно тому, как размечается шахматная доска (рис. 7.12), чтобы у каждой клетки был адрес (буква столбца и номер строки, на пересечении которых она находится). Обозначим движение в сторону стены, при котором может произойти разрушение РОБОТА, словом STOP.
Можно принимать за стартовую поочередно каждую клетку и выполнять алгоритм (стартовая клетка далее выделена полужирным шрифтом). Начнем с A1.
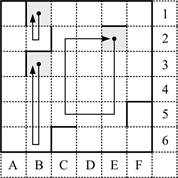
Рис. 7.12. Лабиринт с разметкой
A1 → STOP (т. к. первое условие <справа свободно> не выполняется, и двигаться вниз РОБОТ не будет). Следующее условие <снизу свободно> выполняется. РОБОТ делает шаг на клетку влево и упирается в стену, т. е. гибнет.
A2 → A3 → STOP (т. к. первое условие <справа свободно> выполняется, и РОБОТ делает шаг на клетку вниз, условие <снизу свободно> выполняется, и РОБОТ делает шаг на клетку влево и упирается в стену).
A3 → STOP (т. к. первое условие <справа свободно> не выполняется, второе условие <снизу свободно> выполняется, и РОБОТ делает шаг на клетку влево и упирается в стену).
A4 → A5 → A6 → STOP (т. к. первое условие <справа свободно> выполняется, и РОБОТ делает шаг на клетку вниз, условие <справа свободно> снова выполняется и РОБОТ делает еще шаг на клетку вниз, условие <справа свободно> выполняется, и РОБОТ делает еще шаг на клетку вниз и упирается в стену).
A5 → A6 → STOP (т. к. первое условие <справа свободно> выполняется, и РОБОТ делает шаг на клетку вниз и упирается в стену).
B1 → B2 → B1 (т. к. первое условие <справа свободно> выполняется, и РОБОТ делает шаг на клетку вниз, условие <справа свободно> не выполняется, условие <снизу свободно> не выполняется, условие <слева свободно> выполняется, и РОБОТ делает шаг на клетку вверх и возвращается на стартовую клетку) — первая стартовая клетка, удовлетворяющая условию, найдена.
Таким же образом стартуем из оставшихся клеток и проверяем, сможет ли РОБОТ в них вернуться, выполнив программу.
В результате проверки только три клетки лабиринта (на рисунке выделены серым цветом), могут стать стартовыми для того, чтобы РОБОТ, выполняя данный алгоритм, вернулся в исходную клетку. В остальных случаях РОБОТ на том или ином шаге будет натыкаться на стену.
Решение получается не слишком кратким, но надежным. Существуют, конечно, и другие способы решения подобных задач.
Р а с с м о т р и м е щ е о д н у з а д а ч у. У исполнителя
Калькулятор две команды, которым присвоены номера:
1. прибавь 1
2. умножь на 3
Выполняя первую из них, Калькулятор прибавляет к числу на экране 1, а выполняя вторую, утраивает его. Запишите порядок команд в программе получения 26 из 2, содержащей не более 6 команд, указывая лишь номера команд. Для этого случая можно предложить следующую программу 211211, содержащую 6 команд:
умножь на 3 (2 × 3 = 6) прибавь 1 (6 + 1 = 7) прибавь 1 (7 + 1 = 8) умножь на 3 (8 × 3 = 24) прибавь 1 (24 + 1 = 25) прибавь 1 (25 + 1 = 26)
Р а с с м о т р и м е щ е о д и н а л г о р и т м д л я и с -
п о л н и т е л я. Автомат получает на вход два трехзначных числа. По этим числам строится новое число согласно следующим правилам:
1. Вычисляются три числа — сумма старших разрядов заданных трехзначных чисел, сумма средних разрядов этих чисел, сумма младших разрядов.
2. Полученные три числа записываются друг за другом в порядке убывания (без разделителей).
П р и м е р. Исходные трехзначные числа — 795 и 196, поразрядные суммы: 8, 18 и 11, результат —18118.
Нужно определить, какое из следующих чисел может быть результатом работы автомата:
1) 151004;
2) 161410;
3) 191615; 4) 121613.
Очевидно, что 1-й вариант не подходит, т. к. в записи есть разделитель (0) между предпоследним и последним числом; 3-й вариант тоже не подходит, т. к. максимальное значение разрядной суммы двух старших разрядов заданных трехзначных чисел не может быть больше 18; 4-й вариант не может быть решением задачи, т. к. не соблюдается порядок убывания. Таким образом, подходящим является только 2-й вариант.
В следующей главе, рассматривая особенности записи алгоритмов на языке программирования, мы вернемся к представлению алгоритмов с помощью блок-схем и увидим, как такое представление помогает при изучении основ программирования и написании несложных компьютерных программ.
1. Что такое алгоритм?
2. Каково происхождение этого понятия?
3. Кто может быть исполнителем алгоритма?
4. Что понимают под системой команд исполнителя?
5. В чем заключается формализация задачи?
6. Каковы свойства алгоритма?
7. Какие существуют способы записи алгоритма?
8. Каковы недостатки словесного способа?
9. Каковы преимущества графического способа записи алгоритма по сравнению с другими способами?
10. Какой алгоритм называют линейным?
11. Что является основным признаком разветвленного алгоритма? Приведите примеры различных вариантов базовой алгоритмической структуры «ветвление».
12. Что такое цикл?
13. Что такое счетчик цикла и для чего он нужен?
14. Какие виды циклов вам известны?
15. В виде каких основных алгоритмических структур или их комбинаций можно представить любой алгоритм?
16. Каким будет значение переменной x после выполнения алгоритма, изображенного с помощью блок-схемы на рис. 7.13?
17. Каким будет значение величины c после выполнения алгоритма, изображенного с помощью блок-схемы (рис. 7.14)?
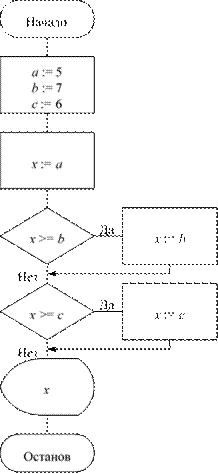
Рис. 7.13. Блок-схема к заданию 16
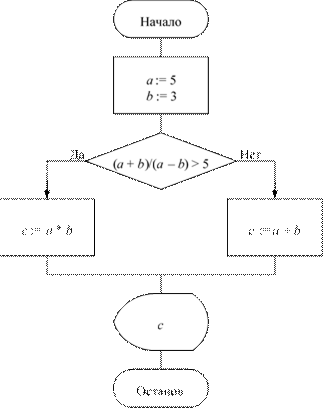
Рис. 7.14. Блок-схема к заданию 17
18. Сколько клеток лабиринта (см. рис. 7.11) соответствуют требованию, что, выполнив предложенную программу, РОБОТ уцелеет и остановится в той же клетке, с которой он начал движение?
НАЧАЛО
ПОКА <слева свободно> вправо
ПОКА <справа свободно> влево
ПОКА <снизу свободно> вниз
ПОКА <сверху свободно> вверх
КОНЕЦ
19. У исполнителя Калькулятор две команды, которым присвоены номера:
1. прибавь 2
2. умножь на 3
Первая из них увеличивает число на экране на 2, вторая — утраивает его. Программа для Калькулятора — это последовательность команд. Запишите порядок команд в программе получения числа 41 из числа 3, содержащей не более 5 команд, указывая лишь номера команд. (Например, 21211 — это программа умножь на 3 прибавь 2 умножь на 3 прибавь 2 прибавь 2 которая преобразует число 2 в 28.)
20. Автомат получает на вход два трехзначных числа. По этим числам строится новое число согласно следующим правилам.
1. Вычисляются три числа — сумма старших разрядов заданных трехзначных чисел, сумма средних разрядов этих чисел, сумма младших разрядов.
2. Полученные три числа записываются друг за другом в порядке возрастания (без разделителей).
П р и м е р. Исходные трехзначные числа: 621, 772.
Поразрядные суммы: 15, 9, 3. Результат: 3915.
Нужно определить, какое из следующих чисел может быть результатом работы автомата:
1) 131110;
2) 161821;
3) 111315;4) 70912.
Задание 16
Р е ш е н и е.
Для определения значения переменной x после выполнения алгоритма, изображенного с помощью блок-схемы (см. рис. 7.13), выполним действия:
Шаг 1. а := 5, b := 7, с := 6.
Шаг 2. x := a, т. е. x := 5.
Шаг 3. Проверяем, x >= b, т. е. 5 >= 7? Условие не выполняется.
Шаг 4. Проверяем, x >= c, т. е. 5 >= 6? Условие не выполняется.
Шаг 5. Выводим на экран x, т. е. 5.
Ответ: x = 5.
Задание 17
Р е ш е н и е.
Для определения значения переменной с после выполнения алгоритма, изображенного с помощью блок-схемы (см. рис. 7.14), выполним действия:
Шаг 1. а := 5, b := 3.
Шаг 2. Проверяем, (а + b)/(a – b) > 5, т. е. (5 + 3)/(5 – 3) > 5?
Условие не выполняется.
Шаг 3. c := a + b, т. е. c := 5 + 3.
Шаг 4. Выводим на экран значение величины c, т. е. 8.
Ответ: c = 8.
Задание 18
Р е ш е н и е.
Принимая поочередно каждую клетку за стартовую, выполним алгоритм (рис. 7.15).
A1 → A2 → A3 → A4 → A5 → A6 → A5 → A4 → A3 → A2 → A1 (т. к. первое условие <слева свободно> не выполняется, второе условие <справа свободно> не выполняется, третье условие <снизу свободно> выполняется, и РОБОТ передвигается по клеткам вниз до тех пор, пока не достигнет клетки A6, в ней условие <снизу свободно> не выполняется, но следующее условие <сверху свободно> выполняется, и РОБОТ клетка за клеткой будет двигаться вверх, пока не вернется на стартовую клетку).
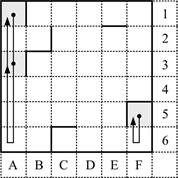
Рис. 7.15. К решению задания 18
A2 → STOP (т. к. первое условие <слева свободно> не выполняется, условие <справа свободно> выполняется, и РОБОТ упирается в стену).
A3 → A4 → A5 → A6 → A5 → A4 → A3 (т. к. первое условие <слева свободно> не выполняется, условие <справа свободно> не выполняется, условие <снизу свободно> выполняется, и РОБОТ передвигается по клеткам вниз до тех пор, пока не достигнет клетки A6, в ней условие <снизу свободно> не выполняется, но следующее условие <сверху свободно> выполняется, и РОБОТ клетка за клеткой будет двигаться вверх, пока не вернется на стартовую клетку).
A4 → STOP (т. к. первое условие <слева свободно> не выполняется, условие <справа свободно> выполняется, и РОБОТ упирается в стену).
A5 → STOP (т. к. первое условие <слева свободно> не выполняется, условие <справа свободно> выполняется, и РОБОТ упирается в стену).
A6 → STOP (т. к. первое условие <слева свободно> не выполняется, условие <справа свободно> выполняется, и РОБОТ упирается в стену).
И т. д.
Можно представить результат выполнения алгоритма при старте из каждой клетки в виде таблицы.
|
A1 → A2 → A3 → A4 → A5 → A6 → A5 → A4→ A3 → A2→ A1 |
B1 → STOP |
С1 → D1→ E1 → F4→ STOP |
D1 → E1 → F4 → STOP |
E1 → F1 → STOP |
F1→ STOP |
|
A2 → STOP |
B2 → STOP |
С2 → STOP |
D2 → E2 → F2 → STOP |
E2 → F2 → STOP |
F2→ STOP |
|
A3 → A4 → A5 → A6→ A5 → A4 → A3 |
B3 → STOP |
С3 → D3 → E3 → F3 → STOP |
D3 → E3 → F3 → STOP |
E3 → F3 → STOP |
F3 → STOP |
|
A4 → STOP |
B4 → С4 → D4 → E4 → F4 → STOP |
С4 → D4 → E4 → F4 → STOP |
D4 → E4 → F4 → STOP |
E4 → F4 → STOP |
F4→ STOP |
|
A5 → STOP |
B5 → С5 → D5 → E5 → STOP |
С5→ D5→E5→ STOP |
D5→E5→ STOP |
E5→ STOP |
F5→ F6→ F5 |
|
A6 → STOP |
B6 → STOP |
C6→ STOP |
D6 → E6 → F6 → STOP |
E6 → F6 → STOP |
F6→ STOP |
Как видим, заполнить таблицу гораздо проще, чем кажется на первый взгляд, т. к. в большинстве случаев РОБОТ натыкается на границу уже на 1-м, 2-м или 3-м шаге.
Ответ: 3 клетки (выделены на рис. 7.15 и в таблице — цветом).
Задание 19
Р е ш е н и е.
Программа получения числа 41 из числа 3 — это 21121, она содержит 5 команд:
умножь на 3 (3 × 3 = 9) прибавь 2 (9 + 2 = 11) прибавь 2 (11 + 2 = 13) умножь на 3 (13 × 3 = 39) прибавь 2 (39 + 2 = 41) Ответ: 21121.
Задание 20
Р е ш е н и е.
Очевидно, что 1-й вариант не подходит, т. к. не соблюдается порядок возрастания, 2-й вариант тоже не подходит, т. к. максимальное значение разрядной суммы не может быть больше 18; 4-й вариант не может быть решением задачи, т. к. в записи есть разделитель (0). Таким образом, подходящим является только 3-й вариант.
Ответ: 3-й вариант.
|
Двоичная арифметика 163
|
Глава 8
Программный сПособ заПиси алгоритмов

В предыдущей главе рассматривались различные способы записи алгоритмов. Для того чтобы алгоритм мог быть выполнен компьютером, необходимо записать его на одном из языков программирования. Языком программирования ЭВМ первого поколения был язык машинных кодов (язык низкого уровня). Затем появились языки-ассемблеры. В них числовые коды команд для удобства заменили мнемокодами — их буквенными обозначениями (см. главу 2).
В ЭВМ второго поколения стали использоваться языки высокого уровня. Команды языка высокого уровня (операторы) — это слова естественного языка (английского, например), что упрощает работу программиста. Каждый оператор имеет соответствующий формат (определяющий правила записи оператора).
Например, почти во всех языках программирования есть оператор if...then...[else], который позволяет записать разветвленный алгоритм (в квадратные скобки заключается обычно необязательная часть оператора). Формат этого оператора: if (условие) then (действие) else (действие)
В процессе выполнения программы, если условие справедливо, будет выполнено то действие, которое указано после слова then, а если не справедливо то действие, которое указано после else.
Языков программирования довольно много, к распространенным языкам относятся такие, как BASIC, Pascal, С, C++.
Чтобы компьютер мог выполнить программу, написанную на каком-либо языке программирования, необходимо, чтобы на компьютере была установлена соответствующая среда программирования. Существуют также интегрированные среды, в которых есть возможность выбирать язык для записи алгоритма, например RAD Studio 2009. Эта среда сочетает в себе две среды: Delphi (в ее основе — язык Pascal) и C++Builder (в основе которой — C++).
Среда программирования (среда разработки приложений) обычно включает редактор (для написания и редактирования программы) и транслятор («переводчик»).
![]() Программы
на языке Машинные
Программы
на языке Машинные
Транслятор
высокого уровня коды
Рис. 8.1. Схема работы транслятора
Трансляторы, выполняющие перевод программы, написанной на языке программирования, в машинные коды (рис. 8.1), бывают двух типов — интерпретаторы или компиляторы.
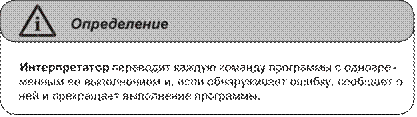
Программный способ записи алгоритмов
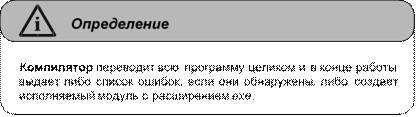
Исполняемый модуль можно запускать на любом компьютере, даже не имеющем в своем программном обеспечении среды, в которой он был создан.
Объектно-ориентированная среда программирования предоставляет в распоряжение программиста не только редактор и транслятор, но и готовые объекты — в основном элементы интерфейса операционной системы Windows или другой графической среды.
Одним из самых популярных языков программирования является Pascal. Разработанный в 1967 г. профессором Никлаусом Виртом, этот язык быстро превратился из средства обучения студентов программированию в инструмент для создания новых программных проектов. Язык назван в честь Блеза Паскаля (1623–1662), внесшего большой вклад в историю развития средств вычислительной техники, поразившего современников своим изобретением — механической машиной, с помощью которой можно было выполнять над числами четыре арифметических действия, и которую он постоянно совершенствовал.
Существуют различные среды программирования: Turbo Pascal и Borland Pascal для операционной системы DOS, Lazarus для OC Linux, Delphi для OC Windows, в основе которых лежат разные версии языка Pascal (Object Pascal, Free Pascal и т. д.). Одно из достоинств языка — лаконичность. Он был создан в то время, когда языков высокого уровня было немного, к тому же все они, в отличие от языка Pascal, были созданы для решения узкоспециальных задач (инженерных, экономических и т. д.). Основные элементы языка Pascal:
r алфавит языка (совокупность используемых символов: латинские буквы, арабские цифры, специальные символы);
r переменные величины;
r постоянные величины (константы);
r выражения;
r функции;
r массивы;
r операторы; r служебные слова; r знаки операций.
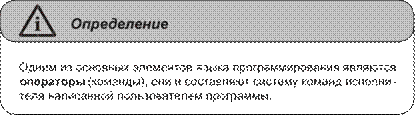
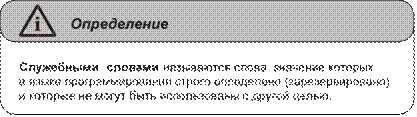
Служебные слова применяются, например, для обозначения операторов, описаний типов данных, некоторых операций.
Все величины имеют имена (идентификаторы), которые присваиваются величинам по определенным правилам:
r имя может состоять из буквы или последовательности букв латинского алфавита, цифр и символа подчеркивания, но первой в такой последовательности должна быть обязательно буква или символ подчеркивания;
r имя не должно совпадать с зарезервированными словами;r желательно, чтобы имя отражало смысл величины.
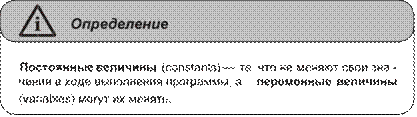
Среди величин (и постоянных, и переменных) можно выделить типы, представленные на рис. 8.2. Все типы величин описаны в справочной системе среды программирования.
Текст любой программы начинается словом program, за которым следует имя программы и объявления (описания типа) величин, которые в ней используются. Это необходимо, поскольку данные разных типов обрабатываются в соответствии с разными правилами. Описание типов постоянных величин дается в программе после служебного слова const (от англ. constants — постоянные). Описание типов переменных — после служебного слова var (от англ. variables — переменные). Справочная система всегда поможет выяснить, как следует описывать величину того или иного типа.
Например, описание переменной величины целого типа (nteger), имеющей имя I, выглядит так:
var
I: Integer;
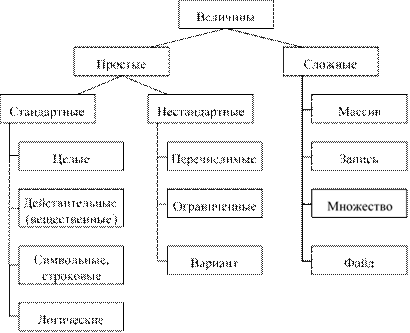
Рис. 8.2. Типы величин
Значения переменных типа Real, включая Single, Double (соответствующих одинарной и двойной точности), могут записываться в обычной (например, 0.752) или экспоненциальной форме (7.52E-1, т. е. 7.52 × 10–1). Разделителем между целой и дробной частями служит точка, а не запятая! Объявление переменной величины вещественного типа Real выглядит так:
var
I: Real;
Величины типа Boolean (булевы, или логические) могут принимать только одно из двух значений — False (Ложь) или True (Истина), и объявляется такая величина следующим образом:
var
I: Boolean;
Значением величины типа Char (символьные) может быть один символ, например буква. Объявление величины записывается так:
var
I: Char;
Значением величины типа String (строковые) может быть строка символов (длина строки — до 255 символов). Объявляется она аналогично:
var
I: String;
Все указанные типы величин, как показано на рис. 8.2, относятся к простым стандартным величинам.
К сложным типам относится, прежде всего, Array (массив). Он позволяет связать с одним именем совокупность однотипных данных.

В одномерном массиве порядковый номер (индекс) элемента в массиве указывается в квадратных скобках после имени. Объявлять массивы можно, например, так:
Var MyArray : Array [1..100] of Char;
В примере объявлен одномерный массив с именем MyArray, который является последовательностью 100 элементов символь- ного типа.
В двумерном массиве для каждого элемента массива в квадратных скобках после имени пишут пару индексов, указывающих номер строки и номер столбца — координаты элемента в таблице. Есть разные способы объявления двумерного массива. Например, двумерный массив Matrix вещественного типа, размерностью 10 × 50 можно объявить двумя способами:
Type TMatrix = array [1..10] of array [1..50] of Real; или
Type TMatrix = array [1..10, 1..50] of Real; Можно воспользоваться любым из них.
![]() Выражением в Object Pascal называют
комбинацию идентификаторов (имен величин), стандартных функций, чисел, знаков
операций и др. Операции (сгруппированные по типам) и их обозначения в языке
Object Pascal представлены в табл. 8.1.
Выражением в Object Pascal называют
комбинацию идентификаторов (имен величин), стандартных функций, чисел, знаков
операций и др. Операции (сгруппированные по типам) и их обозначения в языке
Object Pascal представлены в табл. 8.1.
Таблица 8.1. Операции в Object Pascal
|
Арифме- тические операции |
Действие |
Логи- ческие операции |
Действие |
Опера- ции отно- шения |
Действие |
|
+ |
Сложение |
not |
Логическое отрицание |
= |
Равно |
|
- |
Вычитание |
and |
Логическое И |
<> |
Не равно |
|
* |
Умножение |
or |
Логи- ческое ИЛИ |
> |
Больше |
|
/ |
Деление |
xor |
Исклю- чающее ИЛИ |
< |
Меньше |
|
Div |
Целочисленное деление (деление с округлением частного) |
|
|
<= |
Меньше или равно |
|
Mod |
Остаток от деления двух чисел |
|
|
>= |
Больше или равно |
При решении задач и записи их на языке Oect Pascal можно также использовать стандартные функции. Они представлены в табл. 8.2 (математические) и 8.3 (некоторые другие стандартные функции). Для стандартных математических функций тип аргументов Integer или Real, тип результата — Real. Только для функции abs() тип результата может быть Integer при типе аргумента Integer.
Таблица 8.2. Стандартные математические функции в Object Pascal
|
Имя функции |
Математическое соответствие |
Имя функции |
Математическое соответствие |
|
sin(x) |
sin x |
sqr(x) |
x2 |
|
cos(x) |
cos x |
sqrt(x) |
|
|
ln(x) |
ln x |
arctan(x) |
arctg x |
|
exp(x) |
ex |
abs(x) |
|x| |
Таблица 8.3. Стандартные функции в Object Pascal
|
Имя функции |
Тип аргумента |
Результат |
|
oDD(x) |
Real, Integer |
Для четного х — False, для нечетного x — True |
|
SuCC(x) |
Real, Integer |
Следующее по порядку значение. Для целых выражений эквивалентно x + 1 |
|
pReD(x) |
Real, Integer |
Предыдущее по порядку значение. Для целых выражений эквивалентно x – 1 |
|
TRunC(x), InT(x) |
Real |
Целая часть х (дробная отбрасывается) |
|
RounD(x) |
Real |
Округление до ближайшего целого |
|
oRD(S) |
Char |
Порядковый номер символа S в символьной строке |
|
ChR(I) |
Integer |
Символ, стоящий под номером I в символьной строке |
|
ChR(oRD(S))=S |
|
Соотношение между функциями oRD() и ChR() |
Чтобы записать на языке программирования один из простейших алгоритмов (например, вычисление неизвестной величины через известные величины, введенные с клавиатуры), необходимо использовать несколько операторов: присваивания (для выполнения вычислений), ввода известных величин, вывода результата.
Чтобы воспользоваться оператором, нужно знать его формат.
![]() Формат оператора определяет
правила его записи, показывает, какие величины и в какой последовательности нужно
указать, какие между ними следует ставить знакиразделители, есть ли
необязательная часть записи оператора, а если есть, то какая именно
(необязательная часть заключается в квадратные скобки).
Формат оператора определяет
правила его записи, показывает, какие величины и в какой последовательности нужно
указать, какие между ними следует ставить знакиразделители, есть ли
необязательная часть записи оператора, а если есть, то какая именно
(необязательная часть заключается в квадратные скобки).
r := — оператор присваивания.
Формат: имя_переменной:=ее_значение;
Этот оператор присваивает величине какого-либо типа то или иное значение, соответствующее типу величины. Например:
a:=0.
r read — оператор ввода.
Формат: read(имя_переменной, ...);
Например: read(x, y).
r readln — оператор ввода, который переводит курсор на следующую строку (если аргументов нет, то он переводит программу
в режим ожидания ввода, и окно приложения не закроется, пока не будет нажата любая клавиша).
Формат: readln;
r write — оператор вывода.
Формат: write('текст', имя_переменной, ...);
Например: write('z= ',z).
r writeln — оператор вывода, который переводит курсор на следующую строку.
Следует помнить, что операторы языка Pascal разделяются точкой с запятой.
Операторы бывают простые и составные (заключенные в операторные скобки begin ... end). О составных операторах речь пойдет в следующем разделе.
Комментарий к строкам программы заключается в фигурные скобки { } и помогает читать программу, облегчая понимание алгоритма.
П р и м е р. Пусть сотрудник предприятия получает 500 руб. 75 коп. в день. Нужно определить, какую заработную плату ему начислят за 24 рабочих дня с учетом надбавки (коэффициента в размере 2.49).
Алгоритм вычисления можно записать в виде программы (см. листинг 8.1).
![]()
program Demo1; const Cnt=2.49; var pay: Real;
Total: Real;
begin pay:=500.76; {получает сотрудник предприятия в день} Total:=pay*24*Cnt; {получает сотрудник за 24 дня с учетом коэффициента}
Writeln('Result = ', Total);
Readln; {чтобы не закрылось окно до нажатия клавиши enter} end.
Условные операторы.
Простые и составные условия.
В главе 7 мы уже отмечали, что любой алгоритм может быть представлен в виде комбинации трех базовых (основных) структур: следование, ветвление и цикл.
Базовая структура «следование» (линейная) соответствует алгоритму, в котором одно действие следует за другим в линейной последовательности (как в программе, представленной листингом 8.1).
Базовая структура «ветвление» содержит не менее одного условия. Если условие справедливо, то выполняется определенное действие. Чтобы записать на языке программирования разветвленный алгоритм (т. е. алгоритм, содержащий одно или более условий), необходимо использовать условные операторы. К таким операторам относится оператор if ...then...[else].
Его формат: if условие then оператор_1 [else оператор_2];
Условие может быть простым, в котором величины связаны операциями сравнения (например, a>10, c<b), или составным, состоящим из простых условий, связанных логическими операциями (например, (c<a) and (c<b), в этом случае каждое из простых условий берется в скобки).
Если условие справедливо, то выполняется оператор_1, в противном случае будет выполняться оператор_2. Этими операторами могут быть любые операторы, в том числе и условный оператор.
П р и м е р. Пусть нужно найти наибольшее из трех чисел a, b, c. Алгоритм решения этой задачи можно описать словесно. Если a>b и одновременно a>c, то наибольшим числом является а. Если эти условия не выполняются и к тому же b>c, то наибольшим числом будет b. Иначе наибольшим числом будет с. Этот алгоритм можно представить в виде блок-схемы (рис. 8.3), а программу можно записать так, как показано в листинге 8.2.
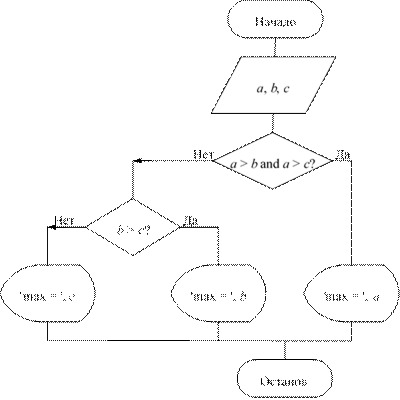
Рис. 8.3. Блоксхема алгоритма поиска наибольшего из трех чисел
![]()
program Demo2; var
a, b, c: integer; begin
Write('Введите три числа '); Readln(a, b, c); if (a>b) and (a>c) then
Write(' max = ', a) else if (b>c) then
Write(' max = ', b) else
Write(' max = ', c); Readln; end.
case...of — условный оператор, который еще называют оператором выбора, выполняет сравнение значения переменной величины с заранее определенным множеством случаев, заданных соответствующими значениями. Он реализует такой вариант базовой алгоритмической структуры ветвление, как выбор.
Его формат:
case имя_переменной of значение_1: оператор_1; значение_2: оператор_2; ... значение_n: оператор_n; end;
П р и м е р. Необходимо составить программу ввода ответа в виде одной буквы с последующей его интерпретацией: если введена буква «Д», то считать ответ положительным, если буква «Н» — отрицательным, а если введена любая другая буква, должно быть выведено сообщение «ответ непонятен».
Программа приведена в листинге 8.3.
![]()
program Demo3; var userIn: Char; begin
Writeln('Введите Д (при положительном ответе) или Н (при отрицательном ответе)'); Read(userIn); case userIn of
'Д': Writeln('Вы ответили "да"'); 'Н': Writeln('Вы ответили "нет"'); else Writeln('ответ непонятен'); end; end.
Чтобы записать на языке программирования циклический алгоритм (с многократным повторением одного или нескольких действий), необходимы операторы цикла. Один из них — оператор For ... do. Он используется тогда, когда известно количество повторений.
Его формат:
For i:=начальное_значение to конечное_значение do begin оператор(ы); end;
Здесь i — это переменная цикла, называемая также параметром цикла, или счетчиком, операторы после do (между begin и end) называются телом цикла.
Операторы, составляющие тело цикла, выполняются столько раз, сколько укладывается между начальным и конечным значениями переменной цикла. При каждом прохождении цикла (выполнении операторов в теле цикла) переменная цикла по умолчанию увеличивается на единицу (получает приращение). Это приращение (шаг) может быть как положительным, так и отрицательным (в этом случае начальное значение должно быть больше конечного, а вместо to пишется downto).
П р и м е р. Пусть нужно определить количество страниц, напечатанных автором за определенное количество дней, если предусмотрен ввод количества страниц, отпечатанных в течение каждого дня.
Программа приведена в листинге 8.4.
![]()
program Demo4; var
Count: Integer; number: Integer; I: Integer; Result: Integer; begin
{вычисление количества страниц, которые автор написал за определенное количество дней}
Write('Сколько дней работал автор?');
Readln(Count);
Result:=0;
For I:=1 to Count do begin
Write('Сколько страниц за ', I, 'день?');
Readln(number);
Result:= Result+number; {рекуррентное суммирование} end;
Writeln('Результат - ', Result); Readln; end.
После запуска программы нужно ввести число (количество дней). Это значение будет присвоено переменной Count. Количество страниц, обозначенное переменной Result, сначала обнуляется (или, как еще говорят, инициализируется).
Пусть было введено число 5, тогда все действия в теле цикла будут выполнены 5 раз. При выполнении этих действий (при первом проходе цикла) на экран будет выведено сообщение «Сколько страниц за 1 день?», после этого введенное с клавиатуры количество страниц присваивается переменной number, которое прибавляется к значению Result.
При втором проходе цикла на экран будет выведено сообщение «Сколько страниц за 2 день?», вводится новое значение количества страниц и присваивается переменной number. А это значение, в свою очередь, прибавляется к значению Result.
Таким образом, при каждом проходе цикла к значению переменной Result будет добавляться количество страниц, напечатанное за очередной день. После последнего прохода цикла получим окончательное значение — количество страниц, напечатанных за 5 дней. Такой метод определения суммы последовательности чисел получил название рекуррентное суммирование.
![]() Формулы, в которых очередной член последовательности выражается
через один или несколько предыдущих членов, называются рекуррентными соотношениями.
Метод, использующий рекуррентные соотношения, называется рекуррентным.
Формулы, в которых очередной член последовательности выражается
через один или несколько предыдущих членов, называются рекуррентными соотношениями.
Метод, использующий рекуррентные соотношения, называется рекуррентным.
В программировании часто используют метод рекуррентного суммирования для определения суммы конечной последовательности чисел. Применив рекуррентный метод, получим соотношения:
S0 = 0
Sk = Sk−1 + xk, k = 1, 2, ..., n
S = Sn
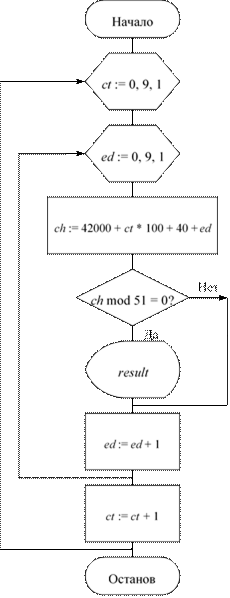
Рис. 8.4. Блоксхема алгоритма восстановления возможных значений числа
Сумма здесь представлена в виде переменной величины, которая увеличивается, как только к ней прибавляется очередной элемент последовательности, на величину этого элемента. Процесс напоминает нанизывание бусинок на нить. Итогом процесса будет сумма элементов последовательности. Пример рекуррентных соотношений — формулы определения членов арифметических и геометрических прогрессий.
Если тело цикла содержит другой цикл, то такие циклы называются вложенными. При выполнении программы, в которой есть вложенные циклы, внутренний цикл полностью «прокручивается» для каждого значения переменной внешнего цикла. Например, если максимальное значение переменной внешнего цикла равняется 5, а внутреннего — 4, то действия, составляющие тело внутреннего цикла, будут повторяться 20 раз.
В листинге 8.5 представлен текст программы, а на рис. 8.4 дана соответствующая блок-схема алгоритма восстановления возможных значений числа, в котором пропущены цифры в двух разрядах. По условию задачи эти числа должны быть кратны 51, т. е. остаток от деления числа на 51 (его можно определить с помощью операции mod) должен быть равен нулю. Для выполнения перебора и подстановки цифр используются вложенные циклы.
![]()
program Demo5;
{Восстановление вариантов чисел 42*4* при условии, что они кратны 51} var
ch, ct, ed: integer; begin for ct:=0 to 9 do for ed:=0 to 9 do begin
ch:=42000+ct*100+40+ed; if (ch mod 51)=0 then Writeln(ch, ' - кратно 51'); end; Readln; end.
Если заранее не известно количество повторений цикла, то можно повторять действия, пока выполняется определенное условие.
Условие может проверяться до начала выполнения операторов, входящих в тело цикла (цикл с предусловием) или после их выполнения (цикл с постусловием).
Repeat ... until — оператор цикла с постусловием (операторы между repeat и until будут повторяться, пока не выполнится условие, определенное логическим выражением, указанным после ключевого слова until).
Его формат: repeat оператор(ы); until логическое_выражение;
В листинге 8.6 представлен текст программы, в которой используется данный оператор для построения алгоритма угадывания числа, «задуманного» генератором случайных чисел (специальной функции random(r)):
![]()
program Demo6; var
mynumb, yournumb: integer; const r=7; begin randomize;
Writeln('Угадай задуманное число ');
mynumb:=random(r)*20; {"задуманное" число задается через генератор случайных чисел} repeat begin
Read(yournumb); {угадывание задуманного числа} if yournumb>mynumb then Writeln('слишком большое') else if yournumb<mynumb then Writeln('слишком маленькое'); end;
untile yournumb=mynumb;
Writeln('Угадал!');
Readln; Readln; end.
While ... do — оператор цикла с предусловием, отличается от оператора repeat ... until тем, что:
r условие проверяется до первого выполнения тела цикла;
r если условие не выполняется, цикл перестает выполняться.
Его формат:
While логическое_выражение do begin оператор(ы); end;
В листинге 8.7 представлен текст программы, в которой ввод числа (в интервале от 1 до 100) и вычитание из исходного выполняется до тех пор, пока исходное значение превышает 10.
![]()
program Demo7; var i, n: Integer; begin i:=100;
while i>100 do begin
Write('Введите число (1 – 100)');
Read(n); {ввод числа в интервале от 1 до 100} i:=i-n; {и вычитание из числа, заданного в программе} end;
Readln; Readln; end.
Операторы цикла используются также для сортировки массива и поиска элементов в массиве по заданным признакам. Например, в листинге 8.8 представлен текст программы поиска максимального элемента в массиве.
![]()
program Demo8; type
arraytype=array[1..5] of Integer; var
i, max: Integer; numb: arraytype; begin
for i:=1 to 10 do {заполнение массива элементами} begin
Writeln('Введите ', i, ' элемент'); Readln(numb[i]); end;
max:=numb[1];
for i:=2 to 10 do {поиск максимального элемента в массиве} if numb[i]>max then max:=numb[i];
Writeln;
Writeln('Максимальный элемент ', max); Readln; end.
Массив можно заполнить элементами, по крайней мере, двумя способами: ввести с клавиатуры каждый элемент (как в примерах в листингах 8.8 и 8.9) либо задать с помощью специальной функции random(r) — генератора случайных чисел (как в примерах в листингах 8.6 и 8.10). Аргументом этой функции является константа r, а значением — число, которое больше или равно нулю, но меньше r. Если использовать функцию random без аргумента, то результатом будет число в интервале [0, 1].
Есть разные способы отсортировать (упорядочить) последовательность элементов. В примерах показаны два из них: линейный (листинг 8.9) и пузырьковый (листинг 8.10).
![]()
program Demo9; type
arraytype=array[1..5] of Integer; var
i, j, temp: Integer; numb: arraytype; begin
for i:=1 to 5 do {заполнение массива элементами вводом с клавиатуры} begin
Writeln('введите', i, ' элемент');
Readln(numb[i]);
end; for i:=1 to 4 do for j:=i+1 to 5 do
if numb[i]>num[j] then {если элементы не на своих местах и нарушают порядок возрастания, они меняются местами} begin temp:=numb[i]; numb[i]:=num[j]; num[j]:=temp; end; Writeln;
for i:=1 to 5 do {вывод упорядоченного массива на экран} begin
Write(numb[i], ' '); end; Readln; end.
При линейном способе сортировки каждый элемент числового ряда сравнивается с линейной последовательностью остальных элементов, и, как только находится элемент, значение которого меньше (при сортировке по возрастанию), они меняются местами. Чтобы поменять элементы местами, используется переменная величина, куда для временного хранения помещается значение одного элемента ряда, поскольку, как только ему будет присвоено значение другого элемента, прежнее значение будет утеряно.
![]()
program Demo10; type
arraytype=array[1..5] of Integer; var
i, temp: Integer; numb: arraytype; switch: Boolean; const r=10;
begin {заполнение массива элементами с помощью генератора случайных чисел} randomize; for i:=1 to 5 do begin numb[i]:=random(r);
Writeln(i, ' элемент ', numb[i]); end; repeat switch:=false; for i:=1 to 4 do if numb[i]>numb[i+1] then begin switch:=true; temp:=numb[i]; numb[i]:=numb[i+1]; numb[i+1]:=temp; end; until switch=false; Writeln;
for i:=1 to 5 do {вывод упорядоченного элемента массива} begin
Writeln(i, ' элемент ', numb[i]); end; Readln; end.
При пузырьковом методе каждый элемент сравнивается с соседним элементом, и, при необходимости, они меняются местами, как и в предыдущем методе. Но отличие состоит в том, что вводится переменная величина логического (булева) типа, и каждый раз, как только обнаружены элементы не на своих местах, она меняет свое значение и служит «флажком», отмечающим выполнение перестановки. Элементы ряда постепенно оказываются на своих местах подобно тому, как пузырьки воздуха постепенно всплывают на поверхность. Отсюда и название — «пузырьковая сортировка». Попарное сравнение будет выполняться до тех пор, пока выполнена хоть одна перестановка. Чем меньше перестановок требуется для упорядочения ряда, тем быстрее завершится сортировка.
Чтобы алгоритм и соответствующая ему программа были более компактными, в алгоритме и в программе выделяют самостоятельные части — вспомогательные алгоритмы и оформляют в виде подпрограмм. В подпрограмму из текста программы можно выделить повторяющуюся и имеющую самостоятельное значение часть (например, ввод или вывод данных, вычисление величин и т. п.), записать ее только один раз, дать ей имя и обращаться к ней нужное количество раз. Допускается многократное обращение к подпрограмме (ее вызов) в разных местах программы. Для удобства подпрограммы обычно размещают в начале или в конце программы. Существуют две разновидности подпрограмм: про- цедуры и функции.
Формат записи заголовка процедуры: procedure имя_процедуры[(список_формальных_параметров)]; Формат вызова и выполнения процедуры:
имя_процедуры[(список_фактических_параметров)];
Параметры — это те величины, которые используются в подпрограмме, их необходимо объявлять так же, как и все величины, используемые в программе. (Как видно из записи формата процедуры, список параметров не является обязательной частью, могут быть процедуры и без параметров.)
![]() Формальные параметры — это
величины, которые используются только внутри процедуры во время ее работы и
играют роль приемника информации, поступающей извне. Такую информацию
(конкретные значения) для формальных параметров дают фактические параметры.
Формальные параметры — это
величины, которые используются только внутри процедуры во время ее работы и
играют роль приемника информации, поступающей извне. Такую информацию
(конкретные значения) для формальных параметров дают фактические параметры.
При вызове процедуры и выполнении соответствующей подпрограммы происходит замена значений формальных параметров значениями фактических. При вызовах процедуры в разных частях основной программы могут меняться имена фактических параметров, но имена формальных остаются без изменений.
Имена формальных и фактических параметров могут быть разными, но указываются в одном и том же порядке.
В листинге 8.11 представлен текст программы поиска определенной буквы во введенном слове. Сравнение букв введенного слова (признаком конца слова служит код клавиши <Enter>) с искомой буквой и подсчет количества повторений этой буквы в слове выделены в отдельную процедуру.
![]()
program Demo11; var t, a: Char;
{Подсчет количества заданных символов во введенной строке} procedure podschet(cim: Char); var c: Char; s: Integer; begin s:=0;
Writeln('Введите строку символов'); repeat Read(c); if c=cim then s:=s+1;
until c=char(13); {13 – код клавиши Enter} Writeln('Количество ', cim, ' = ', s); end;
begin t:='b';
{подсчет количества символов 'b' во введенной строке} Writeln(' подсчет ', t); podschet(t); Writeln;
a:='n';
{подсчет количества символов 'n' во введенной строке} Writeln(' подсчет ', a); podschet(a); Writeln;
Readln; Readln; end.
Оформлять подпрограммы можно и в виде функций. Формат описания функции:
function имя_функции
[(список_формальных_параметров): тип_результата]; Формат вызова функции:
Имя_переменной := имя_функции(список_фактических_параметров);
Имя функции всегда записывается справа от знака равенства, а слева от знака равенства — имя переменной, которой присваивается значение функции.
Как видно из записи формата функции, список параметров не является обязательной частью, могут быть функции и без параметров. Функция подобна процедуре в том отношении, что в нее тоже надо передавать параметры (если они имеются), заменять значения формальных параметров фактическими. Отличие в том, что функция возвращает одно-единственное значение, само имя функции временно становится переменной, в которую передается результат вычислений.
В листинге 8.12 представлен текст программы, в которой используется функция, позволяющая ставить в соответствие тому или иному номеру соответствующий цвет.
![]()
program Demo12; type number=1..5; var usern: number; f: String;
{Функция ставит в соответствие номеру определенный цвет} function numCol(n: number): String; begin case n of
1: numCol:='белый';
2: numCol:='черный'; 3: numCol:='серый';
4: numCol:='желтый'; 5: numCol:='синий'; end; end; begin
Write('Номер? '); Readln(usern);
f:=numCol(usern); {вызов функции}
Writeln('Соответствующий цвет - ', f);
Readln; Readln; end.
При вводе номера с клавиатуры его значение присваивается переменной usern, которая служит аргументом функции. Значение функции для данного аргумента — это соответствующий номеру цвет.
В современном программировании принят важный подход, который улучшает ясность и «читабельность» программ. Он носит название структурного подхода, его предложил в 70-е годы XX века выдающийся программист Э. Дейкстра. Этот подход был в дальнейшем разработан и дополнен Н. Виртом, заложившим основы структурного программирования.
Три главных принципа структурного программирования заключаются в том, что:
r любая программа представляет собой структуру, построенную из трех типов базовых конструкций (последовательное исполнение, ветвление, цикл);
r повторяющиеся фрагменты программы либо фрагменты, представляющие собой логически целостные блоки, могут оформляться в виде подпрограмм (процедур или функций);
r разработка программы ведется методом пошаговой детализации «сверху вниз».
Обычно сначала пишется текст основной программы, в которой вместо каждого связанного с ней логического фрагмента текста вставляется вызов подпрограммы, которая будет выполнять этот фрагмент. Полученная программа отлаживается и тести- руется.
Для выполнения действий над символьными и строковыми величинами существуют специальные операции и функции.
Объявление переменных типа String (строковых) выполняется согласно следующему формату:
var
str: String [количество_символов];
Способы присвоения значения переменной типа String: str1:='computer'; или
Readln(str1);
Над переменными типа String можно выполнять операцию конкатенации (сложение значений строковых переменных присоединением к концу одной строки начала следующей): str:=str1+’program’
Сложение значений строковых переменных можно выполнить также, используя функцию concat().
Формат функции: resultstr:=concat(str1, str2, ..., strn);
Для выполнения действий над строковыми переменными существуют также специальные процедуры.
Процедура delete() — удаление указанного количества символов с заданной позиции.
Формат:
delete(строка, начальная_позиция, к-во_удаляемых_символов);
Процедура insert — вставка строки в другую строку. Формат:
insert(вставляемая_строка, принимающая_строка, позиция_вставки);
Функция copy — копирование части строки. Формат:
substr:= copy(строка, начальная_позиция, количество_символов);
Функция pos — определение позиции начала подстроки в строке. Формат:
k:= pos(строка,_которую_нужно_найти, строка,_в_которой_нужно искать);
Функция length — определение длины строки (количества символов в ней).
Формат:
имя_переменной_целого_типа:=length(строка);
Функция StrToInt — преобразование строковой переменной в целую.
Формат:
имя_переменной_целого_типа:=StrToInt(строка);
В листинге 8.13 представлен текст программы, иллюстрирующей один из приемов криптографии: дан ключ к шифру, с его помощью нужно расшифровать текст. В этой программе для реализации алгоритма расшифровки используются функции обработки строковых переменных.
![]()
program Demo13; uses sysutils; type arraytype=array[1..4] of Integer; {Расшифровать слово, зашифрованное в строке a, используя шифр строки b (порядковые номера букв слова)} var size, i: Integer; a, b, c: String; m: arraytype; begin c:=''; a:='программирование'; b:='726832'; {шифр} size:=length(b); for i:=1 to size do begin m[i]:=StrToInt(copy(b, i, 1));
{выделяем номер очередной позиции и преобразуем целое в число с помощью функции StrToInt()} c:=c+copy(a, m[i], 1); {составляем слова} end;
Writeln(c);
Readln; Readln; end.
Вопросы и задания
1. Для чего предназначены среды программирования?
2. Что такое транслятор?
3. Чем отличается компилятор от интерпретатора?
4. Из каких основных элементов состоит язык программирования?
5. Что такое идентификатор?
6. В чем принципиальное различие констант и переменных величин?
7. В чем заключается «объявление» величины в программе и почему оно необходимо?
8. Каковы основные типы величин в языке Object Pascal?
9. Для чего нужны массивы?
10. Какие бывают массивы?
11. Какие типы операций используются в программах, написанных на Object Pascal?
12. Приведите примеры стандартных функций Object Pascal.
13. Какую роль играют операторы в языке программирования?
14. Что такое формат оператора?
15. Какой оператор нужен, чтобы имени величины поставить в соответствие ее значение?
16. С помощью какого оператора можно организовать в программе ввод данных с клавиатуры?
17. Какой оператор позволяет выводить на экран результат выполнения программы?
18. С помощью каких операторов можно реализовать разветвленный алгоритм?
19. Чем отличается составное условие от простого?
20. Приведите примеры алгоритмов, в которых используются различные условные операторы.
21. Какие операторы помогают реализовать циклический алгоритм?
22. Какой оператор используется тогда, когда известно количество повторений действия (или нескольких действий)?
23. Что называют телом цикла?
24. Для чего нужен параметр цикла?
25. Чем отличается цикл с постусловием от цикла с предусловием?
26. Какими способами можно заполнить массив элементами?
27. Опишите алгоритм поиска максимального (минимального) элемента в массиве.
28. Приведите примеры алгоритмов, позволяющих выполнять сортировку элементов массива.
29. Какой из этих алгоритмов является более быстрым и почему?
30. Что такое вспомогательные алгоритмы и для чего они нужны?
31. Какие части программы обычно выделяют и оформляют в виде подпрограммы?
32. Что такое процедура и функция? В чем их отличие?
33. Что такое параметры?
34. Чем отличаются фактические параметры от формальных?
35. Каковы основные принципы структурного программирования?
36. Какие процедуры и функции предназначены для обработки строковых переменных?
37. Приведите примеры использования процедур и функций для обработки строковых переменных.
38. Определите, что будет напечатано в результате работы программы:
program prim1; var
k, s: Integer; begin s:=0; k:=0; while s<1024 do begin s:=s+10; k:=k+1; end;
Write(k);
Readln; end.
39. Определите значение переменной c после выполнения программы:
program prim2; var
a, b, c: Integer; begin a:=40; b:=80; b=-a-2*b;
if a<b then c:=b-a else c:=a-2*b;
Write(c); Readln; end.
40. Составьте программу получения всех совершенных чисел из диапазона от 1 до n. (Натуральное число называется совершенным, если оно равно сумме всех своих делителей.)
41. В программе, приведенной далее, используется одномерный целочисленный массив A с индексами от 0 до 9. В ней сначала задаются значения элементов, а затем некоторые из них меняются местами.
program prim3; type arraytype=array[1..10] of Integer; var i, k, j: Integer;
A: arraytype; begin for i:=0 to 9 do begin
Writeln('i = ', i);
A[i]:=9-i;
Writeln('i = ', i, 'k = ', k, 'A(', i, ')', A[i]); end; for j:=0 to 4 do begin k:=A[j];
A[j]:=A[9-j];
A[9-j]:=k; end;
Writeln; for i:=0 to 9 do begin
Writeln('Итого i = ',i, 'k = ',k, 'A(', i, ')', A[i]); end;
Readln; end.
Какая из данных последовательностей представляет значения элементов массива после выполнения программы?
а) 9 8 7 6 5 4 3 2 1 0
б) 0 1 2 3 4 5 6 7 8 9
в) 9 8 7 6 5 5 6 7 8 9
г) 0 1 2 3 4 4 3 2 1 0
42. В программе, приведенной далее, после ввода значения x на экран выводятся значения двух переменных — L и M. Укажите наибольшее из x, при вводе которого будут выведены значения 3 и 7.
program prim4; var
x, L, M: Integer; begin
Writeln('Введите x ');
Readln(x);
L:=0; M:=0; while x>0 do begin
L:=L+1; if M<(x mod 10) then begin
M:=x mod 10; end; x:=x div 10; end;
Writeln(L);
Writeln(M);
Readln; end.
43. Определите, какое число будет напечатано в результате выполнения алгоритма, описанного приведенной далее программой?
program prim5; var
a, b, t, M, R: Integer; function F(x: Integer): Integer ; begin
F:=4*(x-1)*(x-3); end; begin a:=-20; b:=20; M:=a; R:=F(a); for t:=a to b do begin if (F(t)<R) then begin
M:=t;
R:=F(t);
Writeln('t = ', t); end; end;
Write(M);
Readln;
Readln; end.
44. Составьте программу, которая проверяет принадлежность точки с координатами (x, y) закрашенной области (рис. 8.5).
Рис. 8.5. К заданию 45
Глава 8
Р е ш е н и е.
В программе переменным s и k присваиваются нулевые значения, далее организован цикл с предусловием. Действия в теле цикла будут повторяться до тех пор, пока выполняется условие s<1024. В теле цикла два действия, заданные соответствующими рекуррентными соотношениями (s:=s+10 и k:=k+1). При каждом проходе цикла к переменной s будет прибавляться 10. Чтобы значение s стало равным 1020, нужно повторить действия 102 раза, очередное приращение приведет к тому, что значение s станет равным 1030, условие перестанет выполняться, действия в теле цикла больше не будут повторяться, и на экран будет выведено последнее значение переменной k, т. е. 103.
Ответ: 103.
Р е ш е н и е.
В программе переменным а и b присваиваются значения 40 и 80 соответственно, затем переменной b присваивается значение выражения –a–2*b. При подстановке в него исходных значений a и b получаем: b=-40-2*80=-200. Проверяется условие: поскольку a больше b, переменной c присваивается значение a-2*b=40-(-200*2)=440.
Ответ: 440.
Р е ш е н и е.
В программе, приведенной далее, должна быть предусмотрена проверка: делится ли число n на каждое из чисел в диапазоне от 1 до n – 1. Проверку можно организовать с помощью операции mod,
Программный способ записи алгоритмов
результатом которой является остаток от деления двух чисел. Если остаток равен нулю, значит, число n делится нацело. С помощью рекуррентного суммирования находится сумма делителей. После того как сумма найдена, проверяется условие равенства числа n этой сумме с выводом соответствующего сообщения.
Ответ: program prim6; var
i, n, sum: Integer; begin
Write('Введите число '); Readln(n); sum:=0;
for i:=1 to n-1 do {выделение и суммирование делителей} begin
if (n mod i)=0 then sum:=sum+i; end;
Writeln('sum = ', sum); if n=sum then Write('совершенное') else Write('несовершенное'); Readln; end.
Р е ш е н и е.
В программе сначала заполняется массив A элементами, значения которых 9, 8, 7, 6, 5, 4, 3, 2, 1, 0. Затем, в следующем цикле происходит обмен значениями между четырьмя парами элементов (первым и последним элементами, вторым и предпоследним и т. д.). В результате этого последовательность значений выстроится в обратном порядке.
Ответ: 0 1 2 3 4 5 6 7 8 9.
Глава 8
Р е ш е н и е.
Очевидно, что наибольшим числом из всех возможных вводимых чисел, при котором в качестве значений L и M будут выведены, соответственно, 3 и 7, является 777. В этой программе организован цикл с предусловием (проверкой того, превышает ли введенное число 0) . В теле цикла при выполнении этого условия переменная L каждый раз получает приращение (увеличивается на 1). Для того чтобы значение L стало равным 3, необходимо, чтобы цикл прокрутился 3 раза, т. е. переменная x должна быть равна такому трехзначному числу, при делении которого на 10 получаем в остатке 7, при делении целой части частного снова получаем 7, и затем снова — 7 (что и будет выведено в качестве значения переменной M).
Ответ: 777.
Р е ш е н и е.
В программе определяется значение функции F. Затем присваиваются значения переменным a и b, M и R, причем при вычислении значения переменной R вместо значения формального параметра x подставляется значение фактического параметра a. Таким образом, R присваивается значение выражения 4*(-20-1)*(-20-3), т. е. 1932. Далее следует цикл с параметром (который обозначен переменной t и последовательно принимает значения в интервале от –20 до 20). При каждом проходе цикла происходит подстановка очередного значения переменной t вместо формального параметра функции F и вычисляется значение этой функции. Переменной M будет присваиваться значение t, а переменной R — значение F(t), пока выполняется условие F(t)<R. Оно выполнится последний раз, когда t станет равным 2 (т. к. нетрудно подобрать значение t=1, при котором F=0, при этом R=12, при t=2 получаем F=-4 и R=0). Уже при следующем значении t=3 получаем F=0 и R=-4, и условие перестает выполняться.
Ответ: 2.
Программный способ записи алгоритмов
Р е ш е н и е.
Программа должна включать оператор ввода пары координат точки и оператор проверки условия принадлежности данной области каждой координаты. Очевидно, что –1 < x < 1, и –1 < y < 1. Эти два условия разбиваются на простые, которые объединяются логическими связками and. Полученное таким образом составное условие записывается в качестве аргумента условного оператора. Если составное условие справедливо для введенной пары координат, то будет выведено сообщение «принадлежит», в противном случае — «не принадлежит».
Ответ: program prim7; var x, y: Real; s: String; begin
Writeln('x, y - ?'); Readln(x, y);
if (x>-1) and (x<1) and (y>-1) and (y<1) then s:='принадлежит' else s:='не принадлежит';
Writeln('Данной области точка с координатами x = ', x,
', y = ', y, ' ', s); Readln; end.
|
206 Глава 8
|
Общеобразовательный школьный предмет по информатике называется «Информатика и ИКТ».
В книге сделан упор на содержание информатики как научной дисциплины, без рассмотрения прикладных технологических аспектов курса. Вопросы информационно-коммуникационных технологий достаточно подробно изучаются на базовом уровне средней школы. Теоретическая же часть по информатике в большинстве школьных пособий, включенных в «Федеральный перечень учебников, рекомендованных (допущенных) Министерством образования и науки РФ к использованию в образовательном процессе в общеобразовательных учреждениях», не всегда дается в до статочном объеме.
Изучив все темы, внимательно рассмотрев решенные задачи и самостоятельно выполнив предложенные задания, выпускник сможет успешно выполнить задания ЕГЭ. Проверить свои знания можно с помощью тестов («Открытый сегмент федерального банка тестовых заданий», задания 2011 г., 5 зачетов), размещенных на сайте http://www.fi pi.ru/view/sections/160/docs.
Другие материалы по Единому государственному экзамену можно найти на официальном информационном портале ЕГЭ (http://www.ege.edu.ru/):
1. Единый государственный экзамен по информатике и ИКТ:
Демонстрационный вариант КИМ 2011 г. см. по адресу http:// www1.ege.edu.ru/fi les/demo/demo_2011/inf_demo_2011.pdf.
2. Пробное онлайн-тестирование по информатике и ИКТ можно пройти на сайте http://www1.ege.edu.ru/online-testing/inf.
Желаем успешной сдачи ЕГЭ по информатике!
ПРИЛОЖЕНИЕ
В этом пособии представлен материал книги, дополненный интерактивными схемами, гиперссылками и анимацией — теми элементами, которые позволят читателям лучше понять предложенный в книге материал.
Для работы с компакт-диском необходим браузер Windows
Internet Explorer.
[1] На прилагаемом к книге компакт-диске имеется анимированная схема, демонстрирующая процесс работы микропроцессора при выполнении операции сложения двух чисел.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.