Интегрированная проверочная работа «Алгебра+геометрия» для классов с углублённым изучением математики. 8 класс.

Творческая  интегрированная  проверочная   работа  по темам «Линейное уравнение с 2 переменными.  Система уравнений с 2 переменными.  Теорема  Пифагора.  Подобие. Соотношения между сторонами и углами в прямоугольном  треугольнике».  Проверочная работа составлена с учётом подготовки учащихся (1 и 2 уровень сложности) для  учащихся 8 класса с углублённым изучением математики. Три варианта работ содержат творческие интегрированные задания по алгебре с учётом применения теоремы Пифагора, понятия подобия и  соотношения в прямоугольном треугольнике. 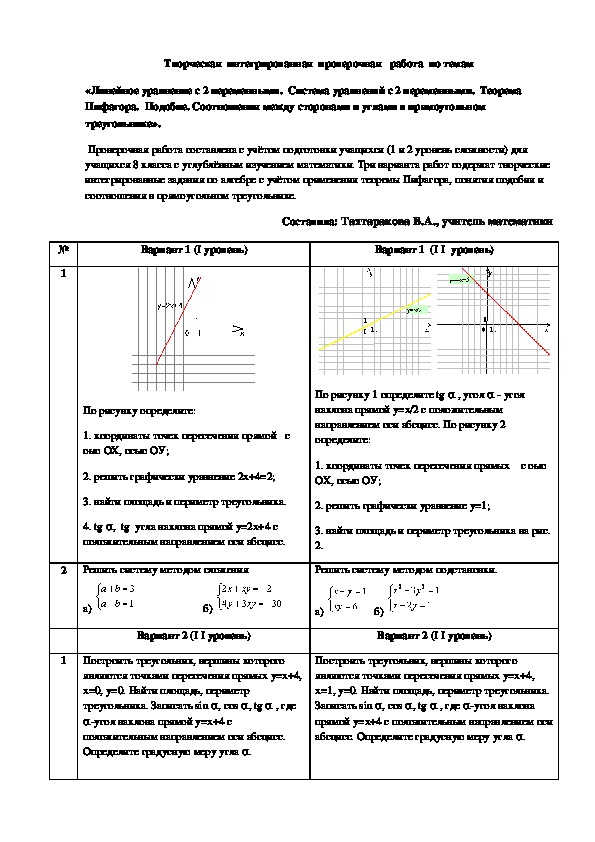Составила: Тахтаракова В.А., учитель математики Вариант 1 (I уровень) Вариант 1  (I I  уровень) № 1 По рисунку определите:  1. координаты точек пересечения прямой   с  оью ОХ, осью ОУ; 2. решить графически уравнение 2х+4=2; 3. найти площадь и периметр треугольника. 4. tg α,  tg  угла наклона прямой у=2х+4 с  положительным направлением оси абсцисс. По рисунку 1 определите tg α , угол α ­ угол  наклона прямой у=х/2 с положительным  направлением оси абсцисс. По рисунку 2  определите:  1. координаты точек пересечения прямых    с оью  ОХ, осью ОУ; 2. решить графически уравнение у=1; 3. найти площадь и периметр треугольника на рис.  2. 2 Решить систему методом сложения Решить систему методом подстановки.  а)                          б)  а)    б)  Вариант 2 (I I уровень) Вариант 2 (I I уровень) 1 Построить треугольник, вершины которого  являются точками пересечения прямых у=х+4, х=0, у=0. Найти площадь, периметр  треугольника. Записать sin α, cos α, tg α , где  α­угол наклона прямой у=х+4 с  положительным направлением оси абсцисс.  Определите градусную меру угла α. Построить треугольник, вершины которого  являются точками пересечения прямых у=х+4,  х=1, у=0. Найти площадь, периметр треугольника.  Записать sin α, cos α, tg α , где α­угол наклона  прямой у=х+4 с положительным направлением оси абсцисс. Определите градусную меру угла α. 2 1 2 3 4 Решите систему уравнений методом  алгебраического сложения: Решите систему уравнений методом алгебраического сложения:  Вариант 3 (I I уровень) Вариант 3 (I I уровень) Найти координаты вершин треугольника,  стороны которого лежат на прямых у=­3, у=х,  у=2­х.  Найдите S этого треугольника. Найти координаты вершин треугольника, стороны  которого лежат на прямых у=2, у=­х, у=х­2.  Найдите площадь этого треугольника. Найти координаты точки пересечения  графиков функций  у=­3х+7,5 и у=х+0,5 Докажите, что функция у=2­(х­1)2 +(х+2)2  является линейной. Найдите координаты точек  пересечения графика этой функции с осями  координат. Составить уравнение прямой у1=кх+в, если она проходит через точки А1(0;4) и В1(­5;0) и  уравнение прямой у2=кх+в, если она проходит  через точки А2(0;­1) и В2(3;5).  Построить эти  прямые в одной системе координат.  Сделать  выводы о взаимном расположении графиков  функций. Найти коэффициент подобия,  отношение периметров, отношение площадей  полученных подобных треугольников. Найти  площади, периметры треугольников. Составить уравнение прямой у1=кх+в, если она  проходит через точки А1(0;4) и В1(­5;0) и  уравнение прямой у2=кх+в, если она проходит  через точки А2(0;­1) и В2(3;5.  Построить эти  прямые в одной системе координат.  Сделать  выводы о взаимном расположении графиков  функций. Найти коэффициент подобия,  отношение периметров, отношение площадей  полученных подобных треугольников. Найти  площади, периметры треугольников.  Источники. 1. Изображения графиков взяты из  проекта Чореску О. А. "К чему может привести  знание свойств линейной функции"