
Иррациональные уравнения из материалов ЕГЭ профильного уровня.
1. а) Решите уравнение: ![]()
б) Найдите корни уравнения, принадлежащие отрезку [log30,5; log32].
Решение. а) Подкоренные выражения должны быть равны и неотрицательны:
![]()
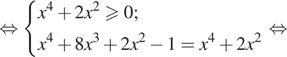
![]()
б) Заметим, что ![]() Неравенство
Неравенство
![]() является верным,
следовательно, корень
является верным,
следовательно, корень ![]() принадлежит отрезку
[log30,5; log32].
принадлежит отрезку
[log30,5; log32].
Ответ: а) ![]() б)
б)
![]()
2. а) Решите уравнение: ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Запишем
исходное уравнение в виде ![]() При
При ![]() уравнение не имеет корней. При
уравнение не имеет корней. При ![]() уравнение принимает вид:
уравнение принимает вид:
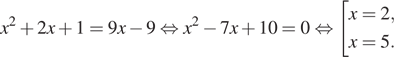
Оба корня удовлетворяют условию ![]()
б) Заметим, что ![]() Значит, указанному отрезку
принадлежит корень x = 2.
Значит, указанному отрезку
принадлежит корень x = 2.
Ответ: а) 2; 5; б) 2.
Примечание.
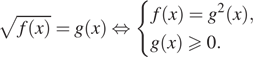
3. а) Решите уравнение ![]()
б) Укажите все корни этого уравнения, принадлежащие
промежутку ![]()
Решение. а) Решим
уравнение: ![]()
4.
а) Решите уравнение: ![]()
б) Найдите корни уравнения, принадлежащие отрезку [log30,5; log32].
Решение. а) Подкоренные выражения должны быть равны и неотрицательны:
![]()
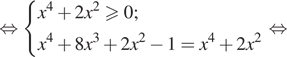
![]()
б) Заметим, что ![]() Неравенство
Неравенство
![]() является верным,
следовательно, корень
является верным,
следовательно, корень ![]() принадлежит отрезку
[log30,5; log32].
принадлежит отрезку
[log30,5; log32].
Ответ: а) ![]() б)
б)
![]()
5.а) Решите уравнение: ![]()
б) Укажите корни этого уравнения, принадлежащие
отрезку ![]()
Решение. а) Запишем
исходное уравнение в виде ![]() При
При ![]() уравнение не имеет корней. При
уравнение не имеет корней. При ![]() уравнение принимает вид:
уравнение принимает вид:
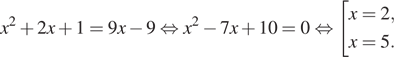
Оба корня удовлетворяют условию ![]()
б) Заметим, что ![]() Значит, указанному отрезку
принадлежит корень x = 2.
Значит, указанному отрезку
принадлежит корень x = 2.
Ответ: а) 2; 5; б) 2.
Примечание.
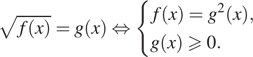
6. а) Решите уравнение ![]()
б) Укажите все корни этого уравнения, принадлежащие
промежутку ![]()
Решение. а) Решим уравнение:
![]()
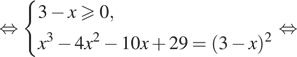
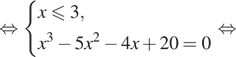
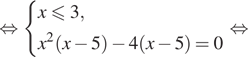

б) Поскольку ![]() отрезку
отрезку ![]() принадлежит
только число 2.
принадлежит
только число 2.
Ответ: а)![]() ; б) 2.
; б) 2.
7. а) Решите уравнение ![]()
б) Найдите решения уравнения, принадлежащие отрезку ![]()
Решение. а) Сделаем
замену переменной: ![]() Получаем
Получаем ![]() или
или ![]() Тогда:
Тогда:
![]()
Заметим, что ![]() и поэтому,
и поэтому, ![]() получаем:
получаем:
![]()
Равенство ![]() верно только для
неположительных значений a. Поэтому
верно только для
неположительных значений a. Поэтому ![]() откуда
откуда
![]()
б) В силу цепочки неравенств
![]()
![]()
из всех решений уравнения на отрезке ![]() лежат
только решения
лежат
только решения ![]()
Ответ: а) ![]() б)
б) ![]()
8. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. a) Запишем
уравнение в виде![]() и воспользуемся
тем, что
и воспользуемся
тем, что
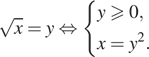
Получим:
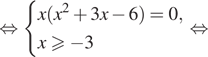
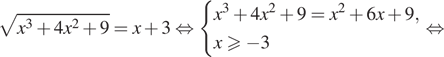
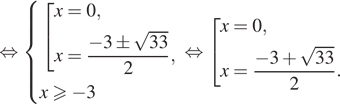
б) Число 0 принадлежит отрезку ![]() Чтобы
сравнить
Чтобы
сравнить ![]() и
и
![]() сравним разность этих
чисел с нулем:
сравним разность этих
чисел с нулем:
![]()

Значит, ![]()
Ответ: а) ![]() б)
б)
![]()
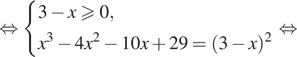
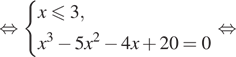
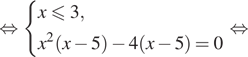
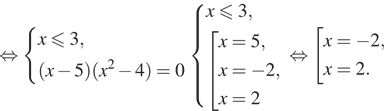
б) Поскольку ![]() отрезку
отрезку ![]() принадлежит
только число 2.
принадлежит
только число 2.
Ответ: а)![]() ; б) 2.
; б) 2.
9. а) Решите
уравнение ![]()
б) Найдите решения уравнения, принадлежащие отрезку ![]()
Решение. а) Сделаем
замену переменной: ![]() Получаем
Получаем ![]() или
или ![]() Тогда:
Тогда:
![]()
Заметим, что ![]() и поэтому,
и поэтому, ![]() получаем:
получаем:
![]()
Равенство ![]() верно только для
неположительных значений a. Поэтому
верно только для
неположительных значений a. Поэтому ![]() откуда
откуда
![]()
б) В силу цепочки неравенств
![]()
![]()
из всех решений уравнения на отрезке ![]() лежат
только решения
лежат
только решения ![]()
Ответ: а) ![]() б)
б) ![]()
10. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие
отрезку ![]()
Решение. a) Запишем
уравнение в виде![]() и воспользуемся
тем, что
и воспользуемся
тем, что
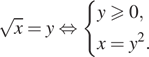
Получим:
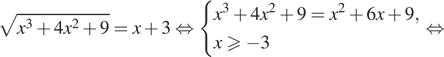
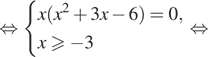
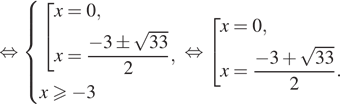
б) Число 0 принадлежит отрезку ![]() Чтобы
сравнить
Чтобы
сравнить ![]() и
и
![]() сравним разность этих
чисел с нулем:
сравним разность этих
чисел с нулем:
![]()

Значит, ![]()
Ответ: а) ![]() б)
б)
![]()
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.