Использование прогрессии для решения реальных задач прикладных характера.

 

Дата: 20.04.24 г

 

Класс: 10

 

Предмет: алгебра

Тема урока: « Использование прогрессии для решения реальных задач прикладных характера. »

 

Цели и задачи урока:

 

Образовательные: создание условий на уроке для:

обобщения и систематизации теоретических знаний по данной теме;

совершенствования навыков применения теоретических знаний при решении прикладных задач;

решения задач с использованием межпредметных связей;

преодоления в сознании учащихся представлений об оторванности данного материала от жизни и практики.

Развивающие: способствовать развитию

логического мышления, вычислительных навыков, памяти;

познавательного интереса у учащихся;

грамотной математической речи.

Воспитательные:

формулирование таких качеств личности, как ответственность, внимательность, умения анализировать;

воспитывать настойчивость для достижения конечных результатов, дисциплинированность.

Задачи учителя на уроке:

проконтролировать знания теоретического материала;

проверить навыки учащихся по применению своих знаний в ходе решения нестандартных задач;

развивать представление учащихся об использовании прогрессии в окружающей жизни;

продолжить работу над развитием логического мышления, умением анализировать, сопоставлять и обобщать полученные знания.

 

                                                 Ход урока

 

1. Организационный момент.

2. Актуализация опорных знаний.

3. Изучение нового материала.

 

        

Изучены космос и море, Строенье звезд и вся Земля.

Но математиков зовет. Известный лозунг: «Прогрессия – движение вперед».

 

Услышав обсуждение на семейном совете вопроса о вложении накопившихся средств, я была тронута непростой задачей: «Какой банк лучше выбрать, чтобы вклад был действительно, наиболее прибыльным?». Оказывается, все непросто. Походив по различным банкам нашего региона «Банк Каспийский», «Казкоммерцбанк», «Альянс-банк», «Сбербанк» и др., я собрала  рекламные визитки о вкладах и стала считать, куда выгоднее вложить средства. Через некоторое время я взялась за голову: считать вручную, сколько получиться через 1 год, через 2 и т.д. было сложно. Меня мучил вопрос: «Как же в банках так быстро операторы выдают ответы миллионам людей?» Значит, существует способ, позволяющий в один миг показать сколько на твоем счету будет в любое время. Выход из положения подсказал учитель математики, направив исследовать последовательности чисел. Изучив дополнительную литературу и интернет ресурсы по предложенной теме, я убедилась, что прогрессии играют важную роль в повседневной жизни человека и помогают решать многие «реальные» задачи рациональным путем. Я счастлива, что смогла помочь своим родителям решить такую важную проблему, как вложение накопленных средств. Мое любопытство все увеличивалось и я решила классифицировать задачи по сферам влияния на жизнь и деятельность человека, показав обширный мир прогрессий. В итоге получилось пособие, которое

ü может служить практическим руководством для решения задач из окружающего мира,

ü показывает взаимосвязь между такими смежными науками, как история, физика, химия, биология, экономика и др.

ü направлено на развитие логического мышления, на углубление знаний не только математики, но и других наук, а значит является мощным инструментом для  повышение интеллектуального уровня.

Задачи на прогрессию - это не абстрактные формулы. Они берутся из самой нашей жизни, связаны с ней и помогают решать многие практические вопросы. 

 

1.     Прогрессия в древности.

Термин “прогрессия” был введен римским автором Боэцием еще в IV в. н.э. От латинского слова progressio – “движение вперед”. Первые представления об арифметической прогрессии были еще у древних народов. В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания как их решать. Так встречается старинная задача о делении хлеба, которая записана в знаменитом египетском папирусе Ринда. Папирус этот, разысканный Риндом полвека назад, составлен около 2000 лет до нашей эры и является списком с другого, еще более древнего математического сочинения, относящегося, быть может, к третьему тысячелетию до нашей эры.

Задача о делении хлеба. Сто мер хлеба разделить между пятью людьми так, чтобы второй получил на столько же больше первого, на сколько третий получил больше второго, четвертый больше третьего и пятый больше четвертого. Кроме того, двое первых должны получить в 7 раз меньше трех остальных. Сколько нужно дать каждому?

Решение:

Очевидно, количества хлеба, полученные участниками раздела, составляют возрастающую арифметическую прогрессию. Пусть первый ее член х, разность y. Тогда

доля первого х,  доля второго х + у, доля третьего х + 2y, доля четвертого х + 3y, доля пятого х + 4y.

На основании условий задачи составляем следующие два уравнения:

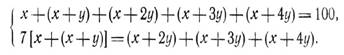
После упрощений система принимает вид

 Решив эту систему, получаем:x= ,y =. Значит, хлеб должен быть разделен на следующие части,, 20,, 38.

Уже в Древнем Египте знали не только арифметическую, но и геометрическую прогрессию. Вот, например, задача из папируса Райнда: «У семи лиц по семи кошек; каждая кошка съедает по семи мышей, каждая мышь съедает по семи колосьев, из каждого колоса может вырасти по семь мер ячменя. Как велики числа этого ряда и их сумма?»

Решение:числа7, 49, 343, 2401, 16807, 117649 представляют геометрическую прогрессию, первый член b₁= 7 и знаменатель прогрессии q=7. Тогда, используя формулу n-го члена прогрессииb_n= b₁q^n-1, находим b₆= 7 ·7^6-1= 7 ·7⁵= 7⁶= 117649.По формуле суммы n - первых членов геометрической прогрессии:S_n=(b₁(qⁿ-1))/(q-1),  находимS₆ =

 

4. Закрепление изученного материала.

 

2.     Прогрессия в математике

Задача № 1. Числа   градусов,    содержащихся   в       последовательных  внутренних   углах  некоторого многоугольника, составляют прогрессию,  разность которой 10; наименьший угол этого многоугольника 100°. Сколько в многоугольнике сторон?

Решение. S_n=(2a₁+d(n-1))∙n:2= =(200+10(n-1))∙n:2=5n²+95n. Сумма внутренних углов многоугольника находится по формуле, известной из геометрии: (n-2)·180.

5n²+95n= 180n-360;

5n²-85n+360=0;

n²-17n+72=0;

n=8,    n=9.

Существует два многоугольника, удовлетворяющих условию задачи: восьмиугольник и девятиугольник

3.     Прогрессии в промышленности

Задача № 1. Директора двух заводов А и В встретились на совещании. Из их беседы выяснилось, что оба завода выпустили за последний год одинаковые количества продукции, а именно по 1000 т металлических изделий. На совещании было решено добиваться дальнейшего роста продукции, причём был намечен ежегодный прирост на 40%.

Решение:

Директор завода А выполнял задание следующим образом. В первый год после совещания его завод выпустил на 40% больше, чем раньше, т. е. на две пятых, а именно:

1000 +1000 • 2/5 = 1000 + 400 =1400.

За второй год завод выпустил ещё на 400 т больше,

т. е.1400 + 400=1800,и так далее. В результате выпуск изделий за последующие 4 года оказался таким:

до совещания.......1000,

1-й год..........1400,

2-й »........ 1800,

3-й ».......... 2200,

4-й ».......... 2600.

Директор завода В поступил иначе. За первый год после совещания он выпустил на 40% больше, чем раньше, т. е.1000 +1000 • 2/5 =1400 т.

За второй год директор завода В добился дальнейшего роста производительности труда, и завод выпустил за второй год на 40% больше, чем за первый год:

1400 + 1400 • 2/5 = 1400 + 560 = 1960 т.

На третий год он составил план по тому же принципу: опять увеличить выработку на 40% по сравнению с предыдущим годом:

1960+ 1960 • 2/5 = 1960 + 784 = 2744 т.

За четвёртый год завод В дал такую выработку:

2744 + 2744 • 2/5 = 2744 + 1098 = 3842.

В результате выпуск изделий заводом В оказался следующим:

до совещания.......1000,

1-й год..........1400,

2-й »........ 1960,

3-й ».......... 2744,

4-й ».......... 3842.

Заметим, что коэффициент увеличения здесь равен 7/5 , так как выпуск каждого года составляет 140% предыдущего года,140%= 140/100 = 7/5 .

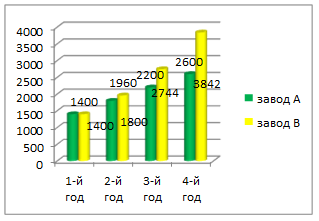         Через 4 года директоры заводов А и В снова встретились на совещании и сравнили выработку обоих заводов. Оказалось, что завод В выпустил значительно больше изделий, чем завод A.

         Завод А сохранял всё время одну и ту же надбавку, равную 400 т в год. Завод В сохранял неизменным отношение выработки двух соседних лет, т. е. коэффициент увеличения k = 7/5 .

Делаем вывод: завод А строил свой план на основе арифметической прогрессии, а завод В – на основе геометрической прогрессии:

-формула простых процентов для завода А

=3841,6- формула сложных процентов для завода В. Что намного эффективней, поэтому результат у завода В выше, чем у завода А, что видно по мониторингу.

 

 

4.     Прогрессии в биологии

Известно, что бактерии размножаются делением: одна бактерия делится на две; каждая из этих двух в свою очередь тоже делится на две, и получаются четыре бактерии; из этих четырех в результате деления получаются восемь бактерий и т. д. Результат каждого удвоения будем называть поколением.

Задача №1. Летом инфузории размножаются бесполым способом делением пополам. Сколько будет инфузорий после 15-го размножения?

Решение:b₁₅ = 2·2¹⁴ = 32 768

Способность к размножению у бактерий настолько велика, что если бы они не гибли от разных причин, а беспрерывно размножались, то за трое суток общая масса потомства одной только бактерии могла бы составить 7500 тонн. Таким громадным количеством бактерий можно было бы заполнить около 375 железнодорожных вагонов.

Задача №2.Бактерия, попав в живой организм, к концу 20-й минуты делится на две бактерии, каждая из них к концу следующих 20 минут делится опять на две и т.д. Найдите число бактерий, образующихся из одной бактерии к концу суток.

Решение. В сутках 1440 минут,  каждые двадцать минут появляется новое поколение - за сутки 72 поколения. По формуле суммы n первых членов геометрической прогрессии, у которой b₁=1, q=2, n=72, находим, что S₇₂=2⁷²-1= 4 722 366 482 869 645 213 696 - 1= 4 722 366 482 869 645 213 695(бакт).

Задача №3. В благоприятных условиях бактерия размножается так, что за 1 секунду делится на три. Сколько бактерий будет в пробирке через 5 секунд?

Решение. Составим математическую модель задачи:размножение происходит по  геометрической прогресии, у  которой b₁=1, g=3, тогда  (б).

Ответ: через пять секунд бактерий будет 121.

Интенсивность размножения бактерий используют:

	в пищевой промышленности (для приготовления напитков, кисломолочных продуктов, при квашении, солении и др.)	в фармацевтической промышленности (для создания лекарств, вакцин)
	в сельском хозяйстве (для приготовления силоса, корма для животных и др.)	в коммунальном хозяйстве и природоохранных мероприятиях (для очистки сточных вод,ликвидации нефтяных пятен

 

 

5.     Прогрессии в медицине

Задача. Больной принимает лекарство по следующей схеме: в первый день он принимает 5 капель, а в каждый следующий день — на 5 капель больше, чем в предыдущий. Приняв 40 капель, он 3 дня пьет по 40 капель лекарства, а потом ежедневно уменьшает прием на 5 капель, доведя его до 5 капель. Сколько пузырьков лекарства нужно купить больному, если в каждом содержится 20 мл лекарства (что составляет 250 капель)?

Решение. Составим математическую модель задачи:

5, 10, 15,…,40,	40,	40, 35, 30,…,5
возр а1=5 и d=5		убыв. а1=5 и d=-5

а_п=а₁+d(n-1),     

40=5+5(n-1),       

n=8,                     

S_п=  , S₈ =(5+40)·8:2=180,

180 капельбольной принимал по схеме в первый период и столько же по второй период. Всего он принял 180+40+180=400(капель), всего больной выпьет 400:250=1,6 (пузырька). Значит, надо купить 2 пузырька лекарства.

 

 

6.     Прогрессии в физике

Задача № 1.При свободном падении тело прошло в первую секунду 5м, а в каждую следующую на 10м больше. Найдите глубину шахты, если свободно падающее тело достигло его дна через 5 с. после начала падения.

Решение. В первую секунду  5м,

                      во вторую секунду 15м,

                      в третью секунду 25м,

                      в четвертую секунду 35м,

                      в пятую секунду 45м.

Всего за пять секунд 5+15+25+35+45=125(м). А используя формулу суммы n-ых членов арифметической прогрессии, вычисляем одним действием:

Ответ: глубина шахты 125м.

ü Деление ядер урана происходит с помощью нейтронов. Нейтрон, ударяя по ядру урана раскалывает его на две части. Получается два нейтрона. Затем два нейтрона, ударяя по двум ядрам, раскалывают их еще на 4 части и т.д. — это геометрическая прогрессия.

 

7.     Прогрессии в быту и в других сферах деятельности.

Задача № 1. Амфитеатр состоит из 10 рядов, причем в каждом следующем ряду на 20 мест больше, чем в предыдущем, а в последнем ряду 280 мест. Сколько человек вмещает амфитеатр?

Решение:

280=+20*9,

откуда a₁=100,

тогда*10=1900

Ответ: 1900

Задача №2. Чтобы отправить четыре бандероли, требуется четыре разные почтовые марки на общую сумму 120тенге.  Цены марок  составляют арифметическую прогрессию. Сколько стоит самая дорогая марка, если она в три раза дороже самой дешевой?

Решение: хтг- стоимость самойдешевой марки, тогда стоимость самой дорогой марки-3х, используя формулу суммы n-ых членов арифметической прогрессии имеем при n=4что по условию 8х=120, тогда х=15(тг), значит стоимость самой дорогой марки 45тг. Ответ 45тенге.

 

8.     Прогрессии в спортивной сфере деятельности.

Задача № 6. Альпинисты в первый день восхождения поднялись на высоту 1400 м, а затем каждый следующий день они проходи ли на 100 м меньше, чем в предыдущий. За сколько дней они покорили высоту в 5000 м?

Решение. Составим математическую модель задачи:    1400, 1300, …, 1400-100(n-1). a₁=1400; d=-100, S_n=5000. Надо найти n.

S_n= (2a₁+ d (n-1))n:2;

5000= (2·1400-100 · (n-1)) n:2;            Условию  задачи  удовлетворяет

10000= (2800-100 n+100) n;            n=4 ( при n=25 а_n=-1000, но а_n>0)

10000= (2900-100 n) n;                    Значит, альпинисты покорили

100 n²-2900 n+10000=0;                  высоту за 4 дня.

n²-29 n+100=0;  n=25, n=4.                  Ответ: за 4 дня.

Задача № 7. В соревновании по стрельбе за каждый промах в серии из 25 выстрелов стрелок получал штрафные очки: за первый промах — одно штрафное очко, за каждый последующий — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 7 штрафных очков?

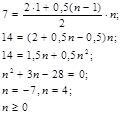Решение. Составим математическую модель задачи. Система штрафных очков составляет арифметическую прогрессию, первый член которой равен 1, а разность – 0,5.Суммапервых n членов ( количество промахов) – 7.

Найдем число промахов

Число промахов – 4. В цель стрелок попал21 раз.

9.     Прогрессии в строительстве

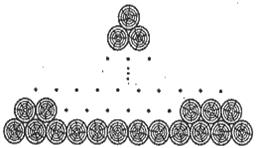Задача № 1. При хранении бревен строевого леса их укладывают как показано на рисунке. Сколько брёвен находится в одной кладке, если в ее основании положено 12 бревен?

Решение. Составим математическую модель задачи: 1, 2, 3, 4,…,12. Это арифметическая прогрессия, а₁=1, d=1,а_n=12. Надо найти n.

а_n=a₁+d(n-1); 12=1+1(n-1); n=12.

; ; S_n=78.

В одной кладке находится 78 бревен.

 Ответ: 78 бревен.

10. Прогрессии в банковских операциях

Прогрессия имеет очень широкое применение в экономике. С её помощью банки производят расчеты с вкладчиками, определяют, какие средства можно разместить в кредиты, решают, стоит ли вкладывать средства в крупные проекты, доход от которых будет получен через несколько лет и т.д. Так, вклады в банках увеличиваются по схемам сложных и простых процентов. Простые проценты – увеличение первоначального вклада в арифметической прогрессии. Сложные проценты – увеличение первоначального вклада в геометрической прогрессии.

Рассмотрим, как применяются наши знания в жизнедеятельности людей. Представьте себе, что вы открыли в банке вклад на а тенге под р% годовых на n лет. У вас есть 2 стратегии поведения: либо в конце каждого года хранения вклада снимать проценты по вкладу, то есть полученную прибыль в размере  , либо прийти в банк 1 раз – в конце срока хранения вклада. Какой доход вы получите в том и другом случаях?

Рассмотрим конкретный пример: пусть вклад составляет 10000 тенге, банк дает 10% годовых, срок хранения вклада - 5 лет. Какую сумму денег мы получим в конце срока хранения,  если выберем первую стратегию и вторую стратегию?

-А теперь вычислим эту сумму по программе, как это делают сотрудники банка(программа заранее разработана).

	1 год	2 год	3год	4 год	5 год
Первая стратегия	11000	12000	13000	14000	15000
Вторая стратегия	11000	12100	13310	14641	16105,1

Разница в конечных сумма превышает во второй стратегии на 1105,1

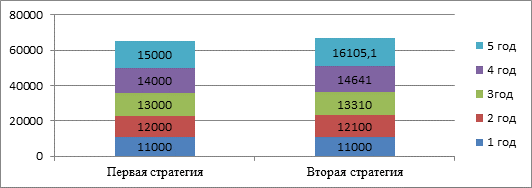
Вывод: выгоднее вторая стратегия, где начисление проводится по формуле сложных процентов.

Задача № 1.У вас образовалась прибыль в размере 100000 тенге. Есть три банка, в которые можно вложить деньги: 1-й банк – простые проценты из расчета 3% в месяц, 2-й банк-под простые проценты из расчета 40% в год, 3-й банк-под сложные проценты из расчета 30% в год. Мы хотим положить деньги на три года или пять лет. В каком банке это наиболее выгодно?

Решение: первый и второй банк работают по простым процентам( арифметическая прогрессия), а вот третий банк по сложным( по геометрической прогрессии):

I банк	II банк	III банк
Первоначальный взнос 100 000 тенге
30% годовых (простые проценты)	40% годовых (простые проценты)	30% годовых (сложные проценты)
Через три года
Вывод: на три года выгоднее положить во второй банк
Вывод: на пять  лет выгоднее положить в третий банк

 

Задача 2. Два товарища поспорили о том, что река должна покрыться льдом не ранее 20 декабря. Они условились, что если река покроется ледяным покровом раньше, то первый из них платит, а если позже, то получает за первый день 1тенге, а за каждый последующий день в 1,5 раза больше. Река покрылась льдом 12 декабря. Сколько заплатит первый? (ответ дайте в тенге, округлив до единиц)

Решение: 1 день-1 тенге, 2 день-1·1,5 тенге, 3 день-1·1,5·1,5тенге. Получаем геометрическую прогрессию, где b₁=1; q=1,5.

Соответствие дней и членов геометрической прогрессии следующее:

12 декабря-b₁ , 13 декабря-b₂ ,…, 19 декабря-b₈ . Получилось n = 8.

Применим формулу суммы и посчитаем S₈: S₈ =1·(1,5⁸­-1)*2  = 49,26 ≈ 49 (тг)

Ответ: 49 тенге

Прогрессии в хозяйстве

Задача.В огороде 30 грядок, каждая длиной 16 м и шириной 2,5 м. Поливая грядки, огородник приносит вёдра с водой из колодца, расположенного в 14 м от края огорода и обходит грядки по меже, причём воды, приносимой за один раз достаточно только для поливки одной грядки. Какой длины путь должен пройти огородник, поливая весь огород? Путь начинается и кончается у колодца.

Решение: для поливки первой грядки надо пройти 14+16+2,5+16+2,5+14=65 м

Для поливки второй грядки надо пройти 14+2,5+16+2,5+16+2,5+2,5+14=65+5=70 м

Каждая следующая грядка требует пути на 5 м  длиннее предыдущей. Имеем прогрессию: 65;70;75;…;65+5*29

Сумма её членов равна

 

Ответ: огородник проходит 4125м.

 

5. Подведение итогов урока.

В процессе иследования литературы и  интернет- ресурсов можно сделать вывод, что сами по себе прогрессии известны так давно, что нельзя говорить о том, кто их открыл.

Убеждения в том, что задачи на прогрессии, дошедшие до нас из древности, также как и многие другие знания по математике, были связаны с запросами хозяйственной жизни: распределение продуктов, деление наследства и другими, говорят о том, что с можно решить много задач с помощью формул арифметической и геометрической прогрессии. Многие жизненно-важные процессы в физике, биологии, медицине протекают по законам прогрессии. Исследование алгоритмов решения  задач литературного, исторического и практического содержания действительно показывает, что чаще всего рациональный и эффективный способ решения основан на применении прогрессий и их  свойств. Заметили, что арифметическая прогрессия в практических задачах встречается чаще геометрической. Исследования показали, что интенсивное размножение бактерий в геометрической прогрессии широко применяется в пищевой промышленности, в фармакологии, в медицине, в сельском и коммунальном хозяйствах. В банковских расчетах (начисление простых и сложных процентов) без знания прогрессии невозможно. А значит,  мы убедились в большой практической значимости таких понятий,  как арифметическая и геометрическая прогрессии. Увидели ,как применяются прогрессии  в жизни людей, научились легко и быстро вычислять необходимые компоненты реальных ситуаций, испробовали себя в роли сотрудников банка. Итак, делаем вывод:

В нашей жизни многое очевидно с помощью математики, в частности, арифметической и геометрической прогрессий. Для того,  чтобы не попадать в неудачные ситуации,  надо остановиться и подумать можно ли предугадать результат. Мы рассмотрели несколько сфер деятельности человека и убедились в том, что применение математики в жизни поможет как избежать многих проблем, так и решать их эффективными и рациональными путями.

 

 

6. Домашнее задание: