Использование различных дидактических методов при обучении младших школьников приемам сложения и вычитания

Изучение приемов сложения и вычитания чисел в пределах 10.

В начальном курсе математики изучение вычислительного приема происходит после того, как школьники усвоят его теоретическую основу (определения арифметических действий, свойства действий и следствия, вытекающие из них). Причем в каждом конкретном случае учащиеся осознают сам факт использования соответствующих теоретических положений, лежащих в основе вычислительного приема,  конструируют различные приемы для одного случая вычислений, используя различные теоретические положения.

С позиций традиционного обучения основным способом введения нового вычислительного приема является показ образца действия.

Приемы:

1.      присчитывания и отсчитывания по 1

2.      присчитывания и отсчитывания группами для случаев а + - 2, 3, 4

3.      сложение вида а + 5, 6, 7, 8, 9

4.      приема вычитания вида а – 5, 6, 7, 8, 9.

Подготовительная работа: раскрытие конкретного смысла действий сложения и вычитания, запись и чтение примеров, случаи вида «+, - »1, где результаты находятся на основе свойства натурального ряда. Начинается с первых уроков рассмотрения нумерации.

Методические приемы:

Практическая работа с предметными картинками на объединение множеств и удаление подмножества из множества.

Например:

а) положи слева 5 синих кружков, справа 3 красных кружка. Придвинь кружки друг к другу. Что ты сделал? Выполнил действие сложение.

б) объединение в вазы, корзины, гаражи…

положи на парту 5 квадратов, убери 3 квадрата. Выполнил действие вычитания. При сложении предметов становится больше, при вычитании – меньше.

Этапы рассмотрения вычислительных приемов:

1)подготовительные упражнения;

2)введение приемов вычисления;

3)закрепление знания приемов, выработка вычислительного навыка;

4)составление и заучивание таблиц.

Методические приемы:

1.      Решение выражений, иллюстрируя действия предметными картинками.

2.      Решение выражений при помощи натурального ряда

практическая работа

·         сколько всего кругов? Как узнали? 3 + 2 = 5

Поменять круги местами. 2 + 3 = 5

3.      Сравнение выражений

3 + 2                                          4 + 3

2 + 3                                          3 + 4

Сравнить значение сумм? Чем сходны, отличаются?

4.      Решение задач практического характера.

Табличное сложение однозначных чисел.

При формировании вычислительных навыков табличного сложения и вычитания учителя используют подход, характерный для традиционной системы: школьники выучивают таблицы сложения и вычитания и закрепляют их в процессе решения примеров. Познавательная деятельность учащихся в этом случае характеризуется активной работой памяти и напряжением произвольного внимания. Такой подход не обеспечивает формирование прочных и осознанных вычислительных навыков.

Программы развивающего обучения (под ред. Н.Ф. Виноградовой, Н.Б.Истоминой и др.) реализуют более эффективный подход, при котором учащиеся знакомятся с различными вычислительными приемами, самостоятельно составляют таблицы, дается установка на запоминание таблиц, а непроизвольное запоминание их происходит в процессе выполнения различных вычислительных упражнений, активно используя приемы умственных действий (анализ, синтез, сравнение, обобщение, классификация, аналогия).

Упражнения.

1.

По какому признаку разбили фигуры на две группы?

4+4=8,   6+2=8,   5+3=8.

2. По какому правилу записан каждый ряд чисел?

а). 1, 3, 2, 4, 3, 5, 4, 6:

б).2, 5, 3, 6, 4, 7, 5, 8, 6:

3.Что могут на рисунке обозначать цифры 4, 2, 8, 9, 1?

4. Запиши верные равенства, используя числа 3, 8, 5.

5. Запиши верные равенства используя числа 7, 3, 4, 1.

6. Вставь пропущенные числа.

8-6=:+:,     5+2=:+:,

9-4=:+:,     8-4=:+:.

7. Вместо точек поставь числа.

:-:=:+:,     :+:=:+:,

:+:=:-:,     :-:=:-:.

Никулина А.Д. указывает на значимость устных упражнений. Например, можно проводить игру с хлопками, когда учитель называет примеры с правильными и неправильными ответами. В случае правильных ответов дети хлопают, если ответы неправиль­ные, не хлопают. Эффективно применение карточек с записанными примерами на сложение и вычитание. Учитель показывает карточку с примером, а учащиеся поднимают карточку с ответом.

Изучение сложения и вычитания чисел в пределах 20.

Приемы:

1.      Сложение однозначных чисел (вида 9 + 3) с переходом через разряд.

2.      Прибавление однозначного к двузначному (вида 13+4).

3.      Вычитание однозначного числа из двузначного (вида 12 – 5).

4.      Вычитание однозначного из двузначного (вида 19-6).

1.      Сложение и вычитание чисел с переходом через разряд

Прием сложения включает следующие операции:

·         первая операция связана с дополнением большего слагаемого до числа 10;

·         вторая – связана с представлениями учащимся о смысле действий сложения и вычитания и с усвоением ими состава однозначных чисел. Опираясь на эти знания, учащиеся отвечают на вопрос – Сколько единиц осталось во втором слагаемом после выполнения первой операции;

·         третья операция – оставшиеся единицы второго слагаемого прибавить к 10.

Подготовительная работа:

-состав однозначных чисел;

-дополнение однозначных чисел до 10 (   +   = 10)

-решение выражений вида 6 + 4 + 3; 8 + 2 + 5

-решение выражений вида 10 + 2; 4 + 10

Методические приемы:

1.      Показ образца: Прием представляют детям в виде тождественных преобразований, используем сочетательное свойство (прибавление суммы к числу).

9 + 3 = 9 + (1 + 2) = (9 + 1) + 2= 10 + 2 = 12

Практика показывает, что семилетние дети с трудом воспроизводят такую громоздкую запись, поэтому целесообразно использовать другие формы записи:

9 + 3 = 12                                                         9 + 3 = 12

   1 + 2                                                               9 + 1 + 2

Прием «Лучики»

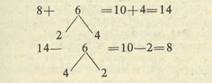
2.      Практическая работа (абак) дополнить 9 кругов до 10

-сколько осталось прибавить?

-что сделали со II слагаемым? (разбили)

-записать математически.

б) рассмотрение каждого случая 11, 12, 13, 14, 15, 16, 17, 18.

в) составление таблицы (20 случаев).

Она включает сложение одинаковых слагаемых 6 + 6      7 + 7    8 + 8    9 + 9 и прибавление меньшего числа к большему. Для прибавления большего числа к меньшему используется переместительное свойство сложения.

Особое затруднение у школьников вызывает сложение однозначных чисел с переходом через десяток, которое обусловлено количеством операций: замена числа суммой удобных слагаемых, прибавление суммы к числу, дополнение однозначного числа до 10.

Для преодоления затруднений перед изучением данной темы рекомендуем подготовительные упражнения, которые осуществляют комплексную подготовку учащихся к изучению сложения чисел для случаев вида 9+5.

1. Решите примеры удобным способом:

8+(2+3),   9+(1+4),   7+(3+4).

Почему удобно прибавлять первое слагаемое, а потом второе?

Сколько всего прибавили? А как прибавляли?

2. Объясните, сколько осталось еще прибавить в каждом примере, если всего нужно прибавить, например, 6:

8+(2+:),   9+(1+:),   6+(4+:).

3. Объясните, какой суммой удобнее заменить данное число, (например, 5), если 6+(:+:), 7+(:+:), 8+(:+:), 9+(:+:).

Данные разнообразные задания содержат комплекс вопросов, с помощью которых дети повторяют правило прибавления суммы к числу, состав чисел первого десятка, дополнение однозначных чисел до 10, а также при этом рассуждают.

3.      Вычитание однозначного числа из двузначного (вида 12 – 5).

Обычно используют 2 вычислительных приема. По своей сути они знакомы учащимся.

В основе первого лежит понятие о взаимосвязи суммы и слагаемых и прочное знание таблицы сложения и вычитания в пределах 20.

В состав этого приема входят операции:

а)представление уменьшаемого в виде суммы двух слагаемых, одно из которых равно вычитаемому;

б)вычитание из данной суммы слагаемого, равного вычитаемому, в основе правило – если из суммы вычесть I слагаемое = II слагаемое.

Второй прием - отсчитывание по частям.

а)вычитание из данного двузначного числа его разрядных единиц (результат = 10)

б)представление вычитаемого в виде суммы слагаемых, одно из которых равно количеству разрядных единиц двузначного числа (в основе операции – знание состава однозначных чисел)

в)вычитание из 10 второго слагаемого этой суммы.

подготовительная работа:

-состав чисел второго десятка

-состав однозначных чисел

-решение выражений вида 12 – 2, 18 – 8,

-решение выражений вида 15 – 5 – 2, 16 – 6 – 3.

I прием: 12 – это 5 и 7            5 + 7 = 12,                  12 – 5 = 7

II прием: 12 – 2 – 3 = 7

4. Приемами вычислений в пределах второго десятка без перехода через десяток.

Для ознакомления учащихся со сложением и вычитанием вида 15+3 и 15—3 вначале важно показать содер­жание вычислительных приемов с помощью записи всей последовательности операций действий:

15+3= (10+5)+3=10+(5+3) = 10+ +8=18

15—3= (10+5) —3= 10+ (5—3) = 10+ +2=12

При объяснении способа сложения или вычитания чисел обращается внимание на то, что операции выполняются в данном случае только над единицами, а десятки пере­носятся в ответ. Здесь удобно пользоваться опорным сигналом «рамка». Запись примеров может быть более или менее развернутой. Для самоконтроля учащиеся могут воспользоваться таблицей чисел от 1 до 20:

1 2  3  4  5  6  7  8  9  10  11  12 13  14  15  16  17  18  19  20

«Шагая» по числам таблицы, учащиеся проверяют правильность сложения или вычи­тания в пределах второго десятка.