Использование закона сохранения механической энергии при решении задач по механике

Использование закона сохранения механической энергии

 при решении задач по механике

З.М.Кенжаев

МБОУ СОШ с. Константиновка Николаевского района Хабаровского края

(zmken1975@yandex.ru)

       При применении закона сохранения механической энергии для решения задач надо, прежде всего, выяснить, какое состояние системы целесообразно считать начальным, а какое — конечным, затем записать выражение для начальной энергии системы и приравнять его выражению для конечной. При записи потенциальной энергии надо предварительно выбрать нулевой уровень отсчёта потенциальной энергии системы. Если известно положение тела и его скорость в определенный момент времени, то знание сохраняющихся величин позволяет определить положение и скорость этого тела после любого взаимодействия, не прибегая к законам динамики.

Пример 1. Шар массой 1 кг, подвешенный на нити длиной 90 см, отводят от положения равновесия на угол 60^°и отпускают. В момент прохождения шаром положения равновесия в него попадает пуля массой 10 г, летящая навстречу шару со скоростью 300 м/с. Она пробивает его и вылетает горизонтально со скоростью 200 м/с, после чего шар продолжает движение в прежнем направлении. На какой максимальный угол отклонится шар после попадания в него пули? (Массу шара считать неизменной, диаметр шара – пренебрежимо малым по сравнению с длиной нити).

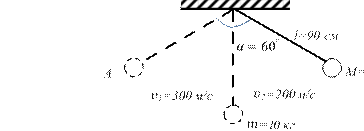
Решение. Из закона сохранения механической энергии находится скорость шара в нижней точке до попадания пули: .

Из закона сохранения импульса определяется скорость шара в нижней точке после попадания и вылета пули:

.

Закон сохранения механической энергии для шара после попадания и вылета пули:

.

Следовательно, угол отклонения определяется равенством:

,

или

.

Пример 2. На космическом аппарате, находящемся вдали от Земли, начал работать реактивный двигатель. Из сопла ракеты ежесекундно выбрасывается 2 кг газа  со скоростью v=500 м/с. Исходная масса аппарата М=500 кг. Какой будет скорость v₁ аппарата через t=6 с после старта? Начальную скорость аппарата за время движения пренебречь.

Решение. Закон сохранения импульса для системы “аппарат+газ, выброшенный за интервал времени ∆𝑡”: 

формула для ускорения  ; формула для скорости движения аппарата: 𝑣₁ = 𝑎𝑡.

Выполнив математическое преобразования, получим ответ в общем виде:

.

Ответ: 12 м/с.

Пример 3. Начальная скорость снаряда, выпущенного вертикально вверх, равна 300 м/с. В точке максимального подъема снаряд разорвался на два осколка. Первый осколок массой т₁ упал на землю вблизи точки выстрела, имея скорость в 2 раза больше начальной скорости снаряда, второй осколок массой т₂ имеет у поверхности земли скорость 600 м/с. Чему равно отношение масс    этих осколков? Сопротивлением воздуха пренебречь.

Решение. Согласно условию задачи, снаряд и оба осколка двигались вдоль одной вертикали.

Согласно закону сохранения механической энергии, если оба осколка имели одинаковую скорость при падении на землю, то их скорость бқла одинакова и в любой точке их общего участка траекторий, в том числе и в точке взрыва снаряда; второй  осколок возвративщись в точку взрыва, имел такую же по модулю скорость, какая была у него в момент взрыва.

Следовательно, при взрыве неподвижно зависшего снаряда оба осколка приобрели одинаковые по модулю, но противоположные по направлению скорости.

Согласно закону сохранения импульса, это означает, что массы осколков равны.

Ответ:.