Исследование функции с помощью производной на экстремумы.

Исследование с помощью производной.

на экстремумы.

Нахождение экстремумов ( максимумов и минимумов) функции.

Краткая теория

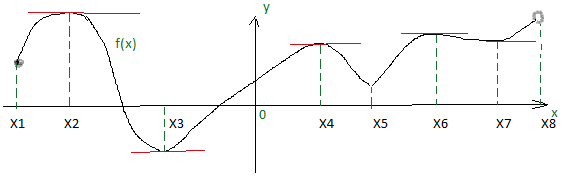
 Рисунок 1.  Рассмотрим внутренние точки области определения функции, изображенной на рис.1, в которых производная равна нулю или не существует. В точках, где производная равна 0, касательная параллельна оси ОХ. Это точки Х₂, Х₃, Х₄, Х₆ и Х₇.  В точке Х₅ касательную провести нельзя, т.к. острый график, поэтому в этой точке производная не существует.  На концах промежутка в точках Х₁ и Х₈ тоже касательные провести нельзя, так как нужна окрестность точки. На концах промежутка экстремумов не бывает.

Определение.  Точки, в которых производная функции равна 0 или не существует называются критическими.

На нашем  рисунке это точки Х₂, Х₃, Х₄, Х_5, Х₆ и Х₇.  Среди этих точек могут быть точки максимума ( max )и  минимума( min ), которые называются точками экстремума       ( X_maxи X_min ). Значения функции в этих точках называют экстремумами функции   и обозначают f_max (X_max)  и  f_min (X_min).

Необходимым условием существования экстремумов является равенство нулю производной или  производная не существует, то есть необходимое условие – это наличие критических точек. (Это теорема Ферма), но этого условия еще не достаточно. Чтобы функция имела экстремум в некоторой точке, надо, чтобы при переходе через эту точку производная меняла свой знак, то есть надо, чтобы возрастание менялось на убывание, или убывание на возрастание. Если такой смены нет, то в этой критической точке не будет экстремума.

Если знак производной меняется с  (+ ) на (- ) – это точка max, если знак производной меняется с  (- ) на (+ ) – это точкаmin.

На рис.1:  Точка Х₂ является точкой max, т.к. при переходе через эту точку возрастание сменилось убыванием ( f´(x) поменяла знак с  (+ ) на (- )). Такими же будут точки  Х₄и Х_6.             В точках Х₃и Х₅ при переходе  f´(x) поменяла знак с  (- ) на (+ ). Это точки min.

В  критической точке Х₇ не произошло смены знака производной ( функция возрастала до этой точке и после нее). Здесь никакого экстремума нет. Это просто точка перегиба. Не будет существовать экстремумов и в точках, в которых график функции будут разрываться. На нашем рисунке такого случая нет.

Вывод. Для существования экстремумов необходимо выполнение двух условий:

1. Существование критический точек.
2. Смена знака производной при переходе через критическую точку.

Нахождение экстремумов функции осуществляют по следующему плану:

1.      Найти область определения функции.

2.      Найти производную.

3.      Найти критические точки ( приравнять производную к нулю).

4.      На числовой прямой отметить найденные критические точки, выделить            полученные числовые промежутки и проверить знак производной в каждом из них.

5.      Записать, где получились точки максимума или минимума, (а может быть и перегиба, если знак производной не менялся при переходе через точку, или разрыва).

6.      Вычислить значение  экстремумов функции (значение самой функции в точках экстремума.

7.      Для наглядности или когда надо построить график заданной функции, занести все полученные данные в таблицу.

Рассмотрим примеры.

Пример 1. Найти критические точки функцииf(x) =x³ -7x² -5x +6 (в ответ записать большее значение).Решение.

(В данном примере надо выполнить только три первых пункта плана.)

1. D( f )= (- ∞; + ∞).
2. Найдем производную f ´(x) =(x³ -7x² -5x +6)´ =3х² – 14х -5
3. 3х² – 14х -5=0      D= (-14)² - 4·3·(-5) = 196 + 60 = 256 = 16²

X₁ = (14+16)/(2·3) = 5      X₂ = (14 - 16)/(2·3) = - 1/3     Ответ: 5

Пример 2.Исследовать функциюf(x) =2x³ - 24x на экстремумы ( сделать таблицу, в ответ записать а) точку минимума; б) максимум функции).

Решение.

(В этом задании надо выполнить все пункты плана.)

1. D( f )= (- ∞; + ∞).
2. Найдем производную f ´(x) =(2x³ - 24x)´= 6х² – 24
3. 6х² – 24=0Здесь неполное квадратное уравнение, вынесем за скобки общий множитель  6 (х² – 4)=0;    х² – 4=0;     х² = 4;     х₁ =2 и х₂= - 2  это критические точки.  4. Знаки в промежутках определяют,  выбирая любые числа из каждого промежутка и подставляя в производную. Например, из промежутка ( -∞; -2) можно взять число         х= - 3.        6· (-3)² -24 = 6· 9 -24=30 > 0  (если квадратичная функция, знаки чередуются).          Пункт 5 .   Xmax = -2     Xmin = 2

6. f_max(-2) =2·(-2)³ - 24·(-2)=32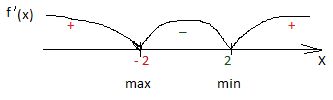

f_min(2) =2·(2)³ - 24·(2)= - 32

7.

X	( -∞; -2)	-2	(-2; 2)	2	(2 ; +∞)
f ´ (x)	+	0	-	0	+
f (x)	↑	32	↓	-32	↑
		max		min

Ответ:   а)  2               б)  32.

Пример 3.Исследовать функциюf(x) = Х+(1/х)на экстремумы ( сделать таблицу, в ответ записать  а) критические точки; б)  точку максимума; в) минимум функции).

Решение.

(В этом задании надо выполнить все пункты плана.)

1.      D(f ) = (- ∞; 0)  U (0; + ∞).      ( так как 1/х,    х≠0)

2.      Найдем производную f ´(x) =(Х +(1/х))´=1- (1/х²) = (х² -1) / х²

3.       (х² -1) = 0     х² =1      x₁ = -1   x₂ =1  при х=0 производная не существует.Критических точек 3. Это  -1; 0; 1.  Пункт 4.

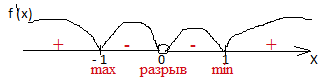Здесь функция не квадратичная функция и знаки надо проверять в каждом  промежутке.  Например, из промежутке   ( -1; 0) можно взять х= - 0,5.    1 - (1 / х²) = 1 – (1 /( - 0,5)²) = 1 –( 1/0,25)=  1 – 16 =-15 <0 ( поставили на рисунке знак минус.). Так проверяем знак в каждом промежутке в этом задании.

5.В этом примере две точки экстремума   Xmax = -1Xmin = 1

6. f_max(-1) =-1 +(1/-1)= -2

f_min(1) =1 +(1/1) = 2

7.

X	( -∞; -1)	-1	(-1; 0)	0	(0 ; 1)	1	(1 ; +∞)
f ´ (x)	+	0	--	Не существует	-	0	+
f (x)	↑	- 2	↓		↓	2	↑
		max		разрыв		min

 

Ответ:  а)  -1;  0;  1.          б)  - 1.         в)  2.

Пример 4. Найти точку минимума функции   f(x) =e ^x+1 ·x⁵

1.  D( f )= (- ∞; + ∞).

 2.  Найдем производную f ´(x) =( e ^x+1 ·x⁵)´ =( e ^x+1) ´ ·x⁵+  e ^x+1 ·(x⁵)´= e ^x+1 ·x⁵+ e ^x+1 ·5x⁴  = e ^x+1 ·x⁴(x+5).     3.  e ^x+1 ·x⁴(x+5) =0, e ^x+1 ≠0 (показательная функция), x⁴ =0  х=0,  х+5=0      х= -5.  Это критические точки. Отметим найденные точки на числовой прямой и проверим знак производной в каждом из трех получившихся промежутков.

 

 

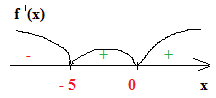
f ´(-6) = e ^-6+1 ·(-6)⁴(-6+5);   e ^-5   >0 ,(-6)⁴ >0, -1 <0 , f ´(-6) <0.

f ´(-1) = e ^-1+1 ·(-1)⁴(-1+5); e ⁰ =1 >0, ,(-1)⁴ >0,   4>0,  f ´(-1) >0.

f ´(1) = e ¹⁺¹ ·(1)⁴(1+5); e ²  >0, ,(1)⁴ >0,   6>0,  f ´(1) >0

В точке х = - 5 производная f ´(x) меняет знак с (-) на (+) ,точка х = - 5 – точка минимума. В точке х=0 производная не меняет свой знак – это точка перегиба.  Х_min = -5         Ответ: -5.

 

Исследование функции по графику ее производной.

В предыдущих заданиях осуществлялось исследование функции по ее графику. В этих примерах задавался график функции, на котором было видно, где функция возрастает, где убывает, где у нее  максимумы или минимумы. Если  задается график не самой функции, а ее производной, то в таких примерах для ответа на вопросы, надо применить изученную теорию.

Пример 5. Задан график производной некоторой функции. По графику ответить на вопросы.(цветных линий на исходном графике нет, проведены позже). 

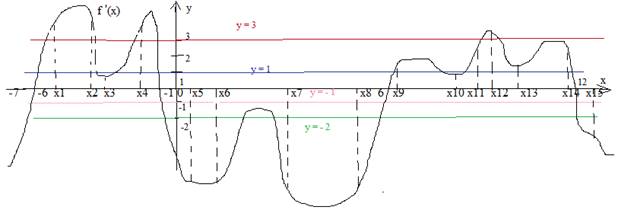
Вопросы.

1.      Сколько точек, где касательная к графику функции (не к графику производной) параллельна оси ОХ.

По условию касательная параллельна оси ОХ, значит, производная в этих точках равна нулю f  ´(x) =0. На графике функции это точки экстремума, а на графике производной, который у нас задан, это точки пересечения с осью ОХ.Надо подсчитать, сколько  таких точек. Это точки Х= - 6, Х= -1, Х=6, Х=12.

Ответ:  4

2.      а)Сколько точек, где касательная к графику функции (не к графику производной) параллельна прямым  у =  - 8 или у = - 0,5 или у =10.

б) найти сумму абсцисс этих точек.

а) Для всех этих прямых угловой коэффициент равен 0 (в уравнении касательной у=кх + b множитель, стоящий перед Х отсутствует, т.е. к =0). f  ´(x₀) = 0на графике функции это точки экстремума, а на графике производной, который у нас задан, это точки пересечения с осью ОХ.Надо подсчитать, сколько  таких точек. Это точки Х= - 6, Х= -1, Х=6, Х=12.  а)Ответ:   4

б) Подсчитаем сумму абсцисс этих точек   - 6+ (- 1)+6 +12 =11.

б)Ответ:   11

3.    Количество экстремумов функции.

В точках экстремума производная равна нулю и меняет знак при переходе через это точку. Х= - 6, Х= -1, Х=6, Х=12.

Ответ:  4

4. а)  Количество точек максимума, б) Сумма абсцисс точек максимума.

Максимум функции бывает в тех точках, при переходе через которые производная меняет свой знак с плюса на минус. (т.е. до этой точки график находился выше оси ОХ, а после этой точки график лежит ниже оси ОХ.). В нашем примере это точки Х= -1 и  Х=12. В этих точках производная поменяла знак с (+) на ( - ).       а)Ответ:   2

б) Подсчитаем сумму абсцисс этих точек   - 1 + 12 = 11.    б)Ответ:   11

5. а)  Количество точек минимума, б) Сумма абсцисс точек минимума.

Минимум функции бывает в тех точках, при переходе через которые производная меняет свой знак с  минуса на плюс. (т.е. до этой точки график находился ниже оси ОХ, а после этой точки график лежит выше оси ОХ.). В нашем примере это точки Х= -6 и  Х=6. В этих точках производная поменяла знак с (-) на ( + ).       а)Ответ:   2

б) Подсчитаем сумму абсцисс этих точек   - 6 + 6 = 0.    б)Ответ:   0

6. Наименьшая точка максимума.

Точки  максимума Х= -1 и  Х=12. Наименьшая Х= -1.Ответ:   - 1

7.  Наибольшая точка минимума.

Точки  минимума Х= -6 и  Х=6. Наибольшая Х= 6.Ответ:   6

8.   В какой точке на промежутке [ -1;6 ] функция принимает свое  а) наибольшее значение, б) наименьшее значение.

а) На промежутке [ -1;6 ] график производной находится ниже оси ОХ. На этом промежутке производная отрицательна,  сама функция убывает и ее график пойдет вниз.  Наибольшее значение примет в т. Х= -1, наименьшее значение в т. Х= 6.         а)Ответ:   -1 б)Ответ:  6

9.   В какой точке на промежутке [ 6 ; 12 ] функция принимает свое  а) наибольшее значение, б) наименьшее значение.

а) На промежутке [ 6;12 ] график производной находится выше оси ОХ. На этом промежутке производная положительна,  сама функция возрастает и ее график пойдет вверх.  Наибольшее значение примет в т. Х=12, наименьшее значение в т. Х=6а)Ответ:  12б)Ответ:  6

 

По графику ответить на вопросы.

1.

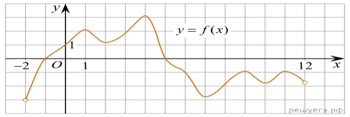На рисунке изображен график функции y  =  f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).

Решение. Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7, 10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.

 Ответ: 44.

2. 

На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].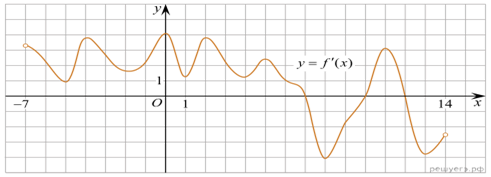

Решение. Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [−6; 9] функция имеет одну точку максимума x  =  7.       Ответ: 1.

Ответ: 1

27494

1

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.1.1 Понятие о производной функции, геометрический смысл производной, 4.2.1 Применение производной к исследованию функций и построению графиков

Ответ: 1

27495

1

Источник: Пробный экзамен Санкт-Петербург, 11.04.2017. Вариант 2.

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.1.1 Понятие о производной функции, геометрический смысл производной, 4.2.1 Применение производной к исследованию функций и построению графиков

3.

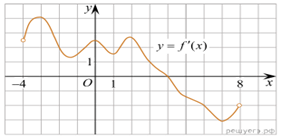
На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].

Решение. Если производная в некоторой точке равна нулю и меняет знак, то это точка экстремума. На отрезке [−2; 6] график производной пересекает ось абсцисс, производная меняет знак с плюса на минус. Следовательно, точка 4 является точкой экстремума.

 Ответ: 4.

Ответ: 4

27502

4

Источник: ЕГЭ по математике. Основная волна 07.06.2021. Урал

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции, 4.1.1 Понятие о производной функции, геометрический смысл производной, 4.2.1 Применение производной к исследованию функций и построению графиков

4.

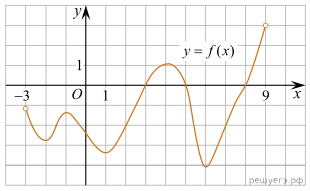На рисунке изображен график функции y  =  f(x), определенной на интервале (−3; 9) . Найдите количество точек, в которых производная функции f(x) равна 0.

Решение. Производная изображенной на рисунке функции f(x) равна нулю в точках экстремумов: −2; −1; 1; 4 и 6. Производная равна нулю в 5 точках.

 Ответ: 5.

5.

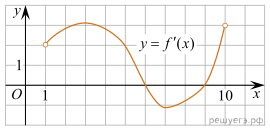На рисунке изображён график функции   — производной функции f(x) определённой на интервале (1; 10). Найдите точку минимума функции f(x).

Решение. Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. На интервале (1; 10) функция имеет одну точку минимума x  =  9.

 

Ответ: 9.

6.

Функция y  =  f (x) определена и непрерывна на отрезке [−5; 5]. На рисунке изображён график её производной. Найдите точку x₀, в которой функция принимает наименьшее значение, если f (−5) ≥ f (5).

Решение. Напомним, что если функция непрерывна на отрезке [a; b], а её производная положительна (отрицательна) на интервале (a; b), то функция возрастает (убывает) на отрезке [a; b].

Тем самым функция f, график производной которой дан в условии, возрастает на отрезках [−5; −3] и [3; 5] и убывает на отрезке [−3; 3].

Из этого следует, что f принимает наименьшее значение на левой границе отрезка, в точке −5, или в точке минимума х_min  =  3. В силу возрастания f на отрезке [3; 5] справедливо неравенство f (5) > f (3). Поскольку по условию f (−5) не меньше, чем f (5), справедлива оценка f (−5) > f (3).

Таким образом, наименьшего значения функция f достигает в точке 3. График одной из функций, удовлетворяющих условию, приведён на рисунке.

 Ответ:3.

 

9.

 

Ответ: 3

505119

3

Источник: ЕГЭ 28.04.2014 по математике. Досрочная волна. Вариант 2.

Кодификатор ФИПИ/Решу ЕГЭ: 3.2.1 Монотонность функции. Промежутки возрастания и убывания, 3.2.5 Точки экстремума функции, 3.2.6 Наибольшее и наименьшее значения функции

Функция определена на промежутке На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция принимает наибольшее значение.

Решение. Cмена знака производной с положительного на отрицательный соответствует точке максимума, следовательно, в точке с абсциссой −2 достигается наибольшее значение функции.

 Ответ: −2.

10.

На рисунке изображён график функции Найдите количество точек максимума функции принадлежащих интервалу (−4; 7).

 

Решение. Точки максимума соответствуют точкам, в которых функция перестаёт возрастать и начинает убывать. На интервале (−4; 7) функция имеет четыре точки максимума.

 

Ответ: 4.

Ответ: 4

523369

4

Кодификатор ФИПИ/Решу ЕГЭ: 4.2.1 Применение производной к исследованию функций и построению графиков

11.

На рисунке изображён график функции Найдите количество точек минимума функции принадлежащих интервалу (−4; 7).

Решение. Точки минимума соответствуют точкам, в которых функция перестаёт убывать и начинает возрастать. На интервале (−4; 7) функция имеет пять точек минимума.

 Ответ: 5.

Ответ: 5

523394

5

Кодификатор ФИПИ/Решу ЕГЭ: 4.2.1 Применение производной к исследованию функций и построению графиков

12.

 

 

На рисунке изображён график функции   — производной функции определенной на интервале (−5; 5). Найдите точку минимума функции

Решение. Точке минимума соответствует изменение знака производной с минуса на плюс. Поэтому

 Ответ: 4.

Решение. Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак, то это точка экстремума. На отрезке [–2; 6] график производной пересекает ось абсцисс, производная меняет знак с плюса на минус. Следовательно, точка 4 является точкой экстремума.

 

Ответ: 4.

Ответ: 4

27502

4

13.

На рисунке изображен график функции f(x), определенной на интервале (−5; 5). Найдите количество точек, в которых производная функции f(x) равна 0.

Ответ: 4.

Решение. Точки минимума дифференцируемой функции соответствуют изменению знака её производной с минуса на плюс. На отрезке [−4; 8] лежат две такие точки: 2 и 7.

 

 

Ответ:2.

Ответ: 2

500910

2

Решение. Точки минимума соответствуют точкам смены знака производной с отрицательного на положительный. На интервале (1; 10) функция имеет одну точку минимума x = 9.

 

Ответ: 9.

Ответ: 9

501188

9

14

На рисунке изображён график производной y = f'(x) функции y = f(x), определённой на интервале (−4; 8). В какой точке отрезка [−3; 1] функция y = f(x) принимает наименьшее значение?

 

Ответ: 1.

 

Решение. На заданном отрезке производная функции отрицательна, поэтому функция на этом отрезке убывает. Поэтому наименьшее значение функции достигается на правой границе отрезка, т. е. в точке

 

Ответ: 1.

Ответ: 1

504233

1

Раздел: Математический анализ

 

 

 

 

 

 

 

 

 

 

 

Решить самостоятельно.

1.      Найти критические точки функции f(x) = -2x³ +6x² + 48x - 16 (в ответ записать меньшее значение).  

 

2.      Исследовать функцию f(x) =x³ - 27x + 20 на экстремумы ( без таблицы, в ответ записать а) точку минимума; б) минимум функции).  

 

 

3.       Исследовать функцию f(x) =3x⁴ - 4x³ + 5 на экстремумы ( сделать таблицу, в ответ записать  а) наименьшую критическую точку; б) точку экстремума; в) экстремум функции; г) что происходит с функцией в критической точке х=0 ?).  

4.       13.  На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x),.

 

 

 

 

5.

На рисунке изображен график производной функции f(x), определенной на интервале (−18; 6). Найдите количество точек минимума функции f(x) на отрезке [−13;1].

6.     

На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

7.       На рисунке изображен график производной функции f(x), определенной на интервале (−7; 14). Найдите количество точек максимума функции f(x) на отрезке [−6; 9].

8.        

9.Решение. Точки максимума соответствуют точкам смены знака производной с положительного на отрицательный. На отрезке [−6; 9] функция имеет одну точку максимума x = 7.

10. 

11.Ответ: 1.

12.Ответ: 1

13.27494

14.1

8.На рисунке изображен график производной функции определенной на интервале Найдите количество точек минимума функции на отрезке

8.        

9.На рисунке изображен график производной функции f(x), определенной на интервале (−11; 11). Найдите количество точек экстремума функции f(x) на отрезке [−10; 10].

 

 

10.

На рисунке изображен график производной функции f(x), определенной на интервале (−4; 8). Найдите точку экстремума функции f(x) на отрезке [−2; 6].

 11.  На рисунке изображён график производной функции определенной на интервале (−8; 9). Найдите количество точек минимума функции принадлежащих отрезку

[−4; 8].

12.  

На рисунке изображён график функции у = f'(x) — производной функции f(x) определённой на интервале (1; 10). Найдите точку минимума функции f(x).

13.

Функция y = f (x) определена и непрерывна на отрезке [−5; 5]. На рисунке изображён график её производной. Найдите точку x₀, в которой функция принимает наименьшее значение, если  f (−5) ≥ f (5).

14.

На рисунке изображен график функции — производной функции f(x), определенной на интервале (−10; 6). В какой точке отрезка [−2; 4] функция f(x) принимает наименьшее значение?

 

Решение. Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак с минуса на плюс, то это точка минимума. На отрезке [–2; 4] график производной пересекает ось абсцисс в точке 3 и в этой точке производная меняет знак с минуса на плюс. Следовательно, точка 3 является точкой минимума на данном отрезке.

 

Ответ: 3.

Ответ: 3

505442

3

Источник: ЕГЭ по математике 05.06.2014. Основная волна. Запад. Вариант 1.

15.

Функция y = f(x) определена на промежутке (−6; 4). На рисунке изображен график ее производной. Найдите абсциссу точки, в которой функция y = f(x) принимает наибольшее значение.

 

Решение. Cмена знака производной с положительного на отрицательный соответствует точке максимума, следовательно, в точке с абсциссой −2 достигается наибольшее значение функции.

 

Ответ: −2.

Ответ: -2

509035

-2

Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 1.

16.

На рисунке изображен график производной функции y = f(x). При каком значении x эта функция принимает свое наибольшее значение на отрезке [−4; −2]?

 

 

 

 

 

 

 

 

 

 

 

 

Ответы на самостоятельную работу.

1.        -2

2.        а) -3;   б) 14

3.        а) 0;   б) 1;  в) 4;  г) х=0 – точка перегиба.

4.        44

5.         1

6.         5

7.         1

8.         1

9.         5

10.                  4

11.                  2

12.                  0

13.                  3

14.                  3

15.                  -2

16.                  -4

 

 

Скачано с www.znanio.ru