Исследовательский проект на тему "Фракталы"

Окружная научная конференция молодых исследователей «Шаг в будущее»

Муниципальный этап

Ханты-Мансийский автономный округ - Югра

Муниципальное автономное общеобразовательное учреждение

          «Средняя общеобразовательная школа №4»

Фракталы

(исследовательский проект по информатике)

                                                                                                            Автор:

Г…. Т…… Е……,

ученик 10 класса

Руководитель проекта:

Гудкова Елена Павловна,

учитель информатики

г. Мегион

2023 год

I. Аннотация

В сети Интернет я посмотрел видеоролик с различными красивыми фигурами – фракталами. Он меня сильно впечатлил,  и я захотел глубже изучить эту тему. Познакомился с другими видеороликами о фракталах. Изучал информацию, читал различные статьи. Я занимаюсь решением задач на программирование, это олимпиадное программирование. У меня возникло желание попробовать самому создать программу генерирующую фрактал, сгенерировать построение этих красивых изображений, в которых прослеживается повторение фрагментов. Так и появилась цель моего проекта.

Цель проекта: Выяснить, что такое фракталы, их виды и применение. Создать несколько программ генерирующих различные фракталы. Я выбрал создание трех фракталов:

·         треугольник Серпинского;

·         множество Мандельброта;

·         множество Жюлиа.

Задачи:

·         собрать информацию о фракталах, первые их упоминания;

·         изучить, проанализировать, систематизировать информацию;

·         изучить различные модули языка Рython, которые мне понадобятся для работы с графикой и математикой фракталов;

·         создать программу на языке программирования Python.

Методы исследования: Теоретические (изучение, анализ, моделирование, обобщение данных), эмпирические (эксперимент, испытания).

Проектный продукт: создание программ генерирующих фракталы.

Вывод: В результате исследования я  проанализировал историю развития фракталов, познакомился с их видами и сферами применения, создал программы генерирующие фракталы. Работая над этой темой, я понял, что фракталы – это обширное направление, которое находит много применений в жизни. Для меня это был интересный опыт создания компьютерной графики с помощью языка программирования Python. Работая над созданием программного кода изучил математические основы построения одного из видов компьютерной графики – фракталов.

План проектной работы

Проблема: Новая форма искусства переопределяет границы между «изобретением» и «открытием», как они понимаются в науках, и «творчеством», как они понимаются в пластических искусствах. Может ли чистая геометрия восприниматься «человеком с улицы» как нечто прекрасное? Или более конкретно, может ли форма, которая задается простым уравнением или правилом построения, восприниматься людьми, далекими от геометрии, как эстетически ценная – то есть, по крайней мере, как удивительно декоративная – или даже как произведение искусства? Если геометрическая форма – фрактал, то ответ – да. Что такое фракталы? Можно ли их построить с помощью языка программирования?

Задачи: Собрать, изучить, проанализировать, систематизировать информацию о фракталах. Изучить различные модули языка Python, которые мне понадобятся для работы с графикой и построением математической модели фракталов. Создать программу на языке программирования Python, которая выполняет построение фракталов.

1. Теоретическая часть:

Что такое фрактал?

  Фракталы вокруг нас повсюду, и в очертаниях гор, и в изгибистой линии морского берега. Это и папоротники, крона деревьев. Некоторые из фракталов постоянно меняются, похоже передвигающимся облакам или мерцающему пламени, в то время как другие, похоже деревьям или нашим сосудистым системам, берегут структуру, полученную в процессе эволюции. Очень часто мы встречаемся с особыми объектами, только мало кто знает, что это и есть фракталы. Фракталы — уникальные объекты, порожденные непонятными ходом беспорядочного мира. Они встречаются как в небольших объектах, например, клеточная мембрана, и огромных, таких как Солнечная система и галактика.

Первые упоминания фракталов

Само слово «фрактал» появилось благодаря гениальному ученому Бенуа Мандельброту. Он сам придумал этот термин в семидесятых годах прошлого века, позаимствовав слово «fractus» из латыни, где оно буквально означает «ломанный» или «дробленный». Что же это такое? Сегодня под словом «фрактал» чаще всего принято подразумевать графическое изображение структуры, которая в более крупном масштабе подобна сама себе. Математическая база для появления теории фракталов была заложена за много лет до рождения Бенуа Мандельброта, однако развиться она смогла лишь с появлением вычислительных устройств. В начале своей научной деятельности Бенуа работал в исследовательском центре компании IBM. В то время сотрудники центра трудились над передачей данных на расстояние. В ходе исследований ученые столкнулись с проблемой больших потерь, возникающих из-за шумовых помех. Перед Бенуа стояла сложная и очень важная задача — понять, как предсказать возникновение шумовых помех в электронных схемах, когда статистический метод оказывается неэффективным.

Просматривая результаты измерений шума, Мандельброт обратил внимание на одну странную закономерность — графики шумов в разном масштабе выглядели одинаково. Идентичная картина наблюдалась независимо от того, был ли это график шумов за один день, неделю или час. Стоило изменить масштаб графика, и картина каждый раз повторялась.

При жизни Бенуа Мандельброт неоднократно говорил, что он не занимается формулами, а просто играет с картинками. Этот человек мыслил очень образно, а любую алгебраическую задачу переводил в область геометрии, где, по его словам, правильный ответ всегда очевиден.

Неудивительно, что именно человек с таким богатым пространственным воображением стал отцом фрактальной геометрии. Ведь осознание сути фракталов приходит именно тогда, когда начинаешь изучать рисунки и вдумываться в смысл странных узоров-завихрений.

Фрактальный рисунок не имеет идентичных элементов, но обладает подобностью в любом масштабе. Построить такое изображение с высокой степенью детализации вручную ранее было просто невозможно, на это требовалось огромное количество вычислений. Например, французский математик Пьер Жозе Луи Фату описал это множество более чем за семьдесят лет до открытия Бенуа Мандельбротом. Если же говорить про принципы самоподобия, то о них упоминалось еще в трудах Лейбница и Георга Кантора. Один из первых рисунков фрактала был графической интерпретацией множества Мандельброта, которое родилось благодаря исследованиям Гастона Мориса Жюлиа.

Этот французский математик задался вопросом, как будет выглядеть множество, если построить его на основе простой формулы, проитерированной циклом обратной связи. Если объяснить «на пальцах», это означает, что для конкретного числа мы находим по формуле новое значение, после чего подставляем его снова в формулу и получаем еще одно значение. Результат — большая последовательность чисел.

Чтобы получить полное представление о таком множестве, нужно проделать огромное количество вычислений — сотни, тысячи, миллионы. Вручную это сделать было просто нереально. Но когда в распоряжении математиков появились мощные вычислительные устройства, они смогли по-новому взглянуть на формулы и выражения, которые давно вызывали интерес. Мандельброт был первым, кто использовал компьютер для просчета классического фрактала. Обработав последовательность, состоящую из большого количества значений, Бенуа перенес результаты на график. Вот что он получил.

Впоследствии это изображение было раскрашено (например, один из способов окрашивания цветом — по числу итераций) и стало одним из самых популярных изображений, какие только были созданы человеком.

Как гласит древнее изречение, приписываемое Гераклиту Эфесскому, «В одну и ту же реку нельзя войти дважды». Оно как нельзя лучше подходит для трактования геометрии фракталов. Как бы детально мы ни рассматривали фрактальное изображение, мы все время будем видеть схожий рисунок.

Практическое применение фракталов

Теория фракталов скоро нашла практическое применение. Поскольку она тесно связана с визуализацией самоподобных образов, неудивительно, что первыми, кто взял на вооружение алгоритмы и принципы построения необычных форм, были художники.

Будущий сооснователь легендарной студии Pixar - Лорен Карпентер в 1967 году начал работать в компании Boeing Computer Services, которая была одним из подразделений известной корпорации, занимающейся разработкой новых самолетов. В 1977 году он создавал презентации с прототипами летающих моделей. В обязанности Лорена входила разработка изображений проектируемых самолетов. Он должен был создавать картинки новых моделей, показывая будущие самолеты с разных сторон. В какой-то момент в голову будущему основателю Pixar Animation Studios пришла в голову креативная идея использовать в качестве фона изображение гор. Сегодня такую задачу может решить любой школьник, но в конце семидесятых годов прошлого века компьютеры не могли справиться со столь сложными вычислениями — графических редакторов не было, не говоря уже о приложениях для трехмерной графики. В 1978 году Лорен случайно увидел в магазине книгу Бенуа Мандельброта «Фракталы: форма, случайность и размерность». В этой книге его внимание привлекло то, что Бенуа приводил массу примеров фрактальных форм в реальной жизни и доказывал, что их можно описать математическим выражением.

Такая аналогия была выбрана математиком не случайно. Дело в том, что как только он обнародовал свои исследования, ему пришлось столкнуться с целым шквалом критики. Главное, в чем упрекали его коллеги, — бесполезность разрабатываемой теории. «Да, — говорили они, — это красивые картинки, но не более. Практической ценности теория фракталов не имеет». Были также те, кто вообще считал, что фрактальные узоры — просто побочный результат работы «дьявольских машин», которые в конце семидесятых многим казались чем-то слишком сложным и неизученным, чтобы всецело им доверять. Мандельброт пытался найти очевидное применение теории фракталов, но, по большому счету, ему и не нужно было это делать. Последователи Бенуа Мандельброта в следующие 25 лет доказали огромную пользу от подобного «математического курьеза», и Лорен Карпентер был одним из первых, кто опробовал метод фракталов на практике.

Проштудировав книжку, будущий аниматор серьезно изучил принципы фрактальной геометрии и стал искать способ реализовать ее в компьютерной графике. Всего за три дня работы Лорен смог визуализировать реалистичное изображение горной системы на своем компьютере. Иными словами, он с помощью формул нарисовал вполне узнаваемый горный пейзаж.

Принцип, который использовал Лорен для достижения цели, был очень прост. Он состоял в том, чтобы разделять более крупную геометрическую фигуру на мелкие элементы, а те, в свою очередь, делить на аналогичные фигуры меньшего размера

Используя более крупные треугольники, Карпентер дробил их на четыре мелких и затем повторял эту процедуру снова и снова, пока у него не получался реалистичный горный ландшафт. Таким образом, ему удалось стать первым художником, применившим в компьютерной графике фрактальный алгоритм для построения изображений. Как только стало известно о проделанной работе, энтузиасты по всему миру подхватили эту идею и стали использовать фрактальный алгоритм для имитации реалистичных природных форм.

В настоящее время все популярные приложения для создания трехмерных ландшафтов используют аналогичный принцип генерирования природных объектов. Terragen, Bryce, Vue и прочие трехмерные редакторы полагаются на фрактальный алгоритм моделирования поверхностей и текстур.

Виды фракталов:

1.      геометрические;

2.      алгебраические;

3.      стохастические.

Геометрические виды фракталов являются самыми наглядными и простыми в строении. Увидеть их может любой человек. Множество таких фракталов можно нарисовать на обычном листке бумаги в клетку. Примером являются: треугольник Серпинского, снежинка Коха, кривая дракона, дерево Пифагора. «Снежинка Коха» стала основой фрактальных антенн, которые мы используем в мобильных устройствах. Благодаря такой форме антенны имеют компактный размер с широким диапазоном действия.

Алгебраические фракталы. Это самая крупная группа фракталов, которая базируется на основе разных алгебраических формул. Ярким примером является фрактал Мандельброта. В настоящее время их принято отображать в цвете. Получаются красивейшие необычные орнаменты.

Стохастические фракталы. Строятся путём хаотического изменения некоторых параметров. При этом получаются объекты, очень похожие на природные. Фракталы данного вида широко применяются в киноиндустрии. С помощью компьютерной графики создаются искусственные горы, облака, поверхности моря, планеты, береговые линии, несимметричные деревья.

Практическая часть

Я создал три программы на языке Python. Они будут генерировать треугольник Серпинского, множество Мандельброта и множество Жулиа. Приведу словесное описание алгоритмов работы моих программ.

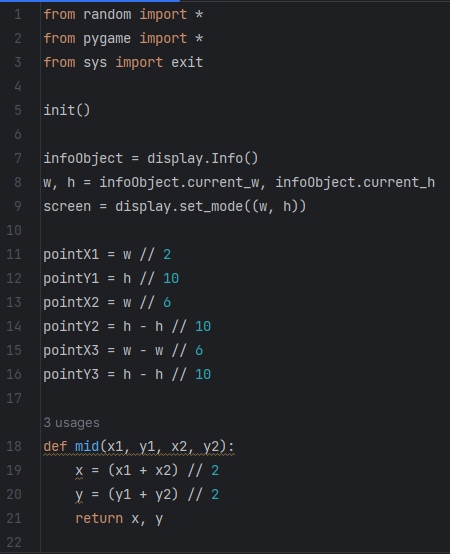
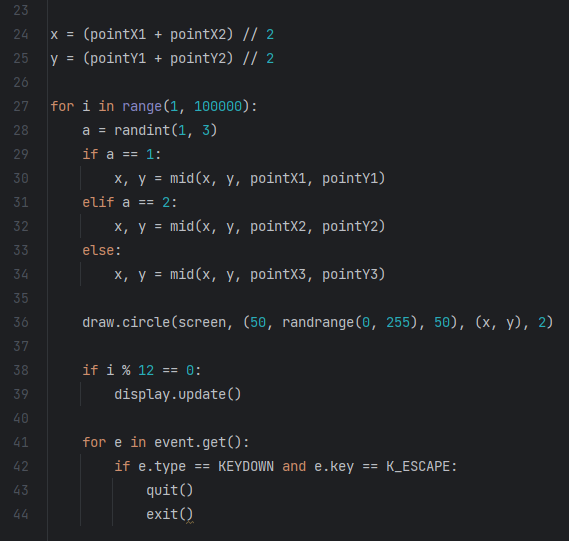
Первая программа. Генерирует треугольник Серпинского. Делает она это следующим образом. Сначала мы обозначаем вершины треугольника. Далее отмечаем середину одной из его сторон. Теперь случайным образом мы отстраиваем точку лежащую посередине точки, которую мы только что отметили и любой из сторон. Так мы делаем много раз. Получается Треугольник Серпинского. (Приложение 3)

Вторая программа. Множество Мандельброта и множество Жюлиа мы строим при помощи комплексных чисел. Это числа вида a + b * i, {\displaystyle a+bi,}  где {\displaystyle a,b}a и  b — вещественные числа, {\displaystyle i}i — мнимая единица, то есть число, для которого выполняется равенство: {\displaystyle i^{2}=-1.}I² = -1

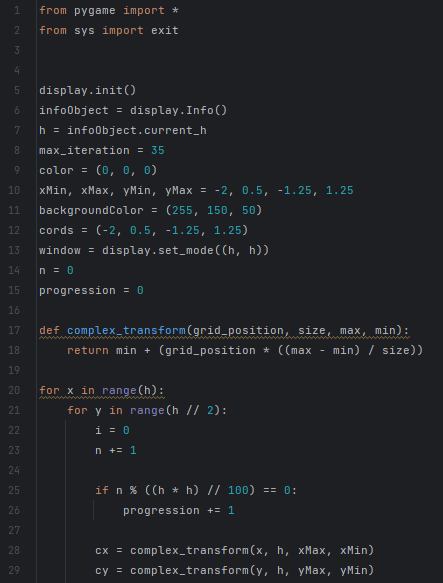
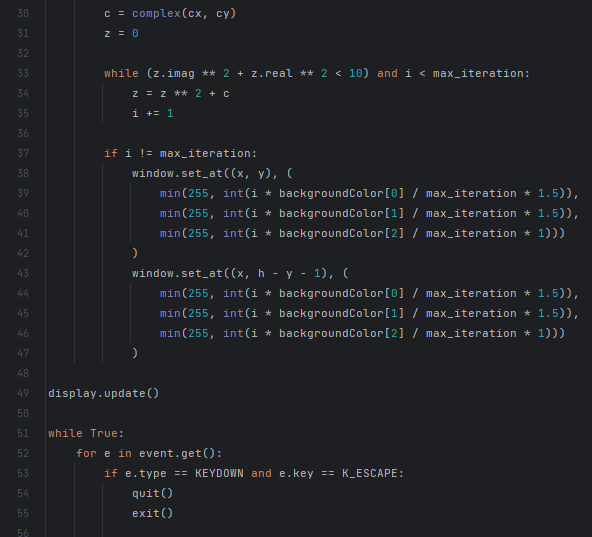
  Для множества Мандельброта применяется формула f(z) = z² + c, где с комплексное число. Всё множество полностью расположено внутри круга радиуса 2 на плоскости. Поэтому будем считать, что если для точки c последовательность итераций функции f(z) = z² + c, с сначальным значением z = 0 после некоторого большого их числа N (скажем, 100) не вышла за пределы этого круга, то точка принадлежит множеству и красится в черный цвет. Соответственно, если на каком-то этапе, меньшем N, элемент последовательности по модулю стал больше 2, то точка множеству не принадлежит и остается белой. Таким образом, можно получить черно-белое изображение множества, которое и было получено Мандельбротом. Чтобы сделать его цветным, можно, например, каждую точку не из множества красить в цвет, соответствующий номеру итерации, на котором её последовательность вышла за пределы круга. (Приложение 2, Приложение 5)

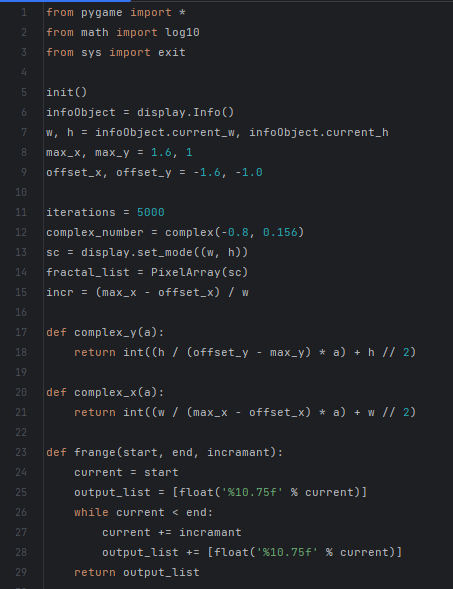
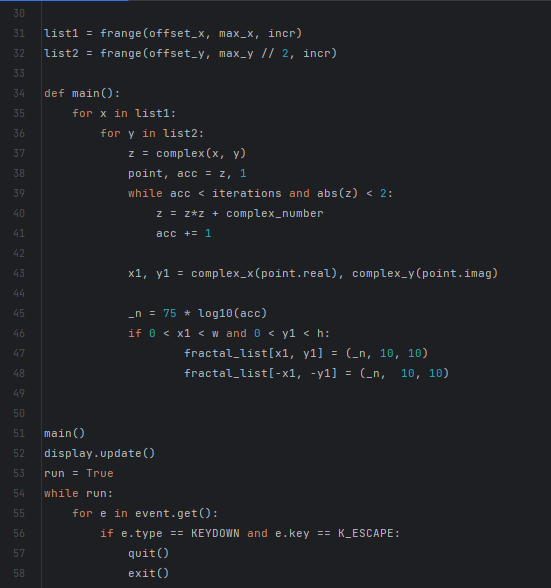
Третья программа. Для множества Жюлиа мы сканируем множество точек на комплексной плоскости, например, в диапазоне [-2; 2] по мнимой и действительной осям. Каждая точка – это комплексное число. Наша задача определить, относится ли эта точка к множеству Жюлиа или нет. Для этого, мы делаем n итераций для той же функции, что и для множества Мандельброта. Если окажется, что после n итераций модуль полученного комплексного числа меньше двух, то такую точку следует отнести к множеству Жюлиа, иначе, это точка фона. (Приложение 1, Приложение 4) Аналогично множеству Мандельброта точки фона можно окрасить.

В результате выполненной практической работы:

·            Создана программа генерирующая треугольник Серпинского.

·            Создана программа генерирующая множество Мандельброта.

·            Создана программа генерирующая множество Жюлиа.

·            Создана презентация в программе PowerPoint, в которой я показываю фото полученных фракталов. А также краткую информацию о каждом важном моменте проекта.

Заключение

Цель моего проекта: создать программы генерирующие треугольник Серпинского, множество Мандельброта и множество Жюлиа. Работа над проектом показала, что я достиг цели и выполнил все задачи. Мною были найдены ответы на поставленные вопросы.

Выводы. Проанализировав изученную информацию, я получил ответы на многие свои вопросы.

· Фрактальная математика ещё молодое направление в науке. Математические фракталы активно используются в нанотехнологиях, у трейдеров, экономистов. Они помогают анализировать курс фондовых бирж, торгового рынка.

· Есть три основных вида фракталов.

· Фракталы это не только красивые картинки, они находят много практических применений. Фрактальные элементы в сакральной геометрии, по мнению философов, призваны гармонизировать энергии тела и помочь в практике исцеления. Область нефтехимии – для создания пористых материалов, а в биологии для развития популяций, генной инженерии. В IT-сфере передовые 3D иллюстрации, децентрализованные сети, фрактальное сжатие информации для IP-адресов. В радиоэлектронике выпускают антенны, имеющие фрактальную форму. Ученые создали квантовый фрактал с помощью сканирующего туннельного микроскопа (STM) проводят исследования в области теории квантового сознания. В лабораторных условиях создают фрактальные структуры из квантовых частиц и измеряют их состояния и движения.

· Создавая программный код, изучил математические основы построения фрактальной графики. Для меня это был интересный опыт создания компьютерной графики с помощью языка программирования Python.

· Хочу продолжить работу над этим проектом. Создам сайт, на котором пользователи смогут моделировать фракталы в реальном времени, изменяя различные параметры изображения. Организую на сайте общую галерею фракталов, сгенерированных всеми пользователями. В наши дни теория фракталов находит широкое применение в различных областях человеческой деятельности, потому буду отражать эту информацию на страницах  своего сайта.

III. Список используемой литературы

https://3dnews.ru/754657

https://allatravesti.com/chto-takoe-fraktaly-mir-vokrug-nas-chast-1

https://waksoft.susu.ru/2019/04/27/mnozhestvo-mandelbrota-na-python/

https://proproprogs.ru/fractals/fractals-kak-postroit-mnozhestva-zhyulia

Приложение 1

Программный код  «Множество Жюлиа»

Приложение 2

Программный код  «Множество Мандельброта»

Приложение 3

Программный код  «Треугольник Серпинского»

Приложение 4

Сгенерированные фракталы «Множество Жюлиа»

Приложение 5

Сгенерированные фракталы «Множество Мандельброта»

Скачано с www.znanio.ru