Итоговая контрольная работа по геометрии, 9 класс

Итоговая контрольная работа  по геометрии (9 класс)

Вариант1

1. 

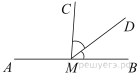
На прямой AB взята точка M. Луч MD — биссектриса угла CMB. Известно, что ∠DMC = 41°. Найдите угол CMA. Ответ дайте в градусах.

2. 

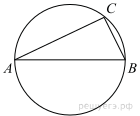
Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Найдите угол ABC, если угол BAC равен 30°. Ответ дайте в градусах.

3. 

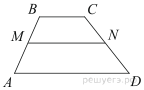
В трапеции ABCD известно, что AD = 7, BC = 5, а её площадь равна 72. Найдите площадь трапеции BCNM, где MN – средняя линия трапеции ABCD.

4. 

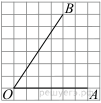
Найдите тангенс угла , изображённого на рисунке.

5. 

Какое из следующих утверждений верно?

1) Сумма углов выпуклого четырёхугольника равна 360 градусам.

2) Средняя линия трапеции равна сумме её оснований.

3) Любой параллелограмм можно вписать в окружность.

6. Основания трапеции равны 16 и 34. Найдите отрезок, соединяющий середины диагоналей трапеции.

7. В остроугольном треугольнике ABC проведены высоты  и  Докажите, что углы  и  равны.

8.  Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC.

Вариант2

1. 

В треугольнике  известно, что ,  — биссектриса. Найдите угол . Ответ дайте в градусах.

2. 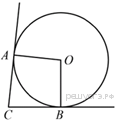В угол C величиной 57° вписана окружность, которая касается сторон угла в точках A и B, точка O - центр окружности. Найдите угол AOB. Ответ дайте в градусах.

3. 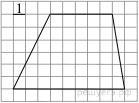Найдите площадь трапеции, изображённой на рисунке.

4. 

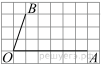
Найдите тангенс угла , изображённого на рисунке.

5. Какое из следующих утверждений верно?

1) Диагонали параллелограмма равны.

2) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне.

3) Если две стороны и угол одного треугольника равны соответственно двум сторонам и углу другого треугольника, то такие треугольники равны.

 Если утверждений несколько, запишите их номера в порядке возрастания.

6. 

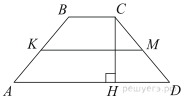
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.

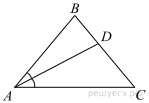
7. 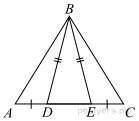На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что отрезки BD и BE тоже равны. Докажите, что треугольник АВС — равнобедренный.

8. Три окружности, радиусы которых равны 2, 3 и 10, попарно касаются внешним образом. Найдите радиус окружности, вписанной в треугольник, вершинами которого являются центры этих трёх окружностей.