
Изменение кинетической энергии тела в среде с постоянной энергией. Эффект Аристотеля-Мпембы
Change in kinetic energy in the environment with constant energy
Штром
Виктор Фёдорович, инженер - программист, Санкт-Петербург, Россия
vfnv@mail.ru
Аннотация: Разработан алгоритм расчёта и программы кинетической энергии тела, состоящего из упругих шаров, в среде с постоянной энергией. Написана компьютерная программа. Проведены физические эксперименты на остывание тел в воздушной среде с постоянной температурой. Показано качественное совпадение графиков программы и экспериментов.
Ключевые слова: кинетическая энергия; алгоритм; эксперимент.
Abstract: The algorithm of change in kinetic energy of the body consisting of elastic spheres in the environment with constant energy is received. The software application is written. Physical experiments on the cooling of bodies in the constant temperature air are made. Qualitative coincidence of calculated and experimental data is shown.
Keywords: kinetic energy; algorithm; experiment.
УДК 536-3
Ведение
В конце 17 века Исаак Ньютон изучал охлаждение тел. Эксперименты показали, что скорость охлаждения примерно пропорциональна разнице температур между нагретым телом и окружающей средой. Этот факт можно записать в виде дифференциального уравнения:
![]() , (1)
, (1)
где Q − количество теплоты, A − площадь поверхности тела, через которую передается тепло, T − температура тела, TS − температура окружающей среды, α − коэффициент теплопередачи, зависящий от геометрии тела, состояния поверхности, режима теплопередачи и других факторов.
Как видно из формулы (1), в коэффициенте теплопередачи заложено много неопределённых факторов. Если такие факторы, как геометрия тела, состояние поверхности, режим теплопередачи указаны и их можно измерить, то такие факторы как частота колебания молекул в твёрдых и жидких веществах, или скорость молекул в газах не указаны, т.к. в 17 веке ещё не были известны молекулярно кинетические свойства вещества.
Молекулярно-кинетическая теория (сокращённо МКТ) — теория, возникшая в XIX веке и рассматривающая строение вещества, в основном газов, с точки зрения трёх основных приближенно верных положений:
1. все тела состоят из частиц: атомов, молекул и ионов;
2. частицы находятся в непрерывном хаотичном движении (Тепловом);
3. частицы взаимодействуют друг с другом путём абсолютно упругих столкновений.
Недостаточность кинетической теории материи, господствовавшей в 19 веке первым отметил Николай Николаевич Пирогов. Он показал, что установленный английским физиком Максвеллом закон распределения скоростей молекул газа в их хаотическом движении (помогающий вычислить, какая доля молекул обладает той или иной скоростью) действителен лишь в том случае, когда газ занимает бесконечно большой объем. Для того чтобы правильно отобразить распределение скоростей молекул в газе, занимающем определенный конечный объем, показал Пирогов, надо принять в расчет и действие стенок сосуда на молекулы газа, стремящееся выровнять, упорядочить это движение..... [1,2,3].
В. Томпсоном (William Thomson) была поставлена и решена задача об остывании полупространства. " Пусть однородная среда заполняет полупространство, ограниченное плоскостью х - 0. В начальный момент времени t = 0 температура среды всюду одинакова и равна Т0. Температура на поверхности среды всё время поддерживается постоянной и равнаТ1 ≠ Т0. ..... " [4]. Дальше предполагается, что в начальный момент на границе среды температура испытывает скачок. Затем задача формализуется дифференциальным уравнением и решается.
1. Модель обмена кинетической энергией тела, состоящего из абсолютно упругих частиц с окружающей средой.
Рассмотрим эту задачу с позиции МКТ, учитывая высказывание Н. Н. Пирогова о взаимодействии молекул исходного вещества с молекулами окружающей среды.
Как известно тепло передаётся тремя способами: 1) кинетически, 2) конвекцией, 3) излучением. Чтобы исключить конвекцию, будем считать, что исследуемое тело состоит из твёрдого вещества или из покоящейся жидкости. Ввиду незначительности влияния излучения в эксперименте не будем учитывать и излучение. Также положим, что между молекулами происходят упругие столкновения.
После всех приведённых ограничений сформулируем следующую задачу.
Поместим на плоскость один слой абсолютно упругих шаров (b). Получим двумерную задачу. Шары имеют одинаковую постоянную частоту колебания vb. Выделим в плоскости прямоугольник, заполненный абсолютно упругими шарами (r) с начальной частотой колебания vr0 > vb. Левая сторона открыта и граничит с окружающей средой. Три других стороны являются абсолютно твёрдые стенки. Массы всех шаров равны. Таблица. 1.
В каждый момент происходит равновероятное колебание в одну из четырёх сторон, происходит обмен импульсами. Так как нулевой столбец принадлежит окружающей среде, то его частота колебания восстанавливается. Шары внутри прямоугольника получают частоту колебания vr0 или vb.
Найти время выравнивания частот колебания шаров внутри прямоугольник с окружающей средой.
|
0 |
1 |
2 |
3 |
. |
n |
|
|
|
|
j |
|
. |
|
|
|
b |
r |
r |
r |
. |
r |
|
|
b |
r |
r |
r |
. |
r |
|
|
b |
r |
r |
r |
. |
r |
|
|
b |
r |
r |
r |
. |
r |
i |
|
b |
r |
r |
r |
. |
r |
|
|
b |
r |
r |
r |
. |
r |
|
|
b |
r |
r |
r |
. |
r |
|
|
b |
r |
r |
r |
. |
r |
|
|
b |
r |
r |
r |
. |
r |
|
|
|
|
|
|
. |
|
|
Таблица 1
Решение.
Рассмотрим варианты обмена импульсами в поставленной задаче. каждый шар с вероятностью 1/4 ударится в одну из четырёх сторон. Предполагается, что колебание стенок << колебания внутренней части прямоугольника. Это даёт возможность считать всегда встречным удар внутренних шаров со стенками. При ударе в верхнюю и нижнюю сторону происходит обмен импульсами между молекулами тела. При ударе в верхнюю и нижнюю стенку прямоугольника происходит упругий отскок. Отсюда следует, что сумма импульсов в столбце не изменится, не теряя общности решения представим прямоугольник в задаче в виде одного ряда шаров, таблица 2.
|
0 |
1 |
2 |
3 |
. |
n |
|
|
|
|
j |
|
. |
|
|
|
b |
r |
r |
r |
. |
r |
|
|
|
|
|
Таблица 2
Время будем измерять тактами (шагами) цикла компьютерной программы.
Методом индукции получим алгоритм вычисления числа
тактов вероятности существования начального импульса ![]() шарика со скоростью vr
в j
столбце
на i такте. i
= 0, 1, 2, ...
шарика со скоростью vr
в j
столбце
на i такте. i
= 0, 1, 2, ...
Задача 1. ![]()
|
0 |
1 |
2 |
|
|
|
|
|
b |
r |
|
|
|
|
|
Таблица 3
![]()
![]()
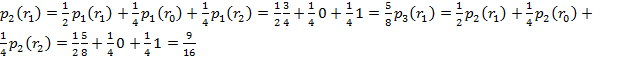
Задача 2. ![]()
|
0 |
1 |
2 |
3 |
|
|
|
|
|
|
b |
r |
r |
|
|
|
|
|
|
Таблица 4
![]()
![]()
![]()
![]()
Задача 3. ![]()
![]()
![]() (2)
(2)
Задача 4. В задачах 1-3 была вычислена вероятность столкновения соседних шаров в зависимости от направления удара и не учитывалась скорость (частота) столкновения. Это значит, что в каждом такте формулы (2) вероятность будет уменьшаться на определённую величину, пропорциональную частоте столкновений с шарами меньшей кинетической энергии.
Введём частоту (скорость) в формулу (2).
![]() ,
,
где 1 > s
>
0 - коэффициент влияния скорости на вероятность,![]() - новая вероятность.
- новая вероятность.
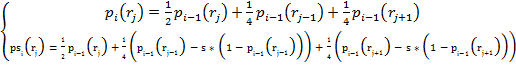 (3)
(3)
![]()
По алгоритму (3) написана компьютерная программа для двух одинаковых тел, состоящих из упругих шаров, с разной начальной скоростью, в одной и той же окружающей среде. Файл с исполняемой программой [6].
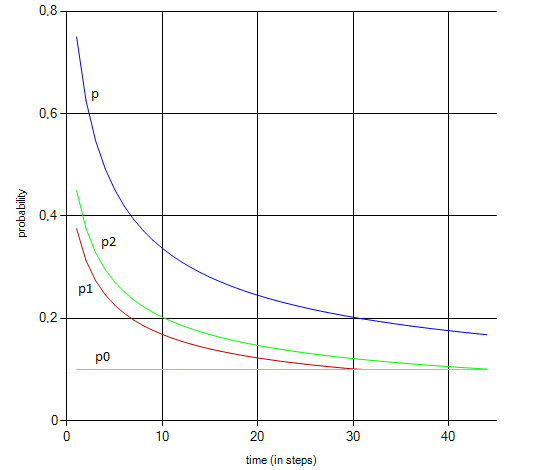
p0 - вероятность начального импульса шаров окружающей среды.
p - вероятности импульса заданного шара (здесь первый слева).
p1 - вероятности импульса заданного шара (здесь первый слева), с учётом частоты колебания s1.
p2 - вероятность импульса заданного шара (здесь первый слева), с учётом частоты колебания s1.
s1 > s2.
Рис. 1
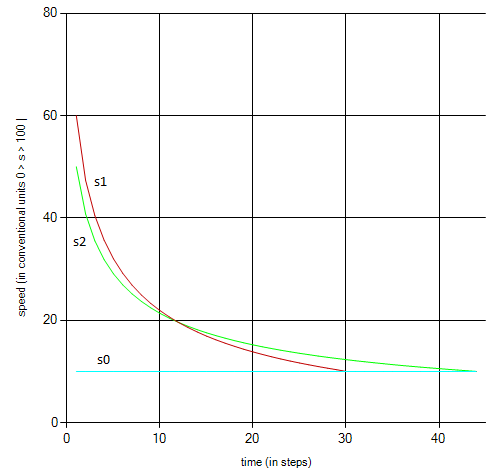
s0 - условная начальная скорость шаров окружающей среды..
s1 - скорость заданного шара.
s2 - скорость заданного.
s1 > s2.
Рис. 2
Из графиков 1, 2 видим, что чем больше начальная скорость шаров, тем быстрее происходит выравнивание скорости шаров внутри прямоугольника со скоростями шаров окружающей среды.
Из МКТ следует пропорциональность температуры и интенсивности движения молекул.
2. Физические эксперименты по условиям алгоритма.
Эксперимент 1.
Два пластмасовых шарика (пинг-понг) диаметром 40 мм. Шарики заполнены водой объёмом 29 мл. В шариках просверлены отверстия для термодатчиков, Fig, 6. Температура воздуха ≈ -15,7°C . Интервал времени регистрации температуры 2 мин.
|
NN |
T1 |
T2 |
|
1 |
39,6 |
32 |
|
2 |
34,2 |
25,7 |
|
3 |
30,8 |
22,8 |
|
4 |
28,7 |
21,2 |
|
5 |
26,3 |
19,2 |
|
6 |
25 |
18,1 |
|
7 |
22,5 |
16,2 |
|
8 |
20,3 |
14,5 |
|
9 |
18,8 |
13,4 |
|
10 |
17,4 |
12,2 |
|
11 |
15,8 |
11 |
|
12 |
13,7 |
9,3 |
|
13 |
12,4 |
8,3 |
|
14 |
10,6 |
6,9 |
|
15 |
9 |
5,6 |
|
16 |
8,2 |
5 |
|
17 |
6,7 |
3,9 |
|
18 |
5,9 |
3,4 |
|
19 |
4,8 |
2,3 |
|
20 |
3,3 |
1,3 |
|
21 |
1,8 |
0,1 |
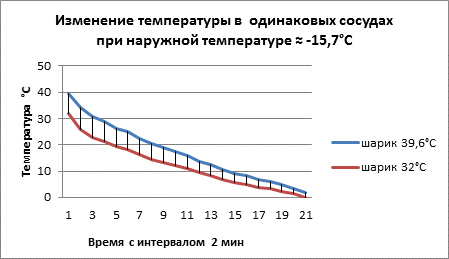
Рис. 3
Таблица 5
Эксперимент 2.
Повторяет эксперимент 1. Изменена температура окружающей среды -8°C. Интервал времени регистрации температуры 1мин.
|
1 |
47 |
42.8 |
|
2 |
43.6 |
39 |
|
3 |
40.3 |
35.9 |
|
4 |
36.6 |
32.7 |
|
5 |
33.3 |
29.9 |
|
6 |
30.3 |
27 |
|
7 |
27.9 |
24.7 |
|
8 |
25 |
21.6 |
|
9 |
22.7 |
19.8 |
|
10 |
20.7 |
18 |
|
11 |
18.6 |
16.2 |
|
12 |
16.7 |
14.5 |
|
13 |
14.7 |
12.6 |
|
14 |
12.9 |
11.1 |
|
15 |
11.4 |
9.7 |
|
16 |
9.9 |
8.3 |
|
17 |
8.4 |
7 |
|
18 |
7.1 |
5.9 |
|
19 |
5.9 |
4.8 |
|
20 |
4.8 |
3.8 |
|
21 |
3.2 |
1.6 |
|
22 |
2.3 |
0.4 |
|
23 |
1.4 |
-0.2 |
|
24 |
0.8 |
-0.3 |
|
25 |
0.2 |
-0.3 |
|
26 |
-0.5 |
-0.3 |
|
27 |
-1 |
-0.3 |
|
28 |
-1.5 |
-0.1 |
|
29 |
-2.7 |
-0.3 |
|
30 |
-2.6 |
-0.2 |
|
31 |
-3.1 |
-0.1 |
|
32 |
-3.5 |
-0.2 |
|
33 |
-0.2 |
-0.1 |
|
34 |
-0.2 |
-0.2 |
|
35 |
0.2 |
-0.2 |
|
36 |
0.2 |
-0.2 |
|
37 |
0.2 |
-0.2 |
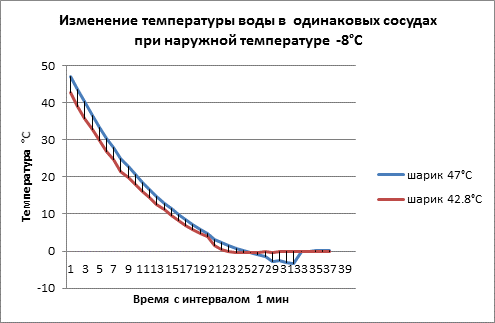
Рис. 4
Таблица 6
Вода имеет немонотонную зависимость температуры и плотности, поэтому необходимо учитывать жёсткость и форму сосуда. Вода переходит в лёд. Лёд имеет меньшую плотность. Пространство движения молекул воды ограничено размерами сосудов (пластмассовых шариков), что не позволяет монотонно продолжить обмен кинетической энергией между водой и окружающёй средой. Возрастает роль теплового излучения. Предложенный алгоритм учитывает только обмен кинетической энергией.
Эксперимент 3.
Два алюминиевых цилиндра диаметром 20 мм, высотой 40мм. В цилиндрах просверлены углубления 24мм. В углубления вставлены термодатчики, , Fig, 6. Температура воздуха ≈ -16,4°C . Интервал времени регистрации температуры 2 мин.
|
NN |
T1 |
T2 |
NN |
T1 |
T2 |
NN |
T1 |
T2 |
NN |
T1 |
T2 |
|
1 |
55,7 |
42,6 |
16 |
-8,5 |
-8,5 |
31 |
-14,2 |
-13,8 |
46 |
-16,4 |
-16 |
|
2 |
43,5 |
34 |
17 |
-9,6 |
-9,6 |
32 |
-14,2 |
-13,9 |
47 |
-16,5 |
-16 |
|
3 |
34,7 |
26,7 |
18 |
-10,5 |
-10,4 |
33 |
-14,2 |
-13,9 |
48 |
-16,5 |
-16 |
|
4 |
26,4 |
20,3 |
19 |
-11,2 |
-11 |
34 |
-14,2 |
-13,9 |
49 |
-16,5 |
-16 |
|
5 |
20,2 |
15,5 |
20 |
-11,9 |
-11,6 |
35 |
-14,3 |
-14 |
50 |
-16,5 |
-16 |
|
6 |
15,1 |
11,4 |
21 |
-12,3 |
-12,1 |
36 |
-14,5 |
-14,2 |
|
|
|
|
7 |
10,8 |
7,9 |
22 |
-12,8 |
-12,5 |
37 |
-14,8 |
-14,5 |
|
|
|
|
8 |
7 |
4,6 |
23 |
-13,2 |
-12,8 |
28 |
-15,2 |
-14,8 |
|
|
|
|
9 |
3,5 |
1,7 |
24 |
-13,4 |
-13,1 |
39 |
-15,4 |
-14,9 |
|
|
|
|
10 |
2,1 |
1 |
25 |
-13,6 |
-13,3 |
40 |
-15,8 |
-15,3 |
|
|
|
|
11 |
0,8 |
-0,6 |
26 |
-13,8 |
-13,5 |
41 |
-15,9 |
-15,5 |
|
|
|
|
12 |
-1,6 |
-2,7 |
27 |
-14 |
-13,6 |
42 |
-16,1 |
-15,6 |
|
|
|
|
13 |
-3,8 |
-4,6 |
28 |
-14,1 |
-13,7 |
43 |
-16,2 |
-15,8 |
|
|
|
|
14 |
-5,8 |
-6,2 |
29 |
-14,1 |
-13,8 |
44 |
-16,3 |
-15,9 |
|
|
|
|
15 |
-7,2 |
-7,4 |
30 |
-14,2 |
-13,8 |
45 |
-16,4 |
-15,9 |
|
|
|
Таблица 7
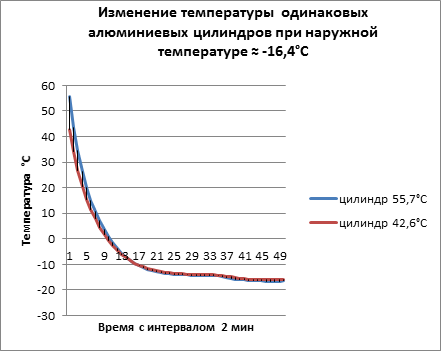
Рис. 5
Металл является хорошим проводником тепла. В данном эксперименте рабочее тело находится в твёрдом состоянии. В твёрдом теле не происходит перемещения атомов. Обмен энергией с окружающей средой происходит непосредственно между молекулами тела и молекулами окружающей среды.
Выводы
В данной статье предложено объяснение более быстрого остывания тела с большей температурой по сравнению с аналогичным телом с меньшей температурой. Как показывают проведённые эксперименты это свойство должно наблюдаться у всех веществ, при соответствующих начальных параметрах, а не только у воды.
Из графиков экспериментов и графиков компьютерной программы видно качественное совпадение изменения температуры в физических экспериментах и изменения кинетической энергии в компьютерных моделях. В экспериментах № 2, 3 наблюдается точка пересечения Аристотеля – Мпембы [5].
Для получения практической формулы необходимо расписать алгоритм на трёхмерное пространство, ввести соответствующие поправки в алгоритм. Для этого необходимо провести ряд экспериментов с различными веществами.

Fig. 6
Литература
1. Пирогов Н. Н. Соч.: Новое аналитическое доказательство 2 начала термодинамики, "Журнал Русского физ.-хим. об-ва. Часть физическая", отдел 1, 1886, т. 18, вып. 9.
2. Пирогов Н. Н. Основания кинетической теории многоатомных газов, "Журнал Русского физ.-хим. об-ва. Часть физическая", отдел 1, 1886, т. 18.
3. Пирогов Н. Н Несколько дополнений к кинетической теории газов, "Журнал Русского физ.-хим. об-ва. Часть физическая", отдел 1, 1885, т. 17, вып. 6, стр. 114—35.
4. Сивухин Д. В. Общий курс физики Том 2. Термодинамика и молекулярная физика, §56 Задача об остывании полупространства.
5. Mpemba E. B., Osborne D. G. Cool? // Physics Education. — Institute of Physics, 1969. — Т. 4, № 3. — С. 172—175. URL: https://ru.wikipedia.org/wiki/Эффект_Мпембы
6. В. Ф. Штром, программа AristotelesChart2.exe, https://drive.google.com/file/d/1TUi4ZszjXZJiACmvT6GAM-Oi4iyUAv89/view?usp=sharing
Отзыв из журнала Nature
An:vfstrohm@yahoo.de
25. Jan. 2018 um 17:42
Dear Mr Strohm,
Many thanks for your submission to Scientific Reports. However, we regret that
we cannot consider it for publication.
While your work could be of interest, I find that there is insufficient
evidence in the manuscript to clearly define and place into context the
research question being investigated. The literature cited is insufficient to
support the study rationale and the conclusions section does not adequately
address the link between the experimental data and the proposed model. Because
of these concerns we find that it does not fulfil the publication requirements
for Scientific Reports, that is, that papers must be original research and
technically sound in both method and analysis. Unfortunately, these
reservations are sufficiently important to preclude publication of this study
in Scientific Reports.
Thank you for the opportunity to consider your work. I am sorry that we cannot
be more positive on this occasion.
Best regards,
Dr. Mark Daly
Associate Editor
Scientific Reports
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.