Изопроцессы

Изохорный процесс. Примером такого процесса может служить

Охлаждение или нагревание газа в герметичном сосуде. Уравнение

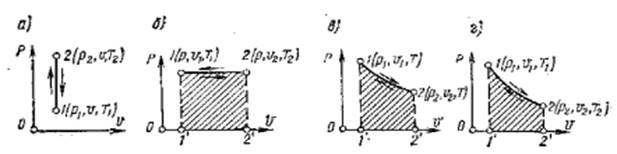
Процесса имеет вид w = const. Графическое изображение изохорного процесса в координатах p – w представляет собой отрезок прямой, параллельный оси ординат (рис. 9.3 а), который называют

Изохорой.

При нагревание газа его давление и температура возрастают, при охлаждении –

уменьшаются. Соотношение между параметрами можно найти из уравнений состояния в начале и в конце процесса p₁w= RT₁; p₂w = RT₂.

Поделив первое уравнение на второе, получим                                                             

Это закон Шарля, который гласит, что в изохорном процессе давление газа изменяется прямо пропорционально его абсолютной температуре.

Так как объем газа не измениться, то никакой работы в процессе не совершается.

Уравнение первого закона термодинамики в этом случае принимает вид

dq_w = du или q_w=∆

Таким образом , в изохорном процессе вся подведенная (или отведенная) теплота идет на увеличение (или уменьшение) внутренней энергии. С учетом уравнений и имеем

u=c_wm(T₂-T₁)    

Изобарный процесс. Так называется процесс изменения состояния газа, который осуществляет при постоянном давлении. Примером может служить процесс нагревания воздуха в помещении.

Уравнение процесса p=const, а графическое изображение на p – w –диаграмме – отрезок прямой, параллельный оси абсцисс, который называют изобарой.

         Из уравнения состояния идеального газа следует:

 =

         Это закон Гей-Люссака, который указывает на то, что в изобарном процессе объем газа изменяется прямо пропорционально его абсолютной температуре.

         В этом процессе одна часть теплоты, подведенной к рабочему телу, расходуется на изменение внутренней энергии тела, которое можно рассчитать по формуле (9.15), а другая часть – на совершение работы. В соответствии с уравнением (9.6)

Ap= = p(w₂-w₁)

Или

Ap = R(T₂ - T₁)

         Таким образом, если принять, что T₂ - T₁ = 1 °C, то газовая постоянная R есть работа, производимая 1 кг газа при его нагревании 1°C в изобарном процессе.

         Согласно первому закону термодинамики [см. уравнение (9.7)],количество теплоты, необходимое для осуществления этого процесса,

qp =  u + Ap,

Или с учетом формул

Qp = cwm(T₂ - T₁) + R(T₂ - T₁) = (cwm + R)(T₂ - T₁) = Cpm + (T₂ - T₁).

Если уравнение первого закона термодинамики для изобарного процесса записать в виде

qp =  u + p(w₂ - w₁) = (u₂ + pw₂) – (u₁ - pw₁)

То получим

qp =

Это означает, что теплота, сообщаемая газу в рассматриваемом процессе, идет на увеличение его энтальпии.

Изотермический процесс. Так называется процесс изменения состояния газа, который происходит при постоянной температуре. Уравнение этого процесса для идеального газа является выражением закона Бойла – Мариотта и имеет вид pw = const. Графическое изображение этого процесса на p – w – диаграмме представляет собой равнобокую гиперболу (рис. 9.3, в), которая называется изотермой. Процесс 1 – 2 – изотермическое расширение газа, которое возможно лишь при подводе теплоты, процесс 2 – 1 – изотермическое сжатие газа.

         Из уравнения состояния идеального газа следует:

w₁p₁ = p₂w₂

откуда

,

т.е отношение абсолютных давлений газа обратно пропорционально отношению объемов.

         Так как температура газа в процессе не изменяется (dt = 0), то внутренняя энергия также постоянна (u = const), т.е   u = 0. Следовательно, на основании первого закона термодинамики

Qт =Aт,

Т.е вся теплота, подведенная к газу, в изотермическом процессе расходуется на совершение механической работы.

         В соответствии с выражением и с учетом, что p = RT/w

 Имеем

Ат  = RT ln

Следует отметить, что математическое описание рассматриваемого процесса может иметь различный вид, а именно:

Ат = RT ln; Aт = p₁w₁ln.

         На основании выражения можно констатировать, что количество подведенной теплоты в изотермическом процессе также определяется по формулам.

Адиабатный процесс. Адиабатными называются процессы изменения состояния рабочего тела, осуществляемые без повода или отвода теплоты, т.е при dq = 0. Это необходимо и достаточное условие протекания данного процесса. При этом очевидно, что q=0. Но не всякий процесс, для которого q=0, будет адиабатным, так ака возможны процессы, в одной части которых теплота проводиться, а в другой такой же ее количество отводится. По этому q=0 – условие необходимое, но не достаточное.

Примеры адиабатного процесса: расширение или сжатие газа в цилиндре, выполненном из нетеплопроводного материала; расширение или сжатие, которое протекает настллько быстро, что теплообмен с окружающей средой не успевает произойти.

Графическое изображение такого процесса в координатах p – w представляет собой кривую, называемую адиабатой (рис. 9.3, г).

В соответствии с первым законом термодинамики

Dqад = du + dAад = 0,

Откуда      

Aад = u₁ - u₂.

         Следовательно, работа в процессе адиабатного расширения осуществляется за счет изменения внутренней энергии рабочего тела.

         Из уравнений имеем c_wdT + pdw = 0

         Принимая во внимания, что dT = (pdw + wdp), получаем

         Откуда

                            pdW + Wdp + pdw = 0

или )pdW + Wdp=()pdW+ W dp +pdW + W dp = 0.

         Обозначив Cp/Cw Через k, приходим  к уравнению kdpw + wdp = 0. Разделив его на pw, получим

                                      k+

         Результатом интегрирования будет выражение

                                      Kln w +ln p = 0,

Откуда

                                                                                                                 (9.29)

                                      Pwk=const,

Где k – показатель адиабаты ( если считать теплоемкости Cp и Cw постоянными, то для одноатомных газов k= 1,67: для двухатомных k = 1,4; для трех- и многоатомных k = 1,3).