
Как производятся арифметические операции в позиционных системах счисления?
Рассмотрим основные арифметические операции: сложение, вычитание, умножение и деление. Правила выполнения этих операций в десятичной системе хорошо известны — это сложение, вычитание, умножение столбиком и деление углом. Эти правила применимы и ко всем другим позиционным системам счисления. Только таблицами сложения и умножения надо пользоваться особыми для каждой системы.
С л о ж е н и е
Таблицы
сложения легко составить, используя Правило Счета.
|
Сложение в двоичной системе
|
Сложение в восьмеричной системе
|
Сложение в шестнадцатиричной системе

При сложении цифры суммируются по разрядам, и если при этом возникает избыток,
то он переносится влево.
Пример
1. Сложим числа 15 и 6 в различных системах счисления.
![]()
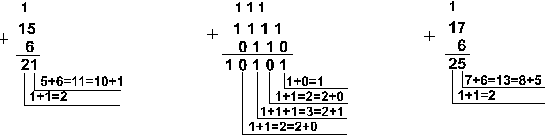
|
Шестнадцатеричная: F16+616
|
Ответ: 15+6 = 2110 = 101012 =
258 = 1516. |
Пример 2. Сложим числа 15, 7 и 3.
![]()
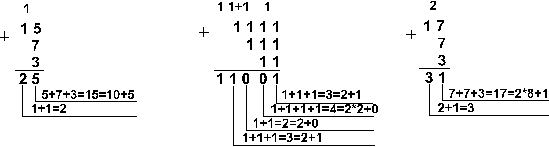
|
Шестнадцатеричная: F16+716+316
|
Ответ:
5+7+3 = 2510 = 110012 = 318 = 1916.
|
Пример 3. Сложим числа 141,5 и 59,75.
![]()
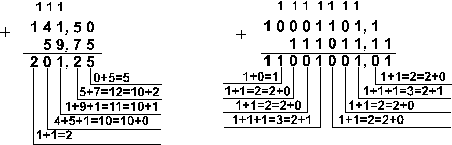
![]()
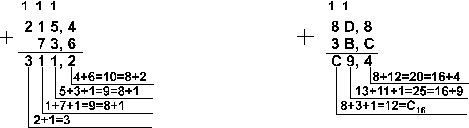
Ответ: 141,5 + 59,75 = 201,2510 = 11001001,012 =
311,28 = C9,416
Проверка. Преобразуем полученные суммы к десятичному виду:
11001001,012 = 27 + 26 + 23 + 20
+ 2-2 = 201,25
311,28 = 3 . 82 + 181 + 1
. 80 + 2 . 8-1 = 201,25
C9,416 = 12 . 161
+ 9 . 160 + 4 . 16-1
= 201,25
В ы ч и т а н и е
Пример 4. Вычтем единицу из чисел 102, 108
и 1016
![]()
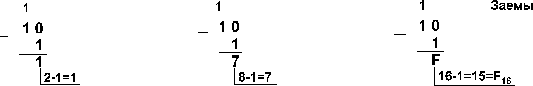
Пример 5. Вычтем
единицу из чисел 1002, 1008 и 10016.
![]()
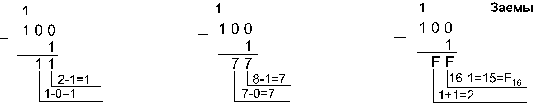
Пример 6. Вычтем
число 59,75 из числа 201,25.
![]()
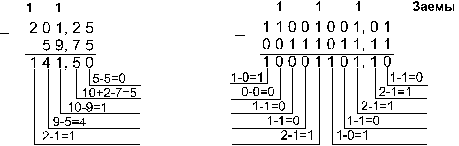
![]()

Ответ: 201,2510 - 59,7510 = 141,510 =
10001101,12 = 215,48 = 8D,816.
Проверка. Преобразуем полученные разности к десятичному виду:
10001101,12 = 27 + 23 + 22 + 20
+ 2-1 = 141,5;
215,48 = 2 . 82 + 1 . 81
+ 5 . 80 + 4 . 8-1 =
141,5;
8D,816 = 8 . 161
+ D .
160 + 8 . 16-1 = 141,5.
У м н о ж е н и е
Выполняя умножение многозначных чисел в различных позиционных системах счисления, можно использовать обычный алгоритм перемножения чисел в столбик, но при этом результаты перемножения и сложения однозначных чисел необходимо заимствовать из соответствующих рассматриваемой системе таблиц умножения и сложения.
|
Умножение в двоичной системе
|
Умножение в восьмеричной системе
|
Ввиду
чрезвычайной простоты таблицы умножения в двоичной системе, умножение сводится
лишь к сдвигам множимого и сложениям.
Пример
7. Перемножим числа 5 и 6.
![]()
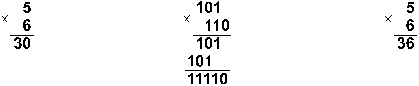
Ответ: 5 . 6 = 3010 = 111102 =
368.
Проверка. Преобразуем полученные произведения к десятичному виду:
111102 = 24 + 23 + 22 + 21
= 30;
368 = 381 + 680 = 30.
Пример
8. Перемножим числа 115 и 51.
![]()
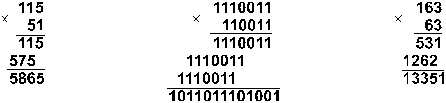
Ответ: 115 . 51 = 586510 = 10110111010012
= 133518.
Проверка. Преобразуем полученные произведения к десятичному виду:
10110111010012 = 212 + 210 + 29 + 27
+ 26 + 25 + 23 + 20 = 5865;
133518 = 1 . 84 + 3 . 83
+ 3 . 82 + 5 . 81 + 1
. 80 = 5865.
Д е л е н и е
Деление в любой позиционной системе счисления производится
по тем же правилам, как и деление углом в десятичной системе. В двоичной
системе деление выполняется особенно просто, ведь очередная цифра частного
может быть только нулем или единицей.
Пример
9. Разделим число 30 на число 6.
![]()
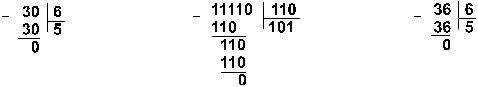
Ответ: 30 : 6 = 510 = 1012 = 58.
Пример 10.
Разделим число 5865 на число 115.
![]()

Восьмеричная: 133518 :1638

Ответ: 5865 : 115 = 5110 = 1100112 = 638.
Проверка. Преобразуем полученные частные к десятичному виду:
1100112 = 25 + 24 + 21 + 20
= 51; 638 = 6 . 81 + 3
. 80 = 51.
Пример 11. Разделим число 35 на число 14.
![]()

Восьмеричная: 438 : 168
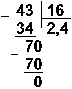
Ответ: 35 : 14 = 2,510 = 10,12 = 2,48.
Проверка. Преобразуем полученные частные к десятичному виду:
10,12 = 21 + 2 -1 = 2,5;
2,48 = 2 . 80 + 4 . 8-1
= 2,5.
4.11. Как представляются в компьютере целые числа?
Целые числа могут представляться в компьютере со знаком или без знака.
Целые числа без знака
Обычно занимают в памяти компьютера один или два байта.
В однобайтовом формате
принимают значения от 000000002 до 111111112.
В двубайтовом формате — от 00000000 000000002 до 11111111
111111112.
Диапазоны значений целых чисел без знака
|
Формат числа в байтах |
Диапазон |
|
|
Запись с порядком |
Обычная запись |
|
|
1 |
0 ... 28–1 |
0 ... 255 |
|
2 |
0 ... 216–1 |
0 ... 65535 |
Примеры:
а) число 7210 = 10010002 в однобайтовом формате:
![]()
б) это же число в двубайтовом формате:
![]()
в) число 65535 в двубайтовом формате:
![]()
Целые числа со знаком
Обычно
занимают в памяти компьютера один, два или четыре байта, при этом самый левый
(старший) разряд содержит информацию о знаке числа.
Диапазоны значений целых чисел со знаком
|
Формат числа в байтах |
Диапазон |
|
|
Запись с порядком |
Обычная запись |
|
|
1 |
–27 ... 27–1 |
–128 ... 127 |
|
2 |
–215 ... 215–1 |
–32768 ... 32767 |
|
4 |
–231 ... 231–1 |
–2147483648 ... 2147483647 |
Рассмотрим особенности записи целых чисел со знаком на примере однобайтового формата, при котором для знака отводится один разряд, а для цифр абсолютной величины – семь разрядов.
|
В компьютерной технике применяются три формы записи
(кодирования) целых чисел со знаком: |
Последние две формы применяются особенно широко, так как позволяют упростить конструкцию арифметико-логического устройства компьютера путем замены разнообразных арифметических операций операцией cложения.
Положительные
числа в прямом, обратном и дополнительном кодах изображаются одинаково — двоичными кодами с
цифрой 0 в знаковом разряде. Например:

Отрицательные числа в прямом, обратном и дополнительном кодах имеют разное изображение.
1. Прямой
код. В знаковый разряд помещается цифра 1, а в разряды цифровой части числа
— двоичный код его абсолютной величины. Например:
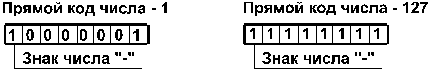
2. Обратный
код. Получается инвертированием всех цифр двоичного кода абсолютной
величины числа, включая разряд знака: нули заменяются единицами, а единицы —
нулями. Например:

3. Дополнительный
код. Получается образованием обратного кода с последующим прибавлением
единицы к его младшему разряду. Например:
![]()
Обычно отрицательные десятичные числа при вводе в машину автоматически преобразуются в обратный или дополнительный двоичный код и в таком виде хранятся, перемещаются и участвуют в операциях. При выводе таких чисел из машины происходит обратное преобразование в отрицательные десятичные числа.
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.