ПРАВИЛО

ОБРАЗЦЫ

ЗАДАНИЯ

а ас

допустимых значений переменных.

Задача 1.

Сократить дробь

аЬ—Ьс

а² —2ас + с²

Решение:

Задача 2.

Привести дробь

знаменателю х) — у^а• к

Решение:

Сократить дроби:

7(х ² +20+ у?)

        ау                   3х+ Зу                b² —4bc+4c

Привести дроби к общему знаменателю: з       2

5) х— у

Сократить дроби:

                                 —а.² +2ab—b ²                                   48-1

                                   7)8)                          + 48

                               2a-2b                  — 4с

Привести дроби к общему знаменателю; 9) Е и 2; 10) 3х 2— Зу х» 4у

Сократить дроби:

          Ьу              3(Т² +2T+l)                 9с² — 4

11) —          12)      3х+ Зу            13) 98 -12с+4

Привести дроби к общему знаменателю:  2

14) — и15) 2p+2q ^И p—q

riPABHJIA

OBPA3ub1

a                 b

            c—d           1

c^l —d² C+d

Ha.üTM cyMMN paaøoc•rx:

1)

        4)             

2

x—y

8)

        4      4 '          3c          3c '

2mn

9)10)

11)

14)

TIPABHJIO

OBPA3E11

3AAAHMfl

1)  Haň'1'M 06łqnň

azaxezxren.

2)  BMIIOJIH_HTb AeňCTBHR.

(a —b)² a² —b

I) 0614Eů anaxegaren:

2)

(a —b)² a² —b ²

ar + br + ay—by

HaňTH CYMMN pa3HocTM npoőei:

                    1         1

            4)                        '5)

a2b3 a2b3

         7)

1

9)

3a-2b

11) —-4 12)

3 2

1

14)

3c² +5ab b² —3ac

                      18)                               '

bc

 IIPABWIA

OBPA31-1b1

b d bd npø aonycTHMb1x

azaqeHMqx nepeNeHEb1x;

3a² —6ab a ⁴ —9b⁴

a(a² —2b² )

7(a-2b)

         2a              2a• 35ab

—.35ab=

HaiTH

10 3 '

11POHaBeAeEge Äp06eü:

2 4 —3a

2) 8a b

a²b —4b

4)

             3ab2        g² —2ab

HaiTH ZPOH3BeaeEze Äp06ei:

HaüTH

11)

13)

11POH3BeAeHne Ap06eü:

12) 4m n

14)

15)

IIPABHJIO

OBPA311b1

a             c ad

b            • d bc apn

azaqeznax nepeMeHHb1X.

x² +ï x² —»•

qacTEoe

                           18a²b² 6ab³                x² —y² x

5cd • 5c²d⁴ ; ) 6x²y² • ³

4) 4p2 —9q2 2Q+3aq. 5) x² —25 p2q2 2pq x² —5x x² +4x

25c                            3bx

 ay

3m^Ž —3n² 6m—6n

9)10)

m2p

²

8)

c + d c² +Cd

11)

8b2cd 7cd

                   12)                     '

25z                                      9a2 12a3

14)           15)

18) a² —25 a² +5a9 ; a² -3a• a²

•

TIP

WIA

OBPA3Ub1

VilPOCTHTb:

Peuewue:

Tax rcax 110ÃRopezgoe

BblpaxeHHe —X HeorpnuaTeJtbHO, TO x SO, H I xl

OROHqa•reJ1bEO nonyqaeN OTBeT: —21 .

Yapo.CTHTb.•

13)

r-IPABMJIA

OBPA31.1b1

3AV,HHfl

V-VI.

Tax garę no S'CJIOBHIO z⁷  z 20.

Ho F al el , a Tarę    Rag zžO,TO Iz³ 1—z³ .

       Mrax,    z³ cz.

  Buzec•rn MHOXHT&U H3-110A Ropza:

                         12)

13)         rae

14)        F; 15)

IIPABHJIO

OBPA3EU

Hr06b1 BHeCTH

MHOKHTeJ1b nou

3Hax KOPHH,

HYKHO

1)     ero

norea3aT•eüb c•reneHH, 2) eCJIH 8TOT

0TPHuareJ1eH, 110MeHKTb 3Hayc nonyqeHHoro

3ueHMTb BblPaxeHHe aJj

KOPHeM HJIH

BHpaxeHHeM, epay lipomBOUOJIOKHHM.

PeueHue.•

ecam , ecnH Ke a '0, TO aJj--Fb.

B nepB0M cnyqae nonyqH31ca KBaupaTHb1Ü KOPeHb, a BO BTOPOM — BHpaxeHHe,

KB8APaTHOMY KOPHYO.

3ueHHTb BMpaxeHHe KOK)HeM UPOTHBOnOJXOKHHM eMY BMpaxeHHeM:

         1) 245;. 2) -0,5Jî;

3)q; , rxe x

4)aça ;     

6) -315;

8) yG,rue y 40;

                                                 10) nü;

               11) 55;   12) 0,145;

13)  c² ü;

14)  -Et; 15) 47.

ПРАВИЛО

ОБРАЗЦЫ

• Уравнение вида = О решается так: ar ² = О , х² =О (так как а $0),

Уравнение вида

решается так:

Уравнение вида

решается так: gr2               

, так как а $0;

с

О, корней нет; а

Решить

а) 2х ² +8=0, б) 3х² -2х—0.

в) г) 6х² =0.

Решение:

а) 2х² +8=0 — уравнение виа ч-с=О;

2х ² +8=0,  Р =-4.

Ответ: корней нет.

г) 6х² = О — уравнаие вида ах

6х² =0, х^а —0, х=О.

Ответ: О

Решить уравнения:

1) 3х ² +1=0;

-16=0;

б) 5х² -5-0,

7)    3х² +6х—0;

8)    2х² +8=0;

11)   2х² +8=0;

12)   2х ² —3х=О;

13)   5х ² -10=0;

14)   Р -0;

15)

ПРАВИЛО

                    ОБРАЗЦЫ

ЗАДАНИЯ

Чтобы решить по формуле квадратное уравнение

+Ьх+С=О ,

вычислить его. дискриминант

D = b ⁱ —4ас ;

если , записать ответ: корней нет;

если D = 0, вычислить единственный корень уравнения по формуле

если D > О , вычислить два корня уравнения по формуле

X1,i =

2а

Решить уравнения:

а) 8х² +4х+3=0,

б) х² —6х+9=0,

в) 5х² Решение:

а) 8х² +4х+3=0;

D=4² -4-8.зе-80<0. Ответ: корней нет.

б) х² —6х+9=0;

6

-3.

2

Ответ: (3

в) 5х² —3х—2=0;

Ответ; (—0,4; l}.

Решить уравнения:

6)                                 5х²

7)                                 3х² +6х+3=0;

8)                                 +4х+5=0;

9)                                 4х² -11х-7=0;

10)                             -45х-0;

11) 2х² +7х-9=0; 12) 2х² -4х+2=0;

13)

14)                             х^а +5х+6=0;

15)                             -27Х-0.

ПРАВИЛО

ОБРАЗЕЦ

При решении числовых неравенств можно: — переносить слагаемые из одной части неравенства в другую, изменяя знаки этих слагае-

— делить обе части неравенства на одно и то же положительное число; — делить обе части неравенства на одно и то же отрицательное число, изменяя знак неравенства.

Решить неравенство: -2(х-3) > 3(X+5).

Решение:

Раскроем скобки: -2х+6 > 3х+15, перенесем слагаемые с неизвестным влево, а слагаемые без неизвестных — вправо, меняя их знаки: -2х-3х > 15-6, приведем подобные:

—5х > 9.

разделим обе части неравенства на отрицательное число —5 , меняя знак неравенства:

—1,8

Решить неравенства:

1)

4) 6—х < 8+х; 5) 20-4) > 5-7х;

7)        Т—хх 7 ;

8)        3х-2 2х;

9)        < 74-х; 10) ф+3) > 4—6х ;

11)

12)

13)

14)  4+Х < 4+2х ;

15)  —30+1) < 4—х.

ПРАВИЛО

ОБРАЗЦЫ

ЗАДАНИЯ

Если у квадратного уравнения ах? +Ьх-нс—О есть корни xt И .t2 , то квадратный трехчлен

+ЬХ+С можно разложить на множители: ах2

Если у квадратного уравнения C² +bx+c= О нет корней, то квапатный трехчлен at² +ьх+с нельзя   разложить на множители.

Если у квадратного уравнения +Ьх-ьс=О есть один корень , то квадратный пехчлен at² + ЬХ+С МОЖНО разложить на множители: ar² +bx-ec =

Следующие квадратные трехчлены разложить на множители, если это возможно: 00х2-5х+2,

б) 9х² +6х+1,

в) Р —2х+3.

Решение:

а) Составим уравнение 2х ² —5х+ 2 = О ,

что можно записать и так:

.

что можно записать и так: 9х2

в) Р —2х+3=0, D=—8 О, корней нет. Значит, трехчлен х^а —2х+3 нельзя разложить ва множители.

Разложить на множители, если это возможно:

1)  3х² 45х-8=0:

2)  Р +5х+10-0;

3)  7х² -14х+7=0;

4)  —х² +3х+4=0;

5)  —16х—0 ;

б) 5х² + х— ; 7) 3х ² +6х+3 = О;

8) х^а +4х+5=0;

11)   2х² +7х-9=0;

12)   2х² -4х+2=0;

13)   Р-10х+30=о;

14)   Р +5х+6=0;

15)

ПРАВИЛО

ОБРАЗЕЦ

Построить параболу У = ar² +Ьх-нс

можно так:

1)            найти абсциссу вершины параболы по формуле хо —

2)            найти ординату вершины параболы до формуле

Уо — 4а или по формуле

Уо = + Ьхо +с; З) при вершине (хо,уо) построить параболу

Построить график

3)

Построить трафики:

+5х—6 ;

2) у=Р+5х;

5) у=х² +х+1 ;

9).= 0,5х² + Х+О,5 ;

11)

12)

13)

14)

15) у=х² -2х+2.

Карточка

14. Решение систем уравнений

ПРАВИЛО

ОБРАЗЕЦ

ЗАДАНИЯ

Если одно из неизвестных в системе стоит в первой степени, то можно попытаться решить эту систему методом подстановки.

Решить систему:

Решение:

Ив второго павнения

Подставляем это выражение в первое уравнение вместо х :

   (7-у)² +У²           ,

2у² —10+24=0,

Подставляем и уа в уравнение х = 7— у :

Решить системы:

²

                                                     у—х = О,            3)

1)

2х0+3=0;

-6,

5)

2х—3у 6;

6)

² = 12,

7)

9)

ху = 8, x+Y+3=O;

2 -16;

11)

²

у—х = О,

15)

13)

-3у² -52, -x=14.

OOPMYJ1b1

OBPA3EU

 .

38110JIHHTb

0TRYÃa n=8, a9 —21+2=23.

3) an+l —an +d,

Omaem:

3ano.ZEHTb 'ra6JIH14Y

OOPMYJ1b1

OBPA3EL1

3anOJIHHTb Ta6anuy

PetueHue:

1) sn= ^al + ^an

7+21

.4 56 ;       

Omeem:

•ra6JIHAY

OOPMYJ1b1

OBPA3EL1

bn+l =bnq; bn = hqn-l.

BanoJIHHTb •ra6nøay

o-•rxyaa n = 4 ,

9=-18 q,

0TKYAa q ——0,5.

Omeem:

3a110JIH¼Tb •ra6JIH11Y

OOPMVJ1b1

OBPA3E11

EcJIM q

TO cyMMY nepBbtx n qaeEOB reoue•rpøgecnporpeccHH

çyNMY nepBb1X qeTNpëx qaeEOB reoueTpggecRoh aporpeccun, y ROTOPOü nepBbIi pageg 7, a qeTBëpTNü pueg — 56.

Peuzercue:

HahAëM q : b4=-56, éq³ —-56 ,

3an0JIHWt'b •ra6auay

ПРАВИЛА

ОБРАЗЕЦ

Геометрическая протк рессия называется бесконечно убывающей, если lql<1. У неё (при

бесконечном увеличении числа членов) S стремится к чйслу S, называемому суммой прогрессии и вычисляемому по формуле:

Найти первый член бесконечно убывающей геометрической прогрессии, знаменатель которой равен —0,1, а сумма S равна 6.

Решение:

1+0,1

Заполнить таблицу

ЗАДАНИЯ

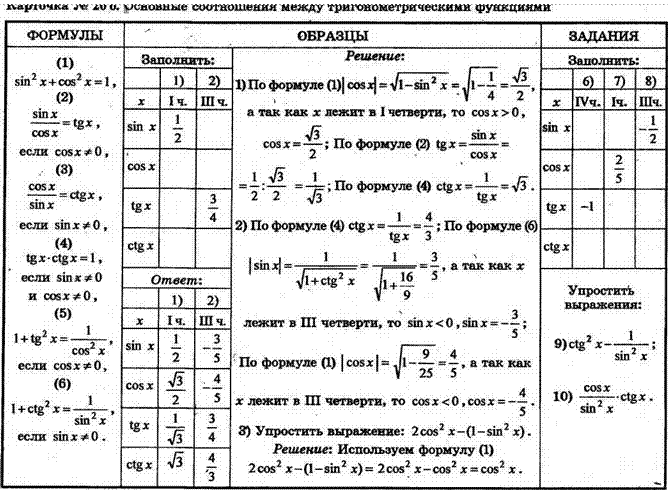
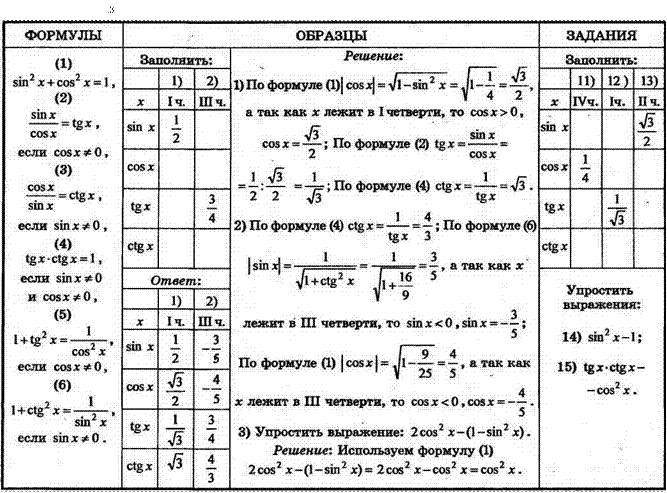
sin ² X+cos² x=1,

(2) sin х

= tgx , ст х если c0sx$o,

(3)

cosx sin х если sinx*O,

              (4)  

(5)

сое х если сох * О,

(6)

Решение:

sinx

      COS х              ; По формуле (2) tgx = —

cos х

 = Д— ; По формуле (4) ctg х

2) По формуле (ф ctg х = — ; По формуле tgx З

(6)

х

;

как

.

х) .

х.

х

sin х

cos х

соз х

Ответ:

Упростить

4)      cos² х

5)  E•cos² х ,  smx

х

1 ч.

Ш ч.

cos х

5

ФОРМУЛЫ

ОБРАЗЦЫ

Формулы приведения позволяют выразить

тригонометрические функции углов 90⁰ ±х ,

 3600±х через тригонометрические функции угла х .

Для этого:

1)               функция в правой части равенства берётся с тем же знаком, какой имеет исходная функция, если считать х углом первой четверти;

2)               для углов 180⁰ ±x В

360⁰ ±x исходная функция сохраняется, а для углов 90⁰ ±х и 270⁰ ±x синус меняется с косинусом, а тангенс с котангенсом.

1. Выразить cos(270⁰ + х) через тригонометрическую от Х .

Решение:

1) Если х — угол четверти, то

270⁰ + х — угол IV четверти, в которой положителен.                                

В правой части поставим -е.

2) Для 270⁰ + х название функции меняется. В правой части пишем sinx . Ответ:

2. Выразить   через оигонометрическую функцию от х . Решение:

1) Если х— угол четверти, то

180⁰ —х— угол П четверти, в которой котангенс отрицательный. В правой части доставим —

2) Для 180⁰ —х название функции ве меняется. В правой части пишем ctg х .

Ответ:  х.

З. Найти значение sin57(P .

Решение:

5700=3600+2100  ,

Выразить через тритнометрические функции углах :

Вычислить: 5) cos765⁰ .

Выразить через тригонометрические функции углах :

9) ctg(90⁰ — х).

Вычислить; 10) tg 750⁰ .

Выразить чера тригонометрические функции углах :

Вычислить: 15)ctg1830⁰ .         

ФОРМУЛЫ

ОБРАЗЦЫ

sin(x + у) = sinxcosy+ cosx±y sin (х— у) sinxcosy—cosxsin у , cos(x + у) = cosxcosy-' sinxsiny , cos (х — у) = cosxcos Y+Sin xsin у , tgx+tgy tg(X+ У) =

1 —tgxtgy tgx—tgy

tg(x — У) =

1 + tgxtgy

1)               Пребра.овать до фомулаы в»ажение cos(45⁰ + х).

Решение:

Воспользуемся формулой косинуса суммы:

cos(45⁰ + х) = cos45⁰ cosx—sin 45⁰sinx =

         —sinx .

     2             2

2)               Вычислить 15⁰ .

Решение:

Так как 15⁰ = 45⁰ —30⁰ , воспользуемся формулой тангенса разности: tg 45⁰ — tg 30⁰

1 + tg 45⁰ № ЗО^О

1   1

Преобразовать по формулам сложения:

2)tgV-x).

3) sin75⁰ ;         4) cosl 050 ;

5)tg15C.

Преобразовать по формулам сложения:

7)    tg(30⁰ +x).

8)    sin15(P;      9) cos75⁰ ;

10) tg105⁰ .

Преобразовать по формулам  сложения: 11) sin(60⁰ +x); 12) 0-450).

13) sin105⁰ ; 14) cos150⁰ ;

15) tg7$

ФОРМУЛЫ

ОБРАЗЦЫ

ЗАДАНИЯ

sin 2sin xcosx , соф = сор x—sin² х, 2tgx tg2x

1—tg2x

cosxeo, cos2X*O.

5

1.              НайтиЈп2х, есдисо$ х=—, В х— угол четверти.

Решение: sin2x = 2sinxcosx , так что сначала нужно ga*msin х ,

а так как х — угол [V четверти,

12

Tosinx.<O, откуда sinx=— 13

Теперь находим sin 2х :

120 sin2x = 2sinxcosx =

169

2.              Найти , если tg х = б . Решение: Воспользуемся формулой тангенса двойного угла:

2tgx 2$ tg2x

1—tg x 1—3

З. Вычислить 2sin2cos2.

8 Решение: Воспользуемся формулой синуса двойного угла, читая её справа налево:

2sinEcos2=sin2•——

               8                        4 2

пользуясь формулами двоййого угла:

1)sin2x , ec;msin х , х — угол П четверти;

1

2) cos2x, если cosx=— 3' З) tg ь, если tg х=2;

       4) 2sin2cos2;       5) sin 120⁰ ;

12 12

6)sin 2х , еслисш х = — — угол 1 четверти;

2

7)   cos 2х, если sin х=——; 7

8)   Ох, если tgx=3;

9)   2sin45⁰ cos45⁰ ;       10) cos120⁰ ;

2

                            х             х —утлШчет—ти;

5

12)  cos 2х, если cos х

13)  Щ 2х,если

14)  2sin2cosE;       15) tg 120⁰ .

ФОРМУЛЫ

ОБРАЗЦЫ

sinx + sin у = 2sin

Sin х — sin у = 2sin

сох + cos у ='2cos

cosx — cos у = 2sin

sin(x + у) tgx+tgy= cosx•cosy sin(x — у) tgx—tgy=                                cosx • cos у

2

2

2

1)           Разложйть на множи-

тели выражение Sin 5x•sin 2х. Решение:

По формуле

суммы синусов sin 5х + sin 2х =

= 2sin3,5x • sin1,5x.

2)           Преобразовать в произведение tg2y— tg у

Решение:

По формуле разности тангенсов sin у tg2y—tgy =

cos2y•cos у

З) Вычислить cos 75⁰ 5⁰.

Решение: По формуле

разности косинусов cos 75⁰ — ст 15⁰ =

—2sin450.sin(-300)——— 2

Преобразовать по формуле: 1) sin 40⁰ + sin 60⁰ ; 2) tg3x+tgx•.

                                 4) cos2—cos  '

               8         8               12        12

5) cos—+cos!.Зп

8

Преобразовать по формуле:

6) sin 2y—sin 5у ;

+ tg2x . Вычислить:

    8)sin75⁰ +sin15⁰ ; 9)cos ——cos—ⁿ   31

8 '

10) cos—+ 51 сор .

8

Преобразовать по формуле: 11) cos3x—cos5x ; 12) tg40⁰ ,tg50⁰ .

Вычислить:

13) яп•

15) sin — +sm — 8