Муниципальное общеобразовательное учреждение Солтановская основная общеобразовательная школа муниципального района город Нея и Нейский район Костромской области

 

 

 

                                                                                                                                        Приложение 

к рабочей

                                                                                                                                          программе

  

 

Контрольно-измерительные материалы для проведения промежуточной аттестации по предметам «Алгебра» и «Геометрия»

в 7-9 классах

 

 

 

Учитель математики ПКК: Булохова С.Б.

 

 

 

 

 

С. Солтаново 

 

Контрольно-измерительные материалы  для проведения промежуточной аттестации  по алгебре 7-9 классы

 

СПЕЦИФИКАЦИЯ контрольных измерительных материалов для проведения промежуточной аттестации по алгебре   в   7 классе

 

1. Назначение контрольных измерительных материалов

 Определение объективной  индивидуальной оценки  уровня обученности обучающихся  7 классов по предмету  алгебра.

    Объектами проверки выступают элементы содержания, а также умения, способы познавательной деятельности, определенные требованиями Федерального  государственного образовательного стандарта: владение основными алгоритмами; знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.); умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.   Предлагаемый комплекс заданий нацелен на дифференцированное выявление уровней подготовки учащихся по предмету. Задания КИМ различаются по характеру и уровню сложности, который определяется способом познавательной деятельности, необходимым для выполнения заданий. 

 

2. Общая характеристика структуры и содержания работы

Задания тестовой работы ориентированы на учебник «Алгебра7» (автор А.Г.Мордкович)   и составлена в полном соответствии со «Стандартом основного общего образования»

Работа состоит из семи заданий: 5 заданий базового уровня сложности, которые обеспечат проверку достижения обучающимися уровня обязательной (базовой) подготовки по  алгебре за 7 класс; 2 задания повышенного уровня сложности. Все задания требуют записи решения и ответа.

3.  Время выполнения .  

На выполнение всей работы отводится 45 минут. 

Дополнительные материалы и оборудование. Линейка, карандаш.

4.Система оценивания

 

Тип задания	Критерии оценивания	Кол-во баллов	Итого
А1	Верная числовая подстановка в выражение	1	2
	Верно выполнены    арифметические       действия         с рациональными числами ИЛИ  Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная	1   0,5

 

	последовательность всех шагов решения
А2	Верно раскрыты скобки	1	2
	Верно выполнены арифметические действия при приведении подобных слагаемых ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1     0,5
А3	Верно применены  основные свойства степени с целыми показателями	1	2
	Верно выполнены соответствующие вычисления ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1   0,5
А4	Верно применена формула разности квадратов	1	3
	Верно вынесен общий множитель за скобки	1
	Верно выполнено сокращение алгебраической дроби	1
А5	Верно дан ответ на вопрос задачи по графику	1	1
В1	Верно найдены  координаты точек линейной функции   ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1   0,5	4
	Верно изображена координатная плоскость	1
	Верно      построены            точки      с      рассчитанными  координатами	1
	Верно построен        график            линейной             функции         по отмеченным точкам	1
	Верно определены координаты заданной точки х и у	1	4
	Верно подставлено значение х в формулу функции	1
	Верно выполнены    арифметические       действия         с рациональными числами ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1   0,5
	Верно записан ответ на вопрос	1
В2	Верно определено из какого уравнения легче выразить переменную и выразили   одну переменную через другую	1	5
	Верно      осуществили       подстановку        полученного выражения в другое уравнение	1
	Получили верный ответ при решении линейного уравнения ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1   0,5
	Верно рассчитали другое неизвестное ИЛИ Получен неверный ответ из-за вычислительной ошибки, но при этом имеется верная последовательность всех шагов решения	1   0,5
	Записали правильно ответ к системе уравнений ИЛИ Верно записана         форма             ответа             с             полученными вычислительными ошибками.	1   0,5
	Итого	23	23

  

Максимальный балл за всю работу – 23 

Шкала пересчета первичного балла за выполнение   работы в отметку по пятибалльной шкале

Отметка по пятибалльной шкале	«2»	«3»	«4»	«5»
Общий балл	0-8	9-14	15-19	20-23

 

5. Кодификатор

 

Тип задания	Название  раздела содержания	Контролируемые виды деятельности, умения
А1	Алгебраические  выражения	Находить значение числового выражения по значению входящих в него букв
А2	Одночлены и многочлены	Раскрывать скобки в выражениях и приводить подобные слагаемые
А3	Степень  с целым показателем	Применять свойства степени для упрощения числового выражения и
		нахождения его значения
А4	Алгебраические дроби	Выполнять  разложение многочленов на множители и сокращать дробь
А5	Линейная функция и её график	Интерпретировать  график реальной зависимости между величинами
В1		Рассчитывать  координаты точки графика функции на плоскости, строить точки по заданным координатам, строить график функции.
		Определять алгебраическим методом принадлежность точки плоскости графику функции
В2	Системы двух уравнений с двумя неизвестными	Применять алгоритмы решения системы двух уравнений с двумя неизвестными и линейного уравнения.

 

 

Инструкция для обучающихся по выполнению работы

Итоговая  работа состоит из 7 заданий, из которых 5 заданий базового уровня сложности,   2 задания повышенного уровня сложности. Все задания требуют записи решений и ответ.

На выполнение итоговой работы по алгебре отводится 40 минут

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются.

Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Общее количество баллов может быть уменьшено на 1 балл в следующих случаях:

-   допущены грамматические ошибки при написании математических терминов;

-   небрежно оформлена работа;

-   небрежно выполнен рисунок к задаче.

 

Желаем успеха!

                                                                    

 

Вариант 1

А1. (2балла)  Найдите значение выражения 4х² + 3у при х = - 2, у = -9.

А2. (2балла)  Упростить выражение  -12х+3ху – 2(х+3у).

А3. (2балла)  Найдите значение выражения:  .

                      А4. (3балла)  Сократить дробь:         .

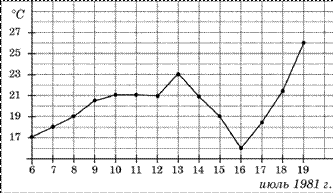
А5.   (1балл )  На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какой была наибольшая среднесуточная температура за указанный период.

В1.   (8баллов)      а) Постройте график функции у = 3 – 2х.

                                                              б) Принадлежит ли графику этой функции точка М(8; -19)?

  В2.   (5баллов)    Решить систему уравнений:  

Инструкция по выполнению работы

Итоговая  работа состоит из 7 заданий, из которых 5 заданий базового уровня сложности,   2 задания повышенного уровня сложности. Все задания требуют записи решений и ответ.

На выполнение итоговой работы по алгебре отводится  1 час 20минут (80 минут).

При выполнении заданий можно пользоваться черновиком. Записи  в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются.

Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Общее количество баллов может быть уменьшено на 1 балл в следующих случаях:

-   допущены грамматические ошибки при написании математических терминов;

-   небрежно оформлена работа;

-   небрежно выполнен рисунок к задаче.

 

Желаем успеха!

 

 

 

Вариант 2

А1. (2балла)   Найдите значение выражения 3а² + 2b при а= - 3, b= - 4. 

А2. (2балла)   Упростить выражение  -6х+5ху – 2(х+2ху).

А3. (2балла)   Найдите значение выражения:  .

А4. (3балла)   Сократить дробь:     .

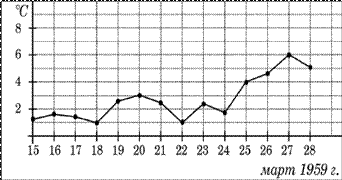А5.  (1балл)    На рисунке жирными точками показана среднесуточная температура воздуха в Пскове каждый день с 15 по 28 марта 1959 года. По горизонтали указываются числа месяца, по вертикали - температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку, какой была наименьшая среднесуточная температура за указанный период

 

В1. (8баллов)            а) Постройте график функции у = 2 – 3х.

б) Принадлежит ли графику этой функции точка N(9; -25)? 

                      В2. (5баллов)    Решить систему уравнений:                                

 

 

  

 

 

Спецификация контрольно- измерительных материалов для проведения промежуточной аттестации по алгебре за курс 8 класс

1. Назначение работы

- оценить уровень  предметных компетенций  учащихся 8 классов  по алгебре 2. Общая характеристика структуры и содержание работы

Задания тестовой работы ориентированы на учебник «Алгебра8» (автор А.Г.Мордкович)   и составлена в полном соответствии со «Стандартом основного общего образования»

Часть 1 направлена на проверку овладения содержания курса алгебры 8 класса на уровне базовой подготовки. Эта часть  содержит 7  заданий.  При выполнении заданий части 1об учающиеся должны продемонстрировать базовую математическую компетентность. В этой части проверяется владение основными алгоритмами, знание и понимание ключевых элементов содержания (математических понятий, их свойств), применять знания к решению математических задач, не сводящиеся к прямому применению алгоритма, а также  применять математические знания в простейших практических ситуациях.

Часть 2 направлена на проверку владения материалом на высоком и повышенном уровнях. Ее назначение – дифференцировать хорошо успевающих  школьников по уровню подготовки, выявить наиболее подготовленную часть обучающихся 8 классов.  Эта часть содержит 3 трудности - от относительно простых до сложных, предполагающих свободное владение материалом и высокой математической культуры.

3. Время выполнения  работы

На выполнение контрольной работы отводится 45 минут

Дополнительные материалы и оборудование. Линейка, карандаш.

4.Система оценивания 

За выполнение каждого задания ученик получает определенное число баллов. 

Часть 1	Часть 2			Итог
Задания, №	Задания, №	Задание, №	Задания, №	Задания, №
1-7	8	9	10	1-10
1	2	3	4	16

В случае правильного выполнения задания части 1 учащемуся засчитывается 1 балл, если ответ неверный или отсутствует – 0 баллов. 

Задание части 2 считается выполненным правильно, если учащийся выбрал правильный путь  решения, из письменной записи решения понятен ход его рассуждений, получен верный ответ. В этом случае ему выставляется полный балл (2 ,3 или 4 балла), соответствующий данному заданию. Если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения, то учащемуся засчитывается, на 1 балл меньше указанного.

Исправления и зачеркивания, если они сделаны аккуратно, в каждой части итоговой контрольной работы, не являются основанием для снижения отметки.

 

 

 

 

 

Таблица перевода суммарного балла в 5-балльную шкалу

Отметка по 5балльной шкале	«2»	«3»	«4»	«5»
Первичный балл	Менее 5 баллов	5-7 баллов	8-10	9-16

Критерий оценивания части 2

Критерий оценивания задания 8

Содержание критерия	Баллы
Правильно выполнено задание	2
Решение доведено до конца, но допущена ошибка или описка вычислительного характера, и ее учетом дальнейшие шаги выполнены  верно.	1
Другие случаи, не соответствующие  перечисленным выше критериям.	0
Максимальный балл	2

Критерий оценивания задания 9

Содержание критерия	Баллы
Правильно выполнено задание	3
Правильно найден дискриминант квадратного уравнения. Правильно составлено линейное неравенство, но допущена описка или ошибка вычислительного характера, и ее учетом дальнейшие шаги выполнены верно.	2
Правильно найден дискриминант. Правильно составлено линейное неравенство. Неравенство не решено.	1
Другие случаи, не соответствующие перечисленным выше критериям.	0
Максимальный балл	3

Критерий оценивания задания 10

Содержание критерия	Баллы
Правильно  составлено и решено уравнение, получен верный ответ.	4
Правильно  составлено уравнение, но при его решении допущена вычислительная ошибка, с ее учетом решение доведено до конца.	3
Правильно  составлено уравнение, но оно не решено.	1
Другие случаи, не соответствующие перечисленным выше критериям.	0
Максимальный балл	4

 

5. Кодификатор

№ п/п задания	Проверяемые элементы
	Часть 1
1	Решение квадратного уравнения.
2	Свойства квадратного корня
3	Линейное неравенство с одной переменной.
4	Степень с целым показателем
5	Преобразование алгебраической дроби
6	Квадратное неравенство с одной переменной
7	Функции и графики.
	Часть 2
8	Сокращение алгебраической дроби.
9	Квадратное уравнение с параметром. Линейное неравенство с одной переменной.
10	Решение текстовых задач

 

 

 

 

 

Инструкция для обучающихся по выполнению   работы.

       На  выполнение работы отводится   45 минут

Работа состоит из двух частей и содержит 10 заданий.Часть 1 содержит 7 заданий обязательного уровня. 

 Внимательно прочитайте задание и выполните его на черновике

При выполнении   заданий части 1 необходимо записать только ответ. Часть 2 содержит 3 более сложных заданий. К каждому заданию надо дать подробное  и обоснованное решение.  

Исправления и зачеркивания, если они сделаны аккуратно, в каждой части контрольной работы, не являются основанием для снижения отметки.

При выполнении работы советуем не торопиться, проверять полученный ответ, творчески подходить к решению каждого задания.

                             Желаем успеха

Часть 1

1.        Решите уравнение х² +3х -18 =0.

Ответ: ________________________________

2.        Найдите значение выражения  .

Ответ: ________________________________

3.Решите неравенство 18-8(х-2)  10-4х.

Ответ: _________________________________

4.Вычислите значение выражения  16(2^-3)².

1) 8;        2)  ;             3) 4;                4)  .

                      5.Упростите выражение  ( -    .

Ответ: __________________________________

6.При каких значениях х верно неравенство  - х² + 2х +8  0?

Ответ: _________________________________________

7. Найдите абсциссу точки пересечения графиков функций у =  и у= 2.

Ответ: _________________________________________

 

Часть 2

8.(2 балла)  Сократите дробь .

9.(3 балла) При каких значениях параметра m уравнение    х² -2х -3m=0    имеет  два корня.

10.(4 балла)  Моторная лодка прошла 28км по течению реки и 25км против течения, затратив на весь путь столько же времени, сколько ей понадобилось бы на прохождение 54 км в стоячей воде. Определи скорость лодки в стоячей воде, если скорость течения реки 2 км/ч.

 

 

 

 

Спецификация контрольно- измерительных материалов для проведения  промежуточной аттестации по алгебре за курс 9 класса

4. Назначение контрольных измерительных материалов

 Определение объективной  индивидуальной оценки  уровня обученности обучающихся  9 классов по предмету  алгебра.

    Объектами проверки выступают элементы содержания, а также умения, способы познавательной деятельности, определенные требованиями Федерального  государственного образовательного стандарта: владение основными алгоритмами; знание и понимание ключевых элементов содержания (математических понятий, их свойств, приёмов решения задач и проч.); умение пользоваться математической записью, применять знания к решению математических задач, не сводящихся к прямому применению алгоритма, а также применять математические знания в простейших практических ситуациях.   Предлагаемый комплекс заданий нацелен на дифференцированное выявление уровней подготовки учащихся по предмету. Задания КИМ различаются по характеру и уровню сложности, который определяется способом познавательной деятельности, необходимым для выполнения заданий. 

 

5. Общая характеристика структуры и содержания работы

Задания  работы ориентированы на учебник «Алгебра9» (автор А.Г.Мордкович)   и составлена в полном соответствии со «Стандартом основного общего образования» Работа состоит из пяти  заданий. Все задания требуют записи решения и ответа. Распределение заданий по содержанию и уровню сложности

 

Содержательные линии	Воспроизведени е  знаний	Применение знаний	Интеграция знаний	% соответствия
Арифметическая прогрессия.	№1			20%
Числовые функции	№2		№3	40%
Система неравенств.		№4		20%
Текстовые задачи на составление уравнений.		№5		20%
	40%	40%	20%	100%

 

6.         Время выполнения   На выполнение всей работы отводится 40 минут. 

Дополнительные материалы и оборудование. Линейка, карандаш

 

 

7.         Система  оценивания

 

п/п	Характеристика задания	Проверяемые элементы	Балл за выполнение проверяемого элемента	Балл за выполнение задания
1	Арифметическая прогрессия.	1)      Формула n-го члена арифметической прогрессии. 2)      Формула суммы членов арифметической прогрессии.	1 балл 1 балла	5 баллов

 

Общее количество баллов может быть уменьшено на 1 балл в следующих случаях:

п/п	Характеристика задания	Проверяемые элементы
1	Арифметическая прогрессия.	Формула n-го члена арифметической прогрессии. Формула суммы членов арифметической прогрессии. Решение системы уравнений.
2	Числовые функции	Нахождение области определение функции
3	Числовые функции	Построение графиков «кусочной» функции Свойства числовой функции
4	Решение системы неравенств.	Решение квадратичного неравенства. Решение линейного неравенства.

-          

допущены грамматические ошибки при написании математических терминов;

-           небрежно оформлена работа;

-           небрежно выполнен рисунок к задаче.

8.         Кодификатор

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

5

Решение задачи на составление системы уравнений.

Составление системы уравнений по условию задачи. Решение системы уравнений.

 

 

 

Инструкция для обучающихся по выполнению работы

Итоговая  работа состоит из 5 заданий. Все задания требуют записи решений и ответ.

На выполнение итоговой работы по алгебре отводится 40 минут

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за выполненные задания, суммируются.

Постарайтесь выполнить как можно больше заданий и набрать наибольшее количество баллов.

Общее количество баллов может быть уменьшено на 1 балл в следующих случаях:

-                       допущены грамматические ошибки при написании математических терминов;

-                       небрежно оформлена работа; - небрежно выполнен рисунок к задаче.

 

Желаем успеха!

 

1.        Найти сумму десяти первых членов арифметической прогрессии, если

 

 

2.        Найдите область определения функции  

10 3х х² у. х3 

3.        Решите систему неравенств:.

 

 

4.        . Постройте и прочитайте график функции: 

^ 1 ,если x1; y_x₃

^х⁴, если x1.

 

5.        Диагональ прямоугольника равна 13см, а его площадь равна 60см². Найти периметр прямоугольника.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Контрольно-измерительные материалы  для проведения промежуточной аттестации по геометрии 

7-9 классы

 

Спецификация контрольно- измерительных материалов для проведения промежуточной аттестации по геометрии за курс 7 класса

1.                 Назначение работы: Установление фактического уровня теоретических знаний по предмету, практических умений и навыков, соотнесение этого уровня с требованиями стандарта.

2.                 Общая характеристика структуры и содержания работы: Задания работы ориентированы на учебник «Геометрия 7»(автор .

Л.С.Атанасян,В.Ф.Бутусов ) и составлены в полном соответствии со «Стандартом основного общего образования по математике»В работу включены задания различных типов: 12 заданий, 10 заданий первого уровня сложности, 2 задания второго уровня сложности

3.                 Время выполнения работы – 40 минут. необходимое оборудование - черновик, карандаш, ручка,  линейка, листок с контрольной работой.

4. Система оценивания

Максимальный первичный балл за выполнение всей работы –14 баллов. Задание с кратким ответом считается выполненным, если записанный ответ совпадает с эталоном. Задание с развернутым ответом оценивается экспертом (учителем) с учетом правильности и полноты ответа в соответствии с критериями оценивания. За выполнение ИКР обучающиеся получают оценки по пятибалльной шкале.

Задания 1-10	1 балл	Получен верный ответ
Задания 11-12	2 балла	(ход решения верный, все его шаги выполнены правильно, получен верный ответ);
	1 балл	(ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена однавычислительная ошибка)
	0 баллов	(другие       случаи,       не      соответствующие          указанным критериям).

Шкала перевода полученных баллов в отметку :

14 – 11 баллов : отметка «отлично»

10 – 9 баллов : отметка «хорошо»;

8 – 7 баллов : отметка «удовлетворительно»;

      Менее 7 баллов : отметка «неудовлетворительно».

5. Кодификатор

	Содержание	Контролируемое знание/умение
1	Измерение отрезков.	Уметь применять свойство измерения отрезков при решении задач.
2	Сравнение отрезков.	Уметь применять свойство сравнения отрезков при решении задач.
3	Периметр треугольника.	Знать определение периметра и уметь вычислять периметр плоских фигур.
4	Сумма углов треугольника.	Уметь применять теорему о сумме углов треугольника при решении задач.
5	Соотношения между сторонами и углами в треугольнике.	Уметь составлять уравнение, применять свойство сравнения углов и сторон, решать задачи.
6	Неравенство треугольника.	Уметь применять неравенство треугольника при решении задач.
7	Смежные углы.	Уметь применять теорему о смежных углах к решению задач.
8	Вертикальные углы.	Уметь применять теорему о вертикальных углах к решению задач.
9	Признаки параллельности прямых.	Знать признаки параллельности.
10	Соотношения между сторонами и углами в прямоугольном треугольнике.	Уметь применять соотношения между сторонами и углами в треугольнике при решении задач.
11	Сумма углов треугольника.	Уметь составлять уравнение на сумму углов треугольника.
12	Соотношения между сторонами и углами в прямоугольном треугольнике.	Уметь применять теорему о стороне прямоугольного треугольника, лежащей против угла в 30 градусов.

 

 

Вариант1

Инструкция для обучающихся по выполнению работы: 12 заданий, 10 заданий первого уровня сложности, 2 задания второго уровня сложности, рекомендуем сначала выполнять задания первой части. Начать советуем с тех заданий, которые вызывают у вас меньше затруднений, затем переходите к следующим заданиям. Все необходимые           вычисления    выполняйте   в          черновике,             записи            в          черновике       не учитываются при оценивании работы. Рекомендуем внимательно читать условие и проводить проверку полученного ответа. Ответ к заданиям первой части заносим в таблицу в виде числа. Решение к заданиям второй части записывайте в виде развернутого ответа с подробными пояснениями. Текст задания переписывать не надо, необходимо указать его номер Часть  1.

1.            Длина отрезка АВ равна 4,3 см, длина отрезка СД в 5 раза больше.  Найти сумму длин этих отрезков.

2.            Точка С  лежит на отрезке  АВ. Сравните длины отрезков

А)  АС >АВ               Б) СВ < АВ                 В)АВ <СВ                     Г) АВ =АС

3.            Найдите периметр треугольника  АВС, если АВ равно 8 см, АС на 1см больше АВ, а отрезок ВС в 2 раза больше АВ.

4.            В треугольнике МКЕ угол М равен 41°, угол К на 52° больше. Вычислите угол Е.

5.            Углы треугольника АВС относятся как 5:3 :1. Вычислите самый большой угол этого треугольника.

6.            Найдите самый маленький угол в треугольнике АВС, если АВ< АС<ВС.

7.            Один из смежных углов на 48° больше другого. Найдите меньший угол.

8.            Сумма вертикальных углов равна 136°. Вычислите один из вертикальных углов.

 

9.            Выберите  верное утверждение.  Если две параллельные прямые пересечены секущей, то

А) накрест лежащие углы в сумме дают 180 °

Б) смежные углы равны

В) соответственные углы равны

Г) односторонние углы равны

10.       В прямоугольном треугольнике АВС  угол В равен 90 °, угол С равен

45 °. Сравните стороны треугольника

 

Часть 2. 11. Периметр равнобедренного треугольника равен 26см, разность двух сторон равна 5 см, а один из его внешних углов – острый. Найдите стороны треугольника.

 

 

Вариант 2.

Инструкция для обучающихся по выполнению работы: 12 заданий, 10 заданий первого уровня сложности, 2 задания второго уровня сложности, рекомендуем сначала выполнять задания первой части. Начать советуем с тех заданий, которые вызывают у вас меньше затруднений, затем переходите к следующим заданиям. Все необходимые вычисления выполняйте в черновике, записи в черновике не учитываются при оценивании работы. Рекомендуем внимательно читать условие и проводить проверку полученного ответа. Ответ к заданиям первой части заносим в таблицу в виде числа. Решение к заданиям второй части записывайте в виде развернутого ответа с подробными пояснениями. Текст задания переписывать не надо, необходимо указать его номер.

Часть 1.

1.Длина отрезка ВС равна 3,8 см, длина отрезка АД в 6 раз больше. Найти сумму длин этих отрезков.

2.Точка В лежит на отрезке АС. Сравните длины отрезков:

А) АС  >  АВ       Б) СВ  <  АВ       В)  АВ <    СВ     Г)  АВ= АС

3.                       Найдите периметр треугольника АВС , если АВ равно 7 см, АС на 1 см больше АВ, а отрезок ВС в 2 раза больше АВ.               

4.                       В треугольнике МКЕ угол К равен 42°,  угол М на 57 ° больше. Вычислите       

                  угол Е.

5 . Углы треугольника АВС относятся как 4:3 :2.  Вычислите самый большой угол этого треугольника.

6.Найдите самый маленький угол в треугольнике АВС, если АВ< АС <ВС.

7.     Один из смежных углов на 54° больше другого. Найдите больший  угол.

8.     Сумма вертикальных углов равна 132°. Вычислите один из вертикальных углов.

 

9.     Выберите  верное утверждение.  Если две параллельные прямые пересечены секущей, то

А) накрест лежащие углы равны

Б) смежные углы равны

В) соответственные углыв сумме дают 180 °

Г) односторонние углы равны

10. В прямоугольном треугольнике АВС  угол А  равен 90 °, угол В равен 42°. Сравните стороны треугольника

Часть 2.

11. Один из углов треугольника в два раза больше другого угла и  на 30 ° больше  третьего угла этого треугольника. Вычислите углы треугольника.

 

 

Демонстрационный вариант 

итоговой контрольной работы по геометрии за курс 7 класса.

1.Длина отрезка ВС равна 8,5 см, длина отрезка АД в 7 раз больше. Найти сумму длин этих отрезков.

2.Точка В лежит на отрезке АС. Сравните длины отрезков:

А) АС  >  АВ       Б) СВ  <  АВ       В)  АВ <    СВ     Г)  АВ= АС

3. Найдите периметр треугольника АВС , если АВ равно 9 см, АС на 3 см больше АВ, а отрезок ВС в 3 раза больше АВ.               

4. В треугольнике МКЕ угол К равен 52°,  угол М на 47 ° больше. Вычислите                          угол Е.

5 . Углы треугольника АВС относятся как 7:5 :6.  Вычислите самый большой угол этого треугольника.

6.  Найдите самый маленький угол в треугольнике АВС, если АВ< АС <ВС.

7.  Один из смежных углов на 74° больше другого. Найдите больший  угол.

8.Сумма вертикальных углов равна 264°. Вычислите один из вертикальных углов.

 

9.        Выберите  верное утверждение.  Если две параллельные прямые пересечены секущей, то

А) накрест лежащие  углы в сумме дают 180 °

Б) смежные углы равны

В) соответственные углы равны

Г) односторонние углы равны

10.    В прямоугольном треугольнике АВС  угол А  равен 90 °, угол В равен 68°. Сравните стороны треугольника

 

Часть 2.

 

11.    Один из углов треугольника в два раза больше другого угла и  на 30 ° больше  третьего угла этого треугольника. Вычислите углы треугольника.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Спецификация контрольно- измерительных материалов для проведения промежуточной аттестации по геометрии за курс 8 класса

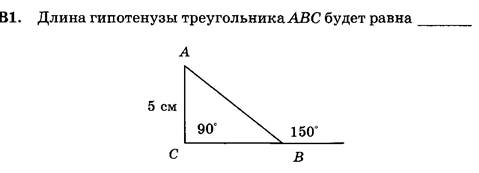
1.                 Назначение работы: Установление фактического уровня теоретических знаний по предмету, практических умений и навыков, соотнесение этого уровня с требованиями стандарта.

2.                 Общая характеристика структуры и содержания работы: Задания работы ориентированы на учебник «Геометрия 8»(автор .

Л.С.Атанасян,В.Ф.Бутусов ) и составлены в полном соответствии со «Стандартом основного общего образования по математике»В работу включены задания различных типов: 12 заданий, 10 заданий первого уровня сложности, 2 задания второго уровня сложности

3.                 Время выполнения работы – 40 минут. необходимое оборудование - черновик, карандаш, ручка,  линейка, листок с контрольной работой.

Задания 1-10	1 балл	Получен верный ответ
Задания 11-12	2 балла	(ход решения верный, все его шаги выполнены правильно, получен верный ответ);
	1 балл	(ход решения верный, все его шаги выполнены правильно, но даны неполные объяснения или допущена одна  вычислительная ошибка)
	0 баллов	(другие случаи, не соответствующие указанным критериям).

4.                 Система оценивания Максимальный первичный балл за выполнение всей работы –14 баллов. Задание с кратким ответом считается выполненным, если записанный ответ совпадает с эталоном. Задание с развернутым ответом оценивается экспертом (учителем) с учетом правильности и полноты ответа в соответствии с критериями оценивания. За выполнение ИКР обучающиеся получают оценки по пятибалльной шкале.

 

 

 

Шкала перевода полученных баллов в отметку :

14 – 11 баллов : отметка «отлично»;

10 – 9 баллов : отметка «хорошо»;

8 – 7 баллов : отметка «удовлетворительно»;

Менее 7 баллов : отметка «неудовлетворительно».

	Содержание	Контролируемое знание/умение
1	Площадь прямоугольника.	Уметь применять формулу для вычисления площади прямоугольника.
2	Площадь параллелограмма.	Уметь применять формулу для вычисления площади параллелограмма.
3	Сумма углов четырехугольника.	Уметь находить углы ромба.
4	Площадь треугольника.	Уметь применять теорему Пифагора, находить площадь треугольника.
5	Градусная мера дуги окружности.	Уметь находить градусную меру дуги окружности.
6	Свойства четырехугольника.	Знать свойства четырехугольника.
7	Свойства диагоналей ромба.	Уметь применять свойства диагоналей ромба  к решению задач.
8	Площадь квадрата.	Знать формулу площади квадрата.
9	Свойство прямоугольного треугольника.	Знать свойство катета в прямоугольном треугольнике лежащего против угла 30 градусов.
10	Соотношения между сторонами и углами в прямоугольном треугольнике.	Знать определение синуса и косинуса острого угла прямоугольного треугольника.
11	Нахождение стороны квадрата через диагональ.	Уметь применять теорему Пифагора при нахождении стороны квадрата через диагональ.
12	Соотношения между сторонами и углами треугольника.	Уметь применять признаки подобия треугольников при решении задач.

5. Кодификатор

 

Вариант1

Инструкция для обучающихся по выполнению работы: 12 заданий, 10 заданий первого уровня сложности, 2 задания второго уровня сложности, рекомендуем сначала выполнять задания первой части. Начать советуем с тех заданий, которые вызывают у вас меньше затруднений, затем переходите к следующим заданиям. Все необходимые вычисления выполняйте в черновике, записи в черновике не учитываются при оценивании работы. Рекомендуем внимательно читать условие и проводить проверку полученного ответа. Ответ к заданиям первой части заносим в таблицу в виде числа. Решение к заданиям второй части записывайте в виде развернутого ответа с подробными пояснениями. Текст задания переписывать не надо, необходимо указать его номер

1.        Площадь прямоугольника АВСD равна 15. Найдите  сторону ВС прямоугольника, если известно, что АВ = 5.

2.        В параллелограмме две стороны 12 и 16 см, а один из углов 150°. Найдите площадь параллелограмма. 3.  В ромбе АВСD проведена диагональ АС. Найдите  угол АВС, если известно, что угол АСD  равен 35°.

4. Найдите площадь равнобедренного треугольника со сторонами 10см, 10см и 12 см. 5. По данным рисунка найдите градусную меру      дуги Х.                                                                                                          

          

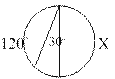
6.  Укажите, какие из перечисленных ниже утверждений верны:

1)  Если диагонали параллелограмма  равны, то он прямоугольник.

2)  Если      противоположные    стороны          четырехугольника    попарно    равны,            то        он параллелограмм.

3)  Если диагонали параллелограмма  перпендикулярны, то он ромб.

4)  Диагонали прямоугольника являются биссектрисами его углов.

7.      Сторона ромба равна 5 , а одна из его диагоналей равна 6 . Найти вторую диагональ.

8.      Площадь квадрата со стороной 5 2 равна 

9.      Катет прямоугольного треугольника, противолежащий углу в 30⁰,  равен 16см. Найдите гипотенузу.

10.  В прямоугольном треугольнике  АВС катеты АС=3см, ВС=4см гипотенуза равна 5см. Найдите синус угла А.

Часть II

11.  Квадрат вписан в окружность диаметра 8. Найти периметр квадрата.

12.  В трапеции ABCD (ВC || AD) ВС = 9 см, AD = 16 см,  BD = 18 см. Точка О – точка пересечения AC и BD. Найдите ОВ.

 

                                                   Вариант 2.

Часть I. 

1.  Площадь прямоугольника АВСD равна 18. Найдите  сторону АВ прямоугольника, если известно, что ВС = 6.

2 В параллелограмме АВСД   АВ=8 см, АД=10 см, ВАД =30°. Найдите площадь параллелограмма.

3.    В ромбе АВСD проведена диагональ АС. Найдите  угол АDС, если известно, что угол АСB  равен 35°.

4.    В равнобедренном треугольнике боковая сторона равна 13 см, а высота, проведенная к основанию, 5 см. Найдите площадь этого треугольника.

5.    По данным рисунка найдите градусную меру      дуги Х.                                                                                                                

                                  40˚        

6.    Укажите, какие из перечисленных ниже утверждений верны:

1)  Если диагонали четырехугольника равны, то он прямоугольник.

2)  Если      противоположные    стороны          четырехугольника    попарно    равны,            то        он параллелограмм.

3)  Если диагонали четырехугольника перпендикулярны, то он ромб.

4)  Диагонали прямоугольника являются биссектрисами его углов.

7.      Сторона ромба равна 5, а одна из его диагоналей равна 8..Найти вторую диагональ.

8.      Площадь квадрата со стороной  3 2 равна 

9.      Катет прямоугольного треугольника, противолежащий углу в 30⁰,  равен 12 см. Найдите гипотенузу.

10.  В прямоугольном треугольнике   АВС катеты АС=6см, ВС=8см гипотенуза равна 10см. Найдите косинус угла А.

Часть II

11.  Квадрат вписан в окружность диаметра 4. Найти периметр квадрата.

12.  В △MPK     МР = 24 см,   DE || МР ,  причем D € МК, Е € РК.    Найти МК,   если DM = 6 см, DE = 20 см. 

Демонстрационный вариант 

итоговой контрольной работы по геометрии за курс 8 класса.

Часть I. 

1.  Площадь прямоугольника АВСD равна 48. Найдите  сторону АВ прямоугольника, если известно, что ВС = 8.

2 В параллелограмме АВСД   АВ=18 см, АД=12 см, ВАД =30°. Найдите площадь параллелограмма.

3.    В ромбе АВСD проведена диагональ АС. Найдите  угол АDС, если известно, что угол АСB  равен 42°.

4.    В равнобедренном треугольнике боковая сторона равна 17 см, а высота, проведенная к основанию,15 см. Найдите площадь этого треугольника.

5.    По данным рисунка найдите градусную меру  

                         дуги Х.                                                                                                                       

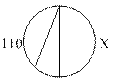
                                  _40˚            

6.    Укажите, какие из перечисленных ниже утверждений верны:

1)  Если диагонали четырехугольника равны, то он прямоугольник.

2)  Если  стороны четырехугольника попарно равны, то он параллелограмм.

3)  Если диагонали четырехугольника перпендикулярны, то он ромб.

4)  Диагонали прямоугольника являются биссектрисами его углов.

7.      Сторона ромба равна 10, а одна из его диагоналей равна 16..Найти вторую диагональ.

8.      Площадь квадрата со стороной  4 2 равна 

9.      Катет прямоугольного треугольника, противолежащий углу в 30⁰,  равен 24 см. Найдите гипотенузу.

10.  В прямоугольном треугольнике   АВС катеты АС=12см, ВС=16см гипотенуза равна 20см. Найдите косинус угла А.

Часть II

11.  Квадрат вписан в окружность диаметра 12. Найти периметр квадрата.

12.  В △MPK     МР = 12 см,   DE || МР ,  причем D € МК, Е € РК.    Найти МК,   если DM = 3 см, DE = 10 см. 

 

 

 

 

 

 

 

 

 

 

Спецификация контрольно- измерительных материалов для проведения промежуточной аттестации по геометрии за курс 9 класса

 

1. Назначение работы: оценить уровень общеобразовательной подготовки по геометрии обучающихся  9 класса 2. Общая характеристика структуры и содержания работы.

Задания работы ориентированы на учебник «Геометрия 7-9»(автор .

Л.С.Атанасян, В.Ф.Бутусов ) и составлены в полном соответствии со «Стандартом основного общего образования» Работа состоит из двух частей.

Часть 1 направлена на проверку овладения содержанием курса на уровне базовой подготовки. Эта часть содержит 10 заданий, предусматривающих две формы ответа: задания с выбором ответа из четырех предложенных вариантов, с кратким ответом.

При выполнении заданий первой части учащиеся должны продемонстрировать определенную системность знаний и широту представлений по курсу геометрии 7-9 класса.

Часть 2 направлена на проверку владения материалом на повышенных уровнях. Эта часть содержит 2 задания (№ 11- № 13) разного уровня сложности, требующих развернутого ответа (с записью решения). 

3. Время выполнения работы – 45 минут

необходимое оборудование - черновик, карандаш, ручка,  линейка, листок с контрольной работой.

4. Критерии оценивания результатов выполнения работы.

Для оценивания результатов выполнения работ учащимися применяются два количественных показателя: традиционные отметки «2», «3», «4» или «5» и общий балл за верно выполненные задания первой и второй частей.

Общий балл формируется путем подсчета общего количества баллов, полученных учащимися за выполнение первой и второй частей работы. В итоге за первую часть можно получить 10 баллов, за вторую – 6  баллов, в целом за работу – 16 баллов.

Система формирования общего балла

задания	Максимальное количество баллов за выполнение заданий части 1	Максимальное количество баллов за выполнение заданий части 2			Общий балл
	Задания 1-10	11	12	13
баллы	10	2	2	2	16

 

   Правильное выполнение каждого задания 1 части работы оценивается 1 баллом, если ответ неверный или отсутствует – 0 баллов.

Учащийся, демонстрирующий умение решить ту или иную задачу второй части работы, получает установленный балл, или балл, на 1 меньше установленного (в случае, если в решении допущена ошибка, не носящая принципиального характера и не влияющая на общую правильность хода решения).

 

 

Схема перевода рейтинга в отметку.

 

Отметка по пятибалльной шкале	«2»	«3»	«4»	«5»
Общий балл	0-7 баллов	8-12 баллов	13-14 баллов	15-16  баллов

 

5. Кодификатор 

№ задания	Проверяемое умение
1	Знание свойства смежных углов
2	Знание признаков равенства треугольников
3	Знание уравнения окружности
4	Знание свойств центрального и вписанного угла
5	Умение определять верные высказывания из предложенных вариантов
6	Знание свойств равнобедренного треугольника
7	Умение находить площади фигур
8	Знание и умение применять теорему Пифагора
9	Знание определения и свойств описанной окружности
10	Умение выполнять преобразования векторов через координаты
11	Знание и умение применять теорему косинусов
12	Знание и умение применять теорему синусов
13	Умение применять признаки подобия треугольников

 

 

                           

Инструкция для обучающихся по выполнению работы: 13 заданий, 10 заданий первого уровня сложности, 3 задания второго уровня сложности, рекомендуем сначала выполнять задания первой части. Начать советуем с тех заданий, которые вызывают у вас меньше затруднений, затем переходите к следующим заданиям. Все необходимые вычисления выполняйте в черновике, записи в черновике не учитываются при оценивании работы. Рекомендуем внимательно читать условие и проводить проверку полученного ответа. Ответ к заданиям первой части заносим в таблицу в виде числа. Решение к заданиям второй части записывайте в виде развернутого ответа с подробными пояснениями. Текст задания переписывать не надо, необходимо указать его номер

 1. Один из смежных углов на 40˚ больше другого.                     Чему равны эти углы?

 

А. 90˚ и 50˚

В. 40˚ и 80˚

С. 110˚ и 70˚

D.  100˚ и 140

 

2. Какие из элементов должны быть равны у △АВС и △А₁В₁С₁, чтобы они были равны по стороне и двум        прилежащим углам?          

                                               А        А₁  

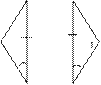                                                                                                       В                          В                                                С          С₁

 

А.  ∠А = ∠А₁

                      В.  ∠В = ∠В₁               

                      С.   ВС =  В1С                                                                                                                 

   D.   АВ = А₁ В₁

 

 

3.  Запишите уравнение окружности с центром  в точке  С (3; -2) и радиусом 5.

 

А.(х -3)² + (у + 2)² = 25

В. (х +3)² + (у - 2)² = 25 С. (х -3)² + (у - 2)² = 5

D. (х -3)² * (у + 2)² = 25

 

 

4. По данным рисунка найдите градусную меру  

                         дуги Х.                                                                                                                       

                                                                    

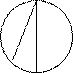120˚                    Х

 

            _30˚  

 

 

 

 

А. 210˚

В. 225˚

С. 180˚

D. 150˚   

 

5. Какие из высказываний верны:

1)  Если диагонали параллелограмма равны, то он прямоугольник.

2)  Если противоположные стороны четырехугольника попарно равны, то он параллелограмм.

3)  Если диагонали параллелограмма перпендикулярны, то он ромб. 4) Диагонали прямоугольника являются биссектрисами его углов.

 

А. 1, 3             

В. 3, 4          

С. 2         

D. 1, 2

 

 

6.            В равнобедренном треугольнике угол при основании равен 70˚.  Найдите угол при вершине. Ответ:__________________

 

7.            По данным рисунка найти площадь параллелограмма.

 

Ответ:_______________________

 

8.            Стороны прямоугольника равны 6 м и 8 м. 

Найдите диагональ прямоугольника

Ответ:___________________

                                        

                                             

9.            В квадрат со стороной 10 см вписана окружность.  Найдите ее радиус.

Ответ:_______________________

10.        Известно,       что      вектор            _a^r {3; -5},

 

r вектор     { b 0; -4}. 

                                                                                   r              r

                            Найдите координаты вектора 2    – ^a ½           b

Ответ:_____________________________

 

Часть 2

11.  (2 балла)  По данным рисунка найдите сторону ВС.

 

        

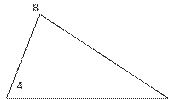
12.  (2 балла)  По данным рисунка найдите сторону ВС. 

 

 

        

 

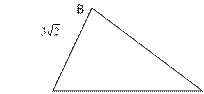
13.  (2              балла)  В трапеции ^{60                        45} ABCD (ВC || AD) ВС = 9 см, AD = 16 см,  BD = 18 см. Точка О – точка пересечения AC и BD. Найдите ОВ.