КОМБИНАТОРИКА РАЗБИЕНИЙ. ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача 5.1. Восемь разных книг нужно расставить по трем полкам так, чтобы на одной полке оказалось 2 книги, а на двух других - по 3 книги. Сколькими способами это можно сделать?

Поскольку в данной формулировке полки не различимы, то речь идет о неупорядоченном разбиении множества книг на три подмножества мощности 2, 3 и 3. Параметры m₁ = 1, m₂ = 2, поэтому число разных способов расставить книги так, как это требуется в условии задачи, равно

 = 280.

Приведенные выше примеры показывают, как важно для решения задачи выбрать наиболее подходящую комбинаторную схему, правильно определить, какие именно комбинаторные операции требуется выполнить над исходным множеством. Иногда формулировка задачи допускает неоднозначное понимание того, какие результаты комбинаторной операции считаются одинаковыми, а какие – разными. В таких случаях нужно самостоятельно сделать необходимые уточнения.[24]

Задача 5.2. одинаковых шариков случайным образом рассыпаются по 4 лункам (в одну лунку может поместиться любое число шаров). Сколько существует различных способов распределения 7 шариков по 4 лункам?[11]

Решение. Мы имеем 7 шариков, которые распределяем по 4 лункам (лунки могут быть пустые), т. е. это соответствует формуле о разбиениях    = kⁿ, число способов равно 4⁷ = 16348.

Ответ: 16348.

Задача 5.3. Стадион имеет 4 входа. Сколькими способами болельщик может войти на стадион в один вход, а выйти через другой?[12]

Решение. Воспользуемся формулой о разбиениях (3), число способов равно  = 12.

Ответ: 12.

Задача 5.4. При игре в домино 4 игрока делят поровну 28 костей. Сколькими способами они могут это сделать? [11]

Решение. Это задача о разделе 28 костей между 4 игроками по 7 костей.

Используя формулу для числа способов такого раздела (3)

имеем   47·10¹⁵.

Ответ: 47·10¹⁵.

Задача 5.5. Сколькими способами можно разместить 4 книги на полке?[16]

Решение. Воспользуемся формулой о разбиениях n!, число способов равно 4! = 1·2·3·4 = 24

Ответ: 24.

Задача 5.6. Сколькими способами можно поставить в ряд 6 человек для выполнения их группового портрета? Сколькими способами можно это сделать, если поставить трех человек в переднем ряду и трех во втором?[12]

Решение. Воспользуемся формулой о разбиениях n!, число способов равно 6! = 1·2·3·4·5·6 = 720

Ответ: 720.

Задача 5.7. Сколько различных «слов» можно составить, переставляя буквы слова «лодка»?[12]

Решение. Слово «лодка» состоит из 5 различных букв. Значит можно воспользоваться формулой n!, число различных «слов» будет 5! = 1·2·3·4·5 = = 120.

Ответ: 120.

Задача 5.8. Сколько различных «слов» можно составить, переставляя буквы слова «математика»?[20]

Решение. Слово «математика» состоит из 10 повторяющихся букв: 3 буквы «а», 2 буквы «м», 2 буквы «т». Значит можно воспользоваться формулой (3), число различных «слов» будет  = = 151200.

Ответ: 151200.

Задача 5.9. Сколько различных слов можно составить, переставляя буквы слова «комбинаторика»?[11]

Решение. Слово «комбинаторика» состоит из 13 повторяющихся букв: 2 буквы «к», 2 буквы «о», 2 буквы «и», 2 буквы «а». Значит можно воспользоваться формулой (3), число различных «слов» будет  = = 389188800.

Ответ: 389188800.

Задача 5.10. В классе изучают 10 предметов. В понедельник 6 уроков, причем все уроки разные. Сколькими способами можно составить расписание на понедельник?[13]

Решение. Воспользуемся формулой о разбиениях  = , число способов равно  =  =  =  = 151200.

Ответ: 151200.

Задача 5.11. Сколькими способами можно выбрать трех делегатов на студенческую конференцию из группы в 20 человек?[21]

Решение. Воспользуемся формулой  = , число способов равно  =  =  =  =1140.

Ответ: 1140.

Задача 5.12. Сколькими способами можно расставить 40 различных книг по шести полкам так, чтобы не было пустых полок, если на полку помещаются все 40 книг?

Решение. В задаче опять важно, на какую полку, и в каком порядке расставляются книги, но теперь не должно быть пустых полок. Поэтому искомое число расстановок  .[10]

Задача 5.13. Рассеянный почтальон должен разнести
12 писем по 12 адресам. Сколькими способами он может разложить письма по почтовым ящикам так, чтобы

а) ни один адресат не получил адресованное ему письмо;

б) ровно 5 человек получили адресованные им письма;

в) хоть один адресат получил адресованное ему письмо;

г) ровно один адресат получил адресованное ему письмо?

Решение. а) В силу предыдущей задачи искомое число способов .

б) Согласно формуле (1.6.12) искомое число способов равно .

в) Всего  способов раскладки писем по ящикам, из них в  случаях ни один адресат не получит адресованное ему письмо. Поэтому искомое число способов .

г) Очевидно, что такой ситуации быть не может.

Задача 5.14 (задача о беспорядках). Имеется  различных предметов  и  различных ячеек . Требуется разместить предметы по ячейкам так, чтобы никакой предмет  не попал в ячейку . Сколько существует таких способов размещения?

Решение. Примем за  множество всевозможных раскладок предметов по ячейкам. Число таких раскладок равно числу перестановок из  элементов, т.е.  Условимся, что свойство  означает: элемент  находится в ячейке , . Тогда  – число раскладок, при которых элемент  находится в ячейке  (), а  – число раскладок, при которых никакой предмет  не попал в ячейку . По формуле .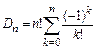

Задача 5.15. Контрольную работу по дискретной математике, содержащую три задачи, писали 105 студентов III курса. Первую задачу решили 70 человек, вторую – 59, а третью – 62. С первой и второй задачами справились – 39 студентов, со второй и третьей – 32, с первой и третьей – 41. Шесть человек не решили ни одной задачи. Сколько студентов полностью справились с контрольной работой?

Решение. Множество студентов примем за , а за свойства  – решение студентом первой, второй и третьей задачи соответственно. Тогда , , , , , , . Подставляя эти значения в формулу (1.6.5), получим

6 = 105 – (70 + 59 + 62) + (39 + 32 + 41) – .

Отсюда .

Задача 5.16. Имеются цветы трех видов: 10 васильков, 15 незабудок, 12 ромашек. Требуется разложить их на 2 букета.[11]

Решение. Васильки на 2 букета можно разложить 11 способами, незабудки - 16, ромашки - 13 способами. Поскольку расклад каждого вида цветов выполняется независимо, то общее число вариантов расклада будет: 11·16·13.

Задача 5.17. Из группы в 15 человек нужно отобрать бригаду, в которую должно входить не менее 5 человек. Сколько имеется вариантов выбора?

Решение. Подсчитаем число неблагоприятных комбинаций выбора, т. е. составим варианты бригад из 1, 2, 3, 4 человек. Их количество равно:

А общее количество бригад равно 2¹⁵ – 1. Разность дает число благо­приятных комбинаций.[17]

Задача 5.18. Трое мальчиков собрали 40 яблок. Сколько имеется способов раздела яблок между ними?

Решение. Напишем 40 единиц и 2 нуля, выполняющих как и ранее функции разделителя, и затем начнем их переставлять всеми возможными способами. Каждой перестановке будет соответствовать некоторый способ раздела 40 яблок на 3 кучки. Каждому способу раздела будет соответствовать некоторый код, содержащий 40 единиц и 2 нуля. Поэтому количество способов раздела:

Р(40,2) = 42!/(2!40!) = 861.

Задача 5.19. В ящике находится 15 деталей. Сколькими способами можно взять 4 детали?

Решение: В задаче речь идёт о выборке из 4 деталей, в которой не имеет значения их «дальнейшая судьба» – грубо говоря, «просто выбрали 4 штуки и всё». Таким образом, у нас имеют место сочетания деталей. Считаем их количество:

2365 способами можно взять 4 детали из ящика.

Ответ: 1365 способами

Задача 5.20. Восемь разных книг нужно расставить по трем полкам так, чтобы на верхней полке оказалась 1 книга, на средней полке - 3 книги, на нижней полке - 4 книги. Сколькими способами это можно сделать?

В данном примере множество из восьми книг разбивается на три непересекающихся подмножества мощности 1, 3 и 4. Согласно формуле (3) количество различных вариантов выполнить такое разбиение равно

 = 280.