
Министерство образования, науки и молодежи Республики Крым Государственное бюджетное профессиональное образовательное учреждение Республики Крым
«Феодосийский политехнический техникум»
Утверждаю:
Заместитель директора по учебной работе О.Г. Сердюкова
«____» _____ 2016г.
Комплект оценочных средств по междисциплинарному курсу
МДК 01.02 Математический аппарат для построения компьютерных сетей
ПМ.01Участие в проектировании сетевой инфраструктуры
в рамках программы подготовки специалистов среднего звена
по специальности среднего профессионального образования
09.02.02 Компьютерные сети
Форма проведения оценочной процедуры: экзамен
Феодосия, 2016
Организация - разработчик: Государственное бюджетное профессиональное образовательное учреждение Республики Крым «Феодосийский политехнический техникум»
Разработчики: преподаватель Г.А. Кузьмич
Комплект оценочных средств по МДК 01.02 Математический аппарат для построения компьютерных сетей рассмотрен и одобрен на заседании цикловой комиссии компьютерных дисциплин Протокол № ___ от_______ 2016 г.
Председатель ЦК ____________ Т.Н. Дворянова
Комплект оценочных средств по МДК 01.02 Математический аппарат для построения компьютерных сетей рассмотрен и одобрен на заседании методического совета Протокол № ___ от_______ 2016 г.
Председатель методического совета ____________ О.Г. Сердюкова
Старший методист ____________ Т.Н. Старовойтова
1.1 Общие положения
Результатом освоения междисциплинарного курса является готовность обучающегося к выполнению вида профессиональной деятельности Математический аппарат для построения компьютерных сетей. Основой такой готовности является форсированность у обучающихся всех профессиональных компетенций, входящих в состав профессионального модуля. Общие компетенции формируются в процессе освоения ОПОП в целом, поэтому по результатам освоения профессионального модуля возможно оценивание положительной динамики их формирования.
Формой промежуточной аттестации по междисциплинарному курсу является дифференцированный зачет (1 семестр), экзамен (2семестр).
1.2 Результаты освоения междисциплинарного курса, подлежащие проверке
Таблица 1
|
Предмет(ы) оценивания |
Показатели оценки |
Критерии оценки |
Тип задания |
|
У.2 выбирать сетевые топологии; У.3 рассчитывать основные параметры локальной сети; У.5 применять алгоритмы поиска кратчайшего пути; У.6 планировать структуру сети с помощью графа с оптимальным расположением узлов; У.7 использовать математический аппарат теории графов; У.12 использовать техническую литературу и информационно- справочные системы для замены (поиска аналогов) устаревшего оборудования; З.1 сетевые топологии; З.10 вероятностные и стохастические процессы, элементы теории массового обслуживания, основные соотношения теории |
- определение и описание сетевых топологий для конкретной задачи; - дифференцирование и распознавание основных параметров локальной сети; - определение и разработка алгоритма поиска кратчайшего пути для оптимизации локальной сети; - разрабатывать структуры сети с оптимальным расположением узлов с помощью математического аппарата теории графов; - систематизирование знаний, полученных из технической и информационносправочной литературы для поиска аналогов устаревшего оборудования; - определение и сопоставление |
- сетевая топология выбрана, верно, и оптимальна; - правильно идентифицирована и распознана локальная сеть; - создан оптимальный граф с расположением узлов с помощью математического аппарата теории графов и систем массового обслуживания, теории очередей, вероятностных и стохастических процессов; - умение быстро и верно искать информацию о разных параметрах сети и сетевых топологий; - умение находить решение проблем |
- простые вопросы с коротким ответом; - решение расчетных, ситуационных задач; - фронтальный опрос; - самостоятельная работа; - практические работы; - теоретические вопросы и практические задания экзаменационных билетов по МДК 01.02;
|
|
Предмет(ы) оценивания |
Показатели оценки |
Критерии оценки |
Тип задания |
|
очередей, основные понятия теории графов; З.11 алгоритмы поиска кратчайшего пути; З.12 основные проблемы синтеза графов атак; З.13 построение адекватной модели; |
вероятностных и стохастических процессов, элементов теории массового обслуживания, основные соотношения теории очередей; - оценка и управление синтезом графа атак в локальной сети; - анализировать и дифференцировать построенные или имеющиеся модели локальной сети, или разработка и оценка адекватной модели; |
синтеза графов атак; - правильная идентификация построенной локальной сети и умение находить и править ее основные параметры для наиболее оптимальной ее работы; |
|
|
ПК 1.3. Обеспечивать защиту информации в сети с использованием программно-аппаратных средств. ПК 1.3. Обеспечивать защиту информации в сети с использованием программно-аппаратных средств. ОК 1. Понимать сущность и социальную значимость своей будущей профессии, проявлять к ней устойчивый интерес. ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество. ОК 3. Принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность. ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного |
- применение математического аппарата теории графов в решении задач; - навыки в применении алгоритма Краскала; - поиск кратчайшего пути в графе при помощи алгоритма Дейкстры; - обоснованный выбор варианта поиска пути: подстановки, удобная форма записи, перебор вершин по алфавиту, перебор всех путей с начала, графический; - решение задач системам массового обслуживания; - знание сложных стохастических моделей, овладение современным математическим аппаратом для дальнейшего использования в разнообразных приложениях; - определение числовых характеристик случайной величины; - правила преобразования и |
- умение правильно применять математический аппарат теории графов для решения задач; - применение кратчайшего пути в графе и алгоритма Дейкстры для построения сети; - обоснованный выбор правильного и оптимального варианта поиска пути при моделировании или создания сети; -умение анализировать и дифференцировать сложные стохастические модели, числовые характеристики случайной величины, типовых распределений, характеристик систем массового обслуживания с |
- решение ситуационных, учебнопрофессиональных задач; - теоретические вопросы и практические задания экзаменационных билетов по МДК 01.02;
|
|
Предмет(ы) оценивания |
Показатели оценки |
Критерии оценки |
Тип задания |
|
выполнения профессиональных задач, профессионального и личностного развития. ОК 5. Использовать информационнокоммуникационные технологии в профессиональной деятельности. ОК 6. Работать в коллективе и в команде, эффективно общаться с коллегами, руководством, потребителями. ОК 7. Брать на себя ответственность за работу членов команды (подчиненных), за результат выполнения заданий. ОК 8. Самостоятельно определять задачи профессионального и личностного развития, заниматься самообразованием, осознанно плани- ровать повышение квалификации. ОК 9. Ориентироваться в условиях частой смены технологий в профессиональной деятельности.
|
вычисления типовых распределений; - определения характеристик системы массового обслуживания; - систематизирование знаний, полученных из литературы для решения проблем поиска оптимальной системы сети; - оценка и критика построенной локальной сети и защита информации с использованием программно-аппаратных средств.
|
теорией очередей и овладение современным математическим аппаратом для дальнейшего использования в разнообразных приложениях; - верна критика и оценка локальной сети и умение защищать информацию с использованием программноаппаратных средств. |
|
1.3 Система оценки освоения программы междисциплинарного курса
Оценка "отлично" выставляется студенту, если он глубоко и прочно усвоил программный материал, исчерпывающе, последовательно, четко и логически стройно его излагает, умеет тесно увязывать теорию с практикой, правильно обосновывает принятое решение, владеет разносторонними навыками и приемами выполнения практических задач, умеет собирать, систематизировать, анализировать и грамотно использовать практический материал для иллюстраций теоретических положений, умеет самостоятельно решать задачу на основе изученных методов, приемов, технологий; умеет создавать и применять документы, связанные с профессиональной деятельностью; умеет анализировать современное состояние отрасли, науки и техники; умеет самостоятельно принимать решения на основе проведенных исследований.
Оценка "хорошо" выставляется студенту, если он твердо знает материал, грамотно и по существу излагает его, не допуская существенных неточностей в ответе на вопрос, правильно применяет теоретические положения при решении практических вопросов и задач, владеет необходимыми навыками и приемами их выполнения, умеет собирать, систематизировать, анализировать и использовать практический материал для иллюстраций теоретических положений, имеет навыки самостоятельного решения задач на основе изученных методов, приемов, технологий; умеет создавать и применять документы, связанные с профессиональной деятельностью; умеет анализировать современное состояние отрасли.
Оценка "удовлетворительно" выставляется студенту, если он имеет знания только основного материала, но не усвоил его деталей, допускает неточности, недостаточно правильные формулировки, нарушения логической последовательности в изложении программного материала, испытывает затруднения при выполнении практических работ, имеет навыки сбора и использования практического материала для иллюстрации теоретических положений с помощью преподавателя, решает проблему/задачу на основе изученных методов, приемов, технологий с помощью преподавателя; владеет навыками создания и применения документов, связанные с профессиональной деятельностью с помощью преподавателя.
Оценка "неудовлетворительно" выставляется студенту, который не знает значительной части программного материала, допускает существенные ошибки, неуверенно, с большими затруднениями выполняет практические работы, не умеет собирать и использовать практический материал для иллюстраций теоретических положений, не умеет решать проблему/задачу на основе изученных методов, приемов, технологий, испытывает большие затруднения при использовании нормативной документации.
2. Комплект оценочных средств по междисциплинарному курсу
МДК 01.02 Математический аппарат для построения компьютерных сетей
2.1 Входной контроль
1. Что изучает комбинаторика и перечислите ее основные элементы?
2. Что изучает теория вероятностей и где она применяется?
3. Что такое матрица, какие виды матриц вы знаете?
4. Дайте определение вектор, перечислите их виды.
5. Приведите примеры использования комбинаторики, теории вероятностей, матриц по
Вашей специальности.
2.2 Текущий контроль
Контрольная работа по теме: «Решение задач по теории вероятностей и типовым распределениям случайной величины»
|
Вариант № 1 |
|
1. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,4, для второго 0,6, для третьего 0,7. Случайная величина Х - число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения, функцию распределения, 𝑴(𝑿), 𝑫(𝑿), 𝝈(𝒙). |
|
2. Вероятность того, что транзистор имеет скрытые дефекты, равна 0,25. На склад поступило 30 транзисторов. Какое событие вероятнее: что в этой партии имеется 4 транзистора со скрытыми дефектами или 5? |
|
3. Материнская плата состоит из 3000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента равна 0,015. Найти вероятность того, что за время Т откажут, а) 7 элементов; а) не более 10 элементов. |
|
4. Вероятность рождения мальчика равна 0,52. Найти вероятность того, что среди 100 новорожденных окажется ровно: а) 40 мальчиков, б) 50 мальчиков, в) 30 девочек. |
|
5. Игральную кость бросают 500 раз. Какова вероятность того, что число очков, кратное 2, выпадает не менее 180 и не более 200 раз? |
|
Вариант № 2 |
|
1. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,3, для второго 0,4, для третьего 0,9. Случайная величина Х - число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения, функцию распределения, 𝑴(𝑿), 𝑫(𝑿), 𝝈(𝒙). |
|
2. Вероятность того, что двигатель имеет скрытые дефекты, равна 0,1. На склад поступило 40 двигателей. Какое событие вероятнее: что в этой партии имеется 5 двигателей со скрытыми дефектами или 6? |
|
3.Устройство состоит из 800 элементов, работающих независимо один от другого. Вероятность отказа любого элемента равна 0,003. Найти вероятность того, что за время Т откажут, а) 10 элементов; а) не более 7 элементов. |
|
4. Вероятность рождения девочки равна 0,4. Найти вероятность того, что среди 150 новорожденных окажется ровно: а) 30 мальчиков, б) 100 мальчиков, в) 50 девочек. |
|
5.Игральную кость бросают 5000 раз. Какова вероятность того, что число очков, кратное 3, выпадает не менее 480 и не более 500 раз? |
|
Вариант № 3 |
|
1. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,35, для второго 0,8, для третьего 0,5. Случайная величина Х - число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения, функцию распределения, 𝑴(𝑿),𝑫(𝑿), 𝝈(𝒙). |
|
2. Вероятность того, что сетевой фильтр имеет скрытые дефекты, равна 0,15. На склад поступило 100 фильтров. Какое событие вероятнее: что в этой партии имеется 8 фильтров со скрытыми дефектами или 10? |
|
3.Видеоадаптер состоит из 3000 транзисторов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,005. Найти вероятность того, что за время Т откажут, а) ровно 20 элементов; а) не более 5 элементов. |
|
4. Вероятность рождения мальчика равна 0,66. Найти вероятность того, что среди 200 новорожденных окажется ровно: а) 100 мальчиков, б) 80 мальчиков, в) 100 девочек. |
|
5. Игральную кость бросают 1500 раз. Какова вероятность того, что число очков, нечетное, выпадает не менее 400 и не более 465 раз? |
|
Вариант № 4 |
|
1. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,9, для второго 0,4, для третьего 0,4. Случайная величина Х - число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения, функцию распределения, 𝑴(𝑿), 𝑫(𝑿), 𝝈(𝒙). |
|
2. Вероятность того, что роутер имеет скрытые дефекты, равна 0,1. На склад поступило 90 роутеров. Какое событие вероятнее: что в этой партии имеется 4 роутер со скрытыми дефектами или 5? |
|
3.Центральный процессор состоит из 5000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,006. Найти вероятность того, что за время Т откажут, а) ровно 20 элементов; а) не более 6 элементов. |
|
4. Вероятность рождения девочки равна 0,41. Найти вероятность того, что среди 200 новорожденных окажется ровно: а) 45 мальчиков, б) 10 мальчиков, в) 100 девочек. |
|
5. Игральную кость бросают 6000 раз. Какова вероятность того, что число очков, кратное 3, выпадает не менее 1500 и не более 2000 раз? |
|
Вариант № 5 |
|
1. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,5, для второго 0,5, для третьего 0,9. Случайная величина Х - число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения, функцию распределения, 𝑴(𝑿), 𝑫(𝑿), 𝝈(𝒙). |
|
2. Вероятность того, что плеер имеет скрытые дефекты, равна 0,25. На склад поступило 150 плееров. Какое событие вероятнее: что в этой партии имеется 7 плееров со скрытыми дефектами или 10? |
|
3.Смартфон состоит из 8000 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,025. Найти вероятность того, что за время Т откажут, а) ровно 100 элементов; а) не более 5 элементов. |
|
4. Вероятность рождения мальчика равна 0,7. Найти вероятность того, что среди 300 новорожденных окажется ровно: а) 150 мальчиков, б) 50 мальчиков, в) 200 девочек. |
|
5. Игральную кость бросают 4000 раз. Какова вероятность того, что число очков, простое, выпадает не менее 1600 и не более 2100 раз? |
|
Вариант № 6 |
|
1. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,8, для второго 0,8, для третьего 0,5. Случайная величина Х - число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения, функцию распределения, 𝑴(𝑿), 𝑫(𝑿), 𝝈(𝒙). |
|
2. Вероятность того, что МФУ имеет скрытые дефекты, равна 0,3. На склад поступило 60 МФУ. Какое событие вероятнее: что в этой партии имеется 4 МФУ со скрытыми дефектами или 5? |
|
3. Робот состоит из 5500 элементов, работающих независимо один от другого. Вероятность отказа любого элемента в течении времени Т равна 0,007. Найти вероятность того, что за время Т откажут, а) ровно 100 элементов; а) не более 5 элементов. |
|
4. Вероятность рождения девочки равна 0,62. Найти вероятность того, что среди 150 новорожденных окажется ровно: а) 65 мальчиков, б) 20 мальчиков, в) 130 девочек. |
|
5. Игральную кость бросают 3500 раз. Какова вероятность того, что число очков 5 или 1, выпадает не менее 2000 и не более 2100 раз? |
Критерий оценивания «Решение задач по теории вероятностей и типовым распределениям случайной величины». Каждое задание оценивается в 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 5-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 5-балльной системе оценивания учебных достижений студентов |
|
0-1 |
2 ("неудовлетворительно") |
|
2-3 |
3 ("удовлетворительно") |
|
4 |
4 ("хорошо") |
|
5 |
5 ("отлично") |
Контрольная работа по теме: «Решение задач на изображение графов»
1.
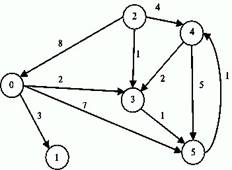 Сколько вершин и ребер имеет граф?
Сколько вершин и ребер имеет граф?
2. Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1.
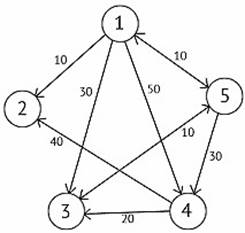 Сколько вершин и ребер имеет граф?
Сколько вершин и ребер имеет граф?
2. Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1. Сколько вершин и ребер имеет граф?
2.
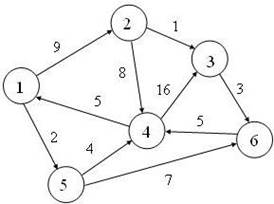 Какие степени вершин в графе?
Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1. Сколько вершин и ребер имеет граф?
2.
 Какие степени вершин в графе?
Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1. Сколько вершин и ребер имеет граф?
2.
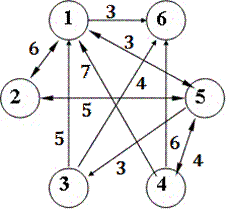 Какие степени вершин в графе?
Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1. Сколько вершин и ребер имеет граф?
2.
 Какие степени вершин в графе?
Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1.
 Сколько вершин и ребер имеет граф?
Сколько вершин и ребер имеет граф?
2. Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1.
 Сколько вершин и ребер имеет граф?
Сколько вершин и ребер имеет граф?
2. Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1.
 Сколько вершин и ребер имеет граф?
Сколько вершин и ребер имеет граф?
2. Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
1. Сколько вершин и ребер имеет граф?
2.
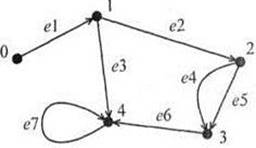 Какие степени вершин в графе?
Какие степени вершин в графе?
3. Полный ли граф?
4. Проверить для графа, что число нечетных вершин любого графа четно.
5. Проверить для графа, что сумма степеней вершин графа число четное, равное удвоенному числу ребер графа?
6. Можно ли начертить граф «одним росчерком»?
7. Сколько циклов в графе?
8. Связанный или не связанный граф?
9. Проверить, что граф с N вершинами имеет N-1 ребро.
10. Найдите степень входа и выхода вершин графа.
11. Составить матрицу смежности графа.
12. Составить матрицу инцидентности графа.
13. Составить список дуг графа.
14. Составить список смежности графа.
15. Какой из способов хранения Вашего графа оптимален с точки зрения объема занимаемой памяти?
Критерий оценивания «Решение задач на изображение графов». Каждое задание оценивается в 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 5-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 5-балльной системе оценивания учебных достижений студентов |
|
0-4 |
2 ("неудовлетворительно") |
|
5-8 |
3 ("удовлетворительно") |
|
9-12 |
4 ("хорошо") |
|
13-15 |
5 ("отлично") |
Контрольная работа по теме: «Решение задач на представление графа в матрице и списке»
Задание: Для графа, заданного матрицей смежности
1. Найти матрицу инцидентности;
2. Построить граф;
3. Составить список дуг, проверить на наличие циклов, найти степень входа и выхода вершин графа.
Вариант 1
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
|
|
1 |
1 |
1 |
|
1 |
1 2 3 4 5 6 |
|
1 |
|
1 |
|
1 |
1 2 3 4 5 6 |
|
1 |
1 |
|
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
|
|
1 |
1 |
1 |
|
||
|
1 |
1 |
|
1 |
1 |
1 |
|
|
|
1 |
|
1 |
|
|
|
|
1 |
1 |
||
|
1 |
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
||
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1
2
3
4
5
6
Вариант 2
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
|
|
1 |
1 |
|
|
1 |
1 2 3 4 5 6 |
|
1 |
|
1 |
1 |
|
1 2 3 4 5 6 |
|
1 |
1 |
|
1 |
|
|
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
1 |
|
1 |
1 |
1 |
|
||
|
|
|
|
1 |
|
1 |
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
1 |
1 |
||
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
|
1 |
|
|
1 |
1 |
||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
1 |
1 |
|
1
2
3
4
5
6
Вариант 3
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
|
|
1 |
|
1 |
|
1 |
1 2 3 |
|
1 |
1 |
1 |
1 |
|
1 2 3 |
|
1 |
|
1 |
1 |
|
|
|
|
1 |
1 |
1 |
1 |
|
|
|
|
1 |
|
1 |
|
1 |
|
1 |
1 |
||
|
|
|
|
1 |
1 |
1 |
|
|
|
1 |
1 |
1 |
|
1 |
|
1 |
|
|
1
2
3
|
|
|
|
|
|
1 |
4 5 6 |
|
|
|
|
1 |
1 |
4 5 6 |
1 |
|
1 |
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
1 |
|
|
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
|
4
5
6
Вариант 4
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
|
|
1 |
|
1 |
1 |
|
1 2 3 4 5 6 |
|
1 |
|
1 |
1 |
1 |
1 2 3 4 5 6 |
|
1 |
1 |
1 |
|
1 |
|
|
|
1 |
|
|
1 |
|
|
1 |
1 |
|
|
1 |
|
1 |
|
|
|
||
|
|
|
|
1 |
1 |
|
|
|
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
1 |
||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
1 |
1 |
|
1 |
|
1 |
1 |
||
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
1 |
|
1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
1 |
1 |
|
1
2
3
4
5
6
Вариант 5
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
|
|
1 |
1 |
|
1 |
1 |
1 2 3 4 5 6 |
|
1 |
1 |
1 |
|
|
1 2 3 4 5 6 |
|
1 |
|
1 |
1 |
1 |
|
|
|
1 |
1 |
|
1 |
|
|
1 |
1 |
|
1 |
1 |
|
1 |
1 |
1 |
|
||
|
|
|
|
1 |
1 |
|
|
|
|
1 |
1 |
1 |
|
1 |
|
1 |
1 |
1 |
||
|
|
|
|
|
|
1 |
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
1 |
|
||
|
|
|
|
|
|
1 |
|
|
|
|
|
1 |
1 |
1 |
1 |
1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
1
2
3
4
5
6
Критерий оценивания «Решение задач на представление графа в матрице и списке». Каждое задание оценивается в 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 5-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 5-балльной системе оценивания учебных достижений студентов |
|
0 |
2 ("неудовлетворительно") |
|
1 |
3 ("удовлетворительно") |
|
2 |
4 ("хорошо") |
|
3 |
5 ("отлично") |
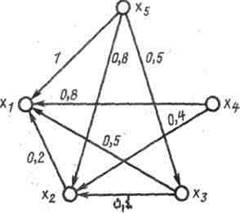
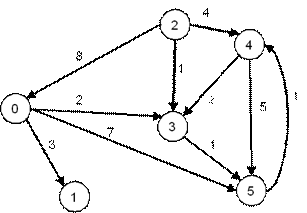
Контрольная работа по теме: «Решение задач на алгоритмы поиска кротчайшего пути и
Краскала»
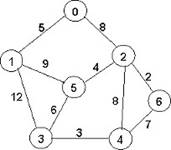
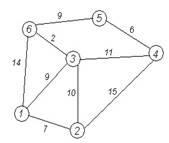
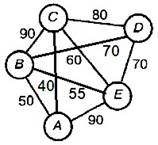
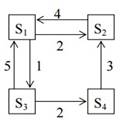
Задание: Найти кратчайшие расстояния от 1-й вершины до всех остальных для графа, представленного на рисунке и найти минимальное отставное дерево (использование алгоритма Краскала).
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
|
|
|
|
|
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
|
|
|
Краскала». Контрольная работа представляет собой два задания. Если задание решено на 100% - 2 балла, если менее 50% - 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 5-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 5-балльной системе оценивания учебных достижений студентов |
|
1 |
2 ("неудовлетворительно") |
|
2 |
3 ("удовлетворительно") |
|
3 |
4 ("хорошо") |
|
4 |
5 ("отлично") |
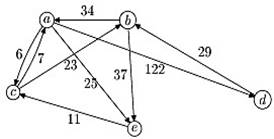
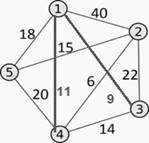
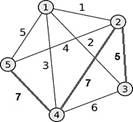
Контрольная работа по теме: «Решение задачи коммивояжера»
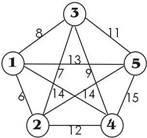
Задание: Для взвешенного неориентированного графа решить задачу коммивояжера (подробный ход решения).
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
|
|
|
|
|
Вариант 4 |
Вариант 5 |
Вариант 6 |
|
|
|
|
Критерий оценивания «Решение задачи коммивояжера». Контрольная работа представляет собой одно задание. Если задание решено на 100% и с пояснением каждого шага – 5 баллов, если задача решена более чем на 70% с пояснением каждого шага - 4 балла, если решена на 50% - 70% с пояснением каждого шага – 3 балла, если менее 50% - 2 балла. Система начисления баллов за правильно выполненное задание для оценивания работ по 5-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 5-балльной системе оценивания учебных достижений студентов |
|
2 |
2 ("неудовлетворительно") |
|
3 |
3 ("удовлетворительно") |
|
4 |
4 ("хорошо") |
|
5 |
5 ("отлично") |
Контрольная работа по теме: «Решение задач на применение теории графов»
Вариант № 1
1.
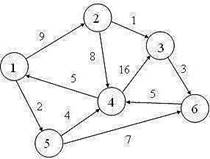 Составить матрицу смежности и инцидентности, список дуг и
смежности для данного графа. Какие степени вершин графа?
Составить матрицу смежности и инцидентности, список дуг и
смежности для данного графа. Какие степени вершин графа?
2. Найдите минимальное остовное дерево с помощью алгоритма Крускала.
3. Найдите кратчайшие пути от одной вершины графа до всех
других с помощью алгоритма Дейкстры.
4. Решите задачу коммивояжера для графа.
 Вариант № 2
Вариант № 2 1. Составить матрицу смежности и инцидентности, список дуг и смежности для данного графа. Какие степени вершин графа?
2. Найдите минимальное остовное дерево с помощью алгоритма Крускала.
3. Найдите кратчайшие пути от одной вершины графа до всех других с помощью алгоритма Дейкстры.
4. Решите задачу коммивояжера для графа.
1.
 Составить матрицу смежности и инцидентности, список дуг и
смежности для данного графа. Какие степени вершин графа?
Составить матрицу смежности и инцидентности, список дуг и
смежности для данного графа. Какие степени вершин графа?
2. Найдите минимальное остовное дерево с помощью алгоритма Крускала.
3. Найдите кратчайшие пути от одной вершины графа до всех других с помощью алгоритма Дейкстры.
4. Решите задачу коммивояжера для графа.
1.
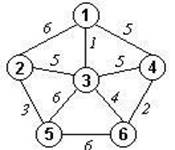 Составить матрицу смежности и инцидентности, список дуг и
смежности для данного графа. Какие степени вершин графа?
Составить матрицу смежности и инцидентности, список дуг и
смежности для данного графа. Какие степени вершин графа?
2. Найдите минимальное остовное дерево с помощью алгоритма Крускала.
3. Найдите кратчайшие пути от одной вершины графа до всех других с помощью алгоритма Дейкстры.
4. Решите задачу коммивояжера для графа.
 Вариант № 5
Вариант № 5 1. Составить матрицу смежности и инцидентности, список дуг и смежности для данного графа. Какие степени вершин графа?
2. Найдите минимальное остовное дерево с помощью алгоритма Крускала.
3. Найдите кратчайшие пути от одной вершины графа до всех других с помощью алгоритма Дейкстры.
4. Решите задачу коммивояжера для графа.
 Вариант
№ 6
Вариант
№ 6
1. Составить матрицу смежности и инцидентности, список дуг и смежности для данного графа. Какие степени вершин графа?
2. Найдите минимальное остовное дерево с помощью алгоритма Крускала.
3. Найдите кратчайшие пути от одной вершины графа до всех других с помощью алгоритма Дейкстры.
4. Решите задачу коммивояжера для графа.
 Вариант
№ 7
Вариант
№ 7
1. Составить матрицу смежности и инцидентности, список дуг и смежности для данного графа. Какие степени вершин графа?
2. Найдите минимальное остовное дерево с помощью алгоритма Крускала.
3. Найдите кратчайшие пути от одной вершины графа до всех других с помощью алгоритма Дейкстры.
4. Решите задачу коммивояжера для графа.
Вариант № 8
1.
 Составить матрицу смежности и инцидентности, список дуг и
смежности для данного графа. Какие степени вершин графа?
Составить матрицу смежности и инцидентности, список дуг и
смежности для данного графа. Какие степени вершин графа?
2. Найдите минимальное остовное дерево с помощью алгоритма Крускала.
3. Найдите кратчайшие пути от одной вершины графа до всех других с помощью алгоритма Дейкстры.
4. Решите задачу коммивояжера для графа.
Критерий оценивания «Решение задач на применение теории графов». Каждое задание оценивается в 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 5-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 5-балльной системе оценивания учебных достижений студентов |
|
1 |
2 ("неудовлетворительно") |
|
2 |
3 ("удовлетворительно") |
|
3 |
4 ("хорошо") |
|
4 |
5 ("отлично") |
Тест по теме: «Понятие и свойства системы, основные понятия теории массового обслуживания»
1. Теория массового обслуживания занимается изучением:
а) систем с элементами случайности, массовостью и процессом обслуживания;
б) систем с элементами предсказуемости и процессом обслуживания;
в) систем элементами постоянства и процессом обслуживания;
2. Что относиться к искусственным системам?
а) клетка, кристалл, экосистема; б) живой организм, телефон, бактерия;
в) машина, искусственный интеллект, органические соединения;
г) здания, машины, компьютеры;
3. Что относиться к естественным системам?
а) клетка, кристалл, экосистема; б) живой организм, телефон, бактерия;
в) машина, искусственный интеллект, органические соединения;
г) здания, машины, компьютеры;
4. Большая система состоит из:
а) разнотипных элементов с разнотипными связями;
б) большого числа однотипных элементов с однотипными связями;
в) разнотипных элементов с однотипными связями;
г) большого числа однотипных элементов с разнотипными связями;
5. Сложная система состоит из:
а) разнотипных элементов с разнотипными связями;
б) большого числа однотипных элементов с однотипными связями;
в) разнотипных элементов с однотипными связями;
г) большого числа однотипных элементов с разнотипными связями;
6. Перечислите задачи исследования систем…
а) анализ и оценка; б) понимание и синтез; в) анализ и синтез; г) знание и понимание;
7. Что подразумевается под инвариантностью системы:
а) минимальная зависимость компонентов состояния или выходов системы от различных возмущений на входных полюсах или изменении параметров системы;
б) семейство реакций состояния и выходов системы на изменение ее параметров, начального состояния, на возмущение и управляющие воздействия;
в) свойство системы, заключающееся в наличии связей между системой и внешней средой;
г) свойство системы сохранять состояние равновесия или некоторого движения при воздействии на нее факторов, вызывающих определенные начальные отклонения;
8. Что подразумевается под устойчивостью системы:
а) минимальная зависимость компонентов состояния или выходов системы от различных возмущений на входных полюсах или изменении параметров системы;
б) семейство реакций состояния и выходов системы на изменение ее параметров, начального состояния, на возмущение и управляющие воздействия;
в) свойство системы, заключающееся в наличии связей между системой и внешней средой;
г) свойство системы сохранять состояние равновесия или некоторого движения при воздействии на нее факторов, вызывающих определенные начальные отклонения;
9. Что подразумевается под управляемостью системы:
а) принципиальная возможность перевода системы из одних состояний в другие с помощью управляющего воздействия, которое выбирается из класса допустимых управлений;
б) семейство реакций состояния и выходов системы на изменение ее параметров, начального состояния, на возмущение и управляющие воздействия;
в) предельно достижимое значение того или иного показателя качества системы для заданных исходных и ограничивающих данных о ней, а также при соответствии этому показателю решения задачи оптимального выбора
г) минимальная зависимость компонентов состояния или выходов системы от различных возмущений на входных полюсах или изменении параметров системы;
10. Что такое заявка?
а) обслуживаемый объект в теории СМО; б) выпускаемый объект из СМО;
в) объект, находящийся в СМО; г) случайный поток;
11. Случайный поток – это
а) поток, создаваемый внутри СМО; б) случайные требования, выходящие в СМО;
в) случайные требования, поступающие в СМО; г) требования, обсуживающиеся в СМО;
12. Цель клиента:
а) обработка заявки за оптимальную цену;
б) заявки и требования - затратить как можно меньше времени, простаивая в очереди;
в) заявки и требования – качество обработанной заявки;
г) оптимальная цена и качество; 13. Цель обслуживающей системы:
а) затрата минимальных ресурсов для обработки заявки;
б) оптимальность инвариантности СМО;
в) обеспечение чувствительности и коммуникативности СМО;
г) как можно меньше времени находиться в состоянии вынужденных простоев;
14. Канал обслуживания -
а) входящий поток данных;
б) средства, обслуживающие требования;
в) выходящий поток требований;
г) канал, пропускаемый заявку в СМО;
15. Выходной поток требований -
а) обработанная заявка клиента;
б) заявка, поступающая в следующую подсистему СМО;
в) обрабатывающаяся заявка в СМО;
г) случайный поток.
Критерий оценивания «Понятие и свойства системы, основные понятия теории массового обслуживания». В тестах 20 вопросов. Каждый вопрос оценивается в 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 4балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 4-балльной системе оценивания учебных достижений студентов |
|
< 8 |
2 ("неудовлетворительно") |
|
8-10 |
3 ("удовлетворительно") |
|
11-13 |
4 ("хорошо") |
|
14-15 |
5 ("отлично") |
|
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
От. |
а |
г |
а |
б |
а |
в |
а |
г |
а |
а |
в |
б |
г |
б |
а |
Ключи:
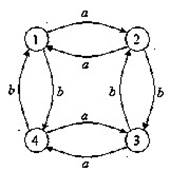
Контрольная работа по теме: «Решение задач на нахождение потоков и предельные
вероятности состояния»
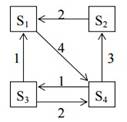 Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное
распределение вероятностей состояния. Составить систему дифференциальных
уравнений Колмогорова для вероятностей состояний.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное
распределение вероятностей состояния. Составить систему дифференциальных
уравнений Колмогорова для вероятностей состояний.
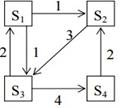 Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное
распределение вероятностей состояния. Составить систему дифференциальных
уравнений Колмогорова для вероятностей состояний.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное
распределение вероятностей состояния. Составить систему дифференциальных
уравнений Колмогорова для вероятностей состояний.
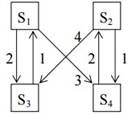 Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
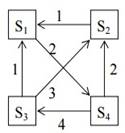 Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный граф
состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный граф
состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
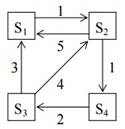 Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение вероятностей
состояния. Составить систему дифференциальных уравнений Колмогорова для
вероятностей состояний.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение вероятностей
состояния. Составить систему дифференциальных уравнений Колмогорова для
вероятностей состояний.
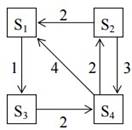 Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
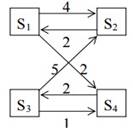 Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
 Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить
матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния. Составить систему дифференциальных уравнений
Колмогорова для вероятностей состояний.
Критерий оценивания «Решение задач на нахождение потоков и предельные вероятности состояния». Задача оценивается в 3 балла и состоит из 3 заданий. Каждое задание оценивается в 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 3-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 3-балльной системе оценивания учебных достижений студентов |
|
0 |
2 ("неудовлетворительно") |
|
1 |
3 ("удовлетворительно") |
|
2 |
4 ("хорошо") |
|
3 |
5 ("отлично") |
Контрольная работа по теме: «Решение задач на процессы гибели и размножения»
Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 2, 𝜆12 = 4, 𝜆23 = 5, 𝜆10 = 4, 𝜆21 = 6, 𝜆23 = 2.
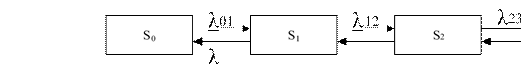 10 λ21 λ32
10 λ21 λ32
Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 1, 𝜆12 = 4, 𝜆23 = 2, 𝜆10 = 3, 𝜆21 = 2, 𝜆23 = 3.
 10 λ21 λ32
10 λ21 λ32
Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 4, 𝜆12 = 2, 𝜆23 = 1, 𝜆10 = 3, 𝜆21 = 1, 𝜆23 = 2.
 10 λ21 λ32
10 λ21 λ32
Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 6, 𝜆12 = 3, 𝜆23 = 2, 𝜆10 = 2, 𝜆21 = 5, 𝜆23 = 1.
 10 λ21 λ32
10 λ21 λ32
Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 2, 𝜆12 = 3, 𝜆23 = 2, 𝜆10 = 1, 𝜆21 = 4, 𝜆23 = 5.
 10 λ21 λ32
10 λ21 λ32
Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 5, 𝜆12 = 1, 𝜆23 = 3, 𝜆10 = 2, 𝜆21 = 1, 𝜆23 = 3.
 10 λ21 λ32
10 λ21 λ32
Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 7, 𝜆12 = 3, 𝜆23 = 1, 𝜆10 = 3, 𝜆21 = 5, 𝜆23 = 1.
 10 λ21 λ32
10 λ21 λ32
Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 3, 𝜆12 = 6, 𝜆23 = 1, 𝜆10 = 2, 𝜆21 = 3, 𝜆23 = 5.
 10 λ21 λ32
10 λ21 λ32
Критерий оценивания «Решение задач на процессы гибели и размножения». Задача оценивается в 3 балла. Если студент правильно написал систему уравнений – 1 балл, нашел предельные вероятности из системы – 1 балл, сделал проверку вероятностей – 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 3-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 3-балльной системе оценивания учебных достижений студентов |
|
0 |
2 ("неудовлетворительно") |
|
1 |
3 ("удовлетворительно") |
|
2 |
4 ("хорошо") |
|
3 |
5 ("отлично") |
Контрольная работа по теме: «Решение задач на одноканальные и многоканальные СМО с отказом»
1. На телефонную линию поступает простейший поток вызовов с интенсивностью 0,9 вызовов в минуту. Производительность телефонной линии 0,7 вызовов в минуту. Определите основные показатели эффективности данной линии.
2. Около магазина имеется парковка для 7 машин. Автомашины подъезжают к магазину с интенсивностью 40 машин в час. Продолжительность нахождения на автостоянке составляет в среднем 20 мин. Стоянка на проезжей части улицы не допускается. Определить характеристики работы парковки.
1. Справочное бюро имеет одну телефонную линию, на которую приходится в среднем 0,4 вызова в минуту. Среднее время разговора 1,3 мин. Определите основные показатели эффективности данного бюро.
2. Дайте оценку работы предприятия, если у нее имеется 6 каналов связи, за один час поступает в среднем 200 телефонных звонков, среднее время ответа на звонок - 0,8 мин.
1. Сборочный участок работает с интенсивность потока 1,5 блоков в минуту. На этом участке работает контролер, который выборочно проверяет изготовленные блоки аппаратуры, средняя продолжительность контрольных операций равна 1,25 минут. Если в момент прибытия очередного блока контролер занят, то этот блок сразу же передается на дальнейшие операции без промежуточного контроля. Производство непрерывное и продолжается до обнаружения дефекта в одном из блоков, в этом случае технологический процесс останавливается, и выясняются причины неисправности. Определите основные показатели эффективности сборочного участка.
2. Дайте оценку работы телефонной компании, если она располагает четырьмя каналами связи, за один час поступает в среднем 120 телефонных звонков, а среднее время ответа на звонок составляет 1,2 мин.
1. В мастерской по ремонту компьютеров в понедельник работает только один мастер, который выполняет заказ в среднем за 25 мин. Клиенты заходят в мастерскую в среднем каждые 35 мин и в случае занятости мастера уходят. Определите основные показатели эффективности мастерской.
2. В типографию с тремя множительными аппаратами поступают заказы от соседних предприятий на размножение рабочей документации. Если все аппараты заняты, то вновь поступающий заказ не принимается. Среднее время работы с одним заказом составляет 2 часа. Интенсивность потока - 0,5 заявки в час. Определите основные показатели эффективности типографии.
1. В результате наблюдений установлено, что интенсивность телефонных звонков диспетчеру скорой помощи, имеющих характер простейших пуассоновских потоков, составляет 1,1 вызовов в минуту, средняя продолжительность разговора (обслуживание клиента) составляет 2,3 мин. Определите основные показатели эффективности диспетчера скорой помощи.
2. В мастерской по техники работают четыре мастера, каждый из которых выполняет заказ в среднем за 20 мин. Клиенты заходят в мастерскую в среднем каждые 25 мин и, если мастера заняты, то уходят. Определите основные показатели эффективности мастерской.
Критерий оценивания «Решение задач на одноканальные и многоканальные СМО с отказом». Контрольная состоит из 2 заданий. Первая задача оценивается в 1 балл, вторая – 2 балла. Система начисления баллов за правильно выполненное задание для оценивания работ по 3-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 3-балльной системе оценивания учебных достижений студентов |
|
0 |
2 ("неудовлетворительно") |
|
1 |
3 ("удовлетворительно") |
|
2 |
4 ("хорошо") |
|
3 |
5 ("отлично") |
Контрольная работа по теме: «Решение задач на одноканальные и многоканальные СМО с ограниченной длиной очереди»
1. Порт имеет один грузовой причал для разгрузки судов. Интенсивность потока составляет 0,5 заходов в сутки. Среднее время разгрузки одного судна 2 суток. Если в очереди на разгрузку стоят 3 судна, то приходящее судно направляется для разгрузки на другой причал. Найти показатели эффективности работы причала.
2. На автозаправочной станции установлены 3 колонки и площадка на 3 автомобиля для ожидания заправки. В среднем на станцию прибывает одна машина каждые 4 минуты. Среднее время обслуживания одной машины - 2,8 мин. Определить характеристики работы автозаправочной станции.
1. На станцию технического осмотра автомобилей, имеющего 3 смотровых поста, в среднем поступает 1 автомобиль за 0,4 часа. Стоянка во дворе вмещает 3 машины. Среднее время работы одного поста - 0,5 часа. Определить характеристики работы СТО.
2. В справочную железнодорожного вокзала поступают телефонные запросы с интенсивностью 80 заявок в час. Оператор справочной отвечает на поступивший звонок в среднем 0,7 мин. Если оператор занят, клиенту выдается сообщение "Ждите ответа", запрос становится в очередь, длина которой не превышает 4 запросов. Дайте оценку работы справочной. Вариант №3
1. В магазин осуществляется завоз товаров автомобилями. В течение дня прибывают в среднем 6 машин. Подсобные помещения для подготовки товаров к продаже позволяют обрабатывать и хранить товар, привезенный двумя машинами. В магазине работают посменно три фасовщика товаров, каждый из которых в среднем может обрабатывать товар одной машины в течение 5 часов. Продолжительность рабочего дня фасовщиков составляет 12 часов. Определить характеристики работы магазина.
2. Авто заправочная станция имеет одну бензоколонку. Предполагается что простейший поток автомашин поступает на станцию с интенсивностью 11 автомашин/ч. Время обслуживания заявки случайная величина которая подчиняется экспоненциальному закону с параметром 14 автомашин/ч. Определить среднее число автомашин на станции. Вариант №4
1. На строительную площадку в среднем через 40 мин прибывают автомашины со строительным материалом. Среднее время разгрузки одной автомашины составляет 1,8 часа. В разгрузке принимают участие две бригады грузчиков. На территории строительной площадки может находиться в очереди на разгрузку не более 5 автомашин. Определить показатели эффективности работы строительной площадки.
2. Имеется пункт проведения профилактического осмотра машин с одной группой проведения осмотра. На осмотр и выявление дефектов каждой машины затрачивается в среднем 0,4 часа. На осмотр поступает в среднем 328 машин в сутки. Потоки заявок и обслуживаний - простейшие. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она покидает пункт осмотра необслуженной. Определить предельные вероятности состояний и характеристики обслуживания пункта профилактического осмотра. Вариант №5
1. Таможня располагает тремя терминалами. Интенсивность потока автомашин, перевозящих грузы и подлежащих прохождению таможенного контроля, составляет 30 шт. в сутки. Среднее время таможенной обработки на терминале одной автомашины составляет 3 часа. Если в очереди на прохождение таможенного контроля стоят 5 автомашин, то приезжающие автомашины уезжают на другую таможню. Найти показатели эффективности работы таможни.
2. Специализированный пост диагностики представляет собой одноканальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно 3. Если все стоянки заняты, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность 0.85 (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем составляет 1.05 час. Требуется определить вероятностные характеристики поста диагностики, работающего в стационарном режиме.
Критерий оценивания «Решение задач на одноканальные и многоканальные СМО с ограниченной длинной очереди». Контрольная состоит из 2 заданий. Первая задача оценивается в 1 балл, вторая – 2 балла. Система начисления баллов за правильно выполненное задание для оценивания работ по 3-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 3-балльной системе оценивания учебных достижений студентов |
|
0 |
2 ("неудовлетворительно") |
|
1 |
3 ("удовлетворительно") |
|
2 |
4 ("хорошо") |
|
3 |
5 ("отлично") |
Контрольная работа по теме: «Решение задач на одноканальные и многоканальные СМО с
неограниченной длиной очереди»
1. Сборочный участок производит в один час в среднем 90 блоков. На этом участке работает контролер, который проверяет все собранные блоки, средняя продолжительность контрольных операций составляет в среднем 1,25 минут. Определите основные показатели участка.
2. В расчетном узле магазина самообслуживания работает три кассы. Интенсивность входящего потока составляет 5 покупателей в минуту. Интенсивность обслуживания каждым контролером-кассиром составляет 2 покупателя в минуту. Определить характеристики СМО и дать оценку ее работы.
1. Железнодорожную станцию обслуживает касса с одним окном. В летние выходные дни интенсивность потока пассажиров к кассе составляет 0.45 человек в минуту. Кассир затрачивает на облуживание пассажира в среднем 2 мин. Определите основные показатели станции.
2. В многоканальную СМО с тремя каналами обслуживания поступают заявки с интенсивностью 0,7 заявок в час. (Поток заявок простейший). Поток обслуживания имеет интенсивность 0,4 заявки в час. Очередь заявок на обслуживание может расти практически неограниченно. Определите все средние характеристики системы. Вариант №3
1. Порт имеет один грузовой причал для разгрузки судов. Интенсивность потока судов составляет 0.5 судов в сутки. Разгрузка судна требует в среднем 1,5 суток. Предполагается, что суда могут ждать в очереди неограниченно долго. Найти показатели эффективности работы причала.
2. В морском порту четыре причала, интенсивность входного потока - 3,5 судов в сутки. Интенсивность погрузочно-разгрузочных работ – 2,5 судна в день. Поток заявок и поток обслуживания пуассоновские. Очередь судов может расти практически неограниченно. Имея в виду стационарный режим работы, определить все средние характеристики системы. Вариант №4
1. К базе данных сервера продажи билетов поступает 10 запросов в секунду. Среднее время обработки каждого запроса составляет 1 секунду. Запрос, поступивший в момент обработки одного из ранее поступивших запросов, становится в очередь. Определите основные показатели сервера.
2. На торговом складе четыре точки обслуживания, интенсивность входного потока - 7,5 машин в сутки. Интенсивность погрузочно-разгрузочных работ – 1,5 судна в день. Поток заявок и поток обслуживания пуассоновские. Очередь судов может расти практически неограниченно.
Имея в виду стационарный режим работы, определить все средние характеристики системы.
1. Система массового обслуживания — билетная касса с одним окошком и неограниченной очередью. Касса продает билеты в пункты А и В. Пассажиров, желающих купить билет в пункт А, приходит в среднем трое за 20 мин, в пункт В — двое за 20 мин. Поток пассажиров простейший. Кассир в среднем обслуживает трех пассажиров за 10 мин. Время обслуживания показательное. Определите основные показатели кассы.
2. В многоканальную СМО с четырьмя каналами обслуживания поступают заявки с интенсивностью 2,5 заявок в час. (Поток заявок простейший). Поток обслуживания имеет интенсивность 1,5 заявки в час. Очередь заявок на обслуживание может расти практически неограниченно. Определите все средние характеристики системы.
Критерий оценивания «Решение задач на одноканальные и многоканальные СМО с неограниченной длинной очереди». Контрольная состоит из 2 заданий. Первая задача оценивается в 1 балл, вторая – 2 балла. Система начисления баллов за правильно выполненное задание для оценивания работ по 3-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 3-балльной системе оценивания учебных достижений студентов |
|
0 |
2 ("неудовлетворительно") |
|
1 |
3 ("удовлетворительно") |
|
2 |
4 ("хорошо") |
|
3 |
5 ("отлично") |
Контрольная работа по теме: «Решение задач по теории массового обслуживания»
1. Рассматривается работа сервисного центра с А компьютерами. Если заняты все компьютера, то заявка не встает в очередь, а покидает сервиз. Среднее время обработки заявки В мин. Интенсивность потока автомобилей - С ед/мин. Найти предельные вероятности состояний и показатели эффективности работы сервиса.
2. Специализированный пост диагностики представляет собой А-канальную СМО. Число стоянок для автомобилей, ожидающих проведения диагностики, ограниченно и равно В. Если все стоянки заняты, то очередной автомобиль, прибывший на диагностику, в очередь на обслуживание не становится. Поток автомобилей, прибывающих на диагностику, распределен по закону Пуассона и имеет интенсивность С (автомобиля в час). Время диагностики автомобиля распределено по показательному закону и в среднем составляет D час(ов). Требуется определить вероятностные характеристики поста диагностики и его показатели эффективности работы.
3. В морском порту А причала, интенсивность входного потока – В судов в сутки. Интенсивность погрузочно-разгрузочных работ - С судна в день. Поток заявок и поток обслуживания пуассоновские. Очередь судов может расти практически неограниченно. Требуется определить вероятностные характеристики и показатели эффективности работы порта.
|
№ варианта |
|
1 задача |
|
|
2 задача |
|
|
3 задача |
|
|
|
𝑨 |
𝑩 |
C |
A |
B |
𝑪 |
𝑫 |
𝑨 |
𝑩 |
C |
|
|
1 |
3 |
1 |
4 |
3 |
6 |
5 |
8 |
3 |
2 |
3 |
|
2 |
5 |
9 |
9 |
4 |
3 |
9 |
11 |
2 |
10 |
5 |
|
3 |
4 |
6 |
8 |
5 |
5 |
2 |
3 |
5 |
3 |
4 |
|
4 |
4 |
4 |
5 |
3 |
4 |
6 |
7 |
3 |
4 |
2 |
|
5 |
3 |
2 |
3 |
4 |
5 |
4 |
2 |
5 |
11 |
4 |
|
6 |
6 |
8 |
10 |
5 |
6 |
8 |
12 |
4 |
13 |
7 |
|
7 |
5 |
5 |
9 |
3 |
5 |
10 |
8 |
6 |
4 |
5 |
|
8 |
3 |
5 |
7 |
4 |
4 |
9 |
6 |
4 |
5 |
6 |
|
9 |
4 |
3 |
12 |
5 |
3 |
3 |
13 |
5 |
12 |
9 |
|
10 |
5 |
8 |
3 |
3 |
5 |
5 |
8 |
2 |
9 |
4 |
|
11 |
3 |
6 |
19 |
4 |
4 |
7 |
7 |
5 |
5 |
2 |
|
12 |
6 |
4 |
5 |
5 |
3 |
4 |
10 |
6 |
7 |
4 |
|
13 |
5 |
4 |
16 |
3 |
6 |
2 |
5 |
3 |
8 |
8 |
|
14 |
4 |
7 |
21 |
4 |
4 |
7 |
4 |
5 |
7 |
2 |
|
15 |
5 |
7 |
8 |
5 |
3 |
8 |
9 |
4 |
6 |
8 |
|
16 |
3 |
10 |
23 |
3 |
6 |
3 |
2 |
4 |
11 |
6 |
|
17 |
4 |
2 |
18 |
4 |
4 |
6 |
5 |
3 |
4 |
5 |
|
18 |
5 |
4 |
14 |
5 |
3 |
2 |
12 |
2 |
8 |
4 |
|
19 |
4 |
1 |
9 |
3 |
5 |
9 |
9 |
5 |
5 |
3 |
|
20 |
3 |
9 |
8 |
4 |
4 |
4 |
11 |
2 |
9 |
4 |
|
21 |
6 |
5 |
12 |
5 |
6 |
7 |
4 |
3 |
7 |
5 |
|
22 |
3 |
8 |
17 |
3 |
3 |
5 |
6 |
4 |
5 |
7 |
|
23 |
4 |
4 |
24 |
4 |
4 |
10 |
3 |
6 |
10 |
6 |
|
24 |
5 |
6 |
19 |
5 |
5 |
3 |
13 |
3 |
4 |
7 |
|
25 |
6 |
2 |
17 |
3 |
3 |
6 |
5 |
4 |
11 |
5 |
|
26 |
4 |
1 |
12 |
4 |
6 |
8 |
10 |
5 |
3 |
8 |
Критерий оценивания «Решение задач по теории массового обслуживания». Контрольная состоит из 3 заданий. Каждая задача оценивается в 1 балл. Система начисления баллов за правильно выполненное задание для оценивания работ по 3-балльной шкале оценивания учебных достижений студентов приведено в таблице 1.
Таблица 1.
|
Количество набранных баллов |
Оценка по 3-балльной системе оценивания учебных достижений студентов |
|
0 |
2 ("неудовлетворительно") |
|
1 |
3 ("удовлетворительно") |
|
2 |
4 ("хорошо") |
|
3 |
5 ("отлично") |
2.3 Практические занятия
Практическое занятие № 1.
Тема: Решение задач на нахождение вероятностей случайных событий.
Цель: Научиться решать типовые задачи на нахождение вероятностей случайных событий с применением комбинаторики.
Практическое занятие № 2.
Тема: Решение задач на нахождение числовых характеристик дискретной случайной величины.
Научиться решать типовые задачи на нахождение числовых характеристик дискретной случайной величины с применением теории вероятностей и комбинаторики.
Практическое занятие № 3.
Тема: Решение задач на типовые распределения случайной величины.
Цель: Научиться решать типовые случайной величины с применением теории вероятностей и комбинаторики.
Практическое занятие № 4.
Тема: Решение задач по теории вероятностей и типовым распределениям случайной величины. Цель: Закрепление знаний по решению задач на нахождение числовых характеристик дискретной случайной величины и типовым распределениям случайной величины с применением теории вероятностей и комбинаторики.
Практическое занятие № 5.
Тема: Решение задач на изображение графов.
Цель: Изучить основы теоретико-множественного и графического представлений графов, простейших свойств графов, получить практический навык задания и визуализации графа на плоскости; изучить алгоритм поиска эйлерова, гамильтонова цикла (пути) в графе, рассмотреть на конкретных примерах ориентированные и неориентированные графы.
Практическое занятие № 6.
Тема: Решение задач на представление графа в матрице и списке.
Цель: Изучение матричных способов представления графов; отработать на примерах основные понятия теории графов; научить строить графы по матрице и списку; по графу составлять матрицу смежности и списки; закрепить навыки моделирования графов.
Практическое занятие № 7.
Тема: Решение задач на алгоритмы поиска кратчайшего пути и Краскала.
Цель: Изучить и отработать навыки в применении алгоритма поиска кратчайшего пути и алгоритма Краскала; закрепить навыки моделирования (построения)графов.
Практическое занятие № 8.
Тема: Решение задач коммивояжера.
Цель: Изучить и отработать навыки в применении алгоритма поиска оптимального кратчайшего пути проходящего через все вершины графа один раз для решения задач коммивояжера.
Практическое занятие № 9.
Тема: Решение задач на применение теории графов.
Научиться решить задачи на применение теории графов, анализа графа и его характеристик.
Практическое занятие № 10.
Тема: Решение задач на применение теории графов.
Цель: Закрепление знаний по решению задач на применение теории графов, анализа графа и его характеристик.
Практическое занятие № 11.
Тема: Решение задач на нахождение потоков и предельные вероятности состояния.
Цель: Научиться решить задачи на нахождение потоков и предельных вероятностей состояний.
Практическое занятие № 12.
Тема: Решение задач на нахождение потоков и предельные вероятности состояния.
Цель: Закрепление знаний по решению задач на нахождение потоков и предельных вероятностей состояний.
Практическое занятие № 13.
Тема: Решение задач на процессы гибели и размножения.
Цель: Научиться решить задачи на процессы гибели и размножения.
Практическое занятие № 14.
Тема: Решение задач на процессы гибели и размножения.
Цель: Закрепление знаний по решению задач на процессы гибели и размножения.
Практическое занятие № 15.
Тема: Решение задач на одноканальные и многоканальные СМО с отказом.
Цель: Научиться решить задачи на одноканальные и многоканальные системы массового обслуживания с отказом
Практическое занятие № 16.
Тема: Решение задач на одноканальные и многоканальные СМО с отказом.
Цель: Закрепление знаний по решению задач на одноканальные и многоканальные системы массового обслуживания с отказом.
Практическое занятие № 17.
Тема: Решение задач на одноканальные и многоканальные СМО с ограниченной длиной очереди.
Решение задач на одноканальные и многоканальные системы массового обслуживания с ограниченной длиной очереди.
Практическое занятие № 18.
Тема: Решение задач на одноканальные и многоканальные СМО с ограниченной длиной очереди.
Цель: Закрепление знаний по решению задач на одноканальные и многоканальные системы массового обслуживания с ограниченной длиной очереди.
Практическое занятие № 19.
Тема: Решение задач на одноканальные и многоканальные СМО с неограниченной очередью. Цель: Решение задач на одноканальные и многоканальные системы массового обслуживания с неограниченной очередью.
Практическое занятие № 20.
Тема: Решение задач на одноканальные и многоканальные СМО с неограниченной очередью. Цель: Закрепление знаний по решению задач на одноканальные и многоканальные системы массового обслуживания с неограниченной длиной очереди.
Практическое занятие № 21.
Тема: Решение задач по теории массового обслуживания.
Цель: Решение задач на одноканальные и многоканальные СМО с отказом, ограниченной и неограниченной длинной очереди, процессы гибели и размножения.
Практическое занятие № 22.
Тема: Решение задач по теории массового обслуживания.
Цель: Закрепление знаний по решению задач на различные виды систем массового обслуживания.
3. Экзаменационные материалы, содержащие комплект утвержденных по установленной форме экзаменационных билетов
Министерство образования, науки и молодежи Республики Крым Государственное бюджетное профессиональное образовательное учреждение Республики Крым
«Феодосийский политехнический техникум»
Цикловая комиссия компьютерных дисциплин
Утверждаю:
Заместитель директора по учебной работе О.Г. Сердюкова
«____» _______ 2016 г.
в рамках программы подготовки специалистов среднего звена
по специальности среднего профессионального образования
09.02.02 Компьютерные сети
Феодосия, 2016
Организация - разработчик: Государственное бюджетное профессиональное образовательное учреждение Республики Крым «Феодосийский политехнический техникум»
Разработчик: преподаватель Г.А. Кузьмич
Комплект экзаменационных билетов по МДК 01.02 Математический аппарат для построения компьютерных сетей рассмотрен и одобрен на заседании цикловой комиссии компьютерных дисциплин Протокол № 9 от «6» апреля 2016 г.
Председатель ЦК ____________ Т.Н. Дворянова
Комплект экзаменационных билетов по
МДК 01.02 Математический аппарат для построения компьютерных сетей рассмотрен и одобрен на заседании методического совета Протокол № 6 от «27» апреля 2016 г.
Председатель методического совета ____________ О.Г. Сердюкова
Старший методист ____________ Т.Н. Старовойтова Экзаменационный билет № 1
1. ![]() Комбинаторика
и ее основные элементы.
Комбинаторика
и ее основные элементы.
2. Безразмерные графы.
3. Найти кратчайшие расстояния от 1-й вершины до всех остальных для графа, представленного на рисунке и найти минимальное отставное дерево (использование алгоритма Краскала).
4. Междугородный переговорный пункт имеет четыре телефонных аппарата. В среднем за сутки поступает 320 заявок на переговоры. Средняя длительность переговоров составляет 5 мин. Длина очереди не должна превышать 6 абонентов. Потоки заявок и обслуживаний простейшие. Определить характеристики обслуживания переговорного пункта в стационарном режиме (вероятность простоя каналов, вероятность отказа, вероятность обслуживания, среднее число занятых каналов, среднее число заявок в очереди, среднее число заявок в системе, абсолютную пропускную способность, относительную пропускную способность, среднее время заявки в очереди, среднее время заявки в системе, среднее время заявки под обслуживанием).
1. Основные понятия теории вероятности.
1 2 3 4 5 6
2. Задача коммивояжера – метод ветвей и границ.
|
|
1 |
1 |
|
|
1 |
|
|
|
1 |
1 |
1 |
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1
3. Для графа, заданного матрицей смежности: найти матрицу 2
3
инцидентности; построить граф; составить список дуг, проверить на
4
наличие циклов, найти степень входа и выхода вершин графа. 5
6
4. Система массового обслуживания — билетная касса с одним окошком и неограниченной очередью. Касса продает билеты в пункты А и В. Пассажиров, желающих купить билет в пункт А, приходит в среднем трое за 20 мин, в пункт В — двое за 20 мин. Поток пассажиров простейший. Кассир в среднем обслуживает трех пассажиров за 10 мин. Время обслуживания — показательное. Вычислить финальные вероятности Р1, P2, P3, среднее число заявок в системе и в очереди, среднее время пребывания заявки в системе, среднее время пребывания заявки в очереди.
1. Теоремы сложения и умножения вероятностей.
2. Основные проблемы синтеза графов атак.
3. Опишите основные характеристики графа:
4. Интенсивность потока телефонных звонков в агентство по заказу железнодорожных билетов, имеющему один телефон, составляет 16 вызовов в час. Продолжительность оформления заказа на билет равна 2.4 минуты. Определить относительную и абсолютную пропускную способность этой СМО и вероятность отказа (занятости телефона). Сколько телефонов должно быть в агентстве, чтобы относительная пропускная способность была не менее 0,75.
1. Условная вероятность.
1 2 3 4 5 6
|
|
1 |
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
2. Приложения теории графов. 1
2
3. Для графа, заданного матрицей смежности: найти матрицу 3 инцидентности; построить граф; составить список дуг, проверить на 4
наличие циклов, найти степень входа и выхода вершин графа. 5
6
4. В многоканальную СМО с четырьмя каналами обслуживания поступают заявки с интенсивностью 2,5 заявок в час. (Поток заявок простейший). Поток обслуживания имеет интенсивность 1,5 заявки в час. Очередь заявок на обслуживание может расти практически неограниченно. Определите все средние характеристики системы.
1. Формула полной вероятности и формула Байеса.
2. Понятие и свойства системы.
3. Опишите основные характеристики графа:
4. В расчетном узле магазина самообслуживания работает три кассы. Интенсивность входящего потока составляет 5 покупателей в минуту. Интенсивность обслуживания каждым контролером-кассиром составляет 2 покупателя в минуту. Определить характеристики СМО и дать оценку ее работы.
1. Дискретная случайная величина.
2. Основные свойства систем. 1 2 3 4 5 6
|
|
1 |
1 |
1 |
|
1 |
|
1 |
|
1 |
|
|
1 |
|
1 |
1 |
|
1 |
1 |
1 |
|
1 |
|
1 |
|
|
1 |
|
|
|
1 |
|
|
1 |
|
1 |
1 |
1 |
1 |
1 |
|
1 1
3. Для графа, заданного матрицей смежности: найти матрицу 2 2
3 3
инцидентности; построить граф; составить список дуг, проверить
4 4
на наличие циклов, найти степень входа и выхода вершин графа. 5 5
6 6
4. К базе данных сервера продажи билетов поступает 10 запросов в секунду. Среднее время обработки каждого запроса составляет 1 секунду. Запрос, поступивший в момент обработки одного из ранее поступивших запросов, становится в очередь. Определите основные показатели сервера.
1. Числовые характеристики дискретной случайной величины.
2. Основные понятия системы массового обслуживания.
3. Опишите основные характеристики графа:
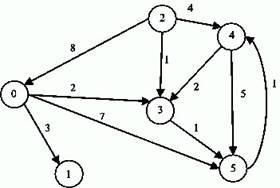
4. Железнодорожную станцию обслуживает касса с одним окном. В летние выходные дни интенсивность потока пассажиров к кассе составляет 0.45 человек в минуту. Кассир затрачивает на облуживание пассажира в среднем 2 мин. Определите основные показатели станции.
1. Моменты распределений.
2. Показатели эффективности СМО.
3. Между девятью планетами Солнечной системы установлено космическое сообщение.
Рейсовые ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера,
Земля — Плутон, Плутон — Меркурий, Меркурий — Венера, Уран — Нептун, Нептун — Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. По каждому маршруту ракеты летают в обе стороны. Можно ли долететь на рейсовых ракетах от Земли до Марса?
4. В многоканальную СМО с тремя каналами обслуживания поступают заявки с интенсивностью 0,7 заявок в час. (Поток заявок простейший). Поток обслуживания имеет интенсивность 0,4 заявки в час. Очередь заявок на обслуживание может расти практически неограниченно. Определите все средние характеристики системы.
1. Равномерное распределение непрерывной случайной величины.
2. Классификация систем массового обслуживания.
3. Составить матрицу смежности и инцидентности, список дуг и смежности для данного графа.
Какие степени вершин графа?
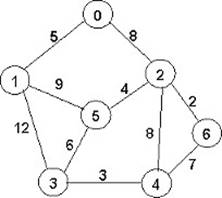
4. В расчетном узле магазина самообслуживания работает три кассы. Интенсивность входящего потока составляет 5 покупателей в минуту. Интенсивность обслуживания каждым контролером-кассиром составляет 2 покупателя в минуту. Определить характеристики СМО и дать оценку ее работы.
1. Нормальный закон распределения непрерывной случайной величины.
2. Случайные процессы. Граф состояний.
3. Составить матрицу смежности и инцидентности, список дуг и смежности для данного графа.
Какие степени вершин графа?
4. Авто заправочная станция имеет одну бензоколонку. Предполагается что простейший поток автомашин поступает на станцию с интенсивностью 11 автомашин/ч. Время обслуживания заявки случайная величина которая подчиняется экспоненциальному закону с параметром 14 автомашин/ч. Определить среднее число автомашин на станции.
1. Показательное распределение непрерывной случайной величины.
2. Марковские процессы.
3. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,5, для второго-0,8, для третьего -0,7. Случайная величина Х- число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения,
𝑀(𝑋), 𝐷(𝑋).
4. В типографию с тремя множительными аппаратами поступают заказы от соседних предприятий на размножение рабочей документации. Если все аппараты заняты, то вновь поступающий заказ не принимается. Среднее время работы с одним заказом составляет 2 часа. Интенсивность потока - 0,5 заявки в час. Определите основные показатели эффективности типографии.
1. Распределение Бернулли, Пуассона.
2. Моделирование Марковского процесса.
3.
![]() Три стрелка стреляют по мишени. Вероятность попадания в
мишень при одном выстреле для первого стрелка равна 0,5, для второго - 0,7 для
третьего - 0,8. Случайная величина Х - число попаданий в мишень, если стрелки
делают по одному выстрелу. Найти закон распределения случайной величины.
Три стрелка стреляют по мишени. Вероятность попадания в
мишень при одном выстреле для первого стрелка равна 0,5, для второго - 0,7 для
третьего - 0,8. Случайная величина Х - число попаданий в мишень, если стрелки
делают по одному выстрелу. Найти закон распределения случайной величины.
4. Для взвешенного неориентированного графа решить задачу коммивояжера (подробный ход решения).
1. Распределение Релея.
2. Потоки событий.
3. Игральную кость бросают 4000 раз. Какова вероятность того, что число очков, простое, выпадает не менее 1800 и не более 2200 раз?
4. ![]() Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния.
1. Основные понятия теории графов.
2. Классификация случайных процессов и их характеристика.
3. Вероятность рождения мальчика равна 0,65. Найти вероятность того, что среди 100 новорожденных окажется ровно 50 мальчиков.
4. Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 1, 𝜆12 = 4, 𝜆23 = 5, 𝜆10 = 2, 𝜆21 = 2, 𝜆23 = 3.
 10 λ21 λ32
10 λ21 λ32
1. Перечислите основные понятия, связанные с неориентированными графами.
2. Предельные вероятности состояний.
3. Устройство состоит из 800 элементов, работающих независимо один от другого. Вероятность отказа любого элемента равна 0,003. Найти вероятность того, что за время Т откажут 10 элементов.
4. ![]() Найти
кратчайшие расстояния от 1-й вершины до всех остальных для графа,
представленного на рисунке и найти минимальное отставное дерево (использование
алгоритма
Найти
кратчайшие расстояния от 1-й вершины до всех остальных для графа,
представленного на рисунке и найти минимальное отставное дерево (использование
алгоритма
Краскала).
1. Маршрут, цикл и цепь графа.
2. Решение матричных игр в смешанных стратегиях.
3. Вероятность того, что транзистор имеет скрытые дефекты, равна 0,25. На склад поступило 30 транзисторов. Какое событие вероятнее: что в этой партии имеется 4 транзистора со скрытыми дефектами или 5?
4. В мастерской по ремонту компьютеров в понедельник работает только один мастер, который выполняет заказ в среднем за 25 мин. Клиенты заходят в мастерскую в среднем каждые 35 мин и в случае занятости мастера уходят. Определите основные показатели эффективности мастерской.
1. Эйлеровы и Гамильтоновы графы.
2. Процессы гибели и размножения.
3. Студенту на контрольной работе предложили 8 конвертов с заданиями. Из них 6 конвертов содержат простые задания, остальные – сложные. Какова вероятность того, что, случайным образом выбирая конверты, студент сначала возьмет конверт с простым, а затем со сложным заданием?
4. На станцию технического осмотра автомобилей, имеющего 3 смотровых поста, в среднем поступает 1 автомобиль за 0,4 часа. Стоянка во дворе вмещает 3 машины. Среднее время работы одного поста - 0,5 часа. Определить характеристики работы СТО.
1. Деревья и их свойства, перечисление деревьев.
2. Элементы теории игр и матричные игры в чистых стратегиях.
3. В урне находится 17 шаров: 9 белых, остальные – черные. Какова вероятность того, что первый, извлеченный из урны шар будет белый, а следующий черный?
4. ![]() Найти
кратчайшие расстояния от 1-й вершины до всех остальных для графа,
представленного на рисунке и найти минимальное отставное
Найти
кратчайшие расстояния от 1-й вершины до всех остальных для графа,
представленного на рисунке и найти минимальное отставное
дерево (использование алгоритма Краскала).
1. Графы деревьев.
2. Одноканальные СМО с отказом.
3. Имеется 4 карточки с буквами В, С, А, Я. Какова вероятность того, что студент, извлекая по одной карточке, сможет сложить из них свое имя? Как зовут студента?
4. ![]() Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния.
1. Представление графа в матрице и списке.
2. Многоканальные СМО с отказом.
3. Решить уравнение: 6𝐶𝑥3 = 11𝐴2𝑥−1.
4. Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 2, 𝜆12 = 3, 𝜆23 = 4, 𝜆10 = 1, 𝜆21 = 2, 𝜆23 = 2.
 10 λ21 λ32
10 λ21 λ32
1. Матрица смежностей и инциденций.
2. Одноканальные СМО с ограниченной длиной очереди.
3. Решить уравнение: 𝐶𝑥2+1 = 36.
4. Сборочный участок работает с интенсивность потока 1,5 блоков в минуту. На этом участке работает контролер, который выборочно проверяет изготовленные блоки аппаратуры, средняя продолжительность контрольных операций равна 1,25 минут. Если в момент прибытия очередного блока контролер занят, то этот блок сразу же передается на дальнейшие операции без промежуточного контроля. Производство непрерывное и продолжается до обнаружения дефекта в одном из блоков, в этом случае технологический процесс останавливается, и выясняются причины неисправности. Определите основные показатели эффективности сборочного участка.
Экзаменационный билет № 22
1. Алгоритм Краскаля.
2. Многоканальные СМО с ограниченной длиной очереди.
![]() 𝐴5𝑥+1−
𝐴3𝑥
𝐴5𝑥+1−
𝐴3𝑥
3. Решить уравнение: 𝐴3𝑥 = 4.
4. Для взвешенного неориентированного графа решить задачу коммивояжера (подробный ход решения).
1. Алгоритмы поиска кратчайшего пути.
2. Многоканальные СМО с неограниченной длиной очереди.
3. В стандартной колоде 36 карт. Из четырех тузов разных мастей извлекается один, запоминается, затем возвращается обратно. Затем извлекается вторая карта. Сколькими способами можно выбрать таким образом пару тузов?
4. Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 3, 𝜆12 = 1, 𝜆23 = 3, 𝜆10 = 2, 𝜆21 = 2, 𝜆23 = 1.
 10 λ21 λ32
10 λ21 λ32
1. Алгоритм Дейкстры.
2. Одноканальные СМО с неограниченной очередью.
3. Студент выучил 17 экзаменационных билетов, а 8 оставшихся не выучил. Какова вероятность, что студент не получит «двойку» (А), что получит «двойку» (B)?
4. ![]() Для
взвешенного неориентированного графа решить задачу коммивояжера
(подробный ход решения).
Для
взвешенного неориентированного графа решить задачу коммивояжера
(подробный ход решения).
1.. Перечислите основные характеристики ориентированного графа.
2. Смешанные стратегии 2 х 2.
3. Доставка груза может быть осуществлена шестью дорогами. Сколькими способами менеджер может составить маршрут для двух машин, если они должны ехать различными путями?
4. Дайте оценку работы предприятия, если у нее имеется 6 каналов связи, за один час поступает в среднем 200 телефонных звонков, среднее время ответа на звонок - 0,8 мин.
1.. Различие между Эйлеровыми и Гамильтоновыми графами.
2. Применение СМО в вашей специальности.
3. На кафедре работает 4 профессора. Они должны прочесть 2 лекции, причем один человек может прочитать обе лекции. Порядок прочтения лекций важен. Сколькими способами можно отобрать кандидатов для прочтения лекций?
4. ![]() Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния.
Рассматривается
система с дискретными состояниями и непрерывным временем. Заданы размеченный
граф состояний и интенсивности переходов. Все потоки событий простейшие.
Составить матрицу интенсивностей переходов. Найти предельное распределение
вероятностей состояния.
Приложение
1. Комбинаторика и ее основные элементы.
2. Основные понятия теории вероятности.
3. Теоремы сложения и умножения вероятностей.
4. Условная вероятность.
5. Формула полной вероятности и формула Байеса.
6. Дискретная случайная величина.
7. Числовые характеристики дискретной случайной величины.
8. Моменты распределений.
9. Равномерное распределение непрерывной случайной величины.
10. Нормальный закон распределения непрерывной случайной величины.
11. Показательное распределение непрерывной случайной величины
12. Распределение Релея.
13. Распределение Бернулли, Пуассона.
14. Основные понятия теории графов.
15. Перечислите основные понятия, связанные с неориентированными графами.
16. Маршрут, цикл и цепь графа.
17. Эйлеровы и Гамильтоновы графы.
18. Деревья и их свойства, перечисление деревьев.
19. Графы деревьев.
20. Представление графа в матрице и списке.
21. Матрица смежностей и инциденций.
22. Безразмерные графы.
23. Алгоритм Краскаля.
24. Алгоритмы поиска кратчайшего пути.
25. Алгоритм Дейкстры.
26. Задача коммивояжера – метод ветвей и границ.
27. Основные проблемы синтеза графов атак.
28. Приложения теории графов.
29. Понятие и свойства системы.
30. Основные свойства систем.
31. Основные понятия системы массового обслуживания.
32. Показатели эффективности СМО.
33. Классификация систем массового обслуживания.
34. Случайные процессы. Граф состояний.
35. Классификация случайных процессов и их характеристика.
36. Марковские процессы.
37. Моделирование Марковского процесса.
38. Потоки событий.
39. Предельные вероятности состояний.
40. Процессы гибели и размножения.
41. Одноканальные СМО с отказом.
42. Многоканальные СМО с отказом.
43. Одноканальные СМО с ограниченной длиной очереди.
44. Многоканальные СМО с ограниченной длиной очереди.
45. Одноканальные СМО с неограниченной очередью.
46. Многоканальные СМО с неограниченной очередью.
47. Элементы теории игр и матричные игры в чистых стратегиях.
48. Решение матричных игр в смешанных стратегиях.
1. Доставка груза может быть осуществлена шестью дорогами. Сколькими способами менеджер может составить маршрут для двух машин, если они должны ехать различными путями?
2. На кафедре работает 4 профессора. Они должны прочесть 2 лекции, причем один человек может прочитать обе лекции. Порядок прочтения лекций важен. Сколькими способами можно отобрать кандидатов для прочтения лекций?
3. Студент выучил 17 экзаменационных билетов, а 8 оставшихся не выучил. Какова вероятность, что студент не получит «двойку» (А), что получит «двойку» (B)?
4. В стандартной колоде 36 карт. Из четырех тузов разных мастей извлекается один, запоминается, затем возвращается обратно. Затем извлекается вторая карта. Сколькими способами можно выбрать таким образом пару тузов?
𝐴5𝑥+1− 𝐴3𝑥
5. Решить уравнение: 𝐴3𝑥 = 4.
6. Решить уравнение: 𝐶𝑥2+1 = 36.
7. Решить уравнение: 6𝐶𝑥3 = 11𝐴2𝑥−1.
8. Имеется 4 карточки с буквами В, С, А, Я. Какова вероятность того, что студент, извлекая по одной карточке, сможет сложить из них свое имя? Как зовут студента?
9. В урне находится 17 шаров: 9 белых, остальные – черные. Какова вероятность того, что первый, извлеченный из урны шар будет белый, а следующий черный?
10. Студенту на контрольной работе предложили 8 конвертов с заданиями. Из них 6 конвертов содержат простые задания, остальные – сложные. Какова вероятность того, что, случайным образом выбирая конверты, студент сначала возьмет конверт с простым, а затем со сложным заданием?
11. Вероятность того, что транзистор имеет скрытые дефекты, равна 0,25. На склад поступило 30 транзисторов. Какое событие вероятнее: что в этой партии имеется 4 транзистора со скрытыми дефектами или 5?
12. Устройство состоит из 800 элементов, работающих независимо один от другого. Вероятность отказа любого элемента равна 0,003. Найти вероятность того, что за время Т откажут 10 элементов.
13. Вероятность рождения мальчика равна 0,65. Найти вероятность того, что среди 100 новорожденных окажется ровно 50 мальчиков.
14. Игральную кость бросают 4000 раз. Какова вероятность того, что число очков, простое, выпадает не менее 1800 и не более 2200 раз?
15. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,5, для второго - 0,7 для третьего - 0,8. Случайная величина Х - число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения случайной величины.
16. Три стрелка стреляют по мишени. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,5, для второго-0,8, для третьего -0,7. Случайная величина Х- число попаданий в мишень, если стрелки делают по одному выстрелу. Найти закон распределения,
𝑀(𝑋), 𝐷(𝑋).
17. Составить матрицу смежности и инцидентности, список дуг и смежности для данного графа.
Какие степени вершин графа?
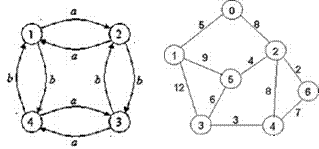
18. Опишите основные характеристики графа:
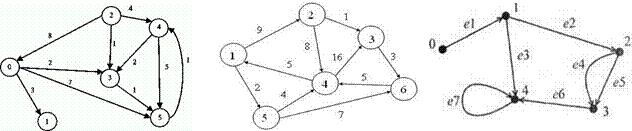
19. Между девятью планетами Солнечной системы установлено космическое сообщение. Рейсовые ракеты летают по следующим маршрутам: Земля — Меркурий, Плутон — Венера,
Земля — Плутон, Плутон — Меркурий, Меркурий — Венера, Уран — Нептун, Нептун — Сатурн, Сатурн — Юпитер, Юпитер — Марс и Марс — Уран. По каждому маршруту ракеты летают в обе стороны. Можно ли долететь на рейсовых ракетах от Земли до Марса?
20. Для графа, заданного матрицей смежности: найти матрицу инцидентности; построить граф; составить список дуг, проверить на наличие циклов, найти степень входа и выхода вершин графа.
1 2 3 4 5 6 1 2 3 4 5 6 1 2 3 4 5 6
|
|
1 |
1 |
1 |
|
1 |
1 2 3 4 5 6 |
|
1 |
|
1 |
|
1 |
1 2 3 4 5 6 |
|
1 |
1 |
|
|
1 |
|
1 |
|
1 |
|
|
1 |
|
|
1 |
|
1 |
|
|
|
1 |
1 |
1 |
|
||
|
1 |
1 |
|
1 |
1 |
1 |
|
|
|
1 |
|
1 |
|
|
|
|
1 |
1 |
||
|
1 |
|
1 |
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
1 |
|
||
|
|
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
1 |
||
|
1 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1
2
3
4
5
6
21. Найти кратчайшие расстояния от 1-й вершины до всех остальных для графа, представленного на рисунке и найти минимальное отставное дерево (использование алгоритма Краскала).
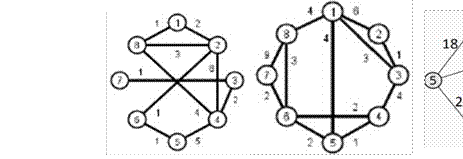
22. Для взвешенного неориентированного графа решить задачу коммивояжера (подробный ход решения).
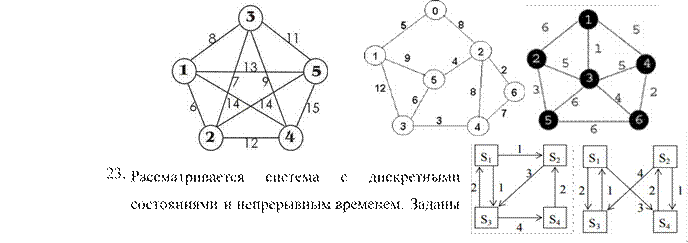
размеченный граф состояний и интенсивности переходов. Все потоки событий простейшие. Составить матрицу интенсивностей переходов. Найти предельное распределение вероятностей состояния.
24. Найти предельные вероятности для системы S, граф которой изображен на рисунке, где 𝜆01 = 1, 𝜆12 = 4, 𝜆23 = 5, 𝜆10 = 2, 𝜆21 = 2, 𝜆23 = 3.
𝜆01 = 2, 𝜆12 = 3, 𝜆23 = 4, 𝜆10 = 1, 𝜆21 = 2, 𝜆23 = 2.
𝜆01 = 3, 𝜆12 = 1, 𝜆23 = 3, 𝜆10 = 2, 𝜆21 = 2, 𝜆23 = 1.
 10 λ21 λ32
10 λ21 λ32 25. Сборочный участок работает с интенсивность потока 1,5 блоков в минуту. На этом участке работает контролер, который выборочно проверяет изготовленные блоки аппаратуры, средняя продолжительность контрольных операций равна 1,25 минут. Если в момент прибытия очередного блока контролер занят, то этот блок сразу же передается на дальнейшие операции без промежуточного контроля. Производство непрерывное и продолжается до обнаружения дефекта в одном из блоков, в этом случае технологический процесс останавливается, и выясняются причины неисправности. Определите основные показатели эффективности сборочного участка.
26. В мастерской по ремонту компьютеров в понедельник работает только один мастер, который выполняет заказ в среднем за 25 мин. Клиенты заходят в мастерскую в среднем каждые 35 мин и в случае занятости мастера уходят. Определите основные показатели эффективности мастерской.
27. Дайте оценку работы предприятия, если у нее имеется 6 каналов связи, за один час поступает в среднем 200 телефонных звонков, среднее время ответа на звонок - 0,8 мин.
28. В типографию с тремя множительными аппаратами поступают заказы от соседних предприятий на размножение рабочей документации. Если все аппараты заняты, то вновь поступающий заказ не принимается. Среднее время работы с одним заказом составляет 2 часа. Интенсивность потока - 0,5 заявки в час. Определите основные показатели эффективности типографии.
29. На станцию технического осмотра автомобилей, имеющего 3 смотровых поста, в среднем поступает 1 автомобиль за 0,4 часа. Стоянка во дворе вмещает 3 машины. Среднее время работы одного поста - 0,5 часа. Определить характеристики работы СТО.
30. Авто заправочная станция имеет одну бензоколонку. Предполагается что простейший поток автомашин поступает на станцию с интенсивностью 11 автомашин/ч. Время обслуживания заявки случайная величина которая подчиняется экспоненциальному закону с параметром 14 автомашин/ч. Определить среднее число автомашин на станции.
31. В расчетном узле магазина самообслуживания работает три кассы. Интенсивность входящего потока составляет 5 покупателей в минуту. Интенсивность обслуживания каждым контролером-кассиром составляет 2 покупателя в минуту. Определить характеристики СМО и дать оценку ее работы.
32. В многоканальную СМО с тремя каналами обслуживания поступают заявки с интенсивностью 0,7 заявок в час. (Поток заявок простейший). Поток обслуживания имеет интенсивность 0,4 заявки в час. Очередь заявок на обслуживание может расти практически неограниченно. Определите все средние характеристики системы.
33. Железнодорожную станцию обслуживает касса с одним окном. В летние выходные дни интенсивность потока пассажиров к кассе составляет 0.45 человек в минуту. Кассир затрачивает на облуживание пассажира в среднем 2 мин. Определите основные показатели станции.
34. К базе данных сервера продажи билетов поступает 10 запросов в секунду. Среднее время обработки каждого запроса составляет 1 секунду. Запрос, поступивший в момент обработки одного из ранее поступивших запросов, становится в очередь. Определите основные показатели сервера.
35. В расчетном узле магазина самообслуживания работает три кассы. Интенсивность входящего потока составляет 5 покупателей в минуту. Интенсивность обслуживания каждым контролером-кассиром составляет 2 покупателя в минуту. Определить характеристики СМО и дать оценку ее работы.
36. В многоканальную СМО с четырьмя каналами обслуживания поступают заявки с интенсивностью 2,5 заявок в час. (Поток заявок простейший). Поток обслуживания имеет интенсивность 1,5 заявки в час. Очередь заявок на обслуживание может расти практически неограниченно. Определите все средние характеристики системы.
37. Интенсивность потока телефонных звонков в агентство по заказу железнодорожных билетов, имеющему один телефон, составляет 16 вызовов в час. Продолжительность оформления заказа на билет равна 2.4 минуты. Определить относительную и абсолютную пропускную способность этой СМО и вероятность отказа (занятости телефона). Сколько телефонов должно быть в агентстве, чтобы относительная пропускная способность была не менее 0,75.
38. Система массового обслуживания — билетная касса с одним окошком и неограниченной очередью. Касса продает билеты в пункты А и В. Пассажиров, желающих купить билет в пункт А, приходит в среднем трое за 20 мин, в пункт В — двое за 20 мин. Поток пассажиров простейший. Кассир в среднем обслуживает трех пассажиров за 10 мин. Время обслуживания — показательное. Вычислить финальные вероятности Р1, P2, P3, среднее число заявок в системе и в очереди, среднее время пребывания заявки в системе, среднее время пребывания заявки в очереди.
39. Междугородный переговорный пункт имеет четыре телефонных аппарата. В среднем за сутки поступает 320 заявок на переговоры. Средняя длительность переговоров составляет 5 мин. Длина очереди не должна превышать 6 абонентов. Потоки заявок и обслуживаний простейшие. Определить характеристики обслуживания переговорного пункта в стационарном режиме (вероятность простоя каналов, вероятность отказа, вероятность обслуживания, среднее число занятых каналов, среднее число заявок в очереди, среднее число заявок в системе, абсолютную пропускную способность, относительную пропускную способность, среднее время заявки в очереди, среднее время заявки в системе, среднее время заявки под обслуживанием).
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.