Конкурсные задания для участия в республиканской олимпиаде Олимпиада по физике (1 этап)

Министерство образования республики Башкортостан

Государственное бюджетное профессиональное образовательное учреждение Зауральский агропромышленный колледж

Конкурсные задания

 для участия в республиканской олимпиаде

Олимпиада по физике (1 этап)

Разработал преподаватель:

Кашкаров Р.А.

Баймак 2016 г.

Олимпиада по физике (1 этап)

1.

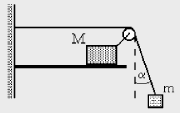
     В системе, изображенной на рисунке, брусок массой M может скользить по рельсам без трения. Груз отводят на угол a от вертикали и отпускают. Определите массу груза m, если угол a при движении системы не меняется.

2.

     Внутри длинной трубы, наполненной воздухом, двигают с постоянной скоростью поршень. При этом в трубе со скоростью S = 320 м/с распространяется упругая волна. Считая перепад давлений на границе распространения волны равным P = 1000 Па, оцените перепад температур. Давление в невозмущенном воздухе P₀ = 10⁵ Па, температура T₀ = 300 К.

3.

Пилот космического корабля, движущегося со скоростью V₀ = 1 км/c, заметил прямо по курсу астероид диаметром D = 7 км, когда до его поверхности осталось расстояние L = 8,5 км. Космонавт сразу же включил аварийные двигатели, которые за пренебрежимо малое время сообщают кораблю скорость U = 300 м/с, направление которой космонавт выбирает самостоятельно. Сможет ли корабль избежать столкновения с астероидом?

4.

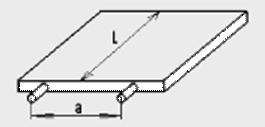
В серванте имеется выдвижная доска для резанья на ней хлеба. К доске спереди приделаны две ручки на расстоянии a друг от друга, симметрично относительно середины. Длина доски (в глубь серванта) равна L. При каком наименьшем значении коэффициента трения k между боком доски и стенкой серванта нельзя вытащить доску, действуя на одну из ручек, как бы ни была велика приложенная сила?

5.

Цилиндр прикреплен вверх дном к стенке открытого сосуда с водой. Верхняя часть цилиндра заполнена воздухом, давление которого равно атмосферному. Высота дна цилиндра над уровнем воды h = 1 см. Вода имеет температуру t₀ = 0^°C. На сколько сместится уровень воды в цилиндре, если воду и воздух нагреть до 100^°C (но не доводить воду до кипения)? Тепловым расширением воды и цилиндра, а также давлением водяного пара при t = 0^°C пренебречь. Сосуд широкий.

6.

Молодые люди решили на Новый год угостить своих друзей коктейлем со льдом и 31 декабря в 23.00 поставили ванночку с водой в морозильник. Через t1 = 15 мин они заглянули в морозильник и обнаружили, что за это время температура воды понизилась с 16ºС до 4ºС. Успеет ли замерзнуть вся вода до наступления Нового года? Когда же будет готов лед? Удельная теплоемкость воды c = 4,2·103 Дж/(кг·ºС), удельная теплота плавления льда  λ = 3,35·105 Дж/кг.

7.

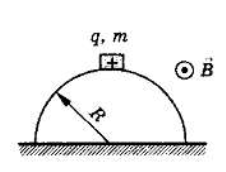
     Небольшое тело массой m, имеющее положительный заряд q, начинает скользить с вершины гладкого полуцилиндра радиусом R. На какой высоте, считая от основания полуцилиндра, тело оторвется от него? Движение происходит в однородном магнитном поле с индукцией B, направленной перпендикулярно плоскости чертежа к наблюдателю.

8.

Известно, что, благодаря антикрыльям, вес болида Формулы-1 при скорости v = 216 км/ч в 6 раз превышает силу тяжести. Определите, чему равен минимальный радиус поворота R , по которому способен проехать такой болид на данной скорости. Коэффициент трения между покрышками и поверхностью трассы равен m = 0,8. Ускорение свободного падения считайте равным 2 g =10 м/с .

9.

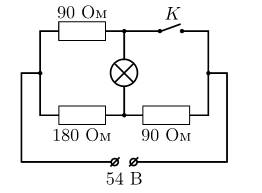
В собранной схеме (см. рисунок) лампочка горит одинаково ярко как при замкнутом, так и при разомкнутом ключе К. Найдите напряжение на лампочке.

10.

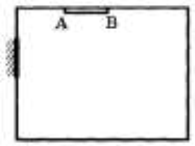
В каких точках комнаты должен находиться человек, чтобы видеть в зеркале экран телевизора АВ (см. рисунок) целиком?

Решения олимпиадных задач по физике

1.

Пусть T - сила натяжения нити, a₁ и a₂ - ускорения тел массами M и m.

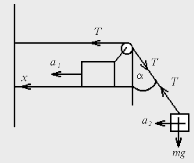
Записав уравнения движения для каждого из тел вдоль оси x, получим
a₁M = T·(1-sina),  a₂m = T·sina.

Поскольку при движении угол a не меняется, то a₂ = a₁(1-sina). Легко видеть, что

Отсюда

2.

Пусть волна движется в трубе с постоянной скоростью V. Свяжем эту величину с заданным перепадом давления DP и разностью плотностей Dr в невозмущенном воздухе и волне. Разность давлений разгоняет до скорости V "избыток" воздуха с плотностью Dr. Поэтому в соответствии со вторым законом Ньютона можно записать

Отсюда

Воспользуемся теперь уравнением Менделеева-Клапейрона, записав его в форме

Если считать Dr и DT малыми, то произведением Dr·DT можно пренебречь, и потому

Поделив последнее уравнение на уравнение P₀ = R rT₀ / m, получим

Поскольку Dr = DP/V², r = P₀m/(RT), окончательно находим

Численная оценка с учетом данных, приведенных в условии задачи, дает ответ DT » 0,48K.

3.

Из треугольника расстояний рассчитаем угол a, который нужно "превысить", чтобы корабль не столкнулся с астероидом:

Из треугольника скоростей найдем максимальный угол, под которым может двигаться корабль при оптимальной ориентации аварийных двигателей:

откуда

Поэтому в принципе катастрофы можно избежать.

Замечание: Если дополнительную скорость U направить перпендикулярно основной V, то tg a₀ = U/V,  a₀ = 16,7^°, т.е. a₀ = a. В этом случае произойдет столкновение.

4.

Пусть сила F приложена к левой ручке доски.

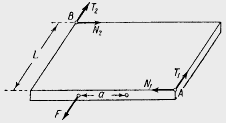
Эта сила вызывает в точках A и B реакции стенок серванта. Каждую из этих реакций можно разложить на составляющие N₁, N₂, нормальные к стенкам серванта, и T₁, T₂, касательные к тем же стенкам (силы трения). Предполагая, что доску вытащить нельзя, мы должны сделать следующие предположения:

1) сила F должна быть равна сумме сил трения, чтобы не было поступательного движения доски, т. е. F = T₁+T₂;

2) момент силы F относительно центра доски должен быть равен сумме моментов нормальных реакций относительно того же центра доски, чтобы не было вращения доски, т. е.

Кроме того, по определению имеем

Исключая из уравнений силу F, получаем, что наименьшее значение коэффициента трения должно равняться L/a. При большем его значении вытащить доску из серванта, действуя на одну из ручек, невозможно.

5.

Насыщенный пар при 100^°С создает давление, равное атмосферному: P₀ = 10⁵ Па. Из уравнения Менделеева-Клапейрона получаем

где P - давление воздуха под цилиндром при 100^° C, T₀ = 273 K, T = 373 K, x - искомое смещение уровня воды. Равенство давлений на глубине x под водой дает уравнение P₀+P = P₀+rgx, где r - плотность воды. Учитывая, что P₀ = rgH и H = 10³ см, получаем уравнение:

Решив это уравнение, находим

6.

Для охлаждения воды на ΔT1 = 16ºС - 4ºС = 12ºС от неѐ было отведено количество тепла, равное Q1 = сmΔT1. Будем считать, что морозильник работает непрерывно и скорость отвода тепла в нем постоянна. По условиям задачи известно время охлаждения воды, поэтому можно рассчитать скорость теплоотвода: q = Q1/ t1 = сmΔT1/ t1. Тогда время t2, необходимое для дальнейшего охлаждения воды от 4ºС до 0ºС, т.е. на ΔT2 = 4ºС, будет равно t2 = Q2/q = сmΔT2t1 / сmΔT1 = t1 ΔT2/ ΔT1. Подставив численные

значения, получим t2 = 5 мин, а время t3 необходимое для превращения в лед всей воды, находящейся при 0ºС, составит

 t3 = Q3/q = mλ t1/ сmΔT1 = λ t1/ сΔT1. t3 =100 мин.

Таким образом, время необходимое для приготовления льда, от момента постановки воды в морозильник до ее полного замерзания составит

t = t1 + t2 + t3 = 120 мин = 2 ч.

Ответ. Вода не успеет замерзнуть к Новому году, а замерзнет 1 января в 1 час 00 мин.

7.

Тело будет ускорено двигаться под действием сил: тяжести mg, реакции опорыN ,центробежной силы F ц, а также силы Лоренца Fл

Заметим, что возможны два варианта:

1) если тело скатывается в правую сторону, то сила Лоренца Fл

будет направлена по радиусу к центру цилиндра,

2) если тело скатывается в левую сторону, то сила Лоренца Fл

будет направлена по радиусу от центра цилиндра . Пусть в некоторой точке С тело отрывается от полуцилиндра, тогда в этой точке сила реакция опоры  N=0

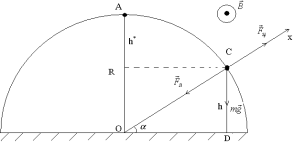
Проведем ось Ох как показано на рисунке. Поскольку в момент отрыва тело не движется вдоль этой оси, то сумма проекции всех сил на эту ось равна нулю:

                                 Ох: m Fл mg sin Fц 0 .

Перед силой Лоренца знак ―–‖ соответствует первому случаю, знак +‖ второму случаю. Учитывая, что Fл= qVB,

                                                       Fц man =mV²/R, sin= h/ R имеем

                                       m qVB mgh/R+mV²/R=0

Здесь V скорость тела в точке С. Закон сохранения энергии дает

                                        MgR= mgh+  mV²/2

Т.о. находим скорость в точке С:

                                        V ²=2g (R- h) . (2)

Подставляя (2) в (1) получаем уравнение, из которого находим h:

                               H=2/3R-qbr/9mg (qBR/m+--

Знак «+» перед корнем соответствует первому случаю, знак «--»  второму случаю.

8.

При движении болида в повороте центростремительное ускорение создаётся силой трения. Запишем второй закон Ньютона:

 mv²/ R = F тр

 Если поворот минимального радиуса, то модуль силы трения максимален и равен                                               F тр =mN .

На такой скорости сила реакции опоры

                                                     N =P = 6mg  .

Получим ответ: R = v² /6m g = 75 м.

9.

Решение:

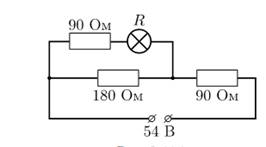
Обозначим сопротивление лампочки через R, а искомое напряжение на ней – через U. Исходную электрическую цепь с незамкнутым ключом можно изобразить в эквивалентном виде, показанном на рисунке . Тогда напряжение на участке цепи, содержащем параллельное соединение, равно

U₁ = U + 90 × (U/R), сила текущего через этот участок тока составляет

(U/R) + (U₁/180), и закон Ома для данной схемы дает:

U + 90 ×  + 90 × (+ 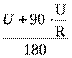) = 54.

После замыкания ключа цепь можно перерисовать, как показано на рисунке. Из него видно, что напряжение на верхнем участке цепи, содержащем два резистора и лампочку, составляет 54 В. Закон Ома для участка цепи имеет вид: U + 180 × (+ ) = 54.

Решая полученные уравнения, найдем, что сопротивление лампочки равно

R = 30 Ом, а напряжение на ней U = 6 В.

Ответ: 6 В.

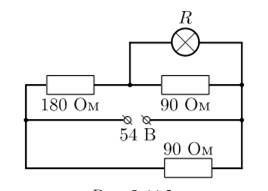
10.

    Применяя закон отражения, построим изображение экрана (A1B1) в зеркале (см. рисунок). Вертикальной штриховкой отмечена область, откуда можно видеть в зеркале отражение точки А; горизонтальной штриховкой соответствующая область для точки В. Из области, отмеченной двойной

штриховкой, можно видеть отражения точек А и Б, а, значит, и всего экрана телевизора.

Ответ: Искомая область (область, из любой точки которой будет видно все изображение экрана) отмечена двойной штриховкой.