КОНСПЕКТ УРОКА " ИНТЕРФЕРЕНЦИЯ, ДИФРАКЦИЯ"1 КУРС СПО

Конспект урока "Поляризация света"

  

 «Природу нельзя застигнуть неряшливой и

полураздетой, она всегда прекрасна»

Р.У. Эмерсон

В прошлых темах говорилось о двух явлениях, которые явно доказывают, что свет обладает волновыми свойствами — это интерференция и дифракция света.

Интерференция света — это явление сложения двух и более когерентных волн, приводящее к образованию в пространстве устойчивой картины чередующихся максимумов и минимумов интенсивности света.

Дифракция — совокупность оптических явлений, обусловленных волновой природой света и наблюдающихся при его распространении в среде с резко выраженными неоднородностями. В результате происходит огибание волнами препятствий, размеры которых соизмеримы с длиной волны.

В данной теме будет рассмотрено еще одно важное свойство света, которое состоит в том, что свет может быть поляризован.

Возникнет вопрос: а что значит поляризован и вообще, что такое поляризация? В рамках данной темы будут даны ответы на эти вопросы.

Поляризация происходит от латинского слово «полус» — конец оси, полюс. Применительно к свету термин «поляризация» впервые ввел Исаак Ньютон.

Под поляризацией понимают характеристику поперечных волн, описывающую поведение вектора колеблющейся величины в плоскости, перпендикулярной направлению распространения волны.

Рассмотрим данное явление на примерах механических моделей.

Поплавок на поверхности воды качается вверх вниз, но при этом не перемещается вместе с волнами. Значит, вдоль направления распространения волн перемещаются не сами частицы вещества, а создаваемые ими возмущения. Напомним, что в 9 классе такие волны назвались поперечными.

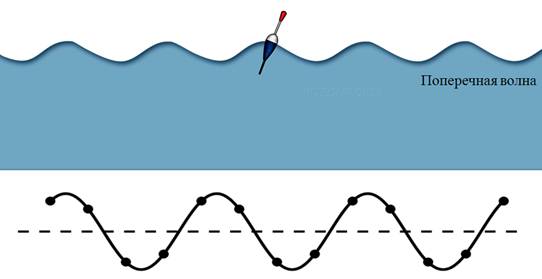
Рассмотрим еще пример. Возьмем веревку, один конец которой закрепим к стене, и будем рукой создавать в ней колебания. Как можно видеть, колебания веревки происходят с разными амплитудами и в разных направлениях. Однако если такую веревку пропустить через узкую щель, то такая щель будет выделять из неполяризованной волны единственное направление колебаний, параллельное щели.

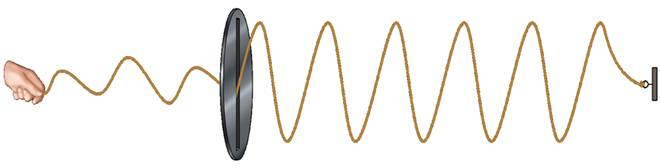
Теперь поставим на пути волны второй поляризатор с такой же щелью. Волна, выйдя из первой щели, свободно проходит через вторую, когда они параллельны.

Если же повернуть вторую щель, перпендикулярно первой, то волна полностью гасится.

Таким образом, в поляризованной волне существует выделенное направление колебаний.

Такую волну называют плоско поляризованной. Т.е. поперечная волна называется плоско поляризованной, если колебания во всех ее точках происходят только в одной плоскости.

Прибор, превращающий неполяризованную волну в поляризованную, называют поляризатором. А прибор, позволяющий установить, поляризована или нет проходящая через него волна — анализатором.

Известно, что явления интерференции и дифракции не оставляют сомнений в том, что распространяющийся свет обладает свойствами волн. Однако долгое время ученые не моги определить, каких именно волн — продольных или поперечных?

Основатели волновой оптики Томас Юнг и Огюстен Жан Френель считали световые волны продольными, т.е. они, подобны звуковым волнам, для распространения которых необходимо наличие среды. В связи с этим, ученые и считали, что свет распространяется в некой упругой среде, названной ими светоносным эфиром. Однако подобная теория не могла объяснить, каким же образом тела могут двигаться в твердом эфире, не встречая при этом никакого сопротивления. Т.е., например, как тогда движется Земля вокруг Солнца?

Но постепенно накапливалось все больше и больше экспериментальных фактов, которые никак не удавалось объяснить на основании продольности световых волн.

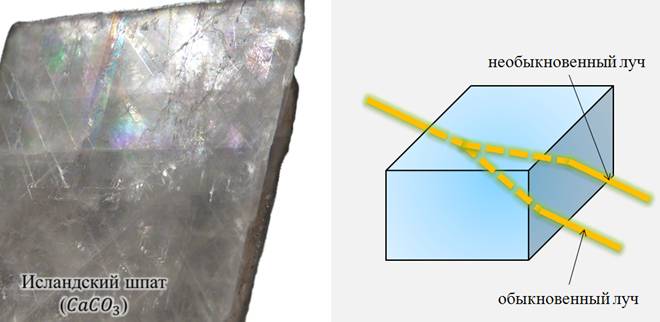
Например, еще в конце 17 века было обнаружено интересное явление: если пропустить луч света через кристалл исландского шпата (химическая формула CaCO₃), то на выходе из кристалла обнаруживалось 2 луча. При этом, если кристалл поворачивать относительно направления первоначального луча, то поворачиваются оба луча, прошедшие через кристалл. Это явление получило название двойного лучепреломления.

Немного позже, а точнее в 1809 году, французский инженер Этьен Луи Малюс поставил опыт, позже ставший классическим опытом по поляризации света, с кристаллами турмалина. Турмалин, как и исландский шпат, относится к числу одноосных кристаллов.

Из кристалла турмалина Малюс вырезал прямоугольную пластину так, чтобы одна из его граней была параллельна оси кристалла. После чего, перпендикулярно пластине направлялся пучок света. Если вращать пластину вокруг такого пучка, то никакого изменения интенсивности света не будет наблюдаться. Изначально Малюс решил, что свет только частично поглотился в турмалине и приобрел слегка зеленоватую окраску, а больше ничего, кажется, и не произошло.

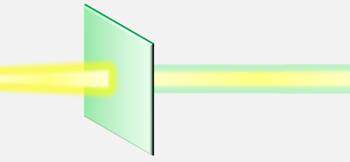
Однако это было не так — теперь свет приобрел свои новые свойства. И эти свойства можно обнаружить, если заставить пучок света пройти через еще одну, точно такую же прямоугольную пластинку турмалина, параллельную первой.

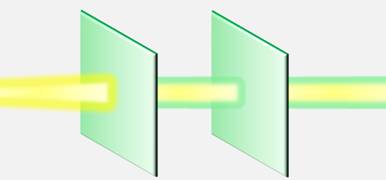
Малюс заметил, что если оси кристаллов будут одинаково направлены, то опять никаких существенных изменений в световой волне не наблюдается. Но стоит начать поворачивать второй кристалл, как тут же обнаруживается удивительное явление — происходит гашение света. При этом, чем больше будет угол между осями кристаллов, тем меньше будет интенсивность проходящего света. В конце концов, когда оси двух кристаллов окажутся перпендикулярны друг другу, свет не проходит совсем.

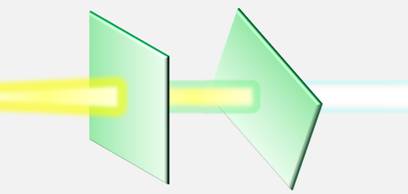
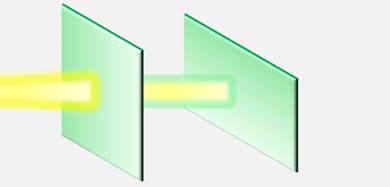
Из проделанного опыта, Малюс сделал два вывода.

Во-первых, световая волна, идущая от источника света, полностью симметрична относительно направления распространения (вспомните, в первой части опыта интенсивность света не менялась, при вращении кристалла вокруг луча); а во-вторых, волна, вышедшая из первого кристалла, не обладает осевой симметрией (это свидетельство из второй части опыта, когда интенсивность прошедшего света менялась).

Объяснить опыт с вращением второй пластины, считая световую волну продольной, не представляется возможным, т.к. продольные волны обладают полной симметрией по отношению к направлению распространения.

Таким образом, можно сделать вывод о том, что свет является поперечной волной. Позже это показал и Максвелл, дополнив это утверждение тем, что свет является не только поперечной, но еще и электромагнитной волной.

Свет, излучаемый каким-либо источником, представляет собой суммарное электромагнитное излучение множества атомов. Атомы, в свою очередь, излучают световые волны независимо друг от друга, поэтому световая волна, излучаемая телом в целом, характеризуется всевозможными равновероятностными направлениями колебаний светового вектора напряженности (т.к во всех процессах взаимодействия света с веществом основную роль играет именно он, поэтому его еще называют световым вектором).

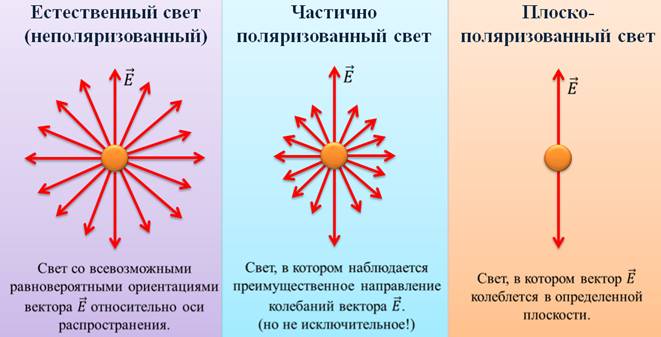
Свет со всевозможными равновероятными ориентациями вектора напряженности относительно оси распространения называется естественным или неполяризованным светом.

Свет, в котором наблюдается преимущественное направление колебаний вектора напряженности (но не исключительное!) называют частично поляризованным.

А вот свет, в котором вектор напряженности колеблется в определенной плоскости, называется плоско- или линейно поляризованным.

Можно, также заставить вектор напряженности при колебаниях описывать окружность или эллипс. Тогда в первом случае свет называется поляризованным по кругу, а во втором — эллиптически поляризованным.

В настоящее время известно, что не только кристаллы турмалина способны поляризовать свет. Таким же свойством, например, обладают так называемые поляроиды.

Поляроид представляет собой тонкую (около 0,1 мм) поляризационную плёнку, например кристаллов гепатита, нанесенную на целлулоид или стеклянную пластинку, которая заклеена между двумя прозрачными плёнками для защиты от влаги и механических повреждений.

Преимущество поляроидов состоит в том, что можно создавать большие поверхности, поляризующие свет.

К недостаткам можно отнести то, что поляроиды придают фиолетовый оттенок белому свету.

В настоящее время, явление поляризации электромагнитных волн находит огромное применение как в науке и технике, так и в повседневной жизни человека. Например, в трехмерном кинематографе оно используется для разделения изображения для левого и правого глаза.

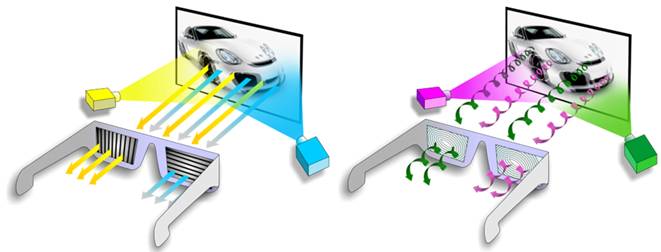
В обычной видео- и фотоаппаратуре поляризационные фильтры используются для улучшения качества изображения.

Также на качественные солнечные очки наносится поляризационная пленка, для того чтобы избавиться от бликов, которые получаются при отражении света. Современные жидкокристаллические экраны телевизоров, мониторов и мобильных телефонов также покрыты поляризационными пленками. В машиностроении и строительной индустрии явление поляризации используют для исследования напряжений, возникающих в узлах машин и строительных конструкций.

Многие насекомые в отличие от человека видят поляризацию света. Пчелы и муравьи пользуются этой своей способностью для ориентировки в тех случаях, когда Солнце закрыто облаками.

Любопытные поляризационные эффекты наблюдаются и при редких небесных оптических явлениях, таких, как радуга и гало — светящихся кругов или дуг, появляющихся иногда вокруг Солнца и Луны.

Наконец, следует отметить, что поляризован и свет некоторых астрономических объектов. Наиболее известный пример — Крабовидная туманность в созвездии Тельца.

Основные выводы:

– Поляризацией света называется совокупность явлений, в которых проявляется свойство поперечности световых волн.

– Прибор, превращающий неполяризованную волну в поляризованную, называется поляризатором.

– Прибор, позволяющий установить, поляризована или нет проходящая через него волна, называется анализатором.

– Явление поляризации электромагнитных волн в настоящее время находит огромное применение как в науке и технике, так и в повседневной жизни человека.

Конспект урока "Дифракция света"https://www.youtube.com/watch?v=Aqth19k6vCM&feature=emb_logo

 

  

На прошлых уроках мы с вами знакомились с геометрической оптикой — разделом физики, в котором изучаются законы распространения света в прозрачных средах и законы его отражения от зеркальных поверхностей.

Как мы говорили с вами ранее, основным положением геометрической оптики является прямолинейность распространения света. Оно является основополагающим при построении изображений в оптических системах, объяснении образования тени и полутени, солнечного и лунного затмений.

Доказано, что если на пути пучка света поместить непрозрачный предмет, то на экране за ним образуется чёткая тень; если пучок света проходит сквозь отверстие, то на экране наблюдается чёткое светлое пятно, то есть прямолинейность распространения света подтверждена многочисленными экспериментами и нашим собственным жизненным опытом.

Однако от закона прямолинейного распространения света наблюдаются отклонения при его распространении в средах с резко выраженными неоднородностями. Причём отклонения существенно зависят от соотношения между длиной волны и размерами препятствий.

И действительно, стоя за углом дома, мы хорошо слышим, что едет автомобиль, хотя не видим его, поскольку находимся в области «тени». Получается, что звуковые волны как бы «заворачивают за угол», в то время как световым волнам этого сделать не удаётся.

Напомним, что явление огибания волнами препятствий, которое проявляется в отклонении направления распространения волн от прямолинейного, называется дифракцией.

При изучении дифракции механических волн мы с вами говорили, что для проявления дифракции размеры препятствий (или отверстий) должны быть меньше или сравнимы с длиной волны. Вот почему в рассмотренном нами примере звук мотора автомобиля смог «завернуть за угол», а свет, отражённый от автомобиля, — нет.

Первые упоминания о явлении дифракции света можно встретить в работах великого итальянца Леонардо да Винчи. Франческо Гримальди подробно описал его в 1665 году. Но лишь в самом начале XIX века учёные нашли объяснение этому явлению.

Итак, в 1802 году Томас Юнг ставит свой знаменитый опыт по наблюдению за интерференцией и дифракцией света. Напомним, что установке источником света служила ярко освещённая щель, от которой фронт волны падал на две узкие равноудалённые щели, параллельные первой. Возникшая в соответствии с принципом Гюйгенса сферическая волна от отверстия «А» возбуждала в отверстиях В и С когерентные колебания. Вследствие дифракции от этих отверстий выходили два световых конуса, которые частично перекрывались. Интерференционная картина наблюдалась на экране, расположенном параллельно щелям в области перекрытия волн. При этом в центре картины была расположена светлая полоса, а по краям радужные полоски в случае белого света, или чередование тёмных и светлых полос в случае света монохроматического. При этом Юнг обнаружил, что если закрыть одно из отверстий, то интерференционная картина исчезала.

Окончательное исследование дифракции света было завершено современником Юнга французским физиком Огюстеном Френелем при написании им конкурсной работы для Академии наук Франции. В начале Френель пытался объяснить явление дифракции с помощью принципа Гюйгенса, согласно которому, как мы помним, каждая точка, до которой доходит волна, является центром вторичных сферических когерентных волн. Огибающая же этих волн даёт положение нового фронта волны в следующий момент времени.

Однако, как оказалось, с помощью данного принципа можно решить задачу о направлении распространения волнового фронта, но нельзя выяснить, от чего же зависит амплитуда, и, как следствие, интенсивность волн, распространяющихся по разным направлениям. Поэтому Френелю пришлось развить этот принцип дальше, дополнив его идеей об интерференции вторичных волн. Таким образом, принцип Гюйгенса трансформировался в принцип Гюйгенса-Френеля, согласно которому, каждая точка фронта волны является источником вторичных сферических когерентных волн. Новый фронт волны образуется в результате интерференции вторичных волн.

Таким образом, согласно Френелю, дифракция света объясняется интерференцией вторичных волн от различных участков начального положения волнового фронта. А учёт амплитуд и фаз вторичных волн позволяет в каждом конкретном случае найти амплитуду, а, следовательно, и интенсивность результирующей волны в любой точке пространства.

Теперь давайте проведём такой опыт. Возьмём точечный источник монохроматического света, круглую диафрагму, диаметр которой можно изменять, и экран. Включив источник света при очень малом диаметре диафрагмы, мы наблюдаем на экране светлое пятно. Что же произойдёт, если увеличить диаметр отверстия. Как это не парадоксально, но в центре экрана мы увидим тёмное пятно — минимум интерференции. Ещё увеличим диаметр отверстия — дифракционная картина изменилась, а в её центре мы вновь наблюдаем максимум.

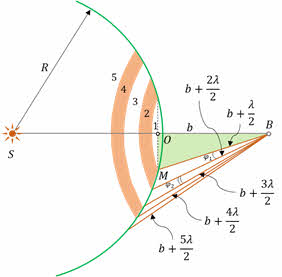
Для объяснения полученной дифракционной картины от круглого отверстия, Френель предложил разбить волновую поверхность на отдельные кольцевые зоны — зоны Френеля, — так, чтобы расстояние от соседних зон до точки наблюдения отличались ровно на половину длины волны. Диафрагма служит для того, что бы можно было ограничивать число действующих зон.

Если открыты только первые две зоны Френеля, то разность хода от них равна половине длины волны. Поэтому волны от этих зон приходят к экрану в противофазе и, как следствие, ослабляют друг друга. Поэтому в центре дифракционной картины мы наблюдаем тёмное пятно. Если же мы увеличим отверстие так, чтобы на освещённость экрана влияла ещё и третья зона, то в центре появляется светлое пятно. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если i — чётное, то в центре тёмное кольцо, если i нечётное — то светлое).

Следует учесть, что с увеличением номера зоны будет уменьшаться угол, под которым она видна из точки наблюдения. Вследствие этого уменьшаются и амплитуды волн:

Если принять, что первая зона вызывает в точке В колебания с амплитудой А₁, вторая — с амплитудой А₂ и так далее, то амплитуда колебаний в точке В будет определяться формулой, которую вы видите на экране:

Так как общее число зон Френеля, вмещающихся на полусфере радиусом, равным расстоянию от источника света до фронта волны, очень велико, то в первом приближении можно считать, что амплитуда колебаний от некоторой i-й зоны равна среднему арифметическому от амплитуд, примыкающих к ней зон:

Перепишем выражение для амплитуды колебаний в точке «Бэ» с учётом последнего уравнения:

Так как выражения, стоящие в скобках равны нулю, то амплитуда волны в центре дифракционной картины определяется полусуммой волн от первой и последней открытой зоны, когда их число нечётное. И их полуразностью при чётном числе зон Френеля.

Если считать, что общее число зон Френеля, вмещающихся на полусфере радиусом, равным расстоянию от источника света до фронта волны, очень велико, то A_i/2 ничтожно мала. Следовательно, амплитуда колебаний, создаваемая в произвольной точке сферической волновой поверхностью, определяется половиной амплитуды центральной зоны:

Теперь рассмотрим ΔМАО — он прямоугольный. Тогда используя теорему Пифагора, мы с вами легко можем определить радиус i-й зоны Френеля:

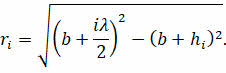
Упростим записанное равенство, учитывая, что h_i >> b и длина волны света мала:

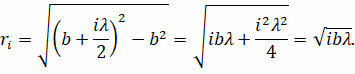
Отсюда находим, что радиус первой зоны Френеля определяется квадратным корнем из длины световой волны и расстоянием от фронта волны до экрана:

Учитывая, что длина световой волны может принимать значения от 300 нм до 860 нм, получим, что радиус первой зоны Френеля намного меньше расстояния от фронта волны до экрана. Это говорит нам о том, что распространение света от источника света до точки «Бэ» (В) происходит так, будто световой поток распространяется внутри очень узкого канала, диаметр которого меньше радиуса первой зоны Френеля, то есть прямолинейно.

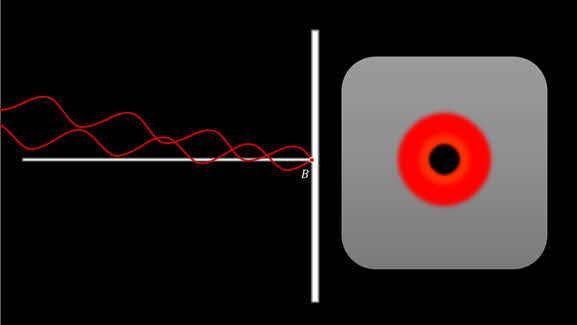
За свою конкурсную работу Огюстен Френель получил главный приз Академии наук Франции. Однако, некоторые учёные скептически отнеслись к работам Френеля, так как они послужили доказательством волновой теории света. В частности, член комиссии Пуассо́н обратил внимание на один парадоксальный результат: согласно Френелю за большим круглым непрозрачным телом прямо в середине его геометрической тени должно возникать небольшое светлое пятно:

Очевидную абсурдность этого результата Пуассон хотел использовать как главный аргумент против теории дифракции Френеля. Однако, другой член комиссии Доминик Франсуа Жан Араго поставил эксперимент, подтвердивший это предсказание. В итоге полученный результат, ставший известным как пятно Пуассона или пятно Араго — Пуассона, оказался весомым аргументом в пользу новой и более точной волновой теории света.

Волновая оптика показала, что все законы геометрической оптики выполняются достаточно точно лишь в том случае, если размеры препятствий на пути распространения света много больше длины световой волны. Но совершенно точно они не выполняются никогда.

Например, согласно законам геометрической оптики с помощью оптических микроскопов можно рассмотреть сколь угодно малые объекты (вплоть до атомов). А с помощью телескопов мы можем заглянуть в самые удалённые уголки Вселенной и установить существование не только звёзд, но и планетарных систем вокруг них. Однако в действительности это не так. И лишь волновая теория позволила разобраться в причинах предела разрешающей способности оптических приборов.

Разрешающей способностью прибора называется способность оптического прибора различать детали рассматриваемого объекта.

Волновая природа света налагает предел на возможность различать детали предмета или очень мелкие предметы при их наблюдении с помощью микроскопа. Дифракция не позволяет получить отчётливые изображения мелких предметов, так как свет распространяется не строго прямолинейно, а огибает предметы. Минимальное линейное расстояние между точками предмета или двумя предметами, которые можно различить с помощью микроскопа, определяется формулой, представленной на экране:

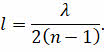
Если учесть, что показатель преломления стекла в среднем равен полутора, то получаем, что невозможно разрешить две детали объекта, размеры которых меньше длины световой волны:

Применение ультрафиолетового излучения позволяет повысить разрешающую способность линз. Использование же электронного микроскопа даёт возможность получать разрешение, во много раз превышающее разрешение оптического микроскопа.

Дифракция также налагает предел на разрешающую способность и телескопа. Вследствие дифракции волн у края оправы объектива изображением звезды будет не точка, а система светлых и тёмных колец. Если две звезды находятся на малом угловом расстоянии друг от друга, то эти кольца налагаются друг на друга, и глаз не может различить, имеются ли две светящиеся точки или одна. Предел разрешения оптического телескопа между светящимися точками, при котором их можно различать, определяется отношением длины волны к диаметру объектива:

Отсюда следует, что для уменьшения углового расстояния, которое разрешается телескопом, необходимо использовать объективы как можно большего диаметра.

Эти простые примеры показывают, что с дифракцией нужно считаться всегда, при любых препятствиях, и даже в случаях препятствий, размеры которых значительно больше, чем длина волны.

Конспект урока "Дифракционная решётка"

 

https://www.youtube.com/watch?v=3D7otlQNx24&feature=emb_logo

  

Для получения отчётливой дифракционной картины лучше использовать очень маленькие препятствия (например, тонкую проволоку, круглое отверстие или круглый экран), либо не располагать экран далеко от препятствий.

Однако чаще всего для получения дифракционной картины и измерения длины волны пользуются специальным прибором, который называется дифракционной решёткой.

Она представляет собой совокупность большого числа параллельных штрихов одинаковой формы, нанесённых на плоскую или вогнутую полированную поверхность на одинаковом расстоянии друг от друга.

Первая дифракционная решётка, сконструированная американским учёным Риттенхаузом, состояла из параллельного ряда волосков диаметром около 0,1 мм и длиной 10 мм, натянутых на расстоянии порядка 0,2 мм один от другого.

Лишь позже немецкий физик Йозеф Фраунгофер вместо волосков предложил использовать штрихи, наносимые на стекло алмазным острием. В его первой решётке число штрихов на 1 мм достигало 300.

В настоящее время принято различать отражательные дифракционные решётки и прозрачные.

В прозрачных дифракционных решётках штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране). Наблюдение ведётся в проходящем свете.

В отражательных решётках штрихи нанесены на зеркальную (металлическую) поверхность, и наблюдение дифракции ведётся в отражённом свете.

Если ширина прозрачных щелей (или отражающих свет полос) равна а и ширина непрозрачных промежутков (или рассеивающих свет полос) равна b, то величина, равная d = а + b называется периодом (или постоянной) решётки. Он показывает, сколько штрихов приходится на один миллиметр длины решётки:

Рассмотрим элементарную теорию дифракционной решётки.  Пусть на решётку, постоянная которой равна d, падает плоская монохроматическая волна, длина которой λ. Из принципа Гюйгенса следует, что волны, дифрагировавшие на щелях, распространяются за решёткой по всем направлениям.

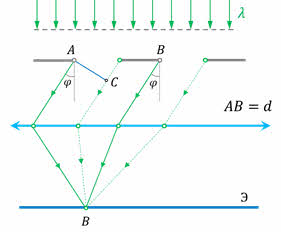
Для наблюдения дифракционной картины на экране между ним и решёткой размещают собирающую линзу таким образом, чтобы экран находился в фокальной плоскости линзы. Собирающая линза фокусирует на экране падающие на неё параллельные лучи (вторичные волны).

Допустим, что свет дифрагирует на щелях под углом φ. Так как щели находятся друг от друга на одинаковых расстояниях, то разности хода лучей, идущих от двух соседних щелей, для данного направления будут одинаковыми в пределах всей дифракционной решётки:

В зависимости от разности хода между вторичными волнами, испущенными разными щелями, они интерферируют друг с другом, усиливая или ослабляя друг друга. В тех направлениях, для которых разность хода равна чётному числу полуволн, наблюдается интерференционный максимум. В тех же направлениях, где разность хода равна нечётному числу полуволн, наблюдается интерференционный минимум. В итоге на экране мы наблюдаем дифракционную картину светлых и тёмных полос.

Таким образом, в направлениях, для которых углы удовлетворяют условию

наблюдаются главные максимумы дифракционной картины.

Эту формулу часто называют формулой дифракционной решётки. В ней k называется порядком главного максимума и может принимать значения ноль, один, два и так далее.

Из условия возникновения главных дифракционных максимумов следует, что при k = 0 для любых длин волн угол φ = 0. Следовательно, прямо по центру решётки образуется нулевой максимум, который называется также центральным максимумом. Остальные дифракционные максимумы образуют спектры первого, второго и так далее порядков.

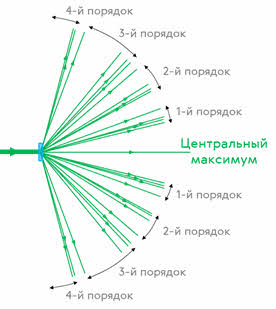
Естественно, что количество максимумов в дифракционной картине ограничено, поскольку синус не может принимать значения, больше единицы.

При падении на решётку белого света центральный максимум представляет собой изображение источника, так как в этом направлении собирается излучение всех длин волн. Все остальные максимумы оказываются окрашенными. Это объясняется тем, что, различным длинам волн соответствуют различные углы, на которых наблюдаются интерференционные максимумы:

Радужная полоска, содержащая в общем случае семь цветов — от фиолетового до красного (считается от центрального максимума), называется дифракционным спектром.

Ширина спектра зависит от постоянной решётки и увеличивается при её уменьшении. А максимальный порядок спектра определяется из условия, что «синус угла Фи» меньше либо равен единице:

Мы можем наблюдать дифракционную картину достаточно просто. Так, если прищуриться, смотря на яркий источник света, то можно обнаружить радужные цвета. Наши ресницы вместе с промежутками между ними представляют собой грубую дифракционную решётку. А лазерный диск с бороздками, проходящими близко друг от друга, подобен отражательной дифракционной решётке.

Для закрепления нового материала давайте с вами определим постоянную дифракционной решётки, если красная линия (λ = 7 ∙ 10^–7 м) в спектре второго порядка получается на расстоянии 25 см от центральной светлой полосы на экране. Расстояние от экрана до дифракционной решётки равно сорока трём целым трём десятым сантиметра (43,3 см).

Для удобства решения задачи будем считать, что дифракция наблюдается при нормальном падении на решётку параллельных лучей белого света.

Конспект урока "Дисперсия света"

  

Проведём небольшой эксперимент. Возьмём три одинаковые трёхгранные призмы и пропустим через них пучки монохроматического света различных цветов, например, красного, зелёного и фиолетового. Как видим, лучи фиолетового цвета испытают большее преломление по сравнению с зелёными.

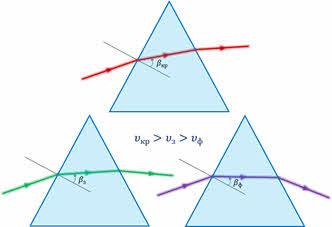
А лучи красного цвета преломляются меньше всего. Это говорит нам о том, что угол преломления красных лучей больше, чем для лучей зелёного и фиолетового цветов. Тогда, из закона преломления света следует, что красный свет в среде распространяется быстрее. Но поскольку цвет, воспринимаемый человеческим глазом, определяется только частотой световой волны, то цвет при переходе из вакуума в вещество или из одного вещества в другое не изменяется.

Зависимость скорости распространения световых волн в среде (или зависимость показателя преломления среды) от частоты (или длины волны) света называют дисперсией света.

Впервые подробно исследовал дисперсию света сэр Исаак Ньютон. До Ньютона считалось, что цвет тела — это свойство самого тела. Например, Аристотель объяснял наличие различных цветов смешением белого света с определённым количеством темноты: немного темноты, добавленной к свету, даёт красный свет; большее количество темноты — и вот мы уже видим фиолетовый свет. И эта теория господствовала в плоть до середины XVII века.

В 1666 году Исаак Ньютон, занимаясь усовершенствованием телескопов, обратил внимание на интересный факт: изображение, получаемое с помощью объектива телескопа, по краям было окрашено. Предполагая, что это может быть как-то связано с явлением преломления света, он поставил небольшой эксперимент, который детально описал в трактате «Оптика»: «Я поместил в очень темной комнате у круглого отверстия около трети дюйма шириной в ставне окна стеклянную призму, благодаря чему пучок солнечного света, входившего в это отверстие, мог преломляться вверх к противоположной стене комнаты и образовывал там цветное изображение Солнца состоящее из ряда цветных полос плавно переходящих друг в друга».

Следуя многовековой традиции, согласно которой радуга считалась состоящей из семи основных цветов, Ньютон тоже выделил семь цветов: фиолетовый, синий, голубой, зелёный, жёлтый, оранжевый и красный. Саму же радужную полоску Ньютон назвал спектром.

Казалось бы, простейший опыт Ньютона показал, что белый свет является сложным: пройдя через призму, он разлагается на пучки различных цветов.

Однако не все приняли результаты опыта — слишком уж необычным казалось это предположение. Основные вопросы сводились к следующему: почему белый свет, входящий в призму, выходил из неё в виде цветной полосы, содержащей именно семь цветов; почему круглый в сечении пучок после преломления в призме оказался существенно растянутым в длину; и, может это вещество, из которого изготовлена призма, окрашивает белый свет?

Для решения всех этих вопросов Ньютон провёл ещё несколько простых, но в то же время гениальных экспериментов. В начале он на пути пучка, прошедшего через призму, поместил собирающую линзу. Пройдя через неё пучок разноцветных лучей в точке схождения вновь становился белым. Такой же результат давала и вторая призма, повёрнутая на 180^о относительно первой. Таким образом было доказано, что свет действительно имеет сложную структуру.

Следующие опыты Ньютона были посвящены изучению влияния вещества призмы на характер окрашивания светового пучка. Закрыв отверстие красным стеклом, Ньютон наблюдал на стене только красное пятно, закрыв синим стеклом — синее пятно и так далее. Это означало, что не призма окрашивает белый свет, так как она не может влиять на цвет светового пучка.

Отдельные цветные лучи, которые после прохождения призмы не разлагались на составляющие, были названы простыми или монохроматическими.

Опытным путём Ньютон нашёл ответ и на ещё один важный вопрос: почему пучки разных цветов по-разному отклоняются призмой? В своём фундаментальном трактате «Оптика» Ньютон так сформулировал полученный им вывод: «Световые пучки, отличающиеся по цвету, отличаются по степени преломляемости. В наибольшей степени преломляются фиолетовые пучки, в наименьшей красные».

Однако и эти опыты не смогли убедить некоторых сторонников Аристотеля. Например, выдающийся немецкий поэт и видный естествоиспытатель Иоганн Гёте писал: «Утверждение Ньютона — это чудовищное предположение. Не может быть, что самый прозрачный, самый чистый цвет — белый — оказался смесью цветных лучей». Поэт считал, что исследованный Ньютоном свет — это свет, «замученный всякого рода орудиями пытки — щелями, призмами и линзами».

Друзья, избегайте тёмной комнаты,

Где вам искажают свет

И самым жалким образом

Склоняются перед искажёнными образами.

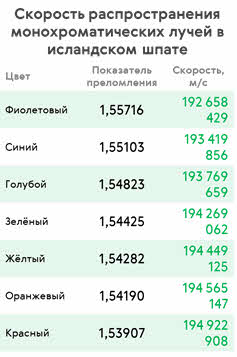
Ранее мы с вами показали, что показатель преломления среды зависит от скорости света в веществе. Следовательно, пучок фиолетового цвета преломляется в большей степени потому, что фиолетовый цвет имеет в веществе наименьшую скорость. Красные же лучи преломляются меньше других потому, что их скорость в веществе наибольшая. Это означает, что показатель преломления вещества, из которого сделана призма, зависит не только от свойств самого вещества, но и от частоты проходящего через него света.

С помощью дисперсии света объясняются многие явления природы, например, радуга. Она является одним из самых красивых явлений природы и поэтому поэтизировалась многими народами:

Как неожиданно и ярко,

На влажной неба синеве,

Воздушная воздвиглась арка

В своём минутном торжестве!

Один конец в леса вонзила,

Другим за облака ушла — Она полнеба обхватила

И в высоте изнемогла.

Фёдор Тютчев

Радуга возникает из-за того, что солнечный свет преломляется и отражается капельками воды, парящими в атмосфере. Эти капельки по-разному отклоняют свет разных цветов, в результате чего белый свет разлагается в спектр.

Наблюдатель, который стоит спиной к источнику света, видит разноцветное свечение, которое исходит из пространства по концентрическим окружностям (дугам). При этом радуга появляется только в том случае, если угловая высота Солнца над горизонтом не превышает 42^о.

Дисперсией света объясняется возникновение и такого явления, как гало. Его можно наблюдать зимой в виде кругов, столбов или крестов вокруг Солнца и Луны. Здесь дисперсия происходит в ледяных кристалликах на высоте около 10 км в верхних слоях тропосферы.

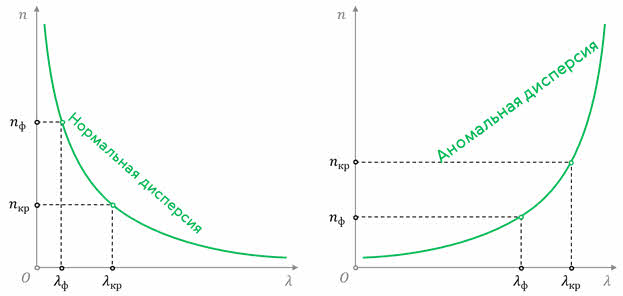
Дисперсия присуща всем средам, кроме вакуума. Её можно представить в виде зависимости показателя преломления вещества от частоты падающего света. Как показали различные опыты, для большинства веществ показатель преломления уменьшается с уменьшением частоты. Причём зависимость эта нелинейная. Дисперсию такого рода называют нормальной.

Однако в парах йода и в некоторых жидкостях учёные наблюдали и аномальную дисперсию. При такой дисперсии показатель преломления увеличивается с увеличением длины волны. Проще говоря, в них скорость распространения красных лучей меньше, чем фиолетовых.

В настоящее время, для получения хороших и ярких дисперсионных спектров используются специальные оптические приборы — спектроскопы и спектрографы. Первый спектроскоп был изобретён в 1815 году немецким физиком Йозефом Фраунгофером. Он состоял из окуляра, зрительной трубы, двух объективов, коллиматора и дифракционной щели.

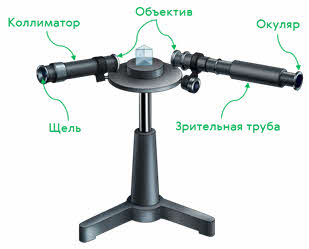
В оригинальном дизайне спектроскопа свет, прошедший через щель, расположенную в фокальной плоскости коллиматорной линзы, преобразовывался в тонкий световой пучок и попадал на призму. Из призмы выходят уже параллельные пучки разного направления, которые, преломившись в линзе зрительной трубы, образуют в её фокальной плоскости изображение щели. Если исследуется белый свет, то изображения щели сливаются в одну цветную полосу всех основных цветов. Если же исследуемый свет является монохроматическим, то спектр получается в виде узких линий, разделённых широкими тёмными промежутками.

Таким образом, с помощью призмы, как и с помощью дифракционной решётки, можно получить спектр некоторого излучения. Однако в дисперсионном и дифракционном спектрах имеются различия:

1) для дифракционного спектра можно создать равномерную шкалу по λ. Для дисперсионного спектра этого сделать нельзя, так как зависимость показателя преломления от длины волны является нелинейной функцией.

2) в дисперсионном спектре большее отклонение от первоначального направления испытывают фиолетовые лучи, в дифракционном же — красные.

3) в дифракционном спектре наблюдается несколько порядков спектра, в дисперсионном — один.

Итак, мы уже выяснили, что окружающий нас мир является красочным именно потому, что солнечный свет является сложным. Но всё же пока не ясно, почему же окружающий нас мир пестрит различными красками. И почему различные предметы, освещённые одним и тем же солнечным светом, имеют разный цвет?

Чтобы разобраться в этом, получим на экране спектр белого света. Теперь возьмём цветную бумажную полоску (например, зелёного цвета) и закроем ей часть спектра. Обратите внимание на то, что цвет полоски остался зелёным только в той области спектра, где на неё падают зелёные лучи. В жёлтой области спектра наша бумажка изменила оттенок. А в остальных частях спектра она выглядит тёмной.

Это говорит нам о том, что тела, имеющие зелёную окраску, способны отражать в основном лучи зелёного цвета, а остальные поглощают. Аналогично тела, имеющие красную окраску, в основном отражают красные лучи. Белые тела, которые освещаются дневным светом, в равной степени отражают лучи всех цветов, поэтому мы их и видим белыми. Чёрные же тела, наоборот, поглощают практически все падающие на них лучи. Что касается прозрачных тел, то их цвет обусловлен составом того цвета, который прошёл через них.

 

Скачано с www.znanio.ru