конспект урока "Геометрические фигуры" 5 класс

ОБЛАСТНОЕ ГОСУДАРСТВЕННОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ИВАНОВСКАЯ КОРРЕКЦИОННАЯ ШКОЛА-ИНТЕРНАТ№1»

Московская ул., д.44, г. Иваново, 153000 т.8(4932) 30-32-25

ОГРН 1023700547419 ОКПО 02083763 ОКАТО24401370000 ИНН/КПП3702011633/370201001

Конспект урока математики в 5 классе

по теме

«Геометрические фигуры»

Тип урока – обобщение и систематизация знаний с включением новых знаний.

Цели урока:

     - обучающие: повторить основные сведения о геометрических фигурах (углы, треугольники и др.); обобщить ранее накопленные знания о них; рассмотреть решение задач с использованием свойств углов, свойств и видов треугольников; рассмотреть пропедевтический материал о свойстве биссектрисы угла.

    - развивающие: развивать у учащихся умения анализировать задачу перед выбором способа ее решения; развивать навыки исследовательской деятельности, синтеза, обобщения;

     - воспитывающие: предоставить учащимся возможность осознать значимость себя, почувствовать уверенность в своих силах; воспитывать у учащихся личностную рефлексию: стал ли он сам для себя изменяющимся субъектом деятельности.

Технология проведения урока: технология деятельностного подхода

1. Методы проблемного обучения:

эвристический метод (постановка проблемы и организация совместной поисковой деятельности по её разрешению).

2. Методы организации учебно-познавательной деятельности:

 практические (закрепление практических умений и навыков происходит в ходе выполнения практических заданий), словесные. Выбранные методы оптимальны для данного урока и позволяют решить  задачу личностно-ориентированного подхода в обучении на этом уроке.

Оборудование и материалы: компьютер,  мультимедийный проектор, интерактивная доска. Урок проводится с использованием мультимедийной презентации Power Point, ресурса, созданного в программном обеспечении интерактивной доски.

Учебно-методическое пособие   под редакцией И.И. Зубаревой и А.Г. Мордковича.

Ход урока:

1. Оргмомент.

Настроить учащихся на деятельность, эмоционально ободрить их, снять напряженность, создать ситуацию комфорта.

2. Самоопределение к деятельности.

Учащимся предлагается ответить на вопросы по темам «Углы», «Треугольники»,

1.     Назовите единицу измерения углов.

2.     Как называется инструмент для измерения углов?

3.     Какая фигура называется углом?

4.     Что такое биссектриса угла?

5.     Чему равна сумма углов в треугольнике?

6.     Перечислите виды треугольников (классификация по сторонам и углам).

7.     Какова градусная мера прямого угла?

8.     Как найти площадь треугольника?

В завершении этого этапа урока учитель совместно с учениками формулирует тему урока («Геометрические фигуры»), формулирует основную задачу урока – повторить и обобщить все, что мы узнали об углах, треугольниках и других фигурах, сообщает учащимся о том, что сегодня на уроке мы исследуем и сформулируем одно замечательное свойство известной геометрической фигуры.

 Тему урока учащиеся записывают в тетрадях

3. Актуализация знаний.

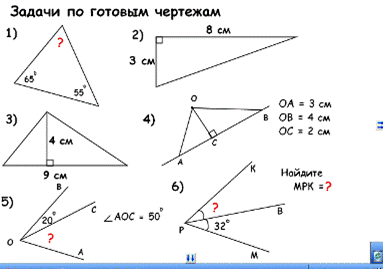На данном этапе урока учащиеся выполняют задания на готовых чертежах. Задания выполняются в основном устно, по необходимости учащиеся могут делать краткие вычислительные записи в тетрадях.

Чертежи к задачам появляются на экране интерактивной доски (ресурс «Геометрические фигуры», страница 2)

Задача 1. Найдите градусную меру третьего угла треугольника.

Задача 2. Вычислите площадь прямоугольного треугольника.

Задача 3. Вычислите площадь треугольника.

Задача 4. Найдите расстояние от точки О до прямой АВ.

Задача 5. Вычислите градусную меру угла АОС.

Задача 6. Чему равна градусная мера угла КРВ? Вычислите градусную меру угла МРК.

4. Повторение изученного ранее.

Учащимся предлагается решить ряд задач на повторение свойств равнобедренного треугольника, свойств углов, а также задачу на построение биссектрисы угла и перпендикуляров к прямым.

Задачи выведены на экран (ресурс «Геометрические фигуры», страница 3)

4. Открытие нового знания.

Учитель рассказывает учащимся историю о том, как поссорились Маша и Витя. Они оказались в поле, и решили пойти к одной из дорог, которые располагались вокруг них в виде треугольника.

(Картинка демонстрируется на интерактивной доске)

Мальчик и девочка не могли решить, к какой из дорог им пойти, где ближе. Учащимся предлагается попробовать им помочь (учитель отмечает, что сделать это можно лишь при определенных условиях).

Далее строится математическая модель задачи: дан треугольник, нужно найти такую точку внутри него, чтобы расстояние от нее до сторон треугольника было одинаково.

Учащимся предлагается вспомнить решение задачи № 3, еще раз продемонстрировать ее решение на интерактивной доске (с помощью заготовленных заранее страниц 7-10 ресурса «Геометрические фигуры»), отметить, что в ходе ее решения мы строили отрезки, которые определяют расстояние от точки, лежащей на биссектрисе угла, до сторон этого угла. Вместе с учащимися исследовать вопрос о равенстве таких отрезков. Программное обеспечение интерактивной доски позволяет подтвердить для учащихся данный факт, используя определение равных фигур (это фигуры, которые совпадают при наложении).

(Весь процесс исследования демонстрирует видеоприложение 2).

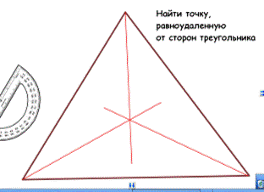В ходе дальнейшей беседы учащиеся делают вывод о том, что любая точка биссектрисы угла равноудалена от его сторон. А в треугольнике таких углов три. Значит можно предположить, что если построить все три биссектрисы, то мы, возможно, найдем внутри треугольника ту самую точку, которая поможет разрешить спор Маши и Вити.

Учитель строит на интерактивной доске три биссектрисы углов треугольника. И учащиеся убеждаются, что все они пересекаются в одной точке. Значит, спор детей окажется беспричинным, если они окажутся в этой точке. Поэтому, чтобы помирить Машу и Витю, мы переместим их именно в эту точку (ресурс «Геометрические фигуры», страница 11, на данной странице в левом верхнем углу за белой шторкой спрятаны изображения детей, с помощью маркера их легко переместить в точку пересечения биссектрис).

По окончании этой истории учащиеся записывают в тетрадях выводы:

1) точка, лежащая на биссектрисе угла, равноудалена от его сторон; 2) точка, равноудаленная от сторон треугольника, является точкой пересечения биссектрис его углов.

Данные выводы учащиеся делают из наглядно-образных представлений и основываясь на знаниях о свойствах геометрических фигур, усвоенных ими к данному периоду обучения. Такая пропедевтика на данном этапе изучения геометрического материала оказывается полезной.

5. Этап первичного закрепления знаний.

Учащимся предлагается еще раз проверить факт пересечения всех трех биссектрис треугольника в одной точке, рассмотрев различные виды треугольников: 1 вариант – в тупоугольном, 2 вариант – в прямоугольном.

6. Итог урока и домашнее задание

Учащиеся отвечают на вопросы, демонстрируемые на интерактивной доске, записывают домашнее задание (ресурс «Геометрические фигуры», страница 12). Учитель подводит итоги урока, объявляет все оценки, выставленные учащимся за урок.

Проводится рефлексия психологического состояния и эмоционального восприятия урока (ресурс «Геометрические фигуры», страница 13).