
Тема: Корни и степени. Корни натуральной степени из числа их свойства.
Цель урока: повторить и систематизировать знания учащихся о квадратном корне; сформировать у учащихся понятие корня степени n.Формировать умение учащихся работать с корнями четной и нечетной степеней.
Степени
Определим понятие степени, показатель которой — натуральное число (т.е. целое и положительное).
1.
По
определению: ![]() .
.
2.
Возвести
число в квадрат — значит умножить его само на себя: ![]()
3.
Возвести
число в куб — значит умножить его само на себя три раза: ![]() .
.
Возвести число в натуральную степень ![]() — значит
умножить число само на себя
— значит
умножить число само на себя ![]() раз:
раз:
![]()
Степень с целым показателем {0, ±1, ±2,...}
Если показателем степени является целое положительное число:
![]() , n > 0
, n > 0
Возведение в нулевую степень:
![]() , a ≠ 0
, a ≠ 0
Если показателем степени является целое отрицательное число:
![]() , a ≠ 0
, a ≠ 0
Примечание:
выражение ![]() не
определено, в случае n ≤ 0. Если n > 0, то
не
определено, в случае n ≤ 0. Если n > 0, то ![]()
Пример 1.
![]()
Степень с рациональным показателем
Если:
§ a > 0;
§ n — натуральное число;
§ m — целое число;
Тогда:
![]()
Пример 2.
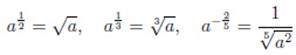
Свойства степеней
|
Произведение степеней |
|
|
Деление степеней |
|
|
Возведение степени в степень |
|
Пример 3.
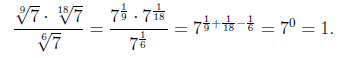
Примеры для решения у доски:
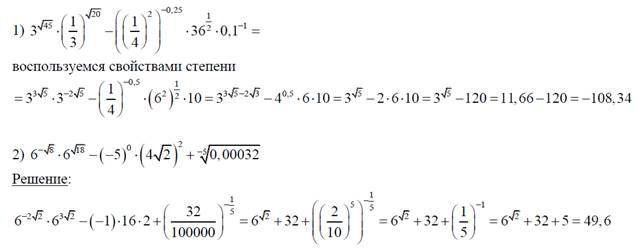
Корни
С понятием квадратного корня из числа а вы уже знакомы: это такое число, квадрат которого равен а.
![]() ,
,
![]() ,
,
![]() ,
, ![]()
Аналогично определяется
корень ![]() -й
степени из числа а, где
-й
степени из числа а, где![]() –
произвольное натуральное число.
–
произвольное натуральное число.
А теперь давайте решим такое уравнение:
![]()
Итак, это уравнение мы можем переписать в таком
виде: ![]() .
Или
.
Или ![]() .
.
Тогда наше уравнение равносильно совокупности
уравнений: ![]() .
.
Понятно, что уравнение ![]() не
имеет решения на множестве действительных чисел. Значит, остаётся решить
уравнение
не
имеет решения на множестве действительных чисел. Значит, остаётся решить
уравнение
![]()
![]()
![]()
![]()
![]()
![]()
Итак, наше уравнение ![]() имеет
два действительных корня 5 и –5. Их называют корнями четвёртой
степени из числа 625. В свою очередь, положительный корень (число
5) называют арифметическим корнем четвёртой степени из
числа 625. Обозначают его так:
имеет
два действительных корня 5 и –5. Их называют корнями четвёртой
степени из числа 625. В свою очередь, положительный корень (число
5) называют арифметическим корнем четвёртой степени из
числа 625. Обозначают его так: ![]() .
Таким образом,
.
Таким образом, ![]() .
.
Запомните!
Арифметическим корнем натуральной степени ![]() из
неотрицательного числа а называется неотрицательное
число,
из
неотрицательного числа а называется неотрицательное
число, ![]() -я
степень которого равна а.
-я
степень которого равна а.
Арифметический корень ![]() -ой
степени из числа а обозначают так:
-ой
степени из числа а обозначают так: ![]() .
Символ
.
Символ ![]() называют знаком
арифметического квадратного корня или радикалом (от
латинского слова «радикс» – корень), число
называют знаком
арифметического квадратного корня или радикалом (от
латинского слова «радикс» – корень), число ![]() называется показателем корня,
а число а, стоящее под знаком корня, – подкоренным
выражением.
называется показателем корня,
а число а, стоящее под знаком корня, – подкоренным
выражением.
Вам хорошо известен такой
частный случай арифметического корня ![]() -й
степени, как корень второй степени, или квадратный корень из
числа, то есть когда
-й
степени, как корень второй степени, или квадратный корень из
числа, то есть когда ![]()
В этом случае показатель корня не пишут, а пишут
просто![]() .
.
Ещё одним частным случаем
является![]()
![]() мы
привыкли называть его корнем кубическим.
мы
привыкли называть его корнем кубическим.
Как правило, когда ясно, что
речь идёт об арифметическом корне ![]() -й
степени, слово «арифметический» не произносят, а говорят кратко: «корень
энной степени».
-й
степени, слово «арифметический» не произносят, а говорят кратко: «корень
энной степени».
Действие, посредством которого
отыскивается корень ![]() -й
степени, называется извлечением корня
-й
степени, называется извлечением корня ![]() -й степени.
Это действие является обратным действию возведения в
-й степени.
Это действие является обратным действию возведения в ![]() -й
степень.
-й
степень.
Равенство ![]() при
при ![]() верно,
когда выполняются два условия:
верно,
когда выполняются два условия:![]() ;
второе —
;
второе —![]() .
.
Например,![]() .
.
Число![]() ;
;
![]() .
.
Видим, что оба условия выполняются. Значит![]() верно.
верно.
Из определения арифметического корня следует, что если![]() ,
то
,
то![]() .
.
Например,![]()
![]()
А теперь давайте решим следующие уравнения: ![]() и
и ![]() .
Итак, первое уравнение
.
Итак, первое уравнение
![]()
Перепишем это уравнение в виде: ![]() .
.
Преобразуем наше уравнение, применяя формулу разности
кубов. Имеем:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Перейдём к уравнению 2:
![]()
Перепишем это уравнение в виде: ![]() .
.
Преобразуем наше уравнение, применяя формулу разности
кубов. Имеем:![]() .
.
![]()
![]()
![]()
![]()
Так как ![]() ,
то число –4 является корнем из числа –64. Однако это число не является
арифметическим корнем по определению. Число
,
то число –4 является корнем из числа –64. Однако это число не является
арифметическим корнем по определению. Число ![]() называют
корнем кубическим из числа
называют
корнем кубическим из числа ![]() и
обозначают так:
и
обозначают так:![]()
Вообще, для любого нечётного натурального числа![]() ,
уравнение
,
уравнение![]() ,
при
,
при ![]() имеет
только один корень, причём отрицательный. Этот корень обозначается, как и
арифметический корень, символом
имеет
только один корень, причём отрицательный. Этот корень обозначается, как и
арифметический корень, символом![]() .
.
И называют его корнем нечётной степени из отрицательного числа.
Запомните! При нечётном ![]() существует
существует![]() ,
и притом только один. Для корней нечётной степени справедливо равенство
,
и притом только один. Для корней нечётной степени справедливо равенство ![]()
Например,
![]()
![]()
Корень нечётной степени из отрицательного числа а
связан с арифметическим корнем из числа ![]() следующим
равенством:
следующим
равенством:![]()
Например, ![]()
Арифметический корень ![]() -й
степени обладает несколькими свойствами. Перечислим их. Итак, при условии, что
-й
степени обладает несколькими свойствами. Перечислим их. Итак, при условии, что![]() ,
, ![]() ,
а
,
а![]() ,
, ![]() и
и ![]() –
натуральные числа, причём
–
натуральные числа, причём![]() ,
, ![]() ,
справедливы равенства:
,
справедливы равенства:
1. Корень n-степени (n=2,3,4,5, …) из произведения неотрицательных чисел равен произведению корней n-степени из этих чисел:
![]() .
.
2. Чтобы извлечь корень из дроби, нужно извлечь корень из числителя и знаменателя отдельно и первый результат разделить на второй
![]() .
.
3. Если a≥0, n=2,3,4,5,… и m – любое натуральное число, то справедливо равенство:
![]() .
.
4. Если a≥0, n и
k - натуральные числа, большие 1, то справедливо равенство: ![]() .
.
5. Если показатели
корня и подкоренного выражения умножить или разделить на одно и то же отличное
от нуля число, то значение корня не изменится: ![]() .
.
Обратите внимание, что в первом свойстве число ![]() может
также быть равным
может
также быть равным ![]() ;
в третьем свойстве число
;
в третьем свойстве число ![]() может
быть любым целым, если
может
быть любым целым, если ![]() .
.
Докажем справедливость этих свойств. Итак, первое свойство.
1. ![]() .
.
По определению арифметического корня ![]() –
это такое неотрицательное число,
–
это такое неотрицательное число, ![]() -я
степень которого равна произведению
-я
степень которого равна произведению ![]() .
.
![]() ;
;
![]() .
.
![]()
2. ![]() .
.
![]() ;
;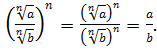
3. ![]() .
.
![]() ;
;
![]() .
.
4. ![]() .
.
![]() ;
;
![]() .
.
5. ![]() .
.
![]() ;
;
![]() .
.
А теперь давайте приступим к практической части нашего урока.
Задание 1.
Найдите значения выражений
а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() .
.
Решение.
а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() .
.
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
Задание 2.
Преобразуйте выражения:
а) ![]() ;
б)
;
б) ![]() ;
в)
;
в) ![]() ;
г)
;
г) ![]() .
.
Решение.
а) ![]() ;
;
б) ![]()
![]()
![]() ;
;
в) ![]() ;
;
г) ![]() .
.
Примеры для самостоятельного решения:
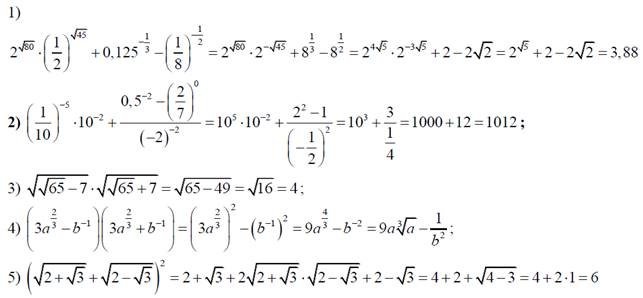
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.