
КГУ «Индустриально-технологический колледж»
Поурочный план № 153-154
Куб и ее элементы. Площадь боковой и полной поверхности куба.
(тема занятия)
Наименование
дисциплины: Математика
Подготовил педагог: Тихоненко С.А.
Дата урока: 28.04.2021 года
1. Общие сведения
1.1 Курс, группы: первый, 9СЛ20, 9МК20, 9ОП20
1.2 Тип занятия: комбинированный/ дистанционный
1.3 Межпредметные связи: физика, черчение.
2. Цели, задачи:
Цели урока:
познакомить с элементами куба; познакомить с новыми понятиями, связанными с кубом.
Задачи урока:
научить чертить куб, учить находить площадь поверхности куба, применять полученные знания в жизни.
2.2 Результаты обучения:
1) Усвоить понятие многогранник.
2) Решать задачи на нахождение элементов многогранников, площади поверхности.
2.3 Критерии оценки:
1) Раскрывает содержание понятия многогранника и его элементов;
2) Объясняет свойства многогранников по видам.
3) Изображает многогранники и выполняет их развёртки;
4) Определяет виды правильных многогранников;
5) Решает задачи на нахождение элементов многогранников;
6) Применяет формулы площади боковой и полной поверхности многогранников при решении задач.
3. Оснащение занятия
3.1 Учебно-методическое оснащение: дидактические материалы, справочно-инструктивные таблицы, карточки с заданиями, оценочные листы.
Справочная литература: А.Е.Әбылқасымова, В.Е. Корчевский, З.Ә. Жумагулова, Алгебра и начала анализа: Учебник для 10 классов естественно- математического направления обшеобразовательных школ.1-2 часть. Алматы: Мектеп, 2019г.
3.2 Техническое оснащение, материалы, ИКТ: мультимедийный проектор, ноутбук, экран.
4. Ход занятия
|
Заплани- рованные этапы урока, время |
Деятельность, запланированная на уроке
|
Ресурсы
|
|
Начало урока |
Орг. момент. |
|
|
|
Проверка домашнего задания. Повторение. · Что называют пп? · Виды пп. · Расскажите алгоритм построения пп.
|
Презентация
|
|
Середина урока |
https://drive.google.com/file/d/1SpAuXqH38NmLBI6T8KP_uBqVQhuR2PID/view?usp=sharing
http://school-collection.edu.ru/catalog/res/3208b518-f002-4c6a-a8ce-210e81e71261/view/
Куб – это такой прямоугольный параллелепипед, в котором все рёбра равны между собой. Обратите внимание, что рёбра куба, которые не видны, мы изображаем пунктирными линиями. Это позволяет получить полное представление о фигуре и её расположении по отношению к нам.
Все грани куба – равные между собой квадраты. Поверхность куба состоит из 6 равных квадратов. Посмотрите, что грани, расположенные друг против друга, не имеют общих рёбер. Эти грани называются противоположными. Грани, которые имеют общее ребро, называются смежными. А теперь давайте проведём небольшой эксперимент. Возьмём коробку, которая имеет форму куба. Откроем её, потом разрежем по четырём вертикальным рёбрам, а затем развернём.
Фигуру, которая у нас получилась, называют развёрткой куба. Она состоит из 6 равных квадратов.
Следующие фигуры также являются развёртками куба.
С помощью любой из развёрток вы можете изготовить модель куба. Для этого можно поступить следующим образом. Начертить на листе бумаги развёртку куба. Вырезать её. Согнуть по отрезкам, которые соответствуют рёбрам куба, и склеить. Теперь давайте проведём с вами отрезок, который соединит наиболее удалённые друг от друга вершины куба. Эти вершины называют противоположными. Отрезок, соединяющий две противоположные вершины куба, называется диагональю куба.
Формулы для куба Примем следующие обозначения, которые будут использоваться далее: · a – ребро куба; · d – диагональ куба или его грани. Диагональ Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.
Диагональ грани Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.
Площадь полной поверхности Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.
Периметр ребер Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.
Объем Объем куба равен длине его ребра, возведенной в куб.
Радиус описанного вокруг шара Радиус шара, описанного около куба, равняется половине его диагонали.
Радиус вписанного шара Радиус вписанного в куб шара равен половине длины его ребра.
|
Ссылка 1, 2 Презентация к уроку. |
|
|
Закрепление. Задача первая. Определите, какой кубик получится из данной развёртки.
Решение. Давайте мысленно представим, какие грани кубика являются смежными, то есть имеют общее ребро, и сравним с предложенными вариантами, чтобы найти верный. Для этого нам удобнее всего сравнивать грани, которые отличаются по нанесённому на них рисунку. Обратите внимание на грань с жёлтым треугольником и грань с зелёным треугольником. Очевидно, что эти грани будут смежными при сборке кубика. При этом возможны четыре варианта взаимного расположения этих граней при различных поворотах кубика. Теперь сравним с четырьмя предложенными вариантами. Сразу видим, что вариант первый неверный. Вариант второй неверный. Очевидно, что вариант третий тоже неверный. А вот вариант четвёртый верный, так как грани, на которых изображены треугольники, расположены верно. При этом на верхней грани должен быть изображён синий круг. Действительно так. Таким образом, мы с вами выяснили, что из данной развёртки получится куб под номером 4. Задача вторая. Модель куба с длиной ребра 4 сантиметра окрасили в серую краску и распилили вдоль рёбер на кубики с длиной ребра 1 см. Сколько среди полученных кубиков: а) окрашенных с трёх сторон; б) окрашенных с двух сторон? Решение.
|
Презентация
|
|
Конец урока |
Рефлексия |
Слайд |
|
|
Домашнее задание: 1. Написать конспект. 2. Решить задачи. |
Карточка-задание |
5.Рефлексия по занятию
Рефлексия «+, -, интересно».
- Понравился ли вам урок?
- Что было трудным для вас?
- Что вам больше понравилось?
6. Домашнее задание
Оценочный лист:
|
№ |
Выполненное задание: |
Баллы |
|
1. |
Составить конспект. |
30 |
|
2. |
Решить задачи. |
70 |
Задача 3. На рисунке изображён каркас куба. Проведите видимые рёбра так, чтобы куб был «виден»: а) сверху слева; б) снизу справа. Выполните построения в тетради.
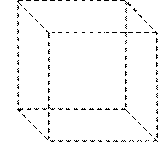
Задача 4. На рисунке изображена фигура, сложенная из пяти кубиков. Какой вид будет иметь данная фигура, если смотреть на неё: а) спереди; б) слева; в) сверху? Изобразить в тетради в цвете.

Задача 5. Найти полную поверхность и объём куба со стороной 10 см.
Задача 6. Диагональ куба 27 м. Найти боковую и полную поверхность куба.
Подпись преподавателя________________________
Скачано с www.znanio.ru
Материалы на данной страницы взяты из открытых источников либо размещены пользователем в соответствии с договором-офертой сайта. Вы можете сообщить о нарушении.