Конспект урока на тему "Правила дифференцирования"

Правила дифференцирования

Тип урока: 

·         по способу проведения - урок-практикум;

·         по дидактической цели – урок ознакомления с новым материалом.

Цель: вспомнить формулы нахождения производных вида x^p, формировать умения находить производные суммы, произведения, частного.

Задачи:

Образовательные: изучить правила дифференцирования; сформировать у учащихся умения решать задачи по данной теме; применять данные правила на практике.

Развивающие: развивать логическое мышление, память, внимание, сопоставлять данные, выводить логические следствия из данных предпосылок, умение делать выводы.

Воспитательные: воспитывать нравственные качества личности, аккуратность, добросовестное отношения к работе.

Методы работы:

·         словесный;

·         наглядный;

·         практический.

 Оборудование урока: интерактивная доска или проектор.

Структура урока: 

1.     Организационный момент. 1 минута

2.     Постановка цели и задач урока. Мотивация учебной деятельности учащихся.  минут. 1минута

3.     Актуализация знаний. 13 минут

4.     Закрепление изученного материала. 17 минут

5.     Повторение. 4 минуты

6.     Рефлексия учебной деятельности на уроке. 3 минуты

7.     Информация о домашнем задании. 1 минута

              Ход урока

1.     Организационный момент 

Приветствие учителем класса, проверка готовности кабинета и учащихся к уроку.

2.      Постановка цели и задач урока и мотивация учебной деятельности учащихся.

3.     Язык математики межпредметный, межнаучный.  Всем наукам приходится

4.     сталкиваться с зависимостями друг от друга значений величин. Математика как «верная

5.     помощница» всех наук должна уметь «переводить» зависимости на свой язык.

6.     Язык математики межпредметный, межнаучный.  Всем наукам приходится

7.     сталкиваться с зависимостями друг от друга значений величин. Математика как «верная

8.     помощница» всех наук должна уметь «переводить» зависимости на свой язык.

9.     Язык математики межпредметный, межнаучный.  Всем наукам приходится

10. сталкиваться с зависимостями друг от друга значений величин. Математика как «верная

11. помощница» всех наук должна уметь «переводить» зависимости на свой язык.

Учитель: Ребята мы научились с вами находить производные степенных функций вида и линейной функции вида . Но у нас вызовет затруднения, если необходимо найти сумму, произведение, частное этих функций.  Поэтому тема нашего урока….?

2.     Актуализация знаний

Учитель: На сегодняшнем уроке мы приступаем к изучению новой темы «Правила дифференцирования». Мы изучим с вами правила дифференцирования суммы, произведения и частного двух функций и вынесение постоянного множителя за знак производной. Научимся решать задачи.

Перед изучением новой темы производится устный счет. На интерактивном экране написаны примеры и ученикам необходимо найти их производные:

Правило 1: Производная суммы.

А теперь давайте попробуем найти производную функции f’(x) =  Для того чтобы выполнить это задание необходимо знать правило нахождения производной двух функций: производная суммы равна сумме производных этих функций

Пример 1: .

Чтобы найти производную суммы нескольких функций необходимо найти сумму производных от каждой из этих функций.

Пример 2: .

Правило 2: Вынесение постоянного множителя за знак производной.

Постоянный множитель можно вынести за знак производной.

.

Пример 3: .

Правило 3: Производная произведения.

.

Пример 4: .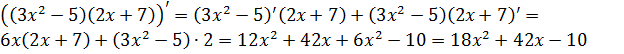

Правило 4: Производная частного.

.

Пример 5: =

12. Во всех этих выражениях мы указали формулу, позволяющую для каждого

13. значения одной переменной однозначно вычислить значение другой переменной.

4.     Закрепление изученного материала.

Решение номеров №802(чётные), 803(чётные), 810(чётные).

Предложение учащимся провести самооценку своих работ, сравнить ответы по тетрадям, рабочим листам и образцам на доске.

Разъяснения по возникающим вопросам решения или самооценки.

5.      Повторение.

 Решение №805

6.     Рефлексия учебной деятельности на уроке.

Учащимся необходимо ответить на вопросы.

1.     Как найти производную от суммы нескольких функций?

2.     Как найти производную произведения двух функций?

3.     Чему равно производная частного?

4.     Какие вопросы у вас остались?

7.      Информация о домашнем задании.

   Выучить правила, №802(нечётные), 803(нечётные), 810(нечётные).